转子磁极分段移位斜极对永磁同步电机转矩的影响

胡启国， 吴明钦

( 重庆交通大学 机电与车辆工程学院， 重庆 400074 )

永磁同步电动机以高效、高转矩密度、低振动噪声的性能特点而被广泛应用于工业运用之中[1].但永磁电机中存在较多谐波影响着其性能，因此有针对性地削弱谐波能够改善电机的性能.电机产生的振动和噪声等一系列负面影响的根源是齿槽转矩及转矩脉动，国内外学者对此提出了许多削弱或抑制的方法.Lin等[2]、Chen等[3]和鲍晓华等[4]基于能量法，对永磁体进行重新设计达到抑制齿槽转矩，但是需要重新对电机气隙磁密和永磁体用量进行优化，较为繁琐.郭有权等[5]和Ge等[6]在不同类型的电机上采用磁极偏移法对齿槽转矩进行削弱，但需要重新设计转子并会引入新的谐波.杨金歌等[7]和Bianchi等[8]通过开辅助槽法抑制齿槽转矩，但未全面解析辅助槽的各个参数.郑蓉蓉等[9]通过定子齿偏移法，提高输出转矩并降低了转矩脉动，然而定子齿偏移会造成绕组设计困难.

本文以8极48槽内置永磁同步电机作为样机，分析和验证轴向单方向转子磁极分段移位斜极方法，并在转子不同分段数情况下，对齿槽转矩谐波抑制，以及对负载转矩及转矩脉动进行分析验证.

1 转子分段移位斜极方法

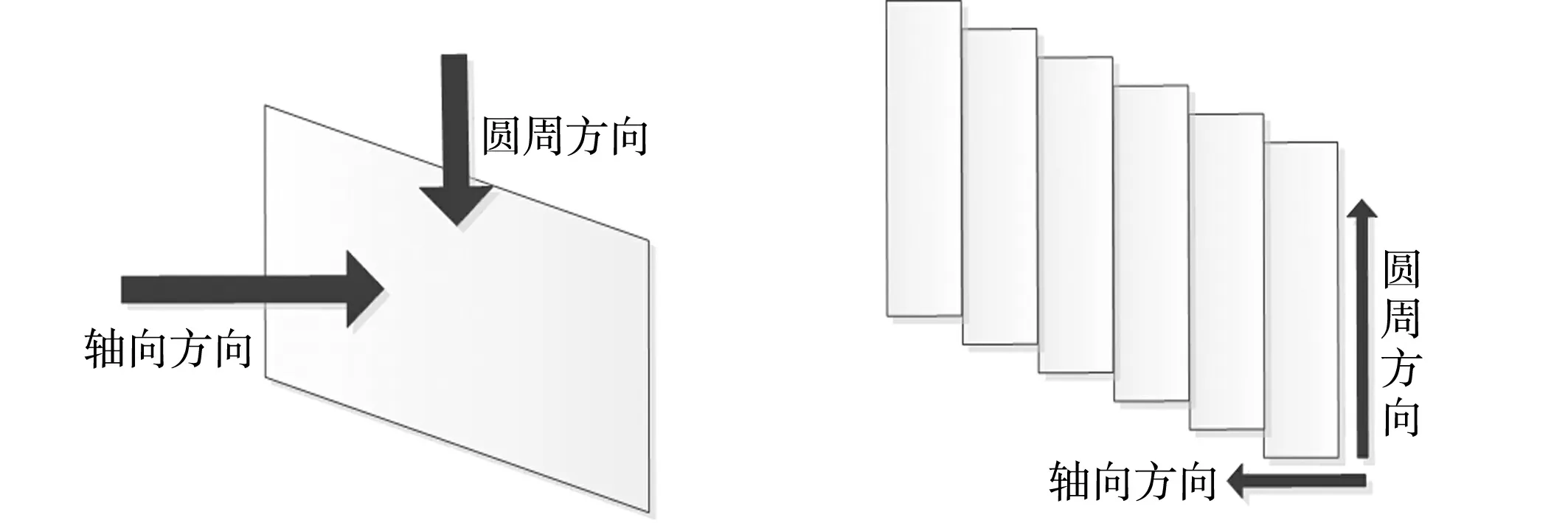
(a) 转子磁极连续斜极 (b) 转子磁极分段移位斜极图1 两种常用的转子斜极方式Fig.1 Two commonly used rotor oblique pole methods

常见的转子斜极有两种方式[10-11]，一种是转子磁极连续斜极，另一种是转子磁极分段移位斜极，如图1所示.转子斜极在实际应用上存在装配工艺困难等问题.所以，为了更好地解决工艺问题，采取转子磁极分段移位斜极的方法，并且采用此方法能够有效地减小磁钢的涡流损耗、降低磁钢温度，以及提高永磁体抗去磁能力.

转子斜极与定子斜槽削弱谐波的基本原理是一致的.根据斜槽系数的求解，可以得到相对应的转子磁极分段移位斜极的第v次谐波对应的分段移位斜极系数kmagnet_section_v[12]为

(1)

式(1)中：p为电机的极对数；θr为转子偏移的机械角度；n为转子磁极轴向分段数.

采用定子斜槽或转子磁极分段移位斜极，其斜极移位角为此谐波的半个周期角来削弱此阶齿谐波，而转子磁极分段移位斜极角可由式(1)推导计算得到，即

kmagnet_section_v=0.

(2)

由此可得转子磁极分段移位斜极的机械角度[13]为

(3)

式(1)中：LCM(Zs，2p)为定子槽数和极数的最小公倍数.

定子斜槽机械角度[14]计算式为

(4)

由此可见，转子轴向移位分段数越多就越接近定子斜槽的角度，也就说明转子磁极分段数较多时，达到的效果和定子斜槽基本相同.然而，分段数不仅受到轴向长度的制约，而且随着分段数的增加，必然会增加加工艺的复杂.所以，需要结合实际有针对性的选择一个较为合适的转子磁极分段数来削弱相对应的齿谐波.

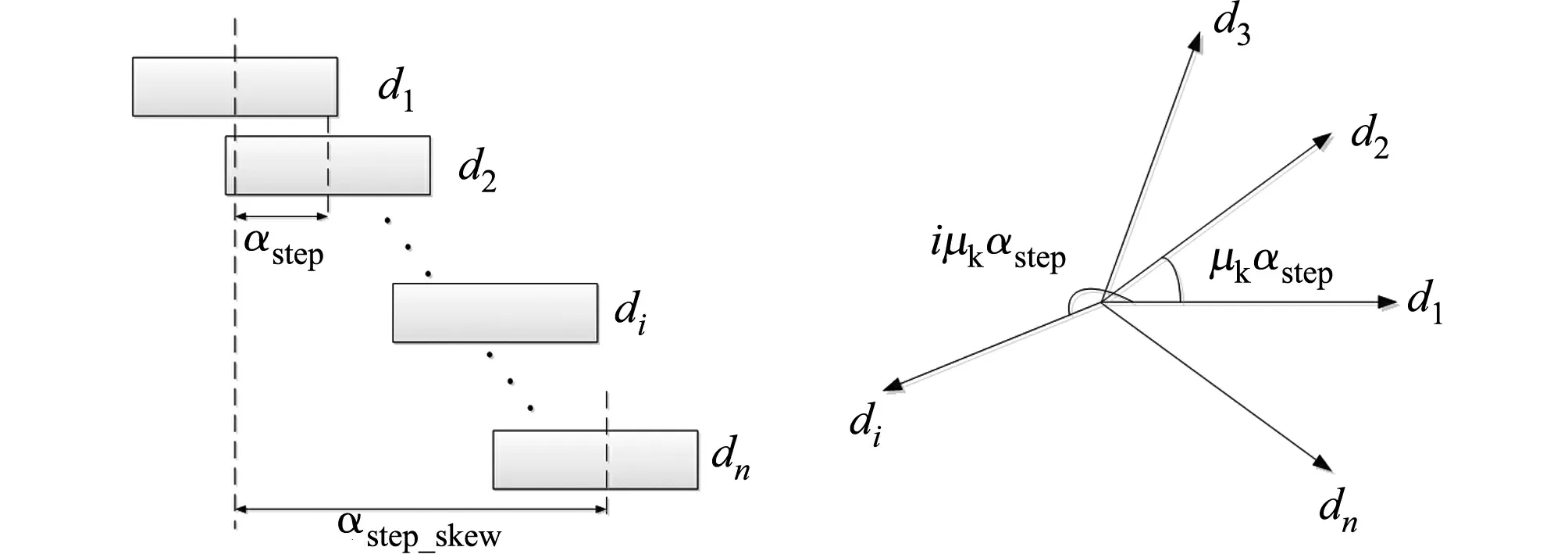
图2 转子单方向分段移位斜极及矢量图Fig.2 Oblique pole and vector diagram of single-direction piecewise shift of rotor

从矢量合成分析转子磁极分段移位斜极角度，在采用针对性的削弱谐波方法时，需要将转子平均分成n段，以削弱k阶齿谐波产生的齿槽转矩.那么根据矢量合成，应使由n个矢量迭加的第μk次(k·LCM(Zs，2p)/p)齿槽转矩谐波抵消为0.

转子单方向分段移位斜极及矢量图形分布，如图2所示.图2中：αstep为相邻两段磁钢之间的电角度；αstep_skew为总的磁钢偏移电角度.

根据矢量合成，第μk次齿槽转矩谐波的n个矢量迭加和为0[15]，即

(5)

由此可得出转子相邻两段之间的转子移位电角度，以及转子总移位电角度分别为

(6)

式(6)的计算结果与式(3)相同.文中主要考虑的是削弱一阶齿谐波.如果需要削弱其他阶齿谐波，可通过上式分析得相应的转子磁极不同分段数的移位角.每种结构总的轴向长度相同，且每种结构中的各段轴向长度都分别相等.转子轴向1～6段转子结构图，如图3所示.

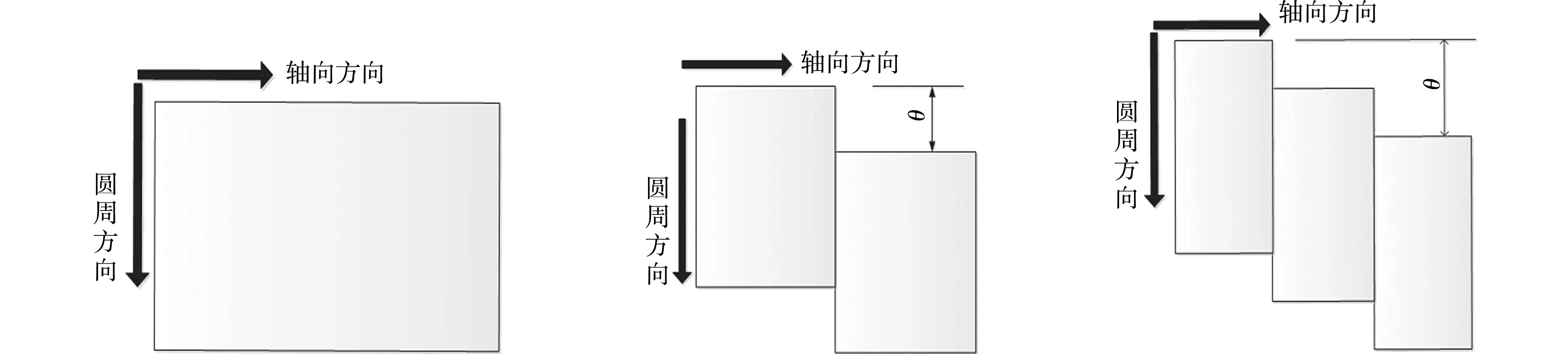
(a) 不分段 (b) 分两段 (c) 分三段

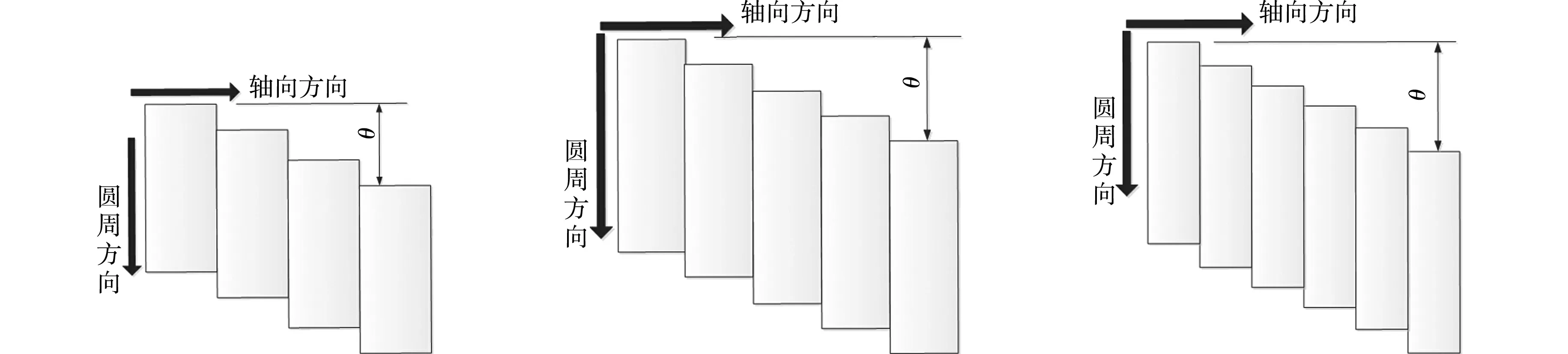
(d) 分四段 (e) 分五段 (f) 分六段图3 转子磁极不同分段移位斜极图Fig.3 Skew diagram of rotor magnetic pole shift in different segments

2 转子磁极分段移位斜极的转矩分析

2.1 电机建模及转矩理论分析

试验的分析样机为一台8极48槽的电动汽车驱动用内置式永磁同步电机，电机相关参数如表1所示.表1中：P为额定功率；v为转速；Zs，p分别为极数和槽数；Ds为定子外径；Dr为转子外径.

表1 电机相关参数Tab.1 Motor related parameters

使用Ansoft Maxwell软件建立电机模型，由于8极48槽电机属于整数槽电机，也为了缩短仿真时间，使用1/4的Maxwell 2D模型，进行二维场仿真分析.电机的1/4有限元模型，如图4所示.

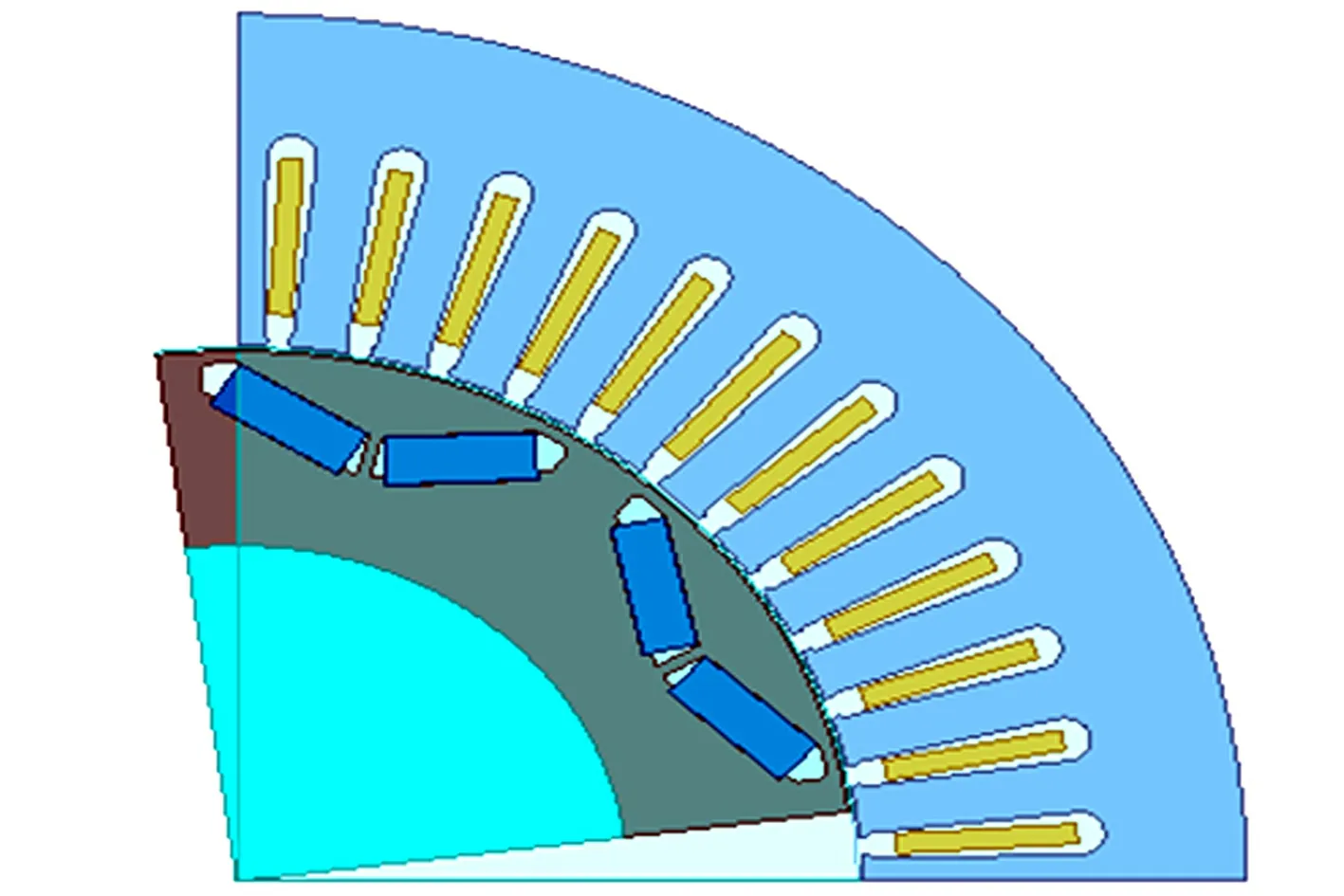
图4 电机有限元模型Fig.4 Motor finite element model

根据式(4)计算得到转子磁极分段数与相应的分段移位斜极角关系，如表2所示.表2中：n为转子磁极分段数；θr为分段移位斜极机械角度.

表2 电机转子磁极分段数与分段移位斜极角的关系Tab.2 Relation between number of segments of rotor pole and segment shift oblique pole angle

根据三角函数迭加的性质，结合式(5)，(6)，第vμk次齿槽转矩谐波(v为1，2，3，…)具有性质为

(7)

从式(7)可以看出，在一个电周期内，转子磁极分段移位斜极角削弱第k阶齿槽转矩的各阶削弱情况.当v不是n的整数倍时，v·μk次齿槽转矩谐波都得到削弱；当v是n的整数倍时，v·μk次齿槽转矩谐波没有得到削弱.电机的齿槽转矩谐波削弱次数与转子磁极分段数的关系，如表3所示.表2中：n为转子磁极分段数；v为齿槽转矩谐波次数；“0”表示可以完全抵消，“≠0”表示不能抵消或者削弱.

表3 齿槽转矩谐波削弱次数与分段数的关系Tab.3 Relationship between harmonic attenuation times and number of segments

由表3可知:当转子磁极分n段削弱第k阶齿槽转矩谐波时，第n·k的整数倍阶齿槽转矩无法得到削弱.若转子磁极分2段以削弱1阶齿槽转矩，第2，4，6，8，…阶齿槽转矩谐波无法得到削弱；若转子磁极分3段以削弱1阶齿槽转矩，第3，6，9，12，…阶齿槽转矩谐波无法得到削弱；若转子磁极分2段以削弱3阶齿槽转矩，第6，12，18，24，…阶齿槽转矩谐波无法得到削弱；若转子磁极分3段以削弱2阶齿槽转矩，第6，12，18，24，…阶齿槽转矩谐波无法得到削弱；若转子磁极分2段以削弱3阶齿槽转矩，第6，12，18，24，…阶齿槽转矩谐波无法得到削弱；若转子磁极分3段以削弱2阶齿槽转矩，第6，12，18，24，…阶齿槽转矩谐波无法得到削弱.

式(7)分析的是μk的整数倍次齿槽转矩.当μk为二阶及以上齿槽转矩时，会存在μk的非整数倍次齿槽转矩(j=1，2，…，k-1).低于μk的谐波关系表达式为

(8)

根据式(8)可以发现：μk的非整数倍次齿槽转矩次数都存在，都得到一定程度的削弱.由此可得，当转子磁极分n段时，非n的最小公倍数阶齿槽转矩谐波得到削弱.

2.2 齿槽转矩仿真分析

永磁电机绕组不通电的情况下，永磁体和定子铁心的齿槽相互作用在圆周方向上产生的转矩称为齿槽转矩[16].其本质是永磁体与电枢齿之间相互作用力的切向分量引起的.齿槽转矩是永磁电机特有的问题之一，特别是整数槽的内置式永磁同步电机较为明显.根据表2转子不同分段数的移位斜极角得到转子磁极不同移位分段数的齿槽转矩波形，如图5所示.

对每个分段数的齿槽转矩进行Fourier分解，可得到齿槽转矩的各阶齿槽转矩谐波分量，如表4所示.表4中：n为转子磁极分段数；Ti为各齿槽转矩峰值；峰-峰值表示周期内齿槽转矩的波动值；η为优化百分比；“≈0”表示数据值接近于零.

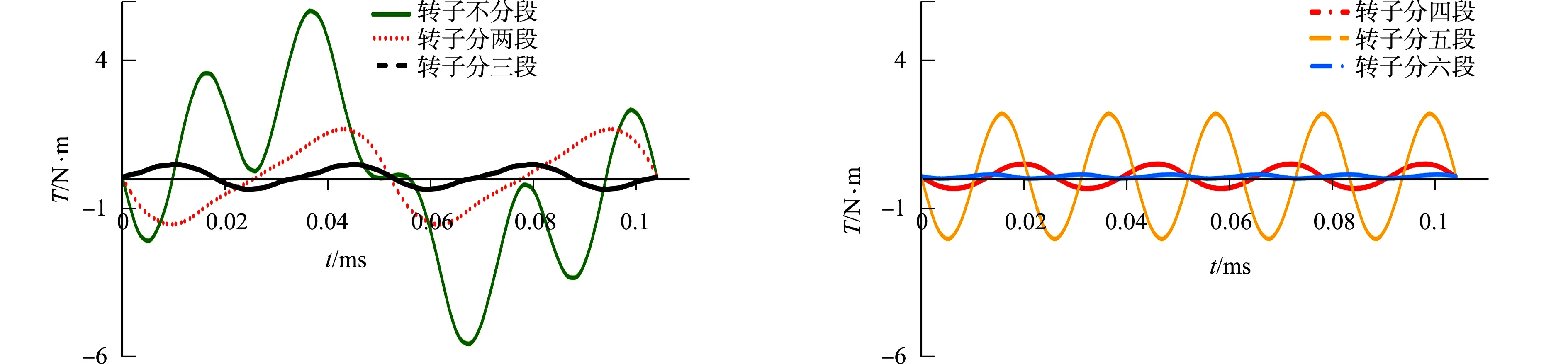
(a) 转子磁极不分段至三段 (b) 转子磁极分四段至六段图5 转子磁极不同分段数形成的齿槽转矩波形Fig.5 Rotor magnetic pole torque waveform with different number of segments

表4 齿槽转矩的各次谐波分量Tab.4 Harmonic components of cogging torque

从图5(a)可知：当转子磁极不分段时，齿槽转矩幅值较大且波动较大，振动较为明显，谐波较为丰富，齿槽转矩的峰-峰值为11.28 N·m；而当转子磁极分两段时，齿槽转矩周期较为明显，转矩幅值下降也较为明显，与转子磁极不分段相比转矩的峰-峰值下降为3.22 N·m，削弱了71.5%.从表4可知：转子磁极分两段时，1，3，5阶齿槽转矩谐波得到了明显的削弱，而2，4，6阶齿槽转矩谐波没有得到削弱，二倍数阶齿槽转矩谐波为转子磁极分两段的主要分量.

从图5(a)还可知：当转子磁极分三段时，齿槽转矩周期较为明显，与转子磁极不分段和转子磁极分两段的转矩相比也有较明显的降低，齿槽转矩的峰-峰值下降为0.85 N·m，削弱了92.5%.从表4也可知：转子磁极分三段时，1，2，4，5阶齿槽转矩谐波得到明显削弱，3，6阶谐波没有得到削弱，三倍数阶齿槽转矩谐波为转子磁极分三段的主要分量.

从图5(b)可知：当转子磁极分四段时，齿槽转矩周期较为明显，与转子磁极不分段和转子磁极分两段的转矩相比有较明显的降低，但与转子磁极分三段相比没明显变化，齿槽转矩的峰-峰值为0.82 N·m，削弱了92.7%.从表4可知，当转子磁极分四段时，1，2，3，5，6阶齿槽转矩谐波得到明显削弱，4阶谐波没有得到削弱，四倍数阶齿槽转矩谐波为转子磁极分四段的主要分量.

从图5(b)还可知：当转子磁极分五段时，齿槽转矩周期较为明显，与转子磁极分段数为2～4相比，齿槽转矩明显较大，只比转子磁极不分段略小，齿槽转矩的峰-峰值下降为4.25 N·m，削弱了62.3%.从表4还可知：当转子磁极分五段时，1，2，3，4，6阶齿槽转矩谐波得到明显削弱，5阶谐波没有得到削弱，五倍数阶齿槽转矩谐波为转子磁极分五段的主要分量.

从图5(b)还可知：当转子磁极分六段时，六阶齿槽转矩周期较为明显，齿槽转矩的峰-峰值为0.14 N·m，削弱了98.6%.从表4还可知：当转子磁极分六段时，1，2，3，4，5阶齿槽转矩谐波得到明显削弱，6阶谐波没有得到削弱，六倍数阶齿槽转矩谐波为转子磁极分六段的主要分量.

通过对转子磁极不同分段数形成的齿槽转矩分析，随着分段数的逐渐增加，齿槽转矩有明显的下降.但是，其齿槽转矩波动趋于相同，并且可以得到当转子分n段时，第n及n的倍数阶齿槽转矩谐波削弱较为不明显，其余各阶谐波削弱较为明显与式(7)推导结论相符.

2.3 负载转矩分析

对于电机的各个性能中，输出转矩最为重要.输出转矩平均值直接体现电机输出大小，直接影响电机所能够带动的负载，同时体现电机的转矩密度.输出转矩的脉动直接体现出电机的品质，影响电机的运行.转矩脉动是由齿槽转矩和由定子相电流与相反电势相互作用，产生的平均转矩和纹波转矩共同作用形成.对样机进行峰值负载运行仿真分析，转矩仿真数据如表5所示.表5中：n为转子磁极分段数；Tav为平均转矩；Tmax为最大转矩；Tmin为最小转矩；FTR为转矩脉动.

表5 转矩的仿真数据Tab.5 Torque simulation data

从表5可知：转矩脉动主要是电枢反应导致气隙磁场畸变而引起的，这使得主磁场也有一定的削弱，造成输出转矩的减少.此外，平均转矩、最大转矩都随着转子磁极分段数的增加逐渐降低，而最小转矩随着分段数的增加略有提高；转子磁极分两段时，其变化较为明显，平均转矩、最大转矩分别下降了5.33，18.81 N·m；而最小转矩增加9.88 N·m，并随着转子磁极分段数再次增加而趋于平稳，与基波削弱系数规律基本相同.

从表5还可知：转子磁极变化趋势与电磁转矩相同，随着转子磁极分段数的增加逐渐降低，然后趋于稳定；转子磁极分两段时尤为明显且降低为5.56%，与转子磁极不分段相比下降60%.

样机有限元仿真采用理想三相对称的正弦波电流，当转子磁极采用轴向分段时，此时齿槽转矩不是造成转矩脉动的主要因素.转子磁极不同分段的转矩性能，如图6所示.

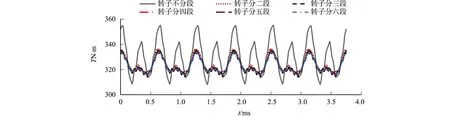
图6 转子磁极不同分段数下的电磁转矩波形Fig.6 Electromagnetic torque waveforms under different segment numbers of rotor poles

从图6可知：电磁转矩随着转子磁极分段数的增加逐渐降低并趋于平稳.究其原因是，电磁转矩由永磁转矩和磁阻转矩两个部分共同组成.一方面，主磁场的减弱造成了永磁转矩损失一部分；另一方面，转子磁极轴向分段移位斜极后，使得直轴电感增大而交轴电感减小，从而导致了磁阻转矩受到削弱，降低了转矩脉动.

由此可见，在不影响电机输出转矩的品质情况下，对电机转子进行磁极分段，电机的输出转矩略有下降，转矩脉动也得到下降进而大幅度提升了电机的平顺性，从而达到更好的控制效果.

4 结论

在Maxwell有限元软件中建立8极48槽内置式永磁同步电机模型，对电机转子进行磁极分段移位斜极.采用解析法和有限元法，分析了永磁同步电机采用转子磁极分段移位斜极时，分段数及转子分段移位斜极角度对齿槽转矩和负载转矩的影响.根据仿真结果研究了齿槽转矩谐波削弱及转矩脉动的变化，得到如下3点主要结论.

1) 选择合适的分段移位斜极角才能使得需要削弱的谐波得到最大程度的削弱，并尽可能减小转矩损失.如果分段移位斜极角选择不佳，则有可能造成电机性能恶化.

2) 采用转子磁极按最佳移位角进行分段移位斜极的方式.在齿槽转矩中，除了次数为转子磁极分段数及其倍数次的谐波外，其余谐波基本得到消除并通过仿真得以验证.

3) 负载转矩和转矩脉动都随着转子磁极分段数的增加趋于降低.转子磁极分两段时，降低幅度较为明显，与转子磁极不分段相比，下降60%；随着转子磁极分段数增加，转矩脉动趋于平稳.