钢筋混凝土锈蚀开裂的有限元分析方法
2022-01-18陈香蓉霍静思王卫华罗漪
陈香蓉, 霍静思, 王卫华, 罗漪
(华侨大学 土木工程学院, 福建 厦门 361021)
钢筋混凝土结构保护层锈胀开裂是导致耐久性降低的主要因素之一.针对此问题,不同学者从理论模型、试验分析和数值模拟等3个方面进行了研究.即在理论方面,建立了锈裂三阶段理论[1],即铁锈自由膨胀阶段,保护层受拉应力阶段,保护层开裂阶段并建立了各自的理论计算模型;在试验方面,针对钢筋锈蚀进行了电化学加速试验[2-4]及锈蚀对构件压弯力学性能[5-9]影响评定等;在数值模拟方面,将混凝土看作骨料、砂浆及界面层组成的三向复合材料进行细观分析时,有学者基于网格[10]生成的随机凹凸型混凝土骨料可以满足富勒级数所要求的混凝土密度最大、孔隙最小[11],二维投放骨料达75%[12],满足混凝土细观分析对骨料含量的要求.
数值模拟开裂发展过程中如何进行钢筋体积膨胀率设置,以及如何通过布置级配恰当的骨料以实现裂缝延伸过程是至关重要的问题.本文针对钢筋锈蚀导致混凝土保护层开裂问题,通过投放多种随机级配骨料、并对网格映射、几何剖分、添加Cohesive单元等多种建模方法和计算效率进行对比分析.
1 钢筋锈胀导致混凝土保护层开裂模型
1.1 基本假定
通常情况下,钢筋锈蚀并引起混凝土保护层锈胀开裂受到许多因素影响,是一个随机过程.文中在模型分析过程中,采用以下4个基本假定:
1) 钢筋锈蚀为均匀锈蚀过程,并产生均匀的锈蚀膨胀应力[13];
2) 钢筋周围混凝土中产生的应力和变形仅由钢筋锈蚀引起;
3) 不考虑锈蚀产物进入到钢筋与混凝土交界面中的毛细孔和微小孔隙,即认为钢筋开始锈蚀时便对周围混凝土产生径向锈胀力;
4) 不考虑锈蚀产物进入到混凝土破坏后的微裂隙中[14].
1.2 模型建立

图1 模型横截面尺寸(单位:mm)Fig.1 Cross-section size of FE models (unit: mm)
钢筋锈蚀导致保护层开裂,属于细观尺度的结构破坏.文中利用Abaqus非线性有限元软件,建立了钢筋锈蚀导致混凝土开裂的二维有限元细观模型,并进行混凝土裂纹萌生、扩展过程及破坏形态的分析对比.设置模型尺寸为200 mm×100 mm,单元类型为CPE4R,钢筋直径为16 mm(左侧和右侧分别为钢筋1和钢筋2),保护层厚度为22 mm.有限元模型截面尺寸,如图1所示.模型底端设置固定约束,在钢筋体积随着时间均匀膨胀表征钢筋的锈蚀产物对周围混凝土产生的挤压作用.
1.3 参数设置
界面层和砂浆按文献[15]取用材料参数,精细化模型中钢筋及混凝土力学性能参数设置,如表1所示.表1中:E为弹性模量;ν为泊松比;ft为抗拉强度;ρ为密度;fc为抗压强度;a为膨胀系数.

表1 钢筋和混凝土材料的力学性能参数Tab.1 Mechanical properties ofsteel rebars and concrete material
在生成随机骨料过程中,先依据富勒级配+瓦拉文[16]获得指定级配下不同粒径范围面积比值.即
式(1)中:Dmax为最大骨料颗粒直径;di为级配骨料粒径;PK为骨料总面积占混凝土总面积的百分比;P为不同骨料集配在试件二维界面上出现的概率.
经多次骨料生成尝试,将PK设置为0.6,可实现骨料投放成功率较高,粗骨料按照级配均匀分布于钢筋混凝土截面且符合实际情况的效果[17].
骨料投放时,首先在模型中选择有限数量离散点(通常为单元几何中心或节点),判断骨料之间、骨料和容器之间位置尺寸,并设立好投放退出机制后;然后,由大到小逐个增加不同粒径范围内的骨料,当面积达到投递范围时终止生成骨料.
2 有限元模型中的骨料设置方法
在模型的分析步设置中采用Unsymmetric非线性求解,初始场变量导入钢筋体积膨胀率(n)随着时间变化曲线[18],即符合理论模型中推导[13]得到锈蚀体积膨胀速度随时间减缓的结论.随后,通过定义场变量输出时处应力、应变、位移等常规输出参数外,并输出混凝土材料DAMAGET拉伸损伤、DAMAGEC压缩损伤、SDEG刚度折减系数,以显示混凝土损伤带即裂缝位置即开展情况.
2.1 基于网格映射骨料细观模型
设置混凝土塑性损伤参数,如表2所示.表2中:ψ为膨胀角;ε为偏心率;η为黏度系数.基于网格映射骨料细观模型即在骨料周边布置薄弱材料层,通过混凝土损伤本构(CDP)描述材料损伤和失效.具体过程为,在骨料投放完成后进行网格划分,并对单元进行逐个判断,若被包含于骨料内部设定为骨料单元,而被骨料边界穿过则设定为边界单元,其他单元则设定为水泥砂浆单元.

表2 混凝土塑性损伤参数Tab.2 Parameters of concrete plastic damage
文中方法的每个单元内部材料属性相同,但由于有限元CPE4R单元天然形状,所以存在单元边界尖齿性,故而计算得到的裂缝形态也呈锯齿状.
2.2 基于几何剖分骨料细观模型
基于几何剖分骨料细观模型时,依然采用混凝土损伤本构(CDP)关系,且最终以损伤带的形式来模拟裂缝.与网格映射的精细化建模技术相比,几何剖分法在骨料投放生成之后才进行网格划分.虽然这样可能会产生部分畸变单元,但有助于实现骨料外形光滑,计算效率较高,能较好地描述骨料特征.
2.3 基于几何剖分骨料+Cohesive单元细观模型
基于几何剖分骨料+Cohesive单元细观模型是指在几何剖分骨料操作的基础上,在水泥浆体和骨料的界面区嵌入Cohesive单元模拟砂浆和骨料二者之间的界面层. 砂浆和界面层强度较低, 常用作分析结构承载下的破坏与失效过程.采用Cohesive单元属性实现裂缝扩展的描述,如表3所示.表3中:E为弹性模量;σmax为最大正应力准则;ΔFP为失效塑性位移.

表3 混凝土Cohesive单元参数Tab.3 Parameters of concrete Cohesive element
在设置Region Types时采用ElemSufs of Set,即在混凝土(包含砂浆和骨料)范围内部所有单元面之间嵌入Cohesive单元.用此方法得出的失效形式与之前两种方法基本一致,但对混凝土内部裂缝的描述效果更好.
3 有限元模型与结果分析
3.1 网格划分及计算效率对比
采用网格映射和几何剖分方法,建立钢筋锈胀导致混凝土开裂的精细化分析模型和网格划分,如图2所示.这两种方法所用的网格Global Size均为1.5.由于网格映射方法(图2(a))是先划分网格再布置骨料,因而骨料形状、尺寸皆较为均匀;但之后判定形成的骨料则因单元形状而有锯齿状;而几何剖分方法(图2(b))因先布置骨料再划分网格,骨料形态饱满圆润,网格单元则依据骨料形状布置,沿骨料边缘均匀分布并于其内部划分.因此,单元大小、形态及密度都受到骨料影响,但对于小的骨料而言单元也更加详细.

(a) 网格映射模型

(b) 几何剖分模型图2 有限元骨料布置及网格划分Fig.2 Finite element aggregate layout and mesh division
添加了Cohesive单元的模型网格划分与几何剖分模型的网格划分完全一致,只是在骨料与浆体的单元之间添加了零厚度的Cohesive单元.三种建模方法网格数目和计算效率对比,如表4所示.表4中:t为计算时间;m为步数.

表4 三种建模网格及计算效率对比Tab.4 Comparison of grid and efficiency of three modeling methods
从表4可知:在同等骨料模型情况下,采用几何剖分方法时网格数目和计算时长分别为采用网格映射方法时的1.6倍(0.94 h)和2.7倍,但对比步数可见几何剖分方法模型,其收敛速度更快.在几何剖分方法上添加Cohesive单元时计算时间和步数显著增加,计算时长和步数分别为未添加Cohesive单元时的13倍(12.5 h)和2.4倍.
在进行钢筋锈蚀导致保护层开裂模拟过程中,采用网格映射建模方法通过改变界面材料属性即可实现裂缝展示;其建模前处理较为方便且所需计算步也最少,但网格划分较粗,无法细化骨料形状,以及其与水泥浆体交接界面,适用于对局部精度要求不高的分析.采用几何剖分方法具有网格映射的效率最高、收敛速度的优点,同时也对骨料形状和交界面附近的网格进行了适当细化,但对骨料进行几何剖分需要占用较多的建模时间,效率较低.几何剖分+Cohesive单元比前两种方法的建模和分析时间成本更高且收敛难度大,但其精细化计算和描述裂缝的效果也最好.
3.2 计算结果展示分析
采用网格映射、几何剖分、几何剖分+Cohesive单元三种方法建立模型,分析得到的应力云图、裂缝开展,分别如图3所示.由图3(a)~(c)可见:三种模型骨料的投放形状、大小及位置都完全一致.从应力云图看,三种方法建立模型的计算应力分布总体上相似,在钢筋连线方向上的混凝土挤压应力较大,而混凝土保护层厚度范围内的应力较小.三种模型的结果区别在于以网格映射方式和几何剖分方式建立的模型计算结果中应力主要分布于钢筋左右两侧,采用几何剖分+Cohesive方式建立的模型,应力在钢筋周边分布更加均匀,在钢筋下方的位置也产生了轻微的应力集中和微小裂缝.

(a) 网格映射模型应力云图 (b) 几何剖分模型应力云图
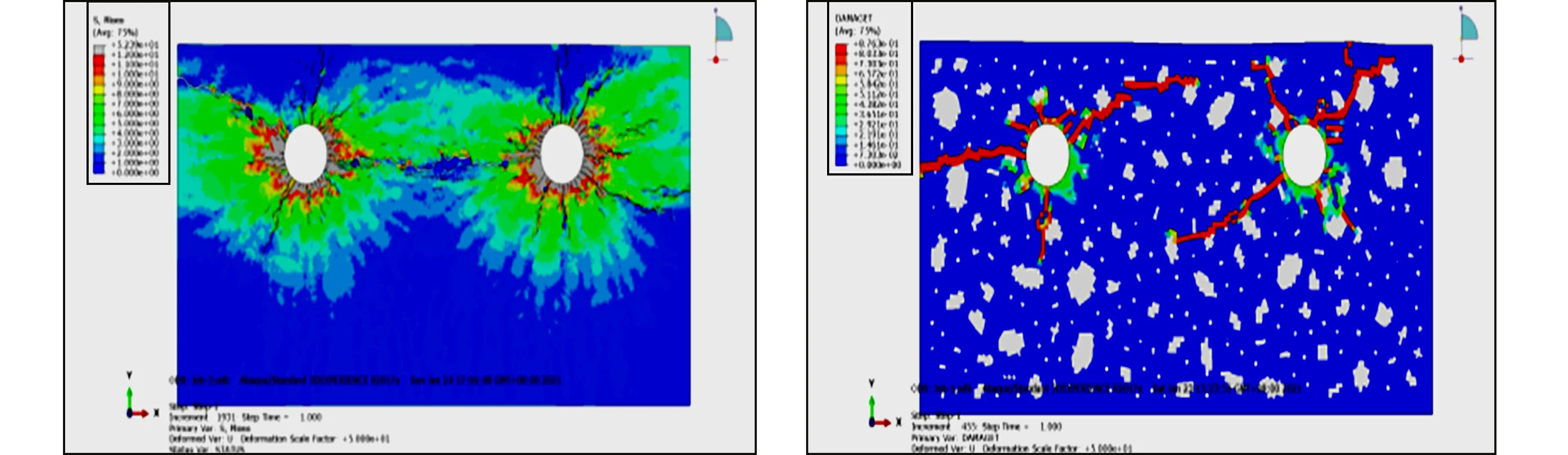
(c) 几何剖分+Cohesive单元模型应力云图 (d) 网格映射模型开裂形态

(e) 几何剖分模型开裂形态 (f) 几何剖分+Cohesive单元模型开裂形态图3 模型分析应力云图及裂缝形态Fig.3 Stress clouds and crack patternsof model analysis
从图3(d)~(f)的裂缝开展形态可见,以网格映射方式建立的模型,裂缝扩展和发展趋势总体上与几何剖分模型的计算结果相似.但是,个别主裂缝的扩展方向略有区别,如图2(d)中的钢筋1左侧主裂缝接近按水平方向扩展,而图3(e),(f)中的主裂缝扩展方向斜向10点钟方向,主要是由于钢筋附近的骨料网格差异所致(图2).
钢筋1和钢筋2之间的裂缝斜向混凝土表面方向扩展.在几何剖分方式模型分析结果中,钢筋1和钢筋2之间的裂缝呈现一定程度的贯通趋势;在几何剖分模型基础上加入Cohesive单元后,模型分析结果的裂缝分布和发展趋势与几何剖分法的结果基本一致,且可以通过节点断裂更加形象地展示裂缝分布和扩展的细节.三种模型中的钢筋2上侧的混凝土保护层均出现了开裂,且裂缝形状和发展趋势也基本一致,说明该位置的骨料网格分布对微裂缝的扩展影响不大.
骨料及裂缝细节对比,如图4所示.从图4可知:网格映射和几何剖分方法通过展示混凝土砂浆单元破坏来显示裂缝的发展趋势,而加入了Cohesive单元后得到的裂缝则是通过Cohesive单元破坏来实现的.由于网格映射方法建立的模型最终形成的裂缝是围绕骨料的薄弱层破坏,所以裂缝细节形态也呈不连续的锯齿状.几何剖分方法的网格划分是在骨料切割之后,由破坏单元形成的裂缝连续度更高.在几何剖分+Cohesive单元方法建立的模型计算结果中,裂缝形态和真实情况更接近,且呈现出个别碎石骨料贯通破坏的情况.

(a) 网格映射模型 (b) 几何剖分模型 (c) 几何剖分+Cohesive单元模型图4 骨料及裂缝细节对比Fig.4 Details of aggregate and cracks
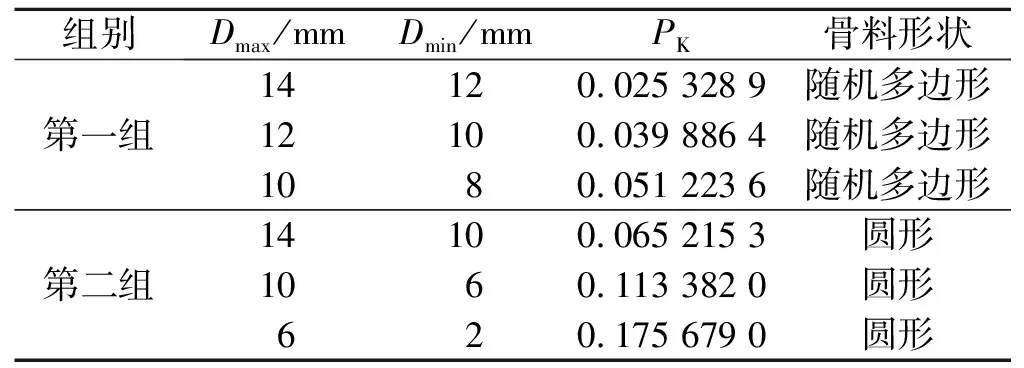
表5 骨料形状及级配Tab.5 Aggregate shapes and gradation
3.3 骨料形状级配分析
针对钢筋锈蚀导致保护层开裂,投放两组不同级配占比和形状的骨料,如表5所示.表5中:Dmax为最大粒径;Dmin为最小粒径;PK骨料占比;第一组骨料形状都为随机多边形,并设置相关长短径比值范围、边数范围等;第二组采用圆形骨料无多余参数,仅通过富勒级配+瓦拉文计算出骨料的占比.
不同骨料投放之后的模型效果对比,如图5所示.从图5(a),(b)可知:不同形状粒径及截面占比的骨料皆分布较均匀.从图5(c),(d)可知:混凝土中应力的大小和分布较为一致,钢筋1和钢筋2的左右两侧呈现应力集中分布的现象.采用两种不同的骨料进行投放,两个模型的裂缝扩展至混凝土保护层表面的时间也基本一致,约为破坏总时长的0.3处,并都处于钢筋2上方位置.

(a) 第一组骨料形状 (b) 第二组骨料形状

(c) 第一组应力云图 (d) 第二组应力云图
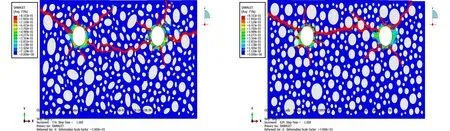
(e) 第一组裂缝形态 (f) 第二组裂缝形态图5 不同骨料模型效果对比图Fig.5 Comparison between different aggregate shapes
从图5(e),(f)可知:两组骨料形状影响裂缝扩展形态的主要差异.采用随机多边形骨料的模型则由钢筋2斜上方的裂缝扩展受到邻近骨料形状的影响,裂缝较为分散,故右侧保护层呈现了贯通裂缝(图5(e));而采用圆形骨料的模型钢筋2右上45°方向形成的贯通裂缝更加集中(图5(f)),消散了钢筋锈胀对周围混凝土的劈裂应力,因而右侧保护层未形成开裂.
3.4 模拟结果与理论对比分析
通过与钢筋锈蚀引起的混凝土保护层锈胀开裂时间(tcr)的理论模型[13]为
式(2)中:d为钢筋原始直径;c为钢筋附近厚壁圆筒厚度;k为考虑锈蚀产物进入裂缝时的锈蚀深度修正系数,加速锈蚀k初步取0.15~0.30,长期自然锈蚀k初步取0.80~1.00;混凝土泊松比νc取0.2;平均空隙厚度δ0的波动范围约在10~20 μm之间,式中取中间值15 μm;锈蚀产物的体积膨胀率n一般在2~4之间,常取2.5~3.0.
混凝土保护层锈胀开裂时间模拟值与理论值对比,如表6所示.表6中:d为钢筋原始直径;c为钢筋附近厚壁圆筒厚度;icor为加速锈蚀电流密度;Ec为混凝土弹性模量;Fk为混凝土强度标准值;tsm,tth分别为开裂时间的模拟值与理论值;e为误差.

表6 混凝土保护层锈胀开裂时间模拟值与理论值比较Tab.6 Comparison of simulation value and theoretical value of corrosion expansion and cracking time of concrete protective layer
从表6可见:混凝土开裂时间模拟值与理论计算值结果接近,误差在10%范围内,几何剖分+Cohesive单元可以在一定程度上预测钢筋锈蚀膨胀导致混凝土保护层开裂的时间.
4 结论
基于Abaqus非线性有限元软件,以钢筋锈蚀膨胀导致混凝土保护层开裂的非线性模型为例,进行了网格映射、几何剖分、几何剖分+Cohesive单元三种精细化建模方法的对比.通过对两组不同骨料形状的锈膨开裂模型的分析,得到以下5点主要结论.
1) 网格映射方法通过调整骨料和砂浆之间薄弱层的材料参数实现单元破坏显示裂缝,方式简单、计算效率高,但网格单元粗糙,局部裂缝扩展可能受到网格分布的影响.
2) 几何剖分方法的骨料形态更符合实际,运算快时间效率较高,但需要预先对骨料进行剖分,建模效率低于网格映射方法.
3) 几何剖分+Cohesive可以更加真实和精细化地模拟裂缝开展过程和形态,但计算时间和计算机运行成本较高,只适用对局部精细化分析要求较高的工况.
4) 骨料形状及布置投放会对裂缝扩展路径产生一定影响,所以在进行细观力学分析时,骨料的形状和分布应尽可能接近真实状态.
5) 通过几何剖分+Cohesive单元法建立的模型,其锈蚀开裂时间模拟值与理论计算值相比,误差小于10%,可以在一定程度上预测混凝土保护层的开裂时间.
