软悬挂撤离工况深水隔水管动力学特性分析*

柳 军 王普柽 郭晓强

(西南石油大学机电工程学院)

0 引 言

隔水管系统是海洋平台进行海底油气开采与输送中必不可少的关键设备。由于海洋环境的复杂性和多样性，隔水管的安全性和稳定性遭到了挑战，如深水钻井平台作业过程中遭遇强台风时，为避免装备发生破坏，保障作业安全，需要平台悬挂隔水管撤离避开台风。在平台撤离时，隔水管受到剧烈的风、浪、流联合作用，相比正常钻井作业，悬挂撤离隔水管系统的外部更加恶劣，大大加剧了隔水管系统损坏的风险。

深水钻井隔水管悬挂撤离方式有硬悬挂和软悬挂两种(硬悬挂方式：隔水管顶部与平台进行刚性连接，平台运动直接传递到隔水管顶部；软悬挂方式：隔水管通过张紧器与平台进行连接，伸缩节被锁死，隔水管的重力由张紧器和大钩承担)。为了确保悬挂撤离隔水管系统的可操作性，国内外学者针对硬悬挂撤离做了一系列研究，建立了硬悬挂撤离工况下隔水管一维振动模型[1-5]和纵横耦合二维振动模型[6]。部分学者[7-9]在软悬挂与硬悬挂对比研究中发现，硬悬挂的隔水管系统比软悬挂的隔水管系统对海况和干湿重力比更敏感，且相比硬悬挂，软悬挂不易导致隔水管出现动态压缩或顶部极端张力，同时上部挠性接头可以避免隔水管出现较大的横向集中载荷。孙友义等[10-11]研究了硬、软悬挂结构下超深水立管的轴向动态特性，并讨论了立管的防台风管理策略。随着数值技术的不断发展，大长径比结构的纵横向耦合效应[12-15]和大变形[16-18]越来越被学者重视，为此，一些学者用CFD仿真法和半经验法对海洋立管涡激振动展开研究[19-23]。以上研究阐述了软悬挂的可行性和优势，但现有研究主要集中于软悬挂隔水管的纵向振动或者横向振动，对软悬挂隔水管的三维振动研究不足，而且未考虑大变形和流固耦合等非线性因素的影响。

基于此，本文考虑了纵向、横流向和顺流向三向耦合，以及涡激振动和大变形等非线性因素，建立了软悬挂隔水管三维非线性振动模型，采用Newmark-β法和4阶Runge-Kutta法实现了非线性振动模型的数值求解，借助文献试验参数及数据验证了模型的正确性，探究了浮力块布置和台风重现期对软悬挂撤离钻井隔水管动态特性的影响规律，揭示了撤离工况下软悬挂隔水管振动响应特性。

1 隔水管三维非线性振动模型

1.1 模型建立

1.1.1 隔水管振动控制方程

以隔水管未发生变形时垂直轴为z轴，向下为正，取隔水管上部为坐标原点，以水流平行方向为x轴，垂直于水流方向为y轴，建立坐标系，如图1所示。υx、υy、u分别表示隔水管上任意一点在x、y、z方向上的位移。

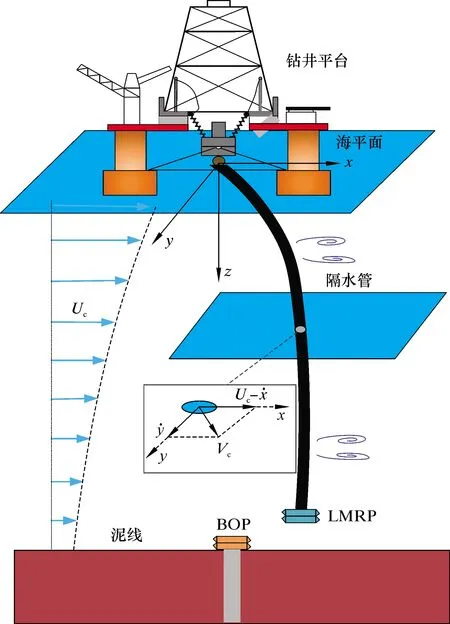
图1 隔水管坐标系及其示意图

假设隔水管为小变形，根据基尔霍夫假设：

(1)

式中：u1、u2、u3为与坐标系x、y、z对应的位移场函数。

基于给出的假设，则格林应变为：

(2)

将式(1)代入式(2)可得：

(3)

根据应变能的定义，隔水管应变能表示如下：

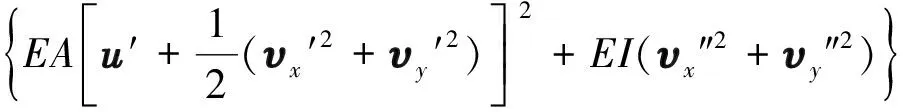
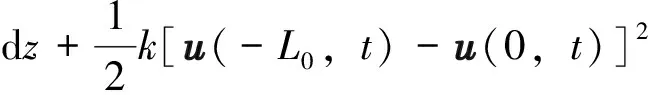
(4)

式中：E为弹性模量，Pa；I为惯性矩，m4；A为隔水管截面面积，m2。

在海洋钻井和生产过程中，隔水管与半潜船或者钻井船之间通过张紧器进行连接。张紧器等效弹簧刚度为[24]：

k=Wa/ac

(5)

式中：Wa为隔水管水下重力，N；ac为与隔水管张紧系统效率有关的常数[24]，本文取ac=10 m。

隔水管的动能可表示为：

(6)

式中：mυ为单位长度隔水管质量，kg；ρυ为隔水管密度，kg/m3；MTR为张紧环质量，kg；MLMRP为隔水管底部总成质量，kg。

结构阻尼、所受外部水动力及其阻尼所做功为：

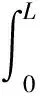
(7)

式中：Fcx、Fcy、Fcz为结构阻尼力，N；FD、FL分别为外部流体顺流方向的拖曳力与横向方向的升力，N；wg为隔水管纵向力，N。

(8)

式中：ζ为结构阻尼比；ma为单位隔水管附加流体质量，kg；ωs为简支隔水管固有角频率；Do为隔水管外径，m；ρw为海水密度，kg/m3。

根据哈密顿(Hamilton)原理和变分原理，联立式(7)和式(8)可得隔水管3个方向振动方程：

(9)

1.1.2 海洋流体力

设流体与隔水管之间的相对速度为vr，隔水管外流速度为uc。基于定常流动，作用在管子上的稳态拖曳力和升力如图2所示。

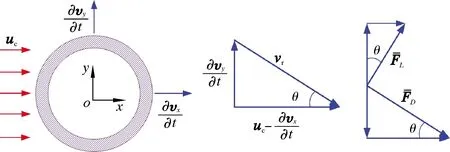
图2 作用在隔水管上的外部流体力示意图

根据Morison方程，则作用在隔水管上稳态拖曳力及升力为：

(10)

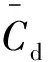
由图2可知：

(11)

作用在隔水管x方向和y方向上的稳态流体力分量为：

(12)

作用在隔水管上除了稳态的流体分量外，还包括谐和形式的脉动拖曳力和脉动升力。

(13)

式中：FD′、CD、FL′、CL分别为脉动拖曳力、脉动拖曳力系数、脉动升力及脉动升力系数。

联立式(11)～式(14)可得到作用在隔水管上的外部流体力：

(14)

采用Van der Pol非线性振动方程描述流体漩涡的脱落特性[25]，其尾流振子控制方程为：

(16)

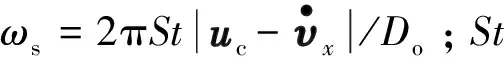
脉动拖曳力系数CD和脉动升力系数CL分别通过顺流向和横流向无量纲尾流振子变量qx和qy表示，即：

(17)

将公式(17)代入公式(15)，可得作用在隔水管上的外部流体力最终形式：

(18)

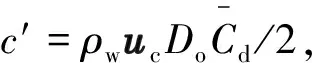
(19)

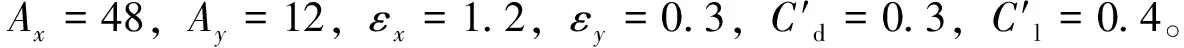
根据实际的软悬挂撤离工况，隔水管上端与张紧器连接，下端自由，模型的边界条件可以写成：

(20)

式中：uboat(t)为平台升沉运动的函数,m/s；Ku为上部挠性接头的旋转刚度，N·m/(°)。

1.2 模型求解

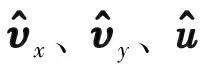
(21)

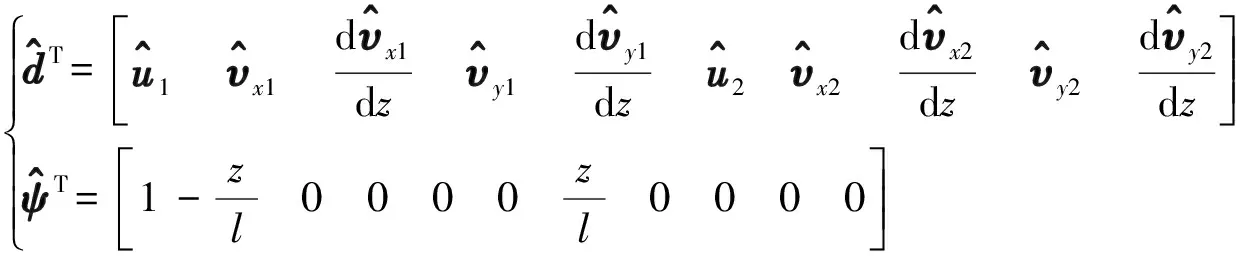
(22)

(23)

将单元隔水管控制方程进行矩阵组装，可得隔水管振动控制矩阵方程为：

(24)

式中：M为系统的质量矩阵，C为系统的阻尼矩阵，K为系统的刚度矩阵，D为系统的位移，F为系统的外力矩阵。

由于隔水管考虑了纵横向耦合因素，且隔水管模型的刚度矩阵会随着位移实时发生非线性变化，为了更好地适应隔水管非线性的影响，采用Newmark-β法[6]积分实现隔水管振动模型的数值求解，尾流振子模型采用4阶龙格库塔进行求解，求解流程图如图3所示。

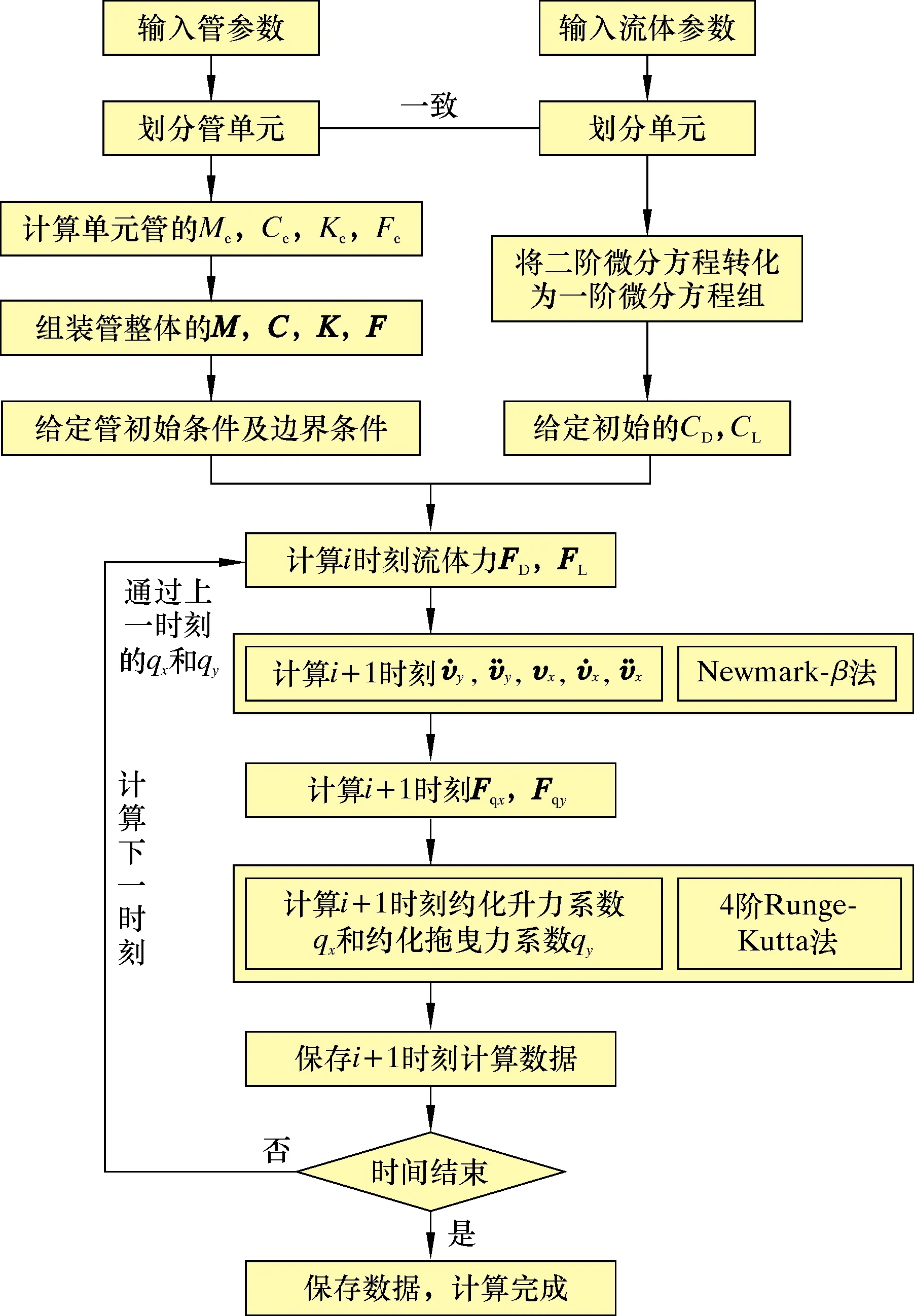
图3 钻井隔水管非线性动力学模型的求解流程

采用Fortran语言编写了隔水管非线性振动响应计算代码。

1.3 模型的验证

此案例采用SONG L.J.等[27]的试验数据进行验证，其物理试验在上海船舶运输科学研究所拖曳水池中进行，试验中上、下两端铰接。算例参数如下：隔水管长度7.9 m，水深7.9 m，外径0.030 m，内径0.027 m，顶张力2.943 kN，弹性模量108 GPa，海水密度1 000 kg/m3，单位长度隔水管质量1.768 kg/m，外流速度0.4和2.8 m/s，结构阻尼系数0.003。

边界条件使用公式(25)。

(25)

图4和图5为不同均匀外流流速下，隔水管位移均方根分布验证图。由图4和图5可知，隔水管各振动模态都与试验结果非常接近，表明本文所建模型有效。

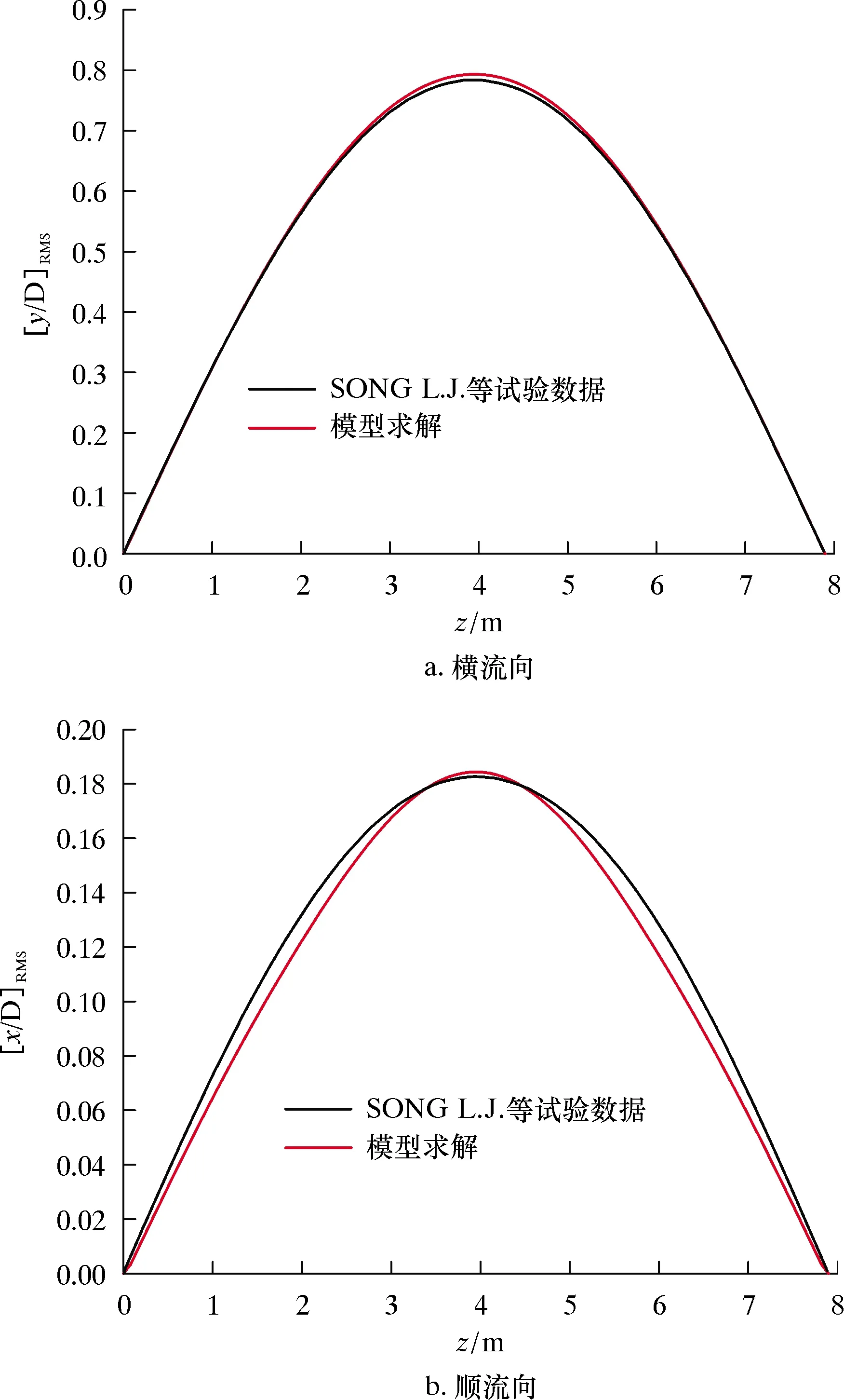
图4 外流速度U=0.4 m/s下隔水管位移均方根分布验证图

由图4还可以看出，隔水管在外流速度为0.4 m/s时，本文模型数值结果与试验在隔水管横流向与顺流向均表现为1阶振动模态，本模型所得的隔水管位移均方根数值结果与试验所得位移均方根数值结果在隔水管横流方向与顺流方向均非常接近。

由图5可知：隔水管外流速度为2.8 m/s时，隔水管在横流方向，本模型数值结果与试验所得的振动模态均表现为5阶；在顺流方向，本模型与试验所得的振动模态均表现为7阶。同时在隔水管位移均方根幅值方面，由图5a可知，隔水管横流方向上本文模型数值结果与试验结果在隔水管两端处有一定差别，但越靠近中间，两者越接近。由图5b可知，隔水管顺流方向两者结果越靠近中部越接近。这可以证明本文所采用的隔水管非线性振动控制模型及尾流振子模型对于隔水管非线性振动的模拟有效。

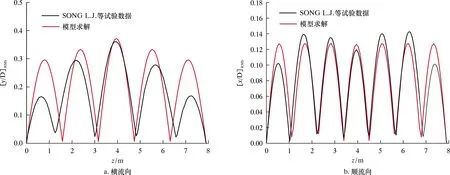
图5 外流速度U=2.8 m/s下隔水管位移均方根分布验证图

2 隔水管振动响应特性分析

基于非线性动力学模型研究软悬挂撤离中隔水管的动态行为[28-29]。计算模型的基本参数如表1所示，南海海流和海浪环境参数如表2所示。

2.1 不同浮力块布置

本节研究了不同浮力块覆盖率fp(0%、25%、50%、75%和100%)下软悬挂隔水管动力学响应，结果如图6～图8所示。相关计算参数见表1。

表1 计算模型

由图6可以看出：顺流向位移随浮力块覆盖率的增加而增加，主要是因为浮力块增加了隔水管的外径以及顺流方向上的阻力；底部处于低流速区，同时受隔水管底部总成质量的影响，中部顺流向位移时程响应的振动幅值高于底部的振动幅值。过大的顺流向位移会增加隔水管上端与月池的碰撞风险，因此，浮力块的配置比例应控制在一定范围内，不宜过大。

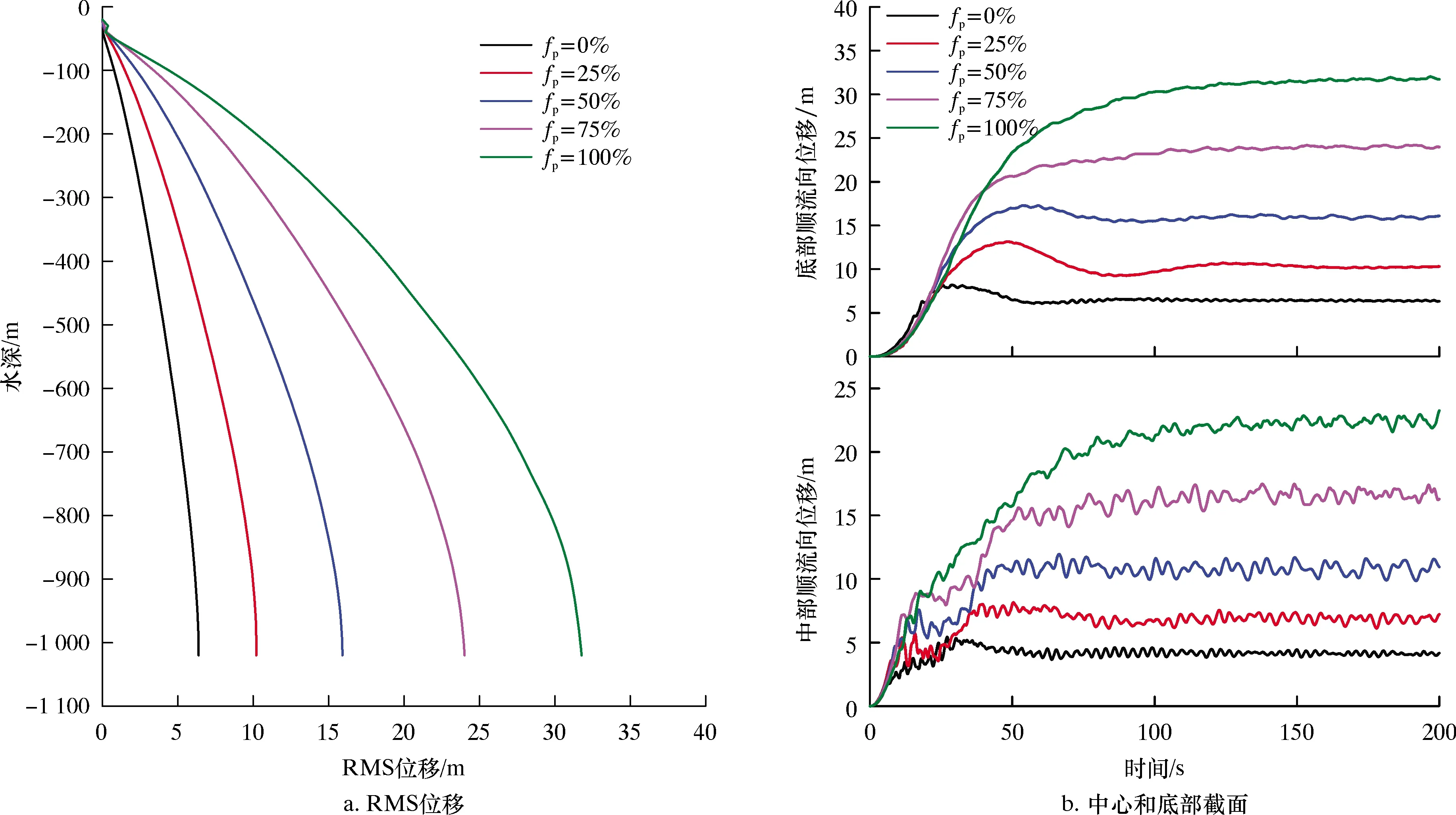
图6 顺流向的位移响应

由图7a和图7b可以看出：浮力块覆盖对隔水管横向位移均方根和应力的影响较大；隔水管最大均方根位移对应的浮力块覆盖率为75%，最大应力均方根对应的浮力块覆盖率为75%，这一结果同齐娟娟等[3]的研究结果趋势相近。值得注意的是，在覆盖率为25%的情况下，隔水管会产生较低阶的振动，同时均方根应力也较小，而在100%的覆盖率下，隔水管会产生相对高阶的振动，同时均方根应力也较大。由图7c和图7d可以看出：在50%和75%的覆盖率下横流向振动幅度更大，而且频带分布更广；在0%的覆盖率下横流向振动幅值较小，频率更高。

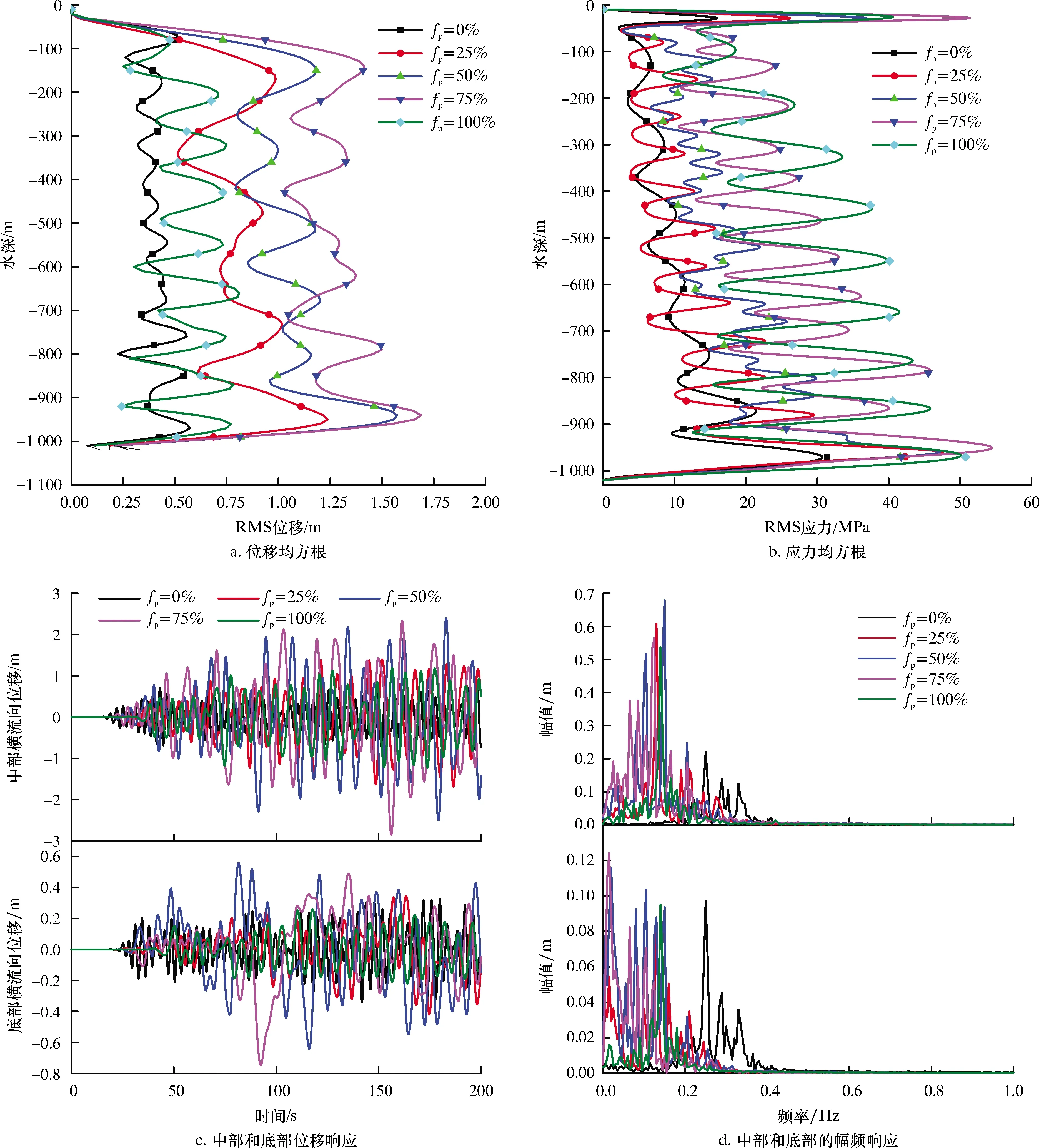
图7 横流向的位移响应

由图8a可知，浮力块覆盖度的变化对纵向振动的频率没有显著影响，但对振动的振幅有影响。由图8b可知，浮力块能有效地减小隔水管的湿重，覆盖率越高，纵向振动的位移幅值和最大动态轴力越小。

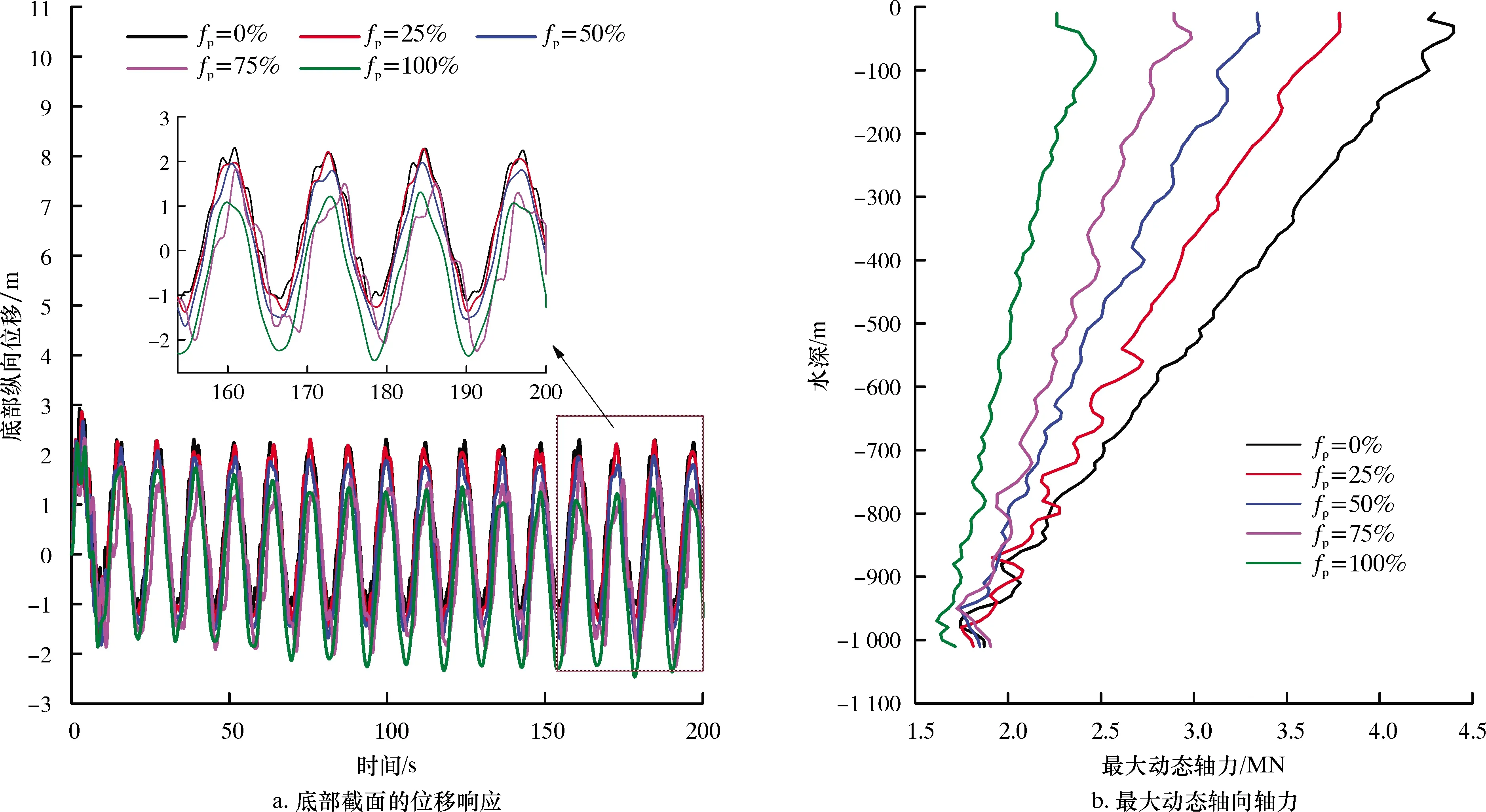
图8 纵向动力学响应

2.2 台风重现期T的影响

以 HYSY981 钻井平台在1 005 m水深下的实际隔水管系统配置为例：额定深度1 524 m的隔水管16根，额定深度为2 286 m的隔水管2根，额定深度为3 048 m的隔水管27根，壁厚25.4 mm的裸管8根(自上而下排列)。分析不同台风重现期下隔水管系统避台风撤离动力学特性响应。相关参数选取如表2和表3所示。

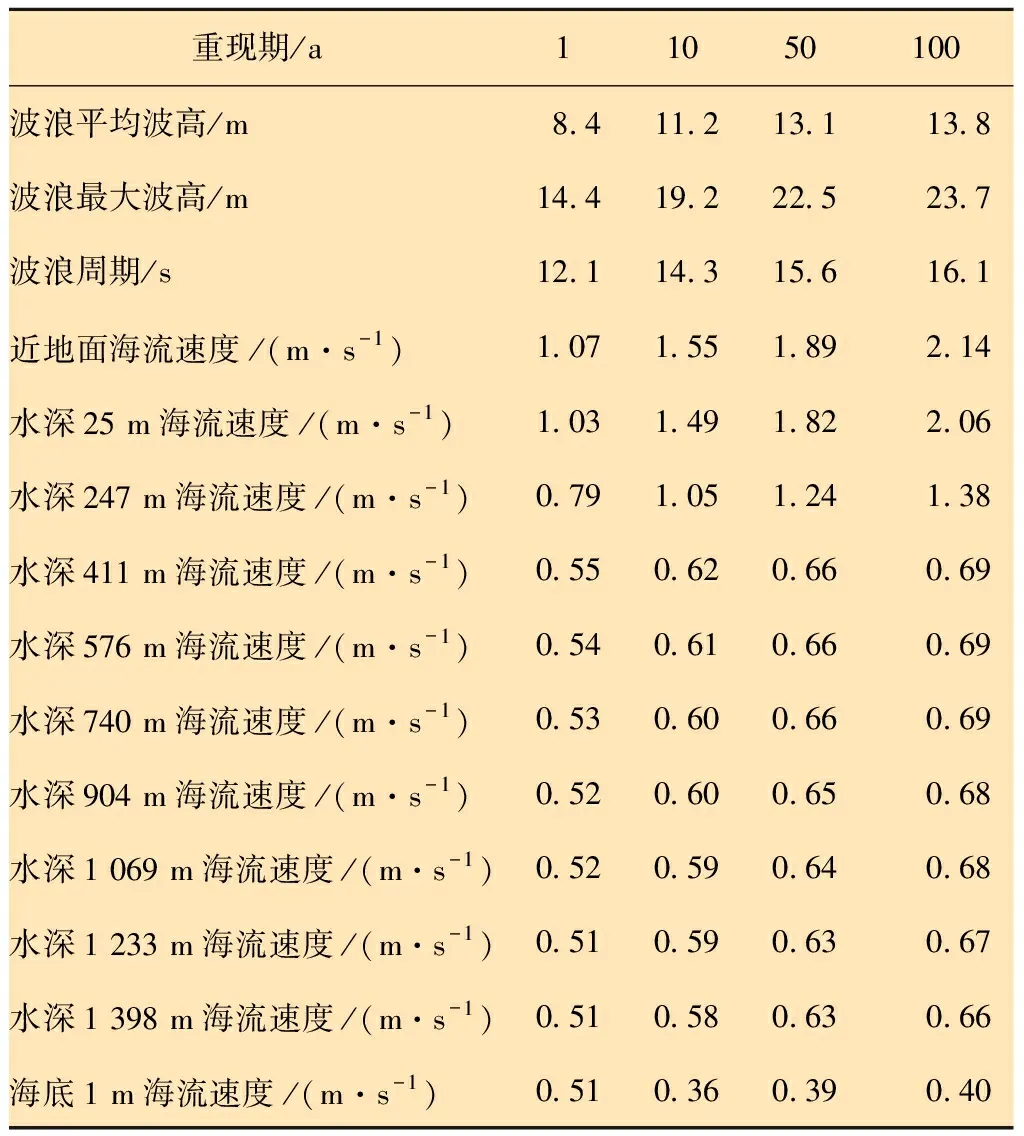
表2 南海海流和海浪环境参数[3]

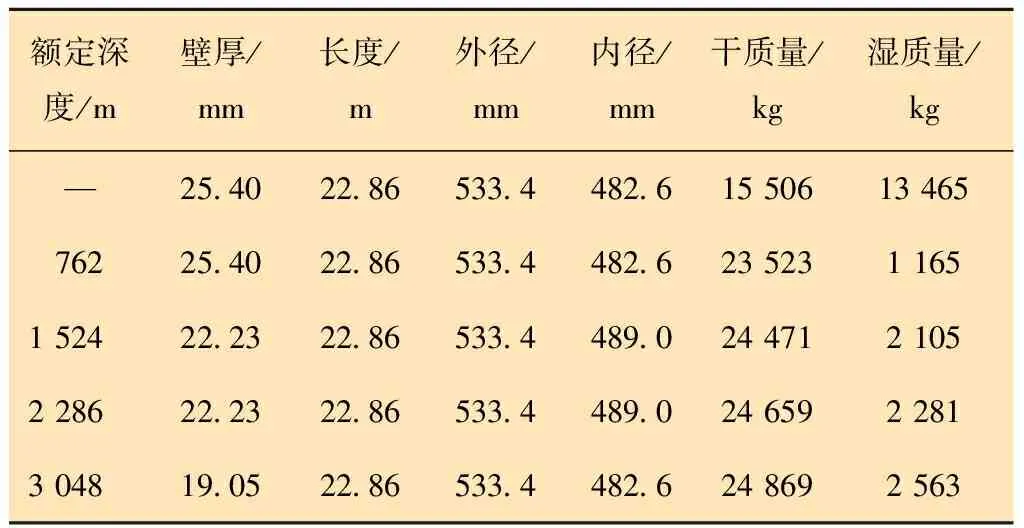
表3 HYSY981钻井平台隔水管系统基本参数[3]

分析不同台风重现期下，海流速度和平台深沉周期的变化会对软悬挂撤离隔水管动力学响应产生的影响，结果如图9所示。由图9可知，台风重现期越长，波浪和海流越大，50和100 a一遇的台风重现期下，隔水管的横流向RMS位移、横流向RMS应力和纵向位移最大，顺流向RMS位移随重现期的延长而依次增大。

由图9a和图9b可知：不同台风重现期在0～411 m水深间都处于高流速区，在靠近低端区域，4种重现期工况下的RMS位移和振动模态阶数相差不明显，而在高流速区的横流向RMS位移和振动模态阶数随着流速的增加而增加，同时变得更复杂，横流向RMS应力也随之增大；在水深800 m以下，RMS应力出现减小的趋势，这是因为在这个区域中隔水管无浮力块的影响。由图9c可知：隔水管靠近上部的弯曲程度较大，这是高流速区和浮力块导致的结果；由于高年限台风重现期的波浪幅值更大，导致纵向振动幅值更大。

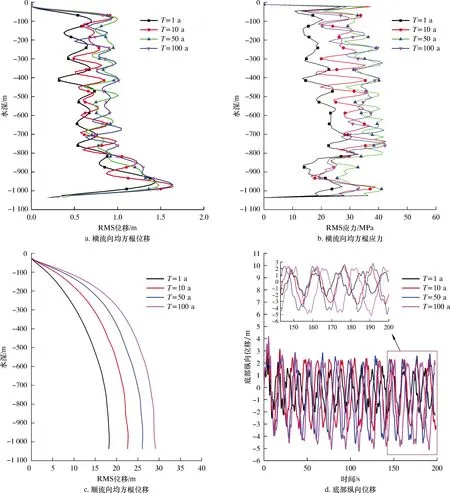
图9 隔水管动力响应

3 结 论

(1)针对紧急撤离工况下深水隔水管振动失效问题，采用有限元法并结合哈密顿变分和虚功原理，建立了软悬挂钻井隔水管三维非线性动力学模型，考虑了纵横向耦合效应、海洋涡激效应以及隔水管的大变形等非线性因素。采用Newmark-β法和4阶Runge-Kutta法实现了非线性振动模型的数值求解，借助文献试验参数和测试数据验证了理论模型的正确性，为揭示撤离工况下软悬挂隔水管响应特性奠定了模型基础。

(2)采用所建立的软悬挂隔水管非线性振动模型和南海现场参数，探究了浮力块布置模式对软悬挂隔水管振动响应的影响规律。研究结果表明，合理布置浮力块可以减小振动位移、应力和动态轴力，当浮力块覆盖率为25%的情况下，隔水管产生低阶的振动模态，同时均方根应力也较小，能够有效提高隔水管的安全性。

(3)探究了不同台风重现期工况下软悬挂隔水管的振动响应。研究结果表明，悬挂撤离工程中，流速和浮力块对隔水管的影响不可忽略，在高流速区中，隔水管的浮力块布置应该减少，在靠近顶部或者底部区域会出现应力和位移的最大值，现场需重点关注此位置处隔水管的安全性。