平椭圆弯管冲蚀磨损数值模拟*

莫 丽 郭振兴

(西南石油大学机电工程学院)

0 引 言

天然气在开采及运输中含有一些微小固体颗粒，这些颗粒以一定的速度在管道中运动并与管壁碰撞，将其动能转移到管壁上，造成管壁上的材料脱落，形成管道冲蚀磨损。已有研究证明，对于流场复杂的管道，弯管部分的冲蚀磨损是直管部分的50倍[1]。长时间的磨损会导致管道破裂，严重时甚至会产生管道爆炸，造成巨大经济损失。因此，研究弯管的冲蚀磨损机理，并采用适当的方法减小弯管的冲蚀磨损对天然气的安全运输意义重大。

影响冲蚀磨损的因素很多，例如管道材料、流体流速、颗粒直径及颗粒速度等。为了解决弯管的冲蚀磨损问题，国内外学者对弯管的冲蚀机理做了大量研究。I.FINNIE[2-3]提出了塑性材料的微切削理论，认为微切屑是塑性材料冲蚀磨损的主要原因。王凯等[4]预测了弯管冲蚀的位置，指出冲蚀较严重的区域是弯管与出口直管连接处。MENG H.C.等[5]发现，影响侵蚀程度的参数多达28个。李方淼等[6]研究了固液两相流对弯头的冲蚀规律，并分析了安装角度对冲蚀速率的影响规律。D.W.WHEELER等[7]研究发现，在节流阀内部加1层强度较高的金刚石可以显著提高抗冲蚀能力。季楚凌等[8]证明，在内壁添加肋条和凹坑的仿生弯管可以减小冲蚀磨损速率。张孟昀等[9]比较了弯管和盲通管的流动特性，指出同等条件下弯管的最大冲蚀速率明显高于盲通管。黄坤等[10]提出了3段式弯管，相比于1段式弯管，3段式弯管的流场更加平稳，弯头部分的二次流大幅降低，抗冲蚀能力也更好。C.A.R.DUARTE等[11]研究发现，在弯头处添加1个涡流腔可以有效减小弯管的冲蚀速率。

目前，学者们大多都在对圆截面的管道进行研究，并进行优化设计，很少对非圆截面的管道进行冲蚀磨损研究。为此，本文充分分析圆管的流体冲蚀特性，然后提出平椭圆管道，利用气固两相流冲蚀方程对平椭圆管道弯头进行冲蚀磨损分析，研究不同长宽比的平椭圆管道的冲蚀速率和冲蚀区域形状，从中优选出合适的长宽比，并分析不同质量流量、不同粒子直径及不同气体流速等工况下粒子对管道冲蚀的影响。所得结论可为平椭圆弯管抗冲蚀措施的制定提供参考。

1 理论模型

1.1 连续相控制方程及RNG k-ε模型

质量守恒方程：

(1)

动量守恒方程：

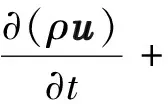
-Δp′+∇(μeffΔu)T

(2)

能量守恒方程：

∇(λΔT)+∇(uτ)+uSm+SE

(3)

式中：ρ表示连续相气体密度，kg/m3；t表示时间，s；u表示流体在3个方向的速度矢量；μeff表示等量黏度，Pa·s；p′表示修正后的压力，Pa，htot表示总焓，J/mol；p表示静压,Pa;λ表示导热系数，W/(m·K)；T表示热力学温度，K；τ表示黏性应力张量；Sm表示动力来源；SE表示能量源，W/m3。

RNGk-ε模型基于Boussinesq假设[12]提出，相比标准k-ε模型在流场计算上存在优势，而且更加精确，因此本文选择RNGk-ε模型作为计算模型。模型方程为：

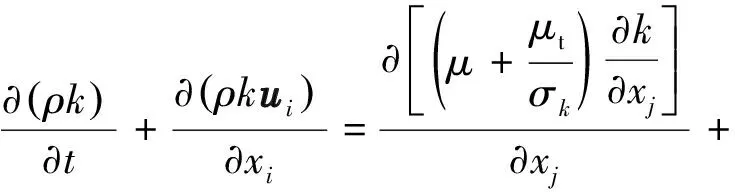
Gk-ρε

(4)

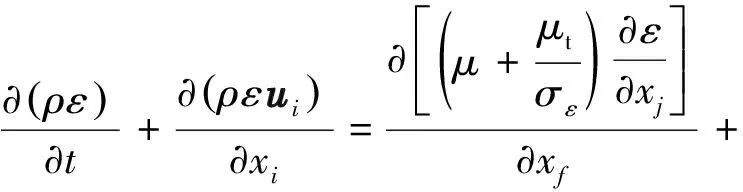
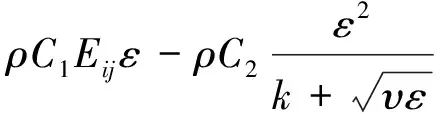
(5)

其中：σk=1.0，σε=1.2，C1=0.4，C2=1.9。

式中：k表示湍动能,J；ε表示湍动能耗散率；xi、xj表示空间坐标分量，m；μ表示气体动力黏度，Pa·s；ui表示在i方向上的速度,m/s；Gk表示平均速度梯度引起的湍动能产生项；υ表示气体运动黏度，m2/s；μt表示涡流黏度，Pa·s；Eij表示时均应变率。

1.2 离散相运动方程

在拉格朗日坐标系下，通过对粒子运动方程进行积分得到粒子的运动轨迹。在计算粒子轨迹时，假定粒子相互独立，忽略粒子间的碰撞。运动受力方程表示如下：

(6)

(7)

(8)

式中：up表示粒子速度，m/s；u表示气体速度，m/s；FD(u-up)表示单个粒子所受到的阻力，N；ρp表示粒子密度，kg/m3；d表示颗粒直径，mm；Re表示雷诺数。

1.3 壁面碰撞恢复方程

由于颗粒与壁面碰撞后存在能量损失，所以反弹速度低于入射速度。固体颗粒与壁面碰撞后速度分布如图1所示。图1中θ为冲击角。需要定义弹性恢复系数来表征粒子碰撞壁面后运动状态的变化。弹性恢复系数由法向分量en和切向分量eτ表示，其表达式为：

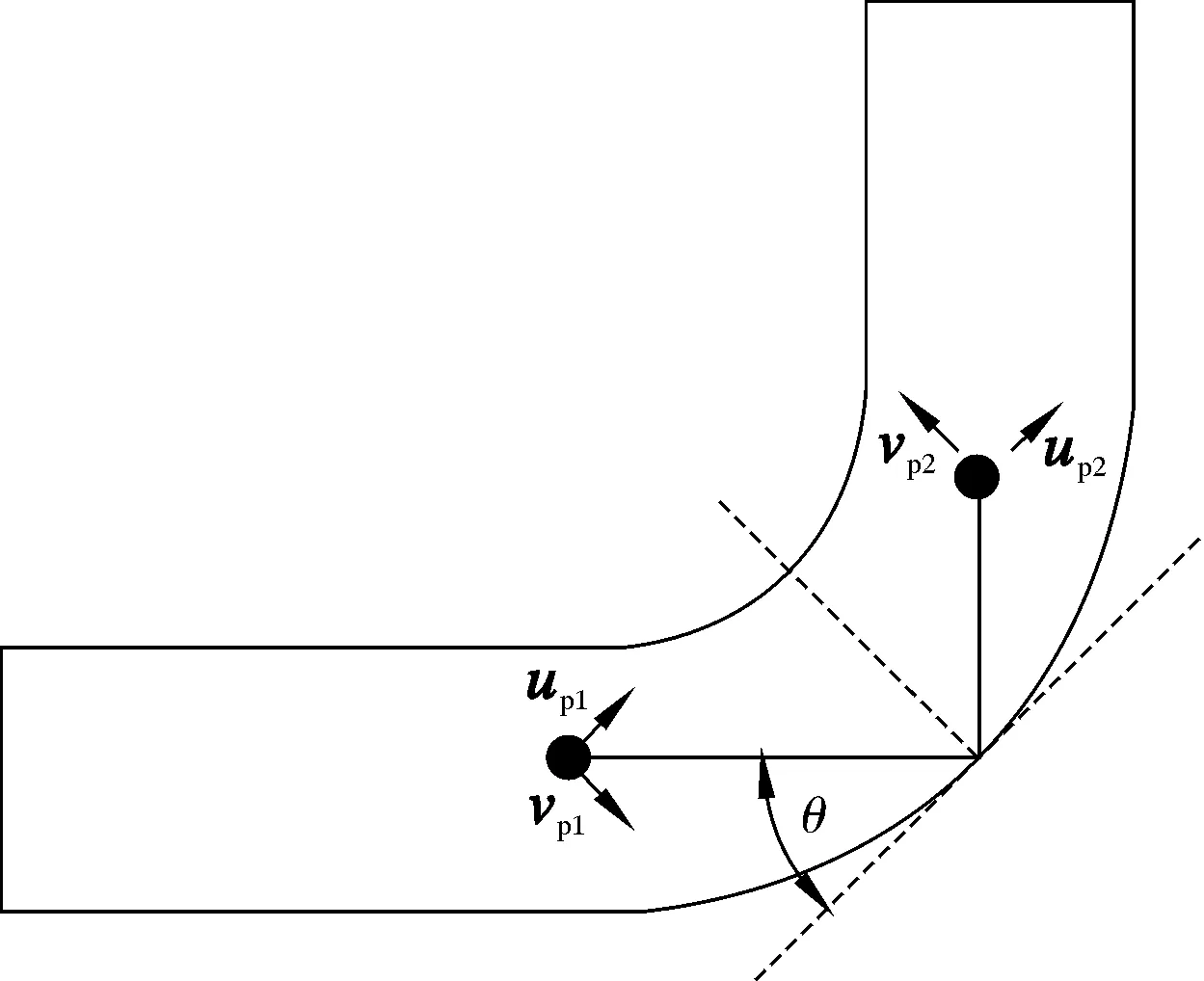
图1 固体颗粒与壁面碰撞示意图

en=up1/up2

(9)

eτ=vp1/vp2

(10)

式中：up1、up2为切向速度，vp1、vp2为法向速度。

由于大多数天然气管道是碳钢，所以选择Tabakoff模型作为本文计算模型[13]，恢复系数的计算式为：

en=0.993-0.030 7θ+0.000 475θ2-

0.000 002 61θ3

(11)

et=0.988-0.029θ+0.000 642θ2-

0.000 003 56θ3

(12)

冲击角函数采用分段线性函数，将0°、20°、30°、45°和90°的函数值分别设置为0.0、0.8、1.0、0.5和0.4。本文粒径函数采用常数1.8×10-9，速度指数函数为2.6。

1.4 冲蚀模型

本文采用Fluent软件提供的冲蚀模型作为计算的冲蚀模型。冲蚀速率ER计算式为：

(13)

2 仿真计算

2.1 CFD模型

图2展示了本文所研究的普通弯管。管道直径D=50 mm，弯曲半径R=1.5D。为了使管内流体充分流动，取入口处直管段和出口处直管段长度均为10D。

图2 弯管二维示意图

本文所研究的平椭圆管与普通圆管相比，对横截面形状做了改变，将普通圆管的横截面改为平椭圆。为了使通过气体的流动状态保持不变，选择的平椭圆管与圆管有相同的横截面积，入口处直管长度和出口处直管长度保持不变，另外弯头处的弯曲半径也保持相同。对平椭圆管的长度a和宽度b取不同的值，得到不同的长宽比K(K=a/b)。平椭圆管端面参数如表1所示，横截面形状如图3所示。

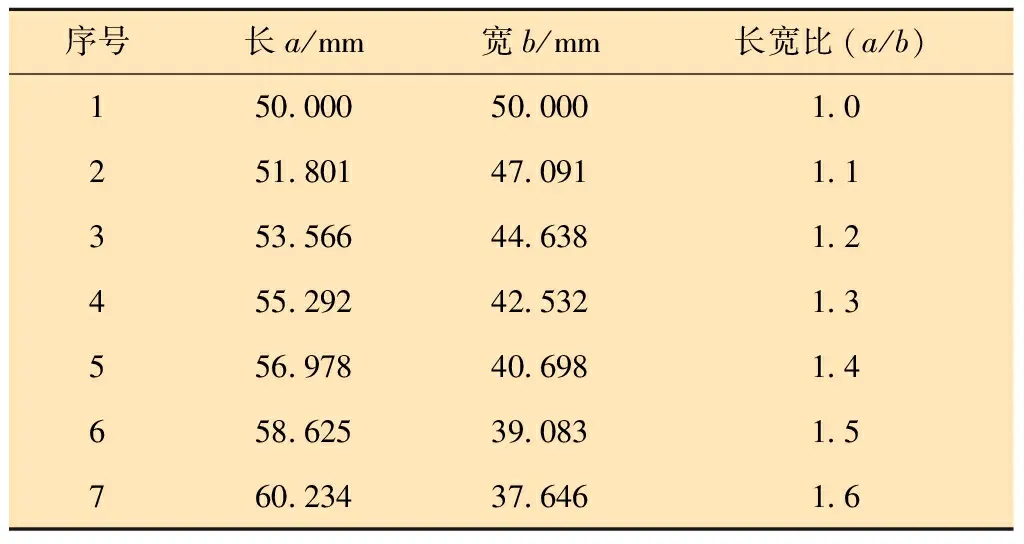
表1 平椭圆管端面相关参数

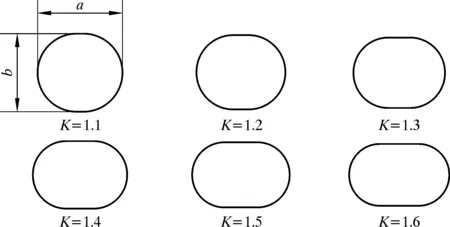
图3 平椭圆管横截面示意图

2.2 边界条件

本文气相为连续相，砂粒为离散相。所使用的气相为甲烷，密度为0.667 9 kg/m3，黏度为17.071 mm2/s。固体颗粒密度为1 500 kg/m3。对于气相，采用RNGk-ε模型作为计算的湍流模型，入口采用速度入口，出口采用压力出口。在injection中设置注入颗粒速度、颗粒直径和质量流量，其中颗粒速度与气体速度保持一致。动量和湍动能采用二阶迎风离散格式，求解器选择半隐式SIMPLE算法。

2.3 网格无关性验证

对模型进行网格划分，划分方法采用扫掠。图4为模型的网格划分图。由于管壁处黏性底层的存在，对网格添加10层边界层，且对弯管部分进行局部加密。在仿真过程中，网格的数量、大小和质量都会影响仿真结果，为了减小网格划分对结果产生的影响，有必要进行网格无关性验证。选用网格数量为124 488、230 496、309 464、477 420、679 679及1052 932的模型分别进行数值模拟，结果如图5所示。由图5可知，当网格数量达到477 420后，网格数量对仿真结果的影响较小，达到网格无关性要求。

图4 模型网格划分图

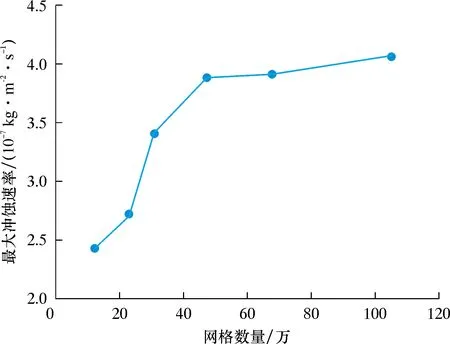
图5 最大冲蚀速率与网格数量的关系曲线

3 结果分析和讨论

3.1 长宽比对最大冲蚀速率的影响

图6展现了当粒子直径为0.2 mm、质量流量为0.001 kg/s、速度为10 m/s时，不同长宽比下平椭圆弯管的冲蚀速率云图。其中：当长宽比K=1.0时，该管为普通圆管，此时冲蚀区域集中，总体呈椭圆形，且中心区域冲蚀较严重。同时，弯头靠近出口处形成了2个长条的冲蚀区域(类似V形)，这与文献[14-15]得出的结论一致。随着长宽比逐渐增大时，冲蚀区域中心的冲蚀率逐渐下降。当长宽比K=1.2时，冲蚀区域中心的冲蚀速率开始降低，冲蚀较严重区域不再集中，开始分散。另外，弯头靠近出口处的V形区变成了三角形。随着长宽比继续增大，冲蚀较严重区域向两侧转移，冲蚀区域中间的冲蚀速率越来越低。当长宽比K=1.6时，冲蚀区域已经由椭圆形变成了U形。

图6 不同长宽比下弯管的冲蚀速率云图

图7为长宽比与最大冲蚀速率的关系曲线。由图7可知：随着长宽比的增大，最大冲蚀速率逐渐降低；当长宽比K=1.1时，最大冲蚀速率从3.89×10-7kg/(m2·s)下降到3.51×10-7kg/(m2·s)，下降了9.8%；当长宽比K=1.2时，最大冲蚀速率下降到3.30×10-7kg/(m2·s)，下降了15.2%；当长宽比K=1.3时，最大冲蚀速率下降到3.16×10-7kg/(m2·s)，下降了18.8%；随着长宽比增大，最大冲蚀速率下降幅度越来越小。当长宽比大于1.4时，最大冲蚀速率已经到达一个相对较低的值，再继续增大长宽比，最大冲蚀速率下降不再明显。因此，长宽比K=1.4为较为理想的参数，此时与普通圆管比较，最大冲蚀速率下降了21.9%。

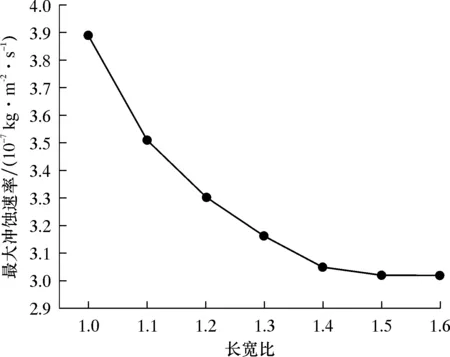
图7 长宽比与最大冲蚀速率的关系曲线

查看长宽比K分别等于1.0和1.4时的颗粒轨迹图，如图8所示。由图8可知，粒子在直管段运动平稳，经过弯头时，粒子在A1、A2区域与弯头壁面碰撞。当K=1.0时，在壁面的作用下，管壁左边的粒子开始向右移动，管壁右边的粒子开始向左边移动，两边的粒子在B1区相交，导致B1区的冲蚀较其余区域严重。相比于K=1.0的圆管，当长宽比增大时，两边发生交错流动的粒子数量减小，并且相交的区域B2更大，这一现象导致冲蚀的区域更大，因此冲蚀磨损现象减弱，呈现在冲蚀云图上就出现了随着K的增大，弯头中间冲蚀速率下降的现象。另外，平椭圆管外壁被冲蚀的区域也比普通圆管大，从而使最大冲蚀速率降低。

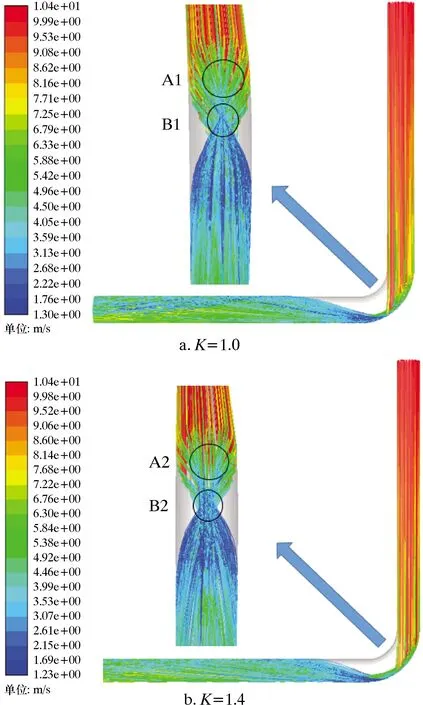
图8 2种管道下的粒子运动轨迹

粒子的冲蚀角度同样会影响弯头的冲蚀速率。张奇超[16]研究了天然气集气管道的冲蚀现象，得出当冲击角从0°增加时，冲蚀磨损速率会升高，当冲击角达到45°时冲蚀磨损速率最高，然后又逐渐降低。对比如图9所示的普通圆管和长宽比等于1.4的平椭圆管模型后发现，平椭圆管中心线处的冲击角较小，意味着平椭圆管粒子的平均冲击角比圆管小，最大冲蚀速率也因此而降低。

图9 2种管道的冲蚀角对比

当长宽比K=1.4时，管道内压力云图和速度云图如图10所示。

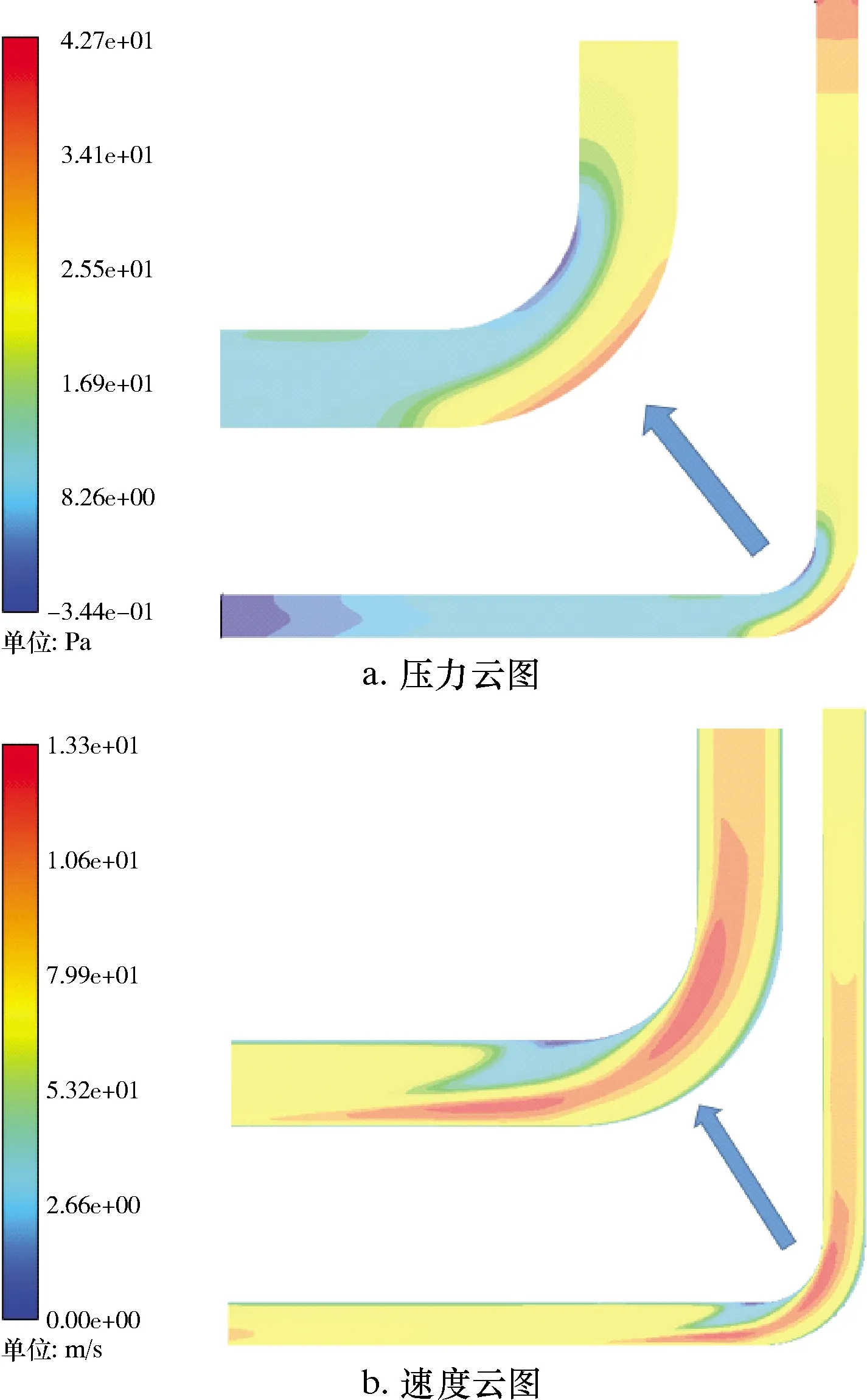
图10 长宽比为1.4时管道压力云图与速度云图

由图10可知，在弯头处出现了最大压力区和最高流速区。这是因为弯头处气体会产生较大的离心力，气体在离心力的作用下挤压弯头外壁，导致外侧的压力增大而内侧压力减小。弯头内侧流体的比压能转换成动能，导致内侧流体的流速升高。不同长宽比管道的最大压力和最高流速曲线如图11所示。由图11可知：随着长宽比增大，最大压力会在小范围内波动，波动幅度为2.5%；最高流速有略微降低，长宽比每增加0.1，流速降低0.7%。

图11 不同长宽比时管道内压力与速度曲线

3.2 粒子直径对冲蚀速率的影响

为研究不同粒子直径对长宽比K=1.4的平椭圆管冲蚀速率的影响，当粒子质量流量为0.001 kg/s、速度为10 m/s时，取粒子直径为0.2～1.0 mm进行分析，结果如图12所示。

由图12可知：粒子直径对最大冲蚀速率有直接影响，当粒子直径小于0.5 mm时，随着粒子直径增大，最大冲蚀速率升高，这是因为当粒子直径增大时，单个粒子所具有的动能会增大，从而对管壁造成更大的冲蚀；当粒子直径大于0.5 mm时，最大冲蚀速率先降低后升高，这是因为随着粒子直径增大，粒子之间的碰撞加剧，使粒子产生能量损失[17]，甚至使粒子破碎，于是最大冲蚀速率先降低，后由于粒子动能继续增加，冲蚀速率因此也继续升高。不同粒子直径下的冲蚀速率云图如图13所示。由图13可知，随着粒子直径的增大，冲蚀区域并不会有大的变化。因此在实际工况中，控制粒子直径能有效减轻粒子对弯管的冲蚀现象。

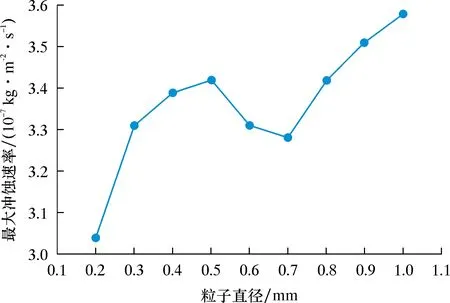
图12 粒子直径和最大冲蚀速率的关系曲线

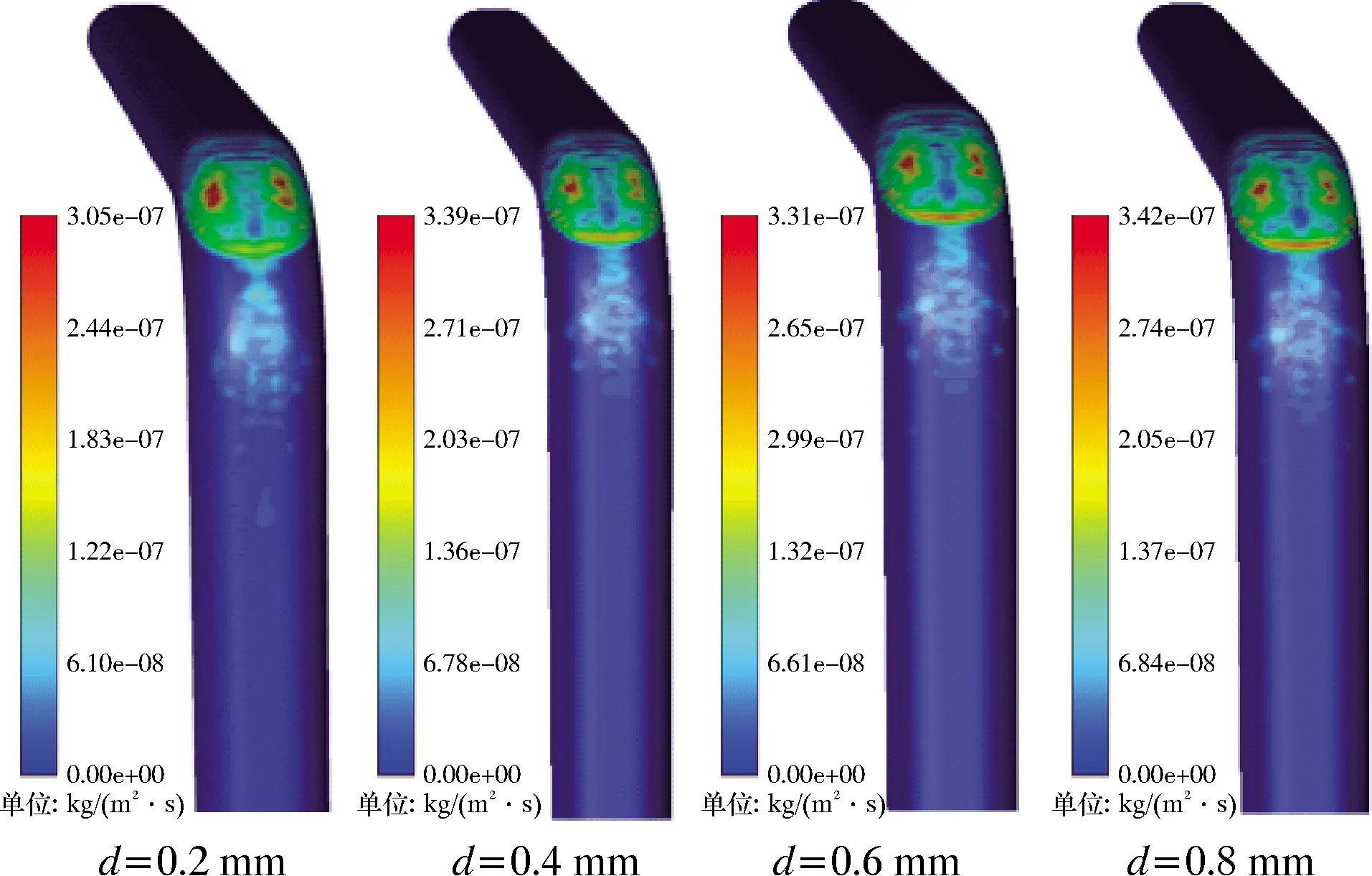
图13 不同粒子直径下的冲蚀速率云图

3.3 气体流速对冲蚀速率的影响

当粒子直径为0.2 mm、质量流量为0.001 kg/s、平椭圆管长宽比为1.4、粒子与气体速度相同时，分析不同气体流速对管道冲蚀磨损的影响，结果如图14所示。从图14可以看出，随着流速升高，粒子对弯管的冲蚀越来越严重。这是因为速度升高后，粒子所具有的动能随之增加，从而加重了冲蚀。观察速度为5、10、15和20 m/s时的冲蚀云图，如图15所示。当流速较低时，冲蚀严重的区域主要是弯头与入口段连接时，这是因为粒子直接与壁面碰撞。随着流速升高，弯头与出口连接处也逐渐出现了冲蚀严重区域，这是因为管壁左右两边的粒子流在此处交汇，随着流速升高，粒子对此处的冲蚀也随之加剧。

图14 气体流速与最大冲蚀速率的关系曲线

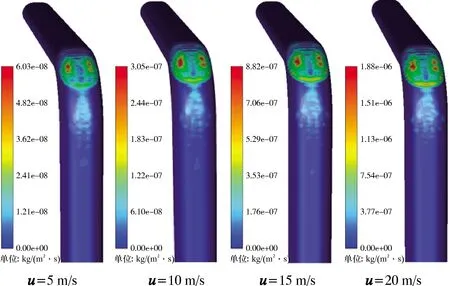
图15 不同气体流速时的冲蚀速率云图

3.4 质量流量q对冲蚀速率的影响

当粒子直径为0.2 mm、气体速度为10 m/s、长宽比为1.4、粒子与气体速度相同时，取不同的粒子质量流量进行分析，结果如图16所示。

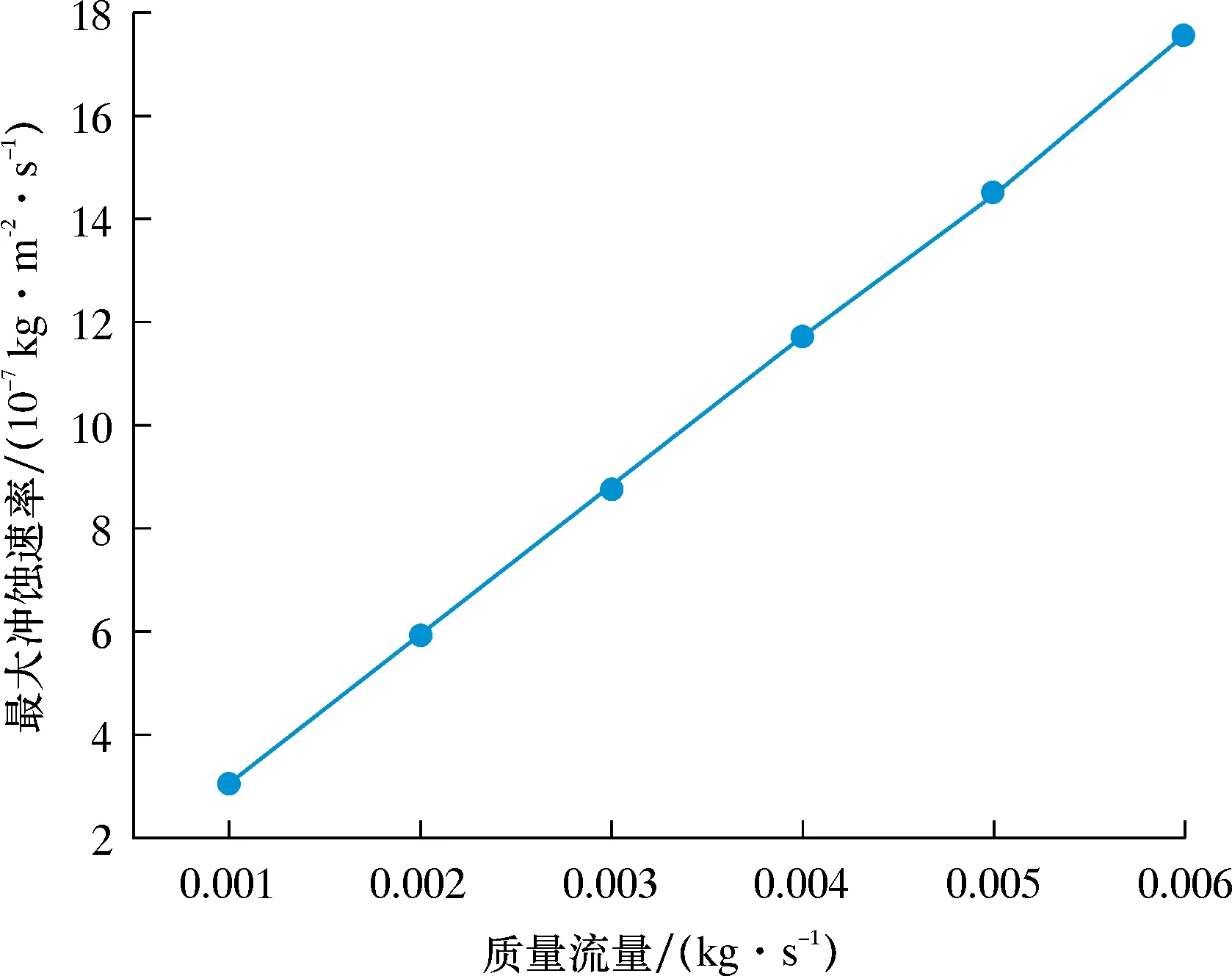
图16 质量流量与最大冲蚀速率的关系曲线

由图16可知，随着质量流量的增大，粒子对弯头部分的冲蚀越来越严重，冲蚀最严重的区域依旧是弯头外壁两侧面，而且增长率呈线性增长。这是因为粒子质量流量增大时，单位时间内流过管道的粒子数也增多，导致与管壁碰撞的粒子数量也增加，从而加重了冲蚀。图17为不同质量流量下的冲蚀速率云图。由图17可知，当质量流量不同时，冲蚀的区域并无明显变化。因此质量流量增大不会对管道冲蚀区域产生影响，但是会显著增加冲蚀速率。

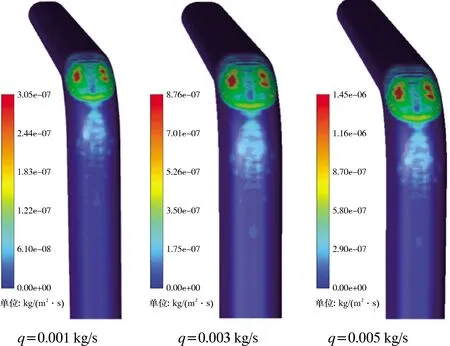
图17 不同质量流量下的冲蚀速率云图

4 结 论

(1)相比于普通圆管，平椭圆管能明显降低最大冲蚀速率，随着平椭圆管长宽比的增大，最大冲蚀速率逐渐下降。当长宽比达到1.4后，最大冲蚀速率下降的速度明显降低，因此认为平椭圆管最适宜的长宽比为1.4，此时最大冲蚀速率下降了21.9%。

(2)平椭圆管的粒子冲击角比普通圆管的粒子冲击角小，平椭圆管的被冲蚀面积比普通圆管的被冲蚀面积大，因此其最大冲蚀速率比普通圆管低。

(3)当粒子直径增大时，平椭圆管弯头处的最大冲蚀速率先升高、后降低、再升高，冲蚀的区域基本保持不变。当质量流量增加时，平椭圆管弯头处的最大冲蚀速率也会升高，且呈线性相关，冲蚀的区域基本保持不变。当气体流速升高时，平椭圆管弯头处的最大冲蚀速率也会升高，且呈非线性指数相关，弯头和直管段连接处的冲蚀现象会逐渐加重。