双梯度钻井关键工具及井筒压力动态变化规律*
2022-01-18张锐尧柳贡慧杨宏伟王江帅
张锐尧 李 军,2 柳贡慧,3 杨宏伟 王江帅 文 涛
(1.中国石油大学(北京) 2.中国石油大学(北京)克拉玛依校区 3.北京工业大学 4.塔里木油田分公司)
0 引 言
随着我国经济的快速发展,对于能源的需求也日益增加,对外依存度也越来越高[1-3]。由于我国海域油气资源丰富,为了增加油气产量,近年来深水油气资源逐渐发展成为我国油气勘探开发的重要接替区[4-5]。但是深水区环境复杂,特别是孔隙压力高、破裂压力低所形成的窄压力窗口[6],如果利用常规钻井方法则极易引起溢流或漏失等井下复杂情况的发生,同时井深结构也变得更为复杂,显著降低了经济效益[7]。
近年来,美国能源部首次提出了“空心球双梯度钻井”的概念。2017年,李军首次提出了将多梯度钻井和控压钻井相结合的思想,该技术有望成为解决窄压力窗口钻井难题的新方式。双梯度钻井技术就是利用分离器直接将低密度空心球分离进入环空中,从而改变环空中钻井液的密度梯度,进一步增加可控压力范围,达到以最优井身结构钻至目标井深的目的。2019年,王江帅和廖超等[8-9]研制了旋流分离器,并利用室内试验对分离效率进行了研究,但是分离效果并不理想。
本文针对目前所面临的旋流分离器分离效率不高的技术瓶颈,研究出了能够实现高效分离的过滤分离器。依据多孔介质的过滤原理[10],该分离器的显著特征在于只要满足过滤结构中的滤网孔径小于空心球的直径,则空心球无法顺利穿过滤网,从而实现分离。本文先对过滤分离器的结构以及工作原理进行了介绍,然后通过数值模拟与室内试验对其分离效率进行了验证。基于该过滤分离器,推导了分离过程中产生的波动压力的数学模型,并进一步建立了双梯度钻井井筒压力预测模型。最后研究了在不同的空心球体积分数变化率、过滤分离器位置及机械钻速等条件下的井筒压力的动态变化规律。研究结果可以为窄压力窗口条件下的安全钻进提供理论基础与技术支撑。
1 关键工具研究
1.1 过滤分离器结构
过滤分离器二维结构如图1所示。过滤分离器主要由上接头,第一、第二、第三级外筒,第一、第二级流道,套筒,过滤结构(含金属过滤网与球形过滤塞)以及下接头等组成。其中金属过滤网覆盖在球形过滤塞的上部,球形过滤塞的球形面上开有呈圆周等距分布的通孔(见图2),可以保证钻井液正常通过过滤结构,而不会对进入下部钻柱的排量产生影响。过滤分离器短节通过上、下接头与钻柱相连。

1—上接头;2—螺栓;3—第一级外筒;4—第二级外筒;5—套筒;6—第三级外筒;7—过滤结构。

图2 过滤分离器与过滤结构的三维结构
1.2 工作原理
在钻井过程中,先将空心球与钻井液混合均匀后从上部钻柱注入,然后混合流体进入过滤分离器的内腔,之后流经过滤结构。由于空心球的直径大于金属过滤网的孔径,所以空心球无法穿过过滤网而短暂停留在球形过滤网的表面,然后在钻井液的不断冲刷作用下,空心球会从分离口顺利进入到上部环空中。上部环空中为低密度空心球与钻井液的混合流体,而下部环空中为原钻井液,所以以过滤分离器为参考点,在上、下两个环空中形成了两个密度梯度。
1.3 分离效率研究
1.3.1 室内试验
图3为双梯度钻井室内循环系统,该系统主要由控制柜和模拟循环系统组成。控制柜与软件用于调节泵的排量与阀的开闭。模拟循环系统包括模拟钻柱以及环空。循环系统的工作原理如图4所示。先将空心球与钻井液的混合流体从钻柱的上部入口处注入,再经过滤分离器分离后,部分钻井液与空心球从分离口排出,最终回到储集池1中。其余钻井液则进入底流口,并返回到储集池2中。当本次循环结束后,根据储集池1中所得空心球体积分数与注入的空心球体积分数对比,从而得到空心球的分离效率。然后调节泵的排量或空心球的体积分数,继续进行分离试验,最后得到如图5所示的试验结果。

图3 双梯度钻井室内循环系统
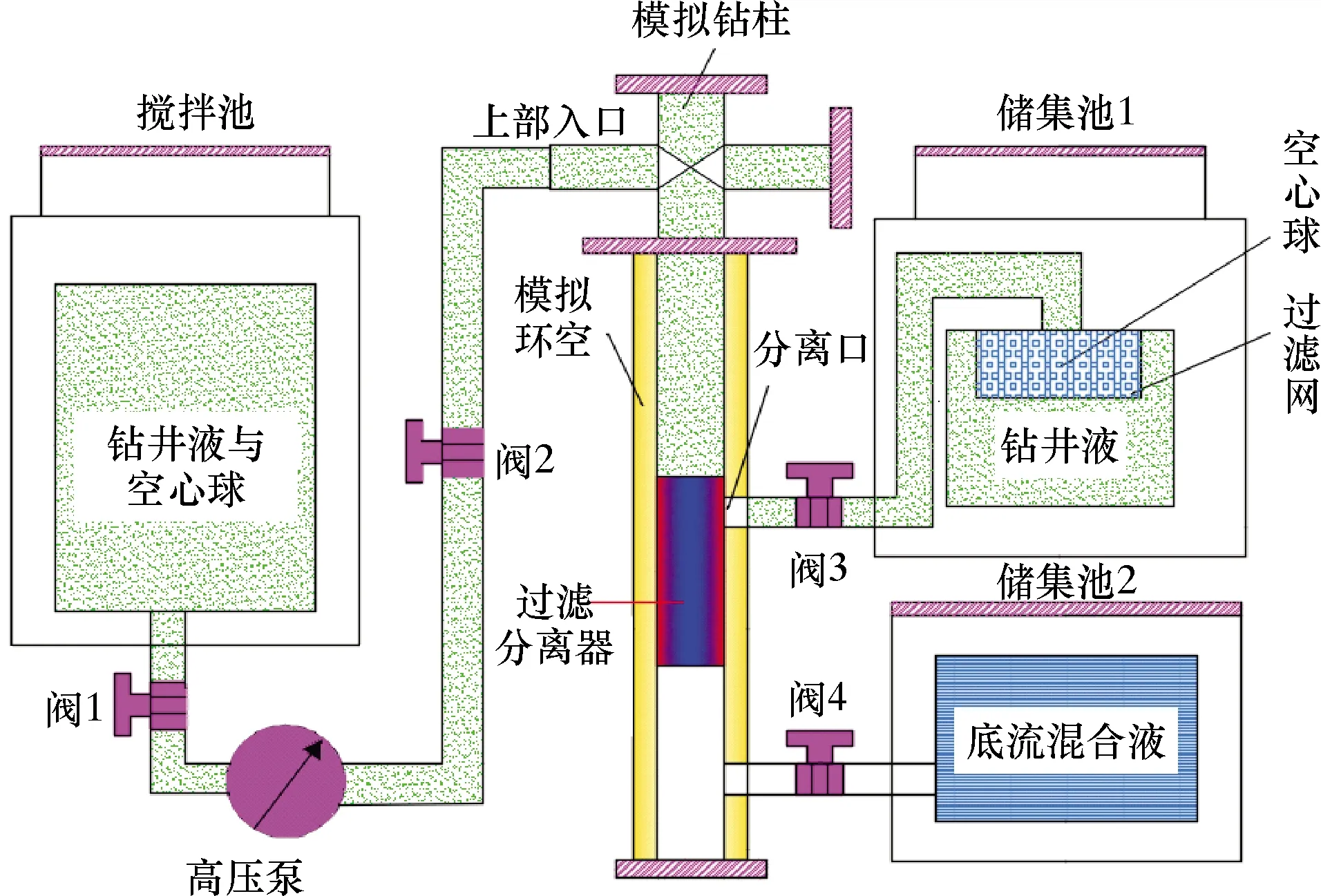
图4 循环系统的工作原理

图5 分离效率的数值模拟结果
随着钻井液的排量与空心球体积分数的增加,分离效率不断增加。排量的增加会显著增强流体的冲刷作用,使得滞留在钻柱内以及金属过滤网表面的空心球减少,从而提升分离效率。空心球的体积分数增加,增加了球-球接触面积,进一步减小了钻井液的曳力,更加有利于空心球的分离。综合数值模拟结果与室内试验结果,过滤分离器的最高分离效率可以达到98.5%。通过数值模拟与室内试验,验证了过滤分离器可以实现对空心球的高效分离。
1.3.2 数值模拟
由于过滤分离器对空心球的分离过程类似于滤纸、多孔滤板等多孔介质的过滤过程[11],所以本文基于多孔介质力学模型与欧拉多相流模型对过滤分离器进行流场仿真。分别研究了混合流体在不同的注入速度以及不同的空心球体积分数的条件下,过滤分离器分离效率的变化规律。图6为分离效率的室内试验结果。
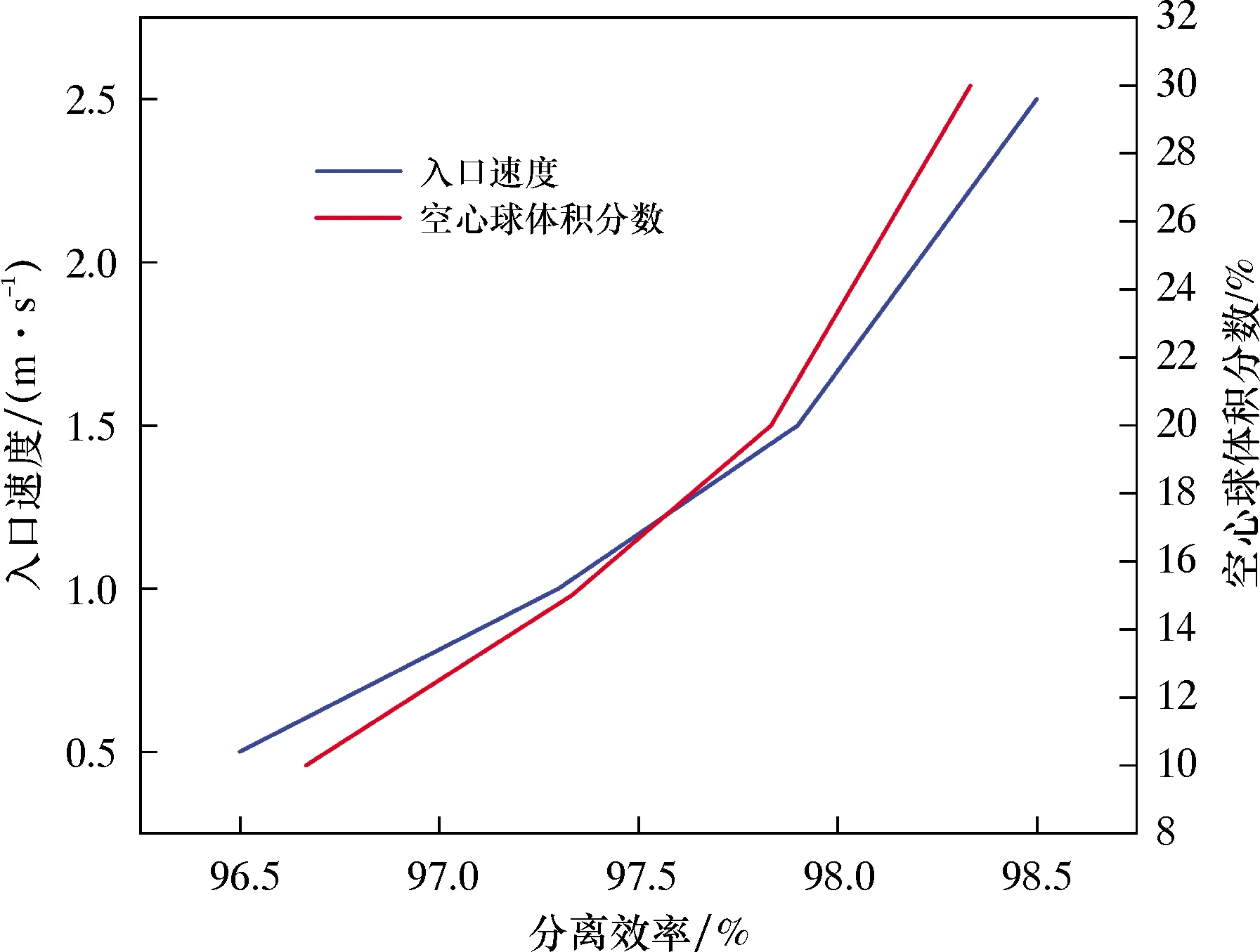
图6 分离效率的室内试验结果
由图6可以看出,随着注入速度与空心球体积分数的增加,分离效率也逐渐升高,最高分离效率可以达到98.5%。因为随着注入速度的增加,停留在金属过滤网表面的空心球受到钻井液的冲刷作用增强,有利于空心球进入到环空中;而空心球体积分数的不断增加,有利于增加球-球接触面积,从而减小钻井液对空心球的曳力作用,这也有利于空心球的分离。
2 井筒压力动态变化规律研究
2.1 波动压力研究
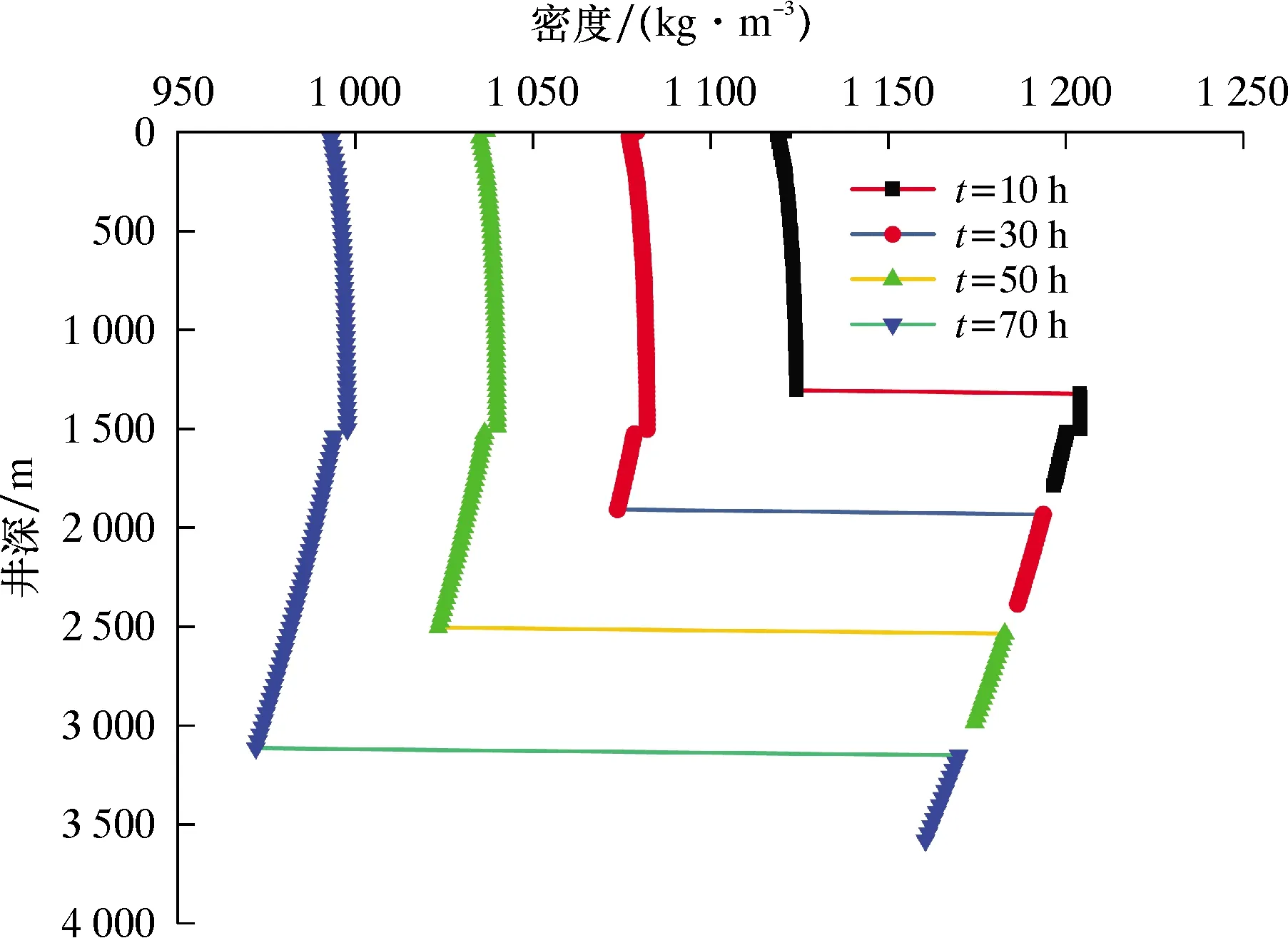
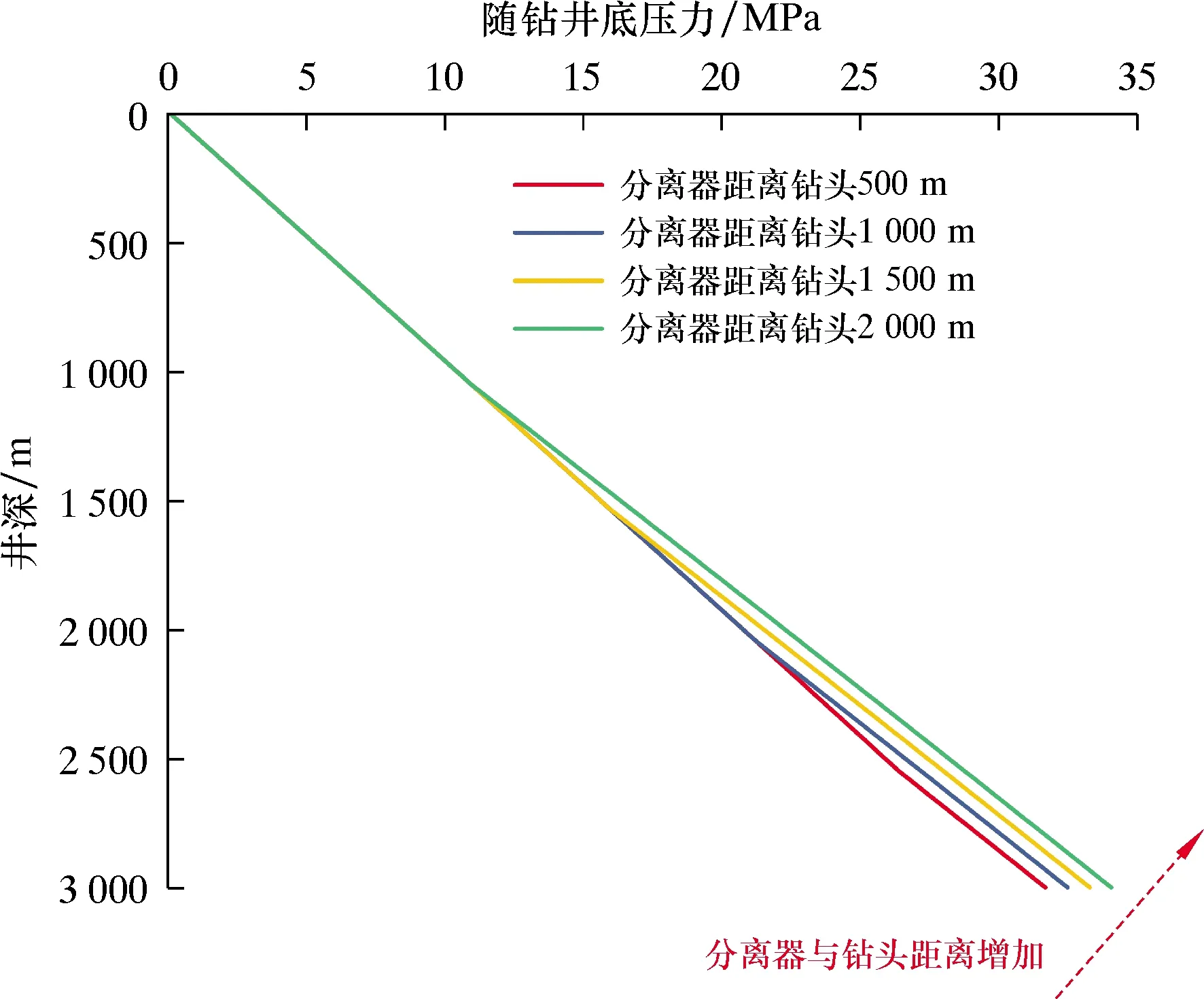
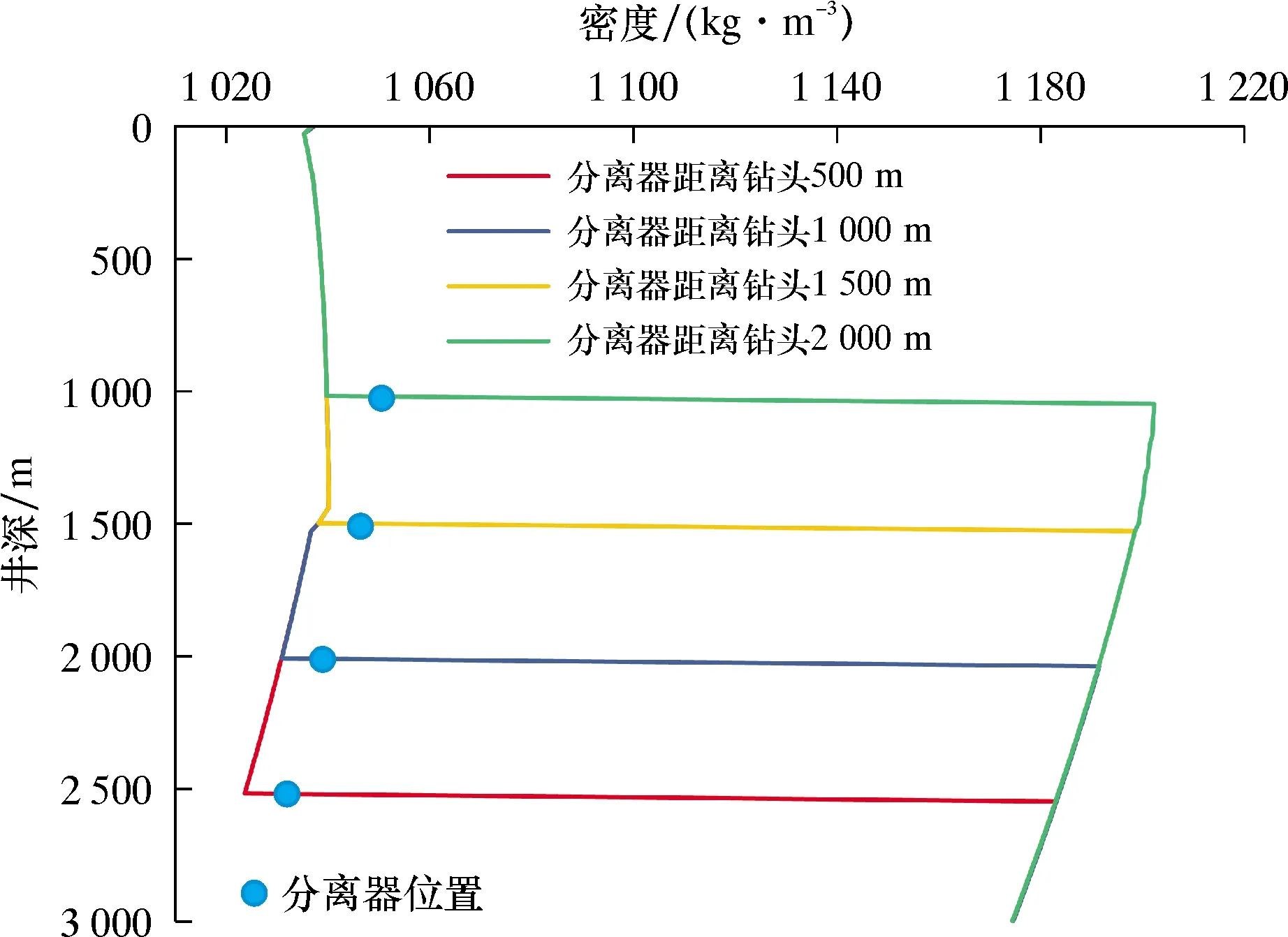
从过滤分离器的分离口分离出的混合流体会与下部环空中上返的钻井液产生汇流,从而在分离口附近的环空区域产生一定的压力波动[12]。分离过程引起的压力波动物理模型如图7所示。图7中,a-b-d-c-a为控制体,并建立如图7所示的坐标系,径向为x方向,轴向为y方向。垂直于坐标轴为z方向,长度为单位长度。上返的钻井液为主流,沿着y轴正向流动。而分离出的钻井液与空心球的混合流体称为射流,沿着x轴正向流动。主流与射流分别从ac与ab两侧进入控制体。两者在控制体内混合后经截面b′d′流出。h为射流产生的入侵横流对主流的在径向上的最大影响深度,L为控制体径向长度,h 1—水泥环;2—套管;3—钻井液与空心球;4—过滤分离器;5—钻头;6—地层。 分离口处无射流时相同位置的压力为pj,ab边界的面积为Aab,射流速度与流量分别为vj和Qj,bb′边界的面积为Abb′。因为该边界为微元体流动的增量,其长度对整个井筒长度几乎可以忽略不计,所以假设此处的压力与分离出口的压力值相同为pj。径向射流与垂直上返的钻井液在控制体内部会产生摩擦阻力,故在径向上对控制体建立动量守恒方程,于是有: ρLQjvj=p(Aab+Abb′) (1) 因为在z方向上控制体的厚度为dx,由此可知Aab=L1dx,Abb′=L2dx。将其代入式(1)中可以得到单个喷射口的动量方程,如式(2)所示,并可求得喷射口相同深度处的环空压力,如式(3)所示。 (2) (3) 由式(3)可知,等式左边为控制体右边界处压力,等式右侧第一项为无射流时控制体右边界处的压力,而等式右侧第二项则为射流引起的压力波动的增量值。因为微元体的移动量L2相对于L几乎可以忽略不计,并且该微小流动远小于射流产生的压力波动,所以略去L2项,简化为式(4)。 (4) 式(3)右边第二项即为过滤分离器分离过程所引起的环空压力波动,并将Blasius提出的范宁摩阻系数f,如式(5)所示[14-15],混合流体的密度如式(6)所示,代入可以得到如式(7)所示的波动压力数学模型。 (5) ρL=ρs(ψε)+ρm(1-ψε) (6) (7) 在注空心球双梯度钻井过程中,可以通过动态调节注入空心球的体积分数和钻井液的排量或者动态改变分离器的位置等实现对井筒压力的动态调节。如果钻井液的排量与空心球的体积分数随时间呈动态变化,在t时刻钻井液的排量为Qm(t),空心球的体积分数为α(t),空心球的排量为Qs(t),故可以得到t时刻空心球与钻井液的混合流体的排量,如式(8)所示。空心球的体积分数如式(9)所示。 Q(t)=Qm(t)+Qs(t) (8) α(t)=Qs(t)/[Qs(t)+Qm(t)] (9) 联立式(8)和式(9),可以得到t时刻的空心球注入排量: Qs(t)=α(t)Qm(t)/[1-α(t)] (10) 钻井液的排量与空心球的体积分数随时间的变化率可以表示为: (11) 若Qm0和α0分别为钻井液与空心球的初始排量与初始空心球体积分数,故可得t时刻钻井液的排量以及空心球的体积分数与其变化率之间的关系,如(12)式所示: (12) 从而可以得到经过时间t后,注入的混合流体的总体积如式(13)所示。再将式(10)与(12)代入式(13)中,并进一步整理可以得到式(14)。 (13) (14) 而t时刻混合流体的密度可以表示为: (15) 然后将式(10)与式(12)代入式(15)中,可以得到t时刻混合流体的密度: ρ(t)=[1-(α0+αst)]ρm+(α0+αst)ρs (16) 以过滤分离器为界,上部环空中的流体为空心球与钻井液的轻质混合流体,而下部环空中近似为原钻井液。由于在钻进过程中会不断产生岩屑,岩屑与钻井液混合会使钻井液的密度发生变化,进一步地影响井筒压力,所以还需要对岩屑产生的附加密度增量进行计算。根据岩屑的迟到时间(式(17)),可以计算在该段时间内产生的岩屑质量,如式(18)所示。 t=Va/Q(t) (17) (18) 假设产生的岩屑均匀分布在钻井液中,则岩屑产生的附加密度增量为: (19) 在钻进过程中,分离器的位置处于动态变化状态,随着钻进时间的延长,分离器距离井口的距离也逐渐增加,从而使得轻质钻井液段与重质钻井液段的液柱长度也呈现动态变化。 根据如图8所示的物理模型,如果以海底泥线为钻进初始时刻,则分离器距离井口的距离以及实时井深随时间的变化分别如式(20)和式(21)所示。 图8 深水双梯度钻井井筒压力计算物理模型 HL(t)=H0+wt (20) L*(t)=Lw+wt-h0 (21) 则环空压力为上部环空中的轻质流体、下部环空中的重质钻井液(相对轻质流体而言)的静液柱压力以及环空中的循环压耗之和,如式(22)所示: [ρm+Δρr(t)]gHw(t)+ΔpfwHw(t)+3pB (22) 从而可以得到随钻井底压力为: [L*(t)-h0]+[ρm+Δρr(t)]gh0+ Δpfwh0+3pB (23) 根据上述推导的双梯度钻井随钻井底压力的数学模型,结合南海某区块的钻井数据进行计算。其中部分数据如下[16-20]:水深为1 500 m,入口温度为15 ℃,地表温度为20 ℃,混合流体的初始排量为10 m3/h,地温梯度为0.25 ℃;钻井液初始密度为1 200 kg/m3,比热容为3 900 J/(kg·K),导热系数为1.73 W/(m·K);海水密度为1 050 kg/m3,比热容为4 130 J/(kg·K),导热系数为0.65;空心球密度为600 kg/m3,比热容为750 J/(kg·K),导热系数为0.47 W/(m·K);选择过滤分离器的分离效率为98.5%。 3.2.1 空心球体积分数的变化率 当其他条件不变时,研究了空心球不同体积分数变化率对随钻井底压力以及环空中流体密度的影响,结果如图9和图10所示。 图9 空心球不同体积分数时随钻井底压力的变化曲线 图10 空心球不同体积分数时流体密度的变化曲线 由图9可知:当空心球体积分数变化率一定时,随钻井底压力随井深不断增加;而当空心球体积分数的变化率不断增加时,相同井深处随钻井底压力逐渐减小。因为随着空心球体积分数的变化率不断增加时,在相同时间内进入到上部环空中的空心球含量增加,从而降低了上部环空中混合流体的密度,使得相同井深位置随钻井底压力不断减小。同时以分离器为分界,由于上、下环空中存在密度差,所以随钻井底压力存在明显的拐点。 由图10可知,随着空心球体积分数的变化率逐渐增加,在相同井深位置,上部环空中混合流体的密度不断减小,而下部环空中流体的密度基本不变,所以上、下环空中的密度曲线在分离器位置存在突变点。因此,通过动态调节空心球的体积分数的变化率,可以灵活调节上部环空中混合流体的密度以及液柱长度,从而进一步地实现对随钻井底压力的动态调节。 3.2.2 钻进时间 图11和图12分别为钻进时间对环空中流体的密度以及随钻井底压力的影响规律。由图11和图12可知,随着钻进时间的延长,实时井深不断增加,同时分离器距离井口的距离不断增加,从而使轻质钻井液段的液柱长度不断增加。由于空心球的体积分数随着钻进时间呈动态变化,故随着钻进时间的延长,上部环空中的空心球的体积分数逐渐增加,于是在相同井深位置上部环空中的混合流体密度显著减小,同样在分离器位置密度存在突变点;而随着钻进时间的延长,在相同井深位置的随钻井底压力逐渐减小。 图11 不同钻进时间时流体密度的变化曲线 图12 不同钻进时间时随钻井底压力的变化曲线 3.2.3 机械钻速 图13和图14分别为机械钻速对随钻井底压力与环空中流体密度的影响。由图13和图14可以看出,在相同时间内,随着机械钻速的增加,实时井深逐渐增加。因为钻进时间相同,所以动态注入上部环空中空心球的体积分数保持不变,故在相同井深位置,上部环空中混合流体的密度基本相同,随钻井底压力也基本保持不变。 图13 不同机械钻速时随钻井底压力的变化曲线 图14 不同机械钻速时流体密度的变化曲线 3.2.4 分离器位置 图15和图16分别为动态调节过滤分离器与钻头的距离时,随钻井底压力与环空中流体密度的变化规律。由图15和图16可知,由于钻进时间相同,所以动态注入上部环空中空心球的体积分数相同,而随着过滤分离器与钻头的距离不断增加,上部环空中轻质钻井液段的液柱长度不断减小,而重质钻井液段的液柱长度不断增加,所以随钻井底压力逐渐增大。 图15 分离器距离钻头不同位置时随钻井底压力的变化曲线 图16 分离器距离钻头不同位置时流体密度的变化曲线 本文通过设计过滤分离器显著提升了分离效率,并通过数值模拟与室内试验进行了验证。然后在考虑波动压力影响的条件下,建立了双梯度钻井随钻井底压力预测模型。最后对不同影响条件下的井筒压力动态变化规律进行了数值计算,并得到如下结论: (1)通过数值模拟与室内试验验证了过滤分离器可以实现高效分离,最大分离效率可以达到98.5%。基于该分离器,建立了空心球分离过程所产生的波动压力数学模型。该研究不仅实现了对现有技术瓶颈的突破,同时也提升了双梯度钻井随钻井底压力计算模型的精确度。 (2)在考虑波动压力的影响下,建立了双梯度钻井随钻井底压力的数学模型。随钻井底压力在分离器位置存在明显的拐点,而且上、下环空中的钻井液密度分布存在突变。 (3)不考虑空心球体积分数的动态变化以及分离器位置的改变,该模型还可以动态预测不同钻进时间与机械钻速条件下的随钻井底压力。 (4)随钻井底压力与空心球体积分数变化率呈负相关,与分离器距离钻头的位置呈正相关。当改变分离器位置与空心球体积分数的变化率时,可以实现对双梯度钻井随钻井底压力的动态预测。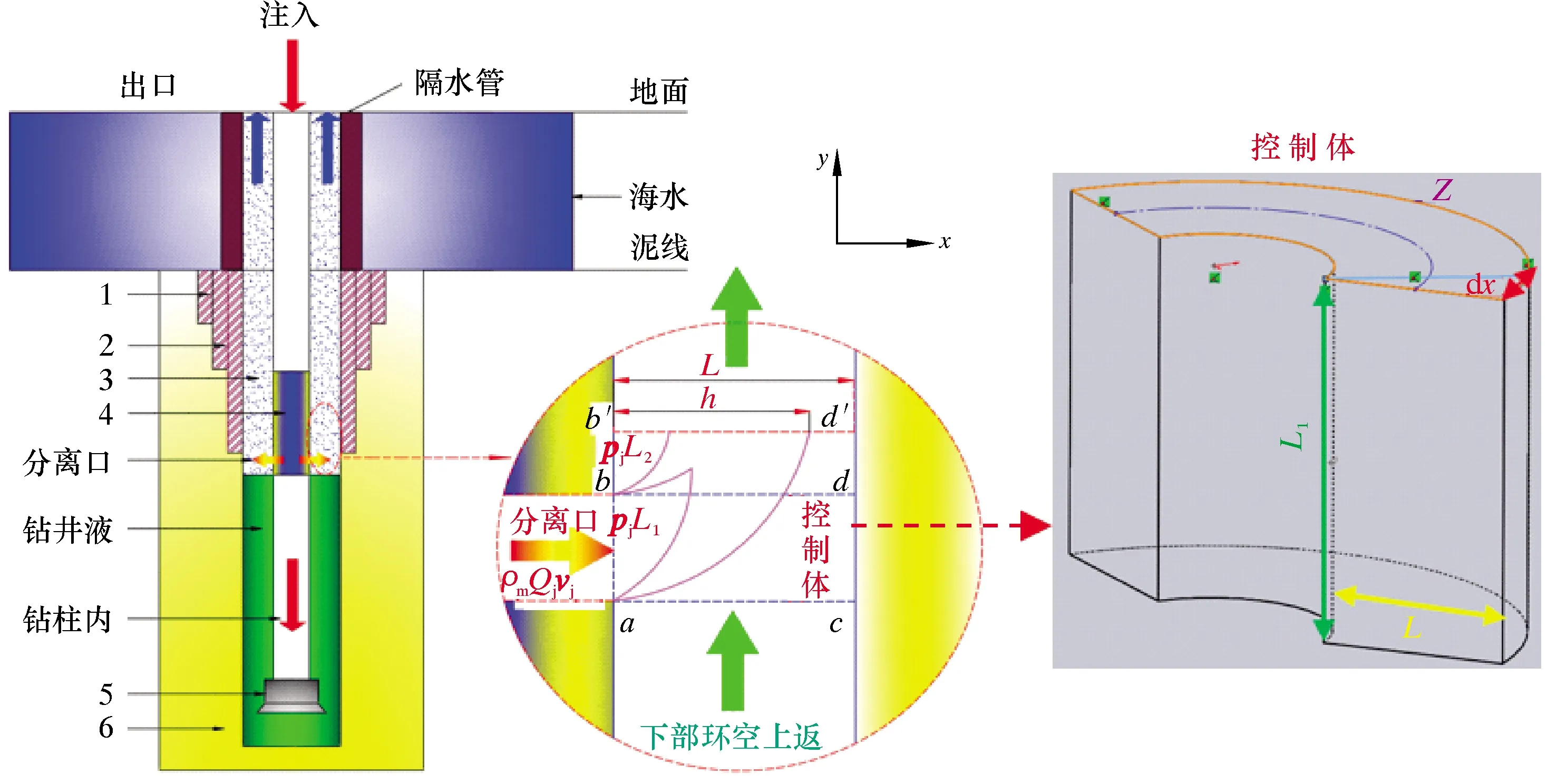

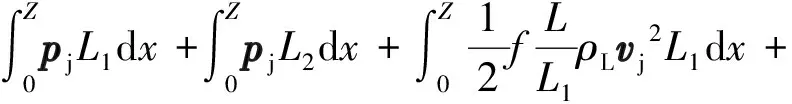


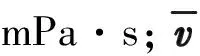
2.2 井筒压力研究





3 算例分析
3.1 基础数据
3.2 随钻井底压力的影响因素分析





4 结 论
