一种基于CPN网络的分布式粒子群优化算法

张振亚，骆丽春，王越，王萍，程红梅

（1.智能建筑与建筑节能安徽省重点实验室，安徽 合肥 230022；2.安徽建筑大学 电子与信息工程学院，安徽 合肥 230601；3.安徽建筑大学 经济与管理学院，安徽 合肥 230601）

关键字：粒子群优化算法；CPN网络；分布式系统；群智能建筑平台

智能建筑指通过将建筑物的结构、系统、服务和管理根据用户的需求进行最优化组合，从而为用户提供一个高效、舒适、便利的人性化建筑环境。智能建筑是集现代科学技术之大成的产物。目前，DCS（Distributed Control System，集散控制系统或者分散控制系统或者分布式计算机控制系统）是智能建筑设计与实现主要采用的控制架构，其基于控制分散、操作和管理集中的基本设计思想，采用多层分级、合作自治的结构形式，其主要特征是它的集中管理和分散控制。PLC（Programmable Logic Controller）、FCS（Fieldbus Control System）技术的发展与成熟丰富了DCS的实践。虽然这种架构可以实现对设备的分布式控制，但是，存在一台或多台主计算机系统组成的中心节点是这种架构的重要特征。不仅数据集中存储在中心节点，系统所有业务单元的集成与数据交换也在中心节点上实 现。基于DCS理念实现的智能建筑管理平台实现时，即使是使用PLC、FCS技术实现了完全的分布控制，依然存在纵向集成条块分割、组网成本高、系统更改扩充变动成本高、用户难以获取整体信息、系统鲁棒性差的典型问题。

针对这些典型问题，国家重点研发计划项目“新型建筑智能化平台系统技术”提出并设计了一种基于无中心、扁平化架构理念的新型智能建筑平台系统：群智能建筑平台系统。该平台系统将建筑空间视作各建筑子空间的组合，而建筑设施（设备）也被视作是重要部件的组合。每个建筑子空间和建筑设备的重要部件都配备一个名称为CPN（Computing Process Node，计算处理节点）的“智能节点”，建筑子空间对应的CPN节点简称空间CPN节点，空间CPN节点之间按照建筑子空间邻接的关系进行连接：空间邻接的空间CPN节点通过RJ45接口使用双绞线直接连接，全部空间CPN节点构成了一个以空间邻接属性为约束的网格；建筑物内，建筑设施（设备）被视作是重要部件对应CPN节点（设备CPN节点）之间按照组成建筑设施/设备各部件在空间中的彼此邻接/邻居关系进行连接：若两个部件在空间上近邻，当且仅当这两个部件中间不存在具有设备CPN节点的部件，则这两个部件的设备CPN节点通过RJ45接口使用双绞线连接；空间CPN网格与设备CPN网络在设备间以空间CPN与设备CPN直连的方式实现互联，形成支撑新型建筑智能化平台系统的基础网络：CPN网络。CPN网络是支撑新型建筑智能化平台系统的基础网络，若将其视作图G，则每个子系统对应的设备CPN网络都是G的子图。对新型（群）建筑智能化平台系统，基于基础网络G可以定义各建筑设施/设备系统对应的CPN子网，如空调系统的CPN子网、供配电系统的CPN子网、安防系统的CPN子网、消防系统的CPN子网 等。

粒子群优化算法是智能建筑应用中使用较多的优化方法。基于CPN网络的群智能建筑平台，无论是设备CPN节点还是空间CPN节点，每个CPN节点都具有信息综合处理与计算、数据存储能力以及与相邻CPN节点进行数据交互的能力。面向群智能建筑平台系统中建筑智能化策略以及建筑节能策略的实现，本文对粒子群优化算法进行了改进，提出了基于CPN节点的粒子群优化算法的分布式实现机制。CPN网络拓扑结构及其构建在第二部分给出，基于CPN网络的粒子群优化算法改进在第三部分给出，第四部分对改进粒子群优化算法的性能进行了实验验证与分析，总结与展望在第五部分给出。

1 CPN网络

CPN是群智能建筑平台构建使用的智能计算节点，无论是空间CPN之间、设备CPN之间还是空间CPN与设备CPN之间，都可以通过RJ45接口使用双绞线直连。每个空间CPN有8个RJ45接口：1个为WAN口，用于通过外部网络/公网与远端的服务器连接，远端的服务器可以提供CPN的初始化、更新以及下载APP等服务；1个为LAN口，既可以用于使用PC/笔记本在本地设置CPN，也可以用于将本地诸如温度、湿度、照度、人数等属性信息上传到本地CPN节点；其它6个邻接接口，用于空间CPN彼此之间的连接（形式上，表示前后左右上下6个方位的空间）。设备CPN在具有与空间CPN一致的RJ45接口的同时，还带有诸如485、232以及其它总线接口用于与设备的连接。图1给出了CPN与CPN网络的示意。

图1（a）描述了CPN的核心功能：逻辑上，一个CPN（智能节点）包括可编程控制器PCT模块、本地存储MD模块、输入模块I、输出模块O等四个模块。其中，可编程控制器PCT模块用于本地的信息处理与控制决策，本地存储MD模块用于存储本地空间的状态数据或者本地设备的状态数据，输入模块I用于PCT模块进行决策时所需外部信息（设备状态信息、空间状态信息等）的获取，输出模块O用于向空间或者设备发布PCT模块进行的决策。为支持智能节点群（CPN网络）构建，一个CPN节点还提供了6个用于其它CPN节点连接的直连端口DP。为简化设计，目前6个直连端口DP在实现时都使用了RJ45接口，而输入模块I、输出模块O实现时使用了RJ45接口和WIFI接口。在部分机电设备专用CPN设计时，输入模块I、输出模块O也提供了对RS485、RS232接口的支持。

图1 CPN与CPN网络示意

如图1（a）示意，相邻的CPN节点通过直连端口使用数据线直连后，全部CPN节点就构成了一个可以CPN网络形式描述的智能节点群落。智能节点群落中，每个智能节点只能通过直连端口与邻居交换信息。这样，一个智能节点就可以通过综合本地输入模块获取的数据、存储在本地的历史数据以及从邻居节点交换获得的信息进行决策，实现对本地空间状态、设备状态的全局（或局部）最优控制。这种最优控制决策形成时，计算力、数据存储不需要汇聚到指定的计算节点，呈现计算无中心、数据无中心的特点，同时，由于智能节点群落中，每个智能节点功能一致，智能节点群落呈现扁平化的特点。此时，若将智能节点群落作为一种新型的群智能建筑平台系统，则无中心、扁平化是这种群智能建筑平台系统最明显的特点。

图1（b）直观地展示了一个使用CPN节点构建的群智能建筑平台系统上CPN节点在建筑空间中的分布情况：空间CPN节点依据所在区域的邻接情况使用直连端口直连，设备CPN节点依据部件的邻接情况使用直连端口直连，设备CPN子网、空间CPN子网在设备间通过直连端口实现了互联。整体上，一个基于CPN的群智能建筑平台系统，其基础计算平台是一套由建筑物内全部CPN节点互联形成的CPN网络。在拓扑结构上，该CPN网络类似于图1（c）示意的由CPN节点通过局部直连而形成的CPN网格。

基于CPN的群智能建筑平台系统中，CPN节点上运行的决策是群智能建筑平台系统中的APP。每个CPN节点上可以同时运行支撑群智能建筑平台系统全部APP，而这些APP在一个CPN节点上，可以通过轮转方式周期性地执行，也可以在触发条件满足时被执行。

显然，根据图1（c）示意的CPN网络的拓扑，在CPN网络中，空间不相邻的两个CPN节点之间不会通过直连端口直接连接。可以证明，对任意一对不直连的CPN，一个CPN节点上的数据，可以也必须通过有限次数的转发传递到另一个CPN。

2 基于CPN网络的改进粒子群优化算法

群智能建筑平台系统的CPN网络中，无论是设备CPN节点还是空间CPN节点，每个CPN节点都具有信息综合处理与计算、数据存储能力以及与相邻CPN节点进行数据交互的能力。基于CPN网络实现粒子群优化算法时，可以在每个CPN节点中设置若干个粒子，每个CPN节点中执行本地策略以更新本地每个粒子的速度和位置。

对粒子群优化算法中，设t时刻位置在x（t）、速度为v（t）的粒子，则t+1时刻，其位置x（t+1）与速度v（t+1）一般按照式（1）、（2）规定的策略更新。式（1）中，

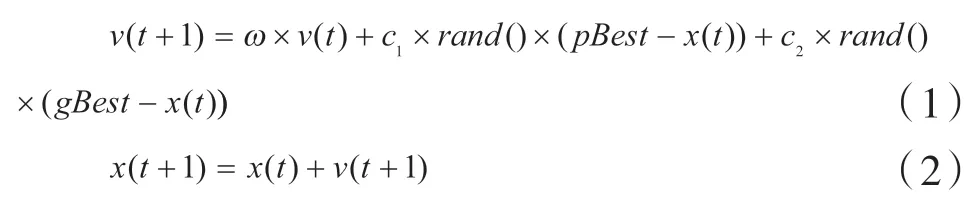
ω

是惯性因子，

c

、

c

是学习因子，rand（）是随机数，

pBest

是粒子的历史最优位置，而

gBest

为全部粒子的历史最优位置。由于在群智能建筑平台系统中，粒子群优化算法的全部粒子分布在CPN网络中的每个CPN节点中，而每个CPN节点只能够与其邻居节点交换数据，这使得遍历网络中每个CPN节点以获得全部粒子历史最优位置操作只能通过迭代查询的方式实现，这不仅使得获取当前时刻全部粒子历史最优位置的操作代价高昂，而且由于迭代查询显著增加的消息转发请求也将额外消耗网络的资源，将对CPN网络的性能产生负面影响。因此，在CPN网络中实现粒子群优化算法时，直接使用式（1）、（2）规定的策略更新每个粒子下一时刻的速度和位置的做法有待改进。对基于CPN网络的分布式PSO算法，设：1）每个CPN节点中有若干个粒子；2）对任一CPN节点，记

gBestL

是该CPN节点中全部粒子的历史最优位置；3）对某个CPN节点，若其有

m

个邻居CPN节点，记

gBestLi

是其第

i

个邻居节点中全部粒子的最优位置，规定

gBestA

如式（3）。则对基于CPN网络的分布式PSO算法，某个CPN节点中任意粒子，若

t

时刻其位置为

x

（

t

）、速度为

v

（

t

），则其在

t

+1时刻的速度

v

（

t

+1）与位置

x

（

t

+1）可以依据式（4）、（2）确定。称式（3）是基于CPN网络的分布式PSO算法的数据交换策略，而式（4）、（2）是基于CPN网络的分布式PSO算法中粒子位置的更新策略。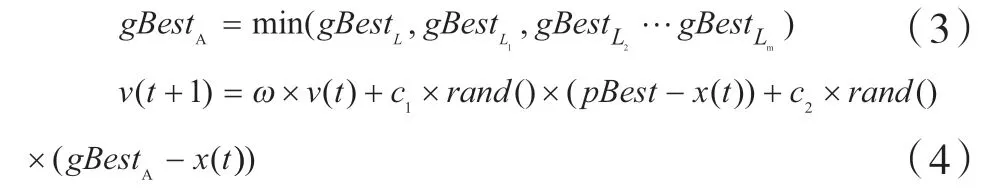

算法1：基于CPN网络的分布式粒子群优化算法输入：本地粒子数n，学习因子c1、c2，惯性因子ω，最大迭代次数maxN，适应度函数fun输出：最优个体的位置1）初始化每个本地粒子的速度与位置2）对本地的每个粒子，将其初始位置作为其历史最优位置的初始值3）依据本地每个粒子的最优位置，计算本地全部粒子最优位置gBestL 4）k=1；5）while k<=maxN 6） 获取每个邻居节点的历史最优位置gBestLi，i=1，2…m 7） 依据式（3）计算gBestA 8） for each 本地粒子9） 依据式（4）和式（2）更新速度和位置10） 使用适应度函数fun计算位置更新后粒子的适应度值11） 若新位置的适应度值较粒子历史最佳适应度的值更 小，将粒子历史最优位置设置为粒子的当前位置12） 更新本地全部粒子最优位置gBestL 13） k=k+1 14）输出gBestL

算法1中，以粒子的适应度值评估每个粒子位置的优劣：适应度值越小，粒子位置越优越；粒子的适应度值用适应度函数

fun

计算，

fun

函数以粒子的位置为自变量。设

gBest

是k时刻CPN网络中全部CPN节点全部粒子的全局最优位置，则对CPN网络中任意CPN节 点

fun

（

gBestL

）≥

fun

（

gBestA

）≥

fun

（

gBest

）。因此，类似式（1）、（2）规定的粒子群优化算法中粒子速度与位置更新，对任意一个CPN节点中的粒子群中的粒子使用式（4）、（2）更新速度和位置，该CPN节点中的粒子群中粒子位置收敛。进一步，对全部CPN节点中的粒子群，虽然

gBest

可能不出现在每个CPN节点的粒子群中，但依据CPN网络中CPN节点的连接特性和式（3）可知：由于任意两个CPN节点在CPN网络中有限步可达，故全局最优位置

gBest

可以经过有限次迭代传递到CPN网络中每个CPN节点上的粒子群（极端情况：CPN网络中全部m个CPN节点线性排列，设第一个CPN节点是A，最后一个节点是B。若最优位置

gBest

是A节点粒子群中的局部最优位置，则至多经过m-1次迭代，B节点上的局部最优位置优于m-1次迭代前A节点的粒子群的局部最优位置，即优于m-1次迭代前的全局最优位置）。显然，式（3）规定的数据交换策略可以使全局最优位置

gBest

在CPN网络中每个CPN节点上传播，而全局最优位置gBest可以传递到CPN网络中每个CPN节点，意味着CPN网络中每个CPN节点上的粒子群本地局部历史位置

gBestL

距全局最优位置有限步可达，表现为当算法1运行结束时，每个CPN节点中粒子群的本地局部历史位置

gBestL

的适应度值差异较小。

3 实验结果与分析

基于观察数据拟合数据的变化规律是建筑智能化和建筑节能应用实现时常见数据处理任务。为测试算法1的性能，实验设定的数据拟合任务：已知样本数据集

D

={（

x

，

d

）|

i

=1，2，…63}，

d

=sin（

x

），

x

=-3.1416+（i-1）*0.1，用一个有1个输入神经元、含有6个隐层神经元的单隐层前向神经网络net拟合生成该样本数据集的生成函数拟。显然，被拟合函数为

y

=sin（

x

），∀

x

∈[

-ππ

]。

设

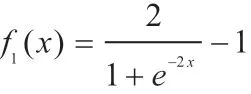
W

、

U

、

B

、

B

取值确定，以样本数据集

D

中的

x

为输入时net的输出为

y

，规定适应度函数

fitness

（）如式（5）。显然，

fitness

的值越小，net对函数

y

=sin（

x

）的拟合性能越好。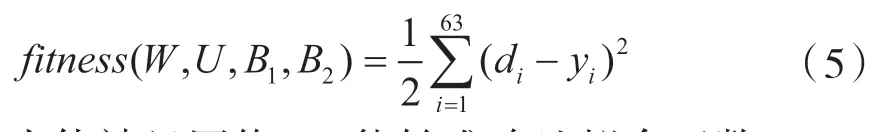

为使神经网络net能够准确地拟合函数

y

=sin（

x

），需要优化

W

、

U

、

B

、

B

的取值。实验通过使用算法1优化

W

、

U

、

B

、

B

的取值对算法1的性能进行了测试。

实验首先使用依据式（1）、（2）实现了非分布式粒子群优化算法（以下简称算法2）。实验中，算法2在Matlab 2016实现。算法2在实现时，记录每运行1遍算法使用的时间。

由于算法2在实现时，粒子的初始位置、初始速度以及式（1）规定的粒子速度更新策略都使用了随机数，可以预期使用粒子群优化算法训练神经网络net关于目标函数的拟合精度、训练时间存在波动。对所实现的算法2，以粒子数400、学习因子c1、c2均取值为2、惯性因子ω=0.8为输入，重复执行20遍。表1给出了迭代次数为1000时，算法2训练前向神经网络net拟合目标函数的性能。显然，前向神经网络net的训练时间比较稳定。当算法2终止运行、神经网络net训练完成时，net对目标函数的拟合精度最佳可以达到10数量级，拟合精度均值的数量级也可以达到10。考虑到拟合精度中位值的数量级达到10，显然绝大多数情况下，算法获得的对

W

、

U

、

B

、

B

等参数的估计可以使前向神经网络net较好地拟合目标函数。表2给出了迭代次数为2000时，算法2训练前向神经网络net拟合目标函数的性能。显然就拟合精度而言，结论与根据表1的结论一致。同时，注意到表1中，拟合精度均值为0.0038，而标准差为0.0083，这表明使用算法2训练前向神经网络net拟合目标函数时拟合精度存在着显著地波动。拟合精度的均值、稳定性的提升可以通过增加迭代次数实现：在其他参数不变的情况下，迭代次数从1000增加到2000，表2中拟合精度的均值以及标准差信息表明，通过增加迭代次数的方法提升拟合精度的均值、稳定性可行。表2中的数据为算法2以粒子数400、学习因子c1、c2均取值为2、惯性因子ω=0.8为输入，重复执行20遍时采集。对比表1、表2中的算法运行时间，显然，增加迭代次数将会显著增加训练神经网络net的时间，这意味着应用中要在提升前向神经网络net的拟合精度的性能和训练时间两者之间进行折中。

表1 非分布式粒子群优化算法的性能 （粒子数：400、c1=2、c2=2、ω=0.8、1000次迭代、20遍）

表2 非分布式粒子群优化算法的性能 （粒子数：400、c1=2、c2=2、ω=0.8、2000次迭代、20遍）

对算法1，实验使用的CPN网络拓扑如图2所示。图2中，每个灰色圆点表示一个CPN节点，边表示了CPN节点的连接情况。实验中，全部CPN节点4行5列形式排列，共20个CPN节点，一个CPN节点表示一个建筑空间分区或建筑设备组件（以下统称为分区）。每个CPN节点只能够向直接连接的CPN节点发送查询请求，任意两个不直接连接的CPN节点不能直接交换数据。

图2 CPN网络拓扑结构

实验中，算法1在Matlab 2016实现。算法1使用分区结构仿真CPN节点，各CPN分区串行调度，所记录的运行时间为全部CPN分区被调度完成后算法1的运行总时间。

图3给出了对全部20个CPN节点，均设置粒子数为20、c1=2、c2=2、ω=0.8、迭代次数为1000时，使用算法1训练前向神经网络net拟合目标函数时拟合精度的分布情况：最小值为5.1218e-04，最大值为5.8891e-04，均值为5.3154e-04，中位值为5.2618e-04，标准差为2.0246e-05。显然，相较算法2（非分布式粒子群优化算法），在迭代次数、学习因子、总粒子数、惯性因子一致的前提下，算法1（分布式粒子群优化算法）拟合精度性能更高且更稳定。全部20个CPN执行1次算法一共耗时146.0983秒，考虑到在CPN部署后全部20个CPN分区的计算任务将并行执行，在不考虑通信开销的前提下，算法1可以在146.0983/20=7.3049秒左右完成；相较于表1中给出的算法2的平均运行时间（102.0537秒）和表2中给出的算法2的平均运行时间（202.6170秒），算法1的执行速度更优。

图3 算法1的拟合精度分布 （20CPN、20粒子/CPN、c1=2、c2=2、ω=0.8、1000次迭代）

为测试每个CPN上的粒子数以及迭代次数对算法1性能的影响，实验固定每个CPN中粒子数为10、c1=2、c2=2、ω=0.8，算法1将迭代次数依次从1000增加到20000，每次增加1000操作，使用算法1训练前向神经网络net拟合目标函数的拟合精度情况与总耗时由表3给出。对比表1、表2、表3，就使用粒子群优化算法训练前向神经网络拟合目标函数而言，算法1可以使用较少的粒子数以增加迭代次数的方式取得优于算法2的性能。而由于算法1是基于CPN网络分布式执行，相较于非分布式粒子群优化算法迭代次数同等的增加，单个CPN中因迭代次数增加导致的时间消耗增幅并不显著。

表3 算法1的性能（20CPN、10粒子/CPN、c1=2、c2=2、ω=0.8）

观察表3中最小值、最大值、均值和方差两列数据还可以发现，每个CPN使用算法1获得的最优解在拟合精度上具有类似的性能，差异小。算法1是粒子群优化算法基于CPN网络的分布式实现。从表3可以发现，在算法1的一次运行结束后，每个CPN节点中本地历史最优位置的适应度值波动不大，这样，在算法1执行结束后，本地的最优解可以作为全局最优解的逼近。

4 总结与研究展望

针对主流智能建筑管理平台的纵向集成条块分割、组网成本高、系统更改扩充变动成本高、用户难以获取整体信息、系统鲁棒性差的现状，基于无中心、扁平化理念，新型的群建筑智能化平台使用CPN网络，采用与建筑空间拓扑/建筑机电设备系统拓扑一致（近似）的网状拓扑结构的方式破解了智能建筑不同子系统相对独立产生的条块分割问题。基于CPN网络面向建筑智能化应用和建筑节能应用需求，和基于CPN网络的拓扑结构，为实现分布式粒子群优化算法，本文设计了本地CPN节点与邻居CPN节点的数据交换机制，提出了融合本地最优解和邻居最优解的基于区域最优解的粒子位置更新策略。实验表明，无论是从拟合精度还是从消耗时间角度看，基于CPN网络的分布式粒子群优化算法具有更高的性能。

本文设计与实现的基于CPN网络的分布式粒子群优化算法是CPN网络中粒子群优化算法实现的一种有效架构。结合特定的应用，如区域内建筑设备控制、传感器故障检测、人员分布等，探索该粒子群优化算法实现架构在新型的群智能建筑平台中的应用值得关注。

事实上，若将每个CPN的分区上运行的算法1视作算法2的改进，则基于CPN的分布式粒子群优化算法（算法1）的一次运行可以获得若干个（等于CPN网络中CPN节点数量）算法2的解，由于每个CPN节点上算法1的局部最优解在拟合精度上具有类似的性能，因此可以将每个CPN节点上算法1的局部最优解是若干个算法2获得最优解的集成，这意味着算法1是一种基于算法2的集成学习方法的实现。进一步，群智能建筑平台中，基于CPN网络的集成决策机制也是值得深入地探索。