钛合金材料页轮磨抛材料去除深度模型*
2022-01-15胡智杰曹诗宇黄文健吴超群
胡智杰, 曹诗宇, 黄文健, 吴超群,2
(1.武汉理工大学 机电工程学院, 武汉430070) (2.华中科技大学, 数字制造装备与技术国家重点实验室, 武汉 430074)
随着科学技术的不断发展,钛合金材料在航空、航天及军用设备中的应用越来越广泛,已成为仅次于钢铁、铝合金的第三大金属合金材料。与钢铁和铝合金相比,钛合金材料具有强度高、比质量轻的优点,能满足航空航天材料的需求,具有极大的应用前景[1]。
为提高钛合金零部件的表面质量和使用寿命,在初加工后,对零部件表面进行磨抛处理是不可缺少的一步。比如:由钛合金材料铸造的航空发动机机匣,在经过浇冒口清理、初打磨、喷砂等一系列工艺后,需要对其关键部位进行磨抛处理,以提高表面质量[2]。但由于钛合金材料本身的硬度高、比强度大、热导率低等特性,其磨抛过程极为困难,磨抛深度难以控制,在加工过程中产生了大量的原材料损耗。国内外学者针对上述问题进行了大量研究,并建立了对应的理论模型。
RAFIEIAN等[3]对机器人砂轮磨抛过程的振动动力学进行研究,并通过实验建立对应的磨削力模型。该模型可以精确地计算出砂轮将材料去除到目标深度时所需的磨削力,为研究机器人磨抛操作中材料去除率的控制提供了一种新策略。张阳[4]基于Preston经验方程,建立针对鼓型接触轮砂带磨削的材料去除模型,分析接触轮硬度、半径、法向磨抛力及工件曲率半径对接触压强的影响,为磨抛加工提供了理论参考。WANG等[5]基于幂级数法的弹性力学方法,建立带张力导致接触轮变形的模型,并用有限元验证模型的有效性,通过该模型可准确预测磨削时的深度。针对砂带张紧力引起的接触轮变形问题,刘斐等[6]建立一种机器人砂带磨削深度仿真和预测模型,为精确磨削复杂曲面提供了理论指导。
目前常用的磨抛工具主要有砂轮、砂带和页轮。在材料磨削加工去除深度的理论建模研究中,多是针对砂轮、砂带磨抛材料的去除过程,而对页轮磨抛进行建模的几乎没有。在实际磨抛钛合金机匣时,页轮具有砂带的柔性磨抛、加工表面质量好、尺寸小、适用范围广的优点[7],是主要的磨抛工具。为解决页轮磨抛时去除深度难以控制的问题,满足实际生产的需求,对钛合金材料在页轮磨抛中的去除深度模型进行全面、深入的研究是必要的。
因此,通过Preston方程,将整个页轮磨抛过程简化为材料去除深度与时间之间的线性关系,并结合Hertz接触理论和弹性接触力学理论中的线接触变形,得到接触压强大小的分布情况,再结合接触压强与预压量的关系,建立材料去除深度与页轮线速度vs、预压量ap以及进给速度vf的理论模型。在试验过程中,将这3个加工参数作为影响因素,运用机器人完成钛合金材料的磨抛试验,确定模型的常数,揭示磨抛工艺参数对磨抛深度的影响趋势。
1 页轮磨抛材料去除深度模型
1.1 单位路径的材料去除深度
图1为页轮磨抛过程的示意图。页轮由轮基和叶片黏结而成,主轴带动页轮,以线速度vs旋转,在指定的预压量ap下,以进给速度vf进行磨抛加工。在此过程中,页轮对工件表面产生Fn的正压力,并且页轮上的页片不断旋转,摩擦工件表面,从而产生摩擦力Ff。由于页片具有弹性,磨粒的切削刃磨抛去除材料的过程大致可以分为挤压划擦、耕犁、切削等3个阶段。初始阶段(划擦),页片的弹性变形使磨粒切削刃接触工件表面较少,去除深度小;随着接触压力和磨抛时间的增加,切削刃逐渐钝化,并更多地接触到工件表面,使接触区域由弹性变形转化为塑性变形(耕犁),最终去除工件表面材料(切削),完成工件表面的磨抛加工。在实际磨抛钛合金机匣的过程中,考虑到页轮的曲率半径远远小于钛合金机匣的磨抛面,可将该磨抛过程视为页轮与工件平面接触的过程。
在磨削加工中,Preston方程被广泛用于分析磨抛过程。通过Preston方程,将整个页轮磨抛过程简化为材料去除深度与时间之间的线性关系[4,8]:
(1)
式中:dH为dT时间段内的材料去除深度;p为接触点的压强;vr为磨抛工具与工件的相对速度;Kp为比例常数。
将公式(1)推导到单位路径dl上:
(2)

(3)
1.2 接触区域压强与预压量的关系
假设接触表面光滑,磨抛工具和工件为弹性体材质,忽略动摩擦的影响,抛光点的接触压强p服从Hertz分布,则工件表面的磨抛过程可以看作是Hertz接触中的圆柱与平面接触[9]。
图2为页轮磨抛平面的接触区域压强分布,W、2b分别为接触区域的长度、宽度。接触区域最大压强pm位于x轴上,接触压强p服从赫兹分布,则:
(4)
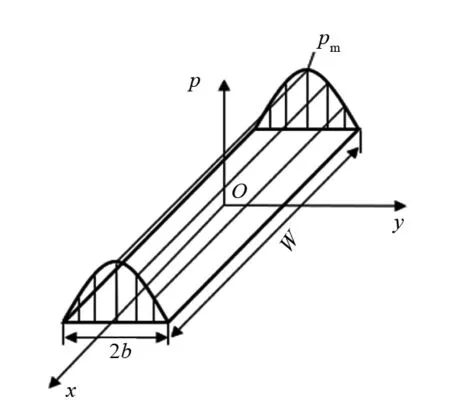
图2 页轮磨抛平面接触区域压强分布
在图2的整个矩形接触区域对式(4)进行定积分,可得到磨抛正压力Fn的推导公式:
(5)
由弹性接触力学理论中的线接触变形计算可知[10-11],正压力Fn与接触区域半宽b的关系式为:
(6)
其中:
(7)
(8)

因为磨抛表面为平面,因而:
(9)

(10)

(11)
1.3 材料去除深度模型的建立
根据式(3),以b为边界条件,对接触区域积分,得到磨抛平面深度计算表达式:
(12)
最后,结合式(11)、式(12),化简后得到页轮磨抛平面的材料去除深度模型:
(13)
(14)
线速度vs由进给速度vf和相对速度vr组成,由于进给速度vf远小于相对速度vr,因此,可忽略进给速度的影响,取相对速度vr为工具的线速度vs,所以:
(15)
从式(15)中可以得到页轮磨抛平面工件时的主要工艺参数对材料去除的影响规律:材料去除深度与页轮线速度vs、预压量ap呈正相关关系,与进给速度vf呈负相关关系。由于材料去除系数K是由进给速度vf、线速度vs和预压量ap之外的其他因素决定,根据Preston方程原理,页轮的材料、页片数量等次要因素对材料去除深度的影响都通过材料去除系数K来表示。
2 试验
2.1 试验平台搭建
搭建的试验平台如图3所示,该平台主要由库卡机器人(型号KR60-3)、电主轴法兰、电主轴(振宇TDK93X82-2.2)、页轮、钛合金工件(TC4)、工装夹具组成。

图3 钛合金材料磨抛试验平台
选用150 mm×80 mm×10 mm的TC4钛合金工件作为试验对象。针对钛合金材料的加工特点,应选用硬度高、稳定性好,不易黏附钛合金材料的页轮[12-13]。因此,选用碳化硅磨粒的页轮,磨粒平均颗粒尺寸为124 μm(粒度代号为F120),页片尺寸为19 mm×25 mm, 轮心直径d为22 mm,芯轴柄直径为6 mm,页片数目为80。
2.2 试验方案设计
为得到去除系数K的具体值,验证磨抛材料去除深度模型的准确性,需要对页轮线速度vs、进给速度vf及预压量ap等因素进行试验分析。因此,将页轮线速度vs、进给速度vf及预压量ap作为试验的3个因素,设计正交试验和单因素试验。
在正交试验和单因素试验前进行大量磨抛试验,选择交互作用较小的1组试验参数作为磨抛试验的基准参数:页轮线速度vs=10 m/s、进给速度vf=10 mm/s及预压量ap=1.5 mm。
参考磨抛基准参数,设计3因素4水平试验,试验的因素和水平如表1所示。

表1 试验因素和水平
3 结果及讨论
3.1 正交试验及单因素试验结果
表2为正交试验的页轮磨抛去除深度变化的试验结果,该试验数据主要用来推导计算磨抛材料去除深度模型的去除系数的值和分析模型中各参数对页轮磨抛去除深度的影响。

表2 正交试验的页轮磨抛去除深度变化的试验结果
由表2可知:页轮进给速度、页轮线速度、预压量参数下的平均极差分别为0.109、0.108、0.098,各参数对材料去除深度的影响程度基本相当。
表3为单因素试验的工件厚度变化的试验结果,该试验主要目的是验证理论推导的磨抛去除深度模型的准确性。

表3 单因素试验的页轮磨抛工件去除深度变化结果
3.2 磨抛过程中去除系数确定
对机器人页轮磨抛正交试验的工件厚度变化结果进行分析。将式(15)化为:
(16)
根据式(16),对表2中的试验数据进行分析计算,得到去除系数K的试验数值,绘制y(即Hvf)与x(即vsap)的关系曲线,并对曲线进行线性拟合。为了得到更好的模型,对试验数据进行优化剔除,图4为剔除表2中L9、L10、L13、L14数据后的去除系数K的拟合直线图,拟合后的直线表达式为:y=3.013×10-5x-2.233×10-8,则去除系数K=3.013×10-5。

图4 去除系数K的拟合直线
3.3 磨抛去除深度模型试验验证
将去除系数K代入页轮磨抛平面的材料去除深度模型,得到的理论数据与表3的试验数据对比结果如图5所示。

(a)H和ap的关系Relationship between H and ap(b)H和vf的关系Relationship between H and vf(c)H和vs关系Relationship between H and vs图5 各磨抛参数下最大材料去除深度仿真与试验曲线对比图Fig. 5 Comparison of simulation and experimentalcurves of maximum material removal depth undervarious grinding parameters
如图5a所示:材料去除深度随预压量的增大而增大。这是由于预压量增大,页轮正压力增大,磨粒切削刃与工件的接触增多,材料去除深度增大。
如图5b所示:材料去除深度随进给速度的增大而减小。这是因为随着进给速度增大,单位面积的工件磨削更少,从而材料去除深度减小。但当进给速度较低(vf=2 mm/s)时, 单位时间内,页轮页片磨削次数增多,页轮磨损严重,从而导致实际的材料去除深度远小于理论值。
如图5c所示:材料去除深度随页轮线速度的增大而增大。这是因为,随着线速度增大,单位面积的工件会磨削更多,从而材料去除深度增大。
对理论数据与试验数据进行整体分析可知,当排除页轮进给速度为2 mm/s的数据时,采用平均相对误差方式,对试验与预测模型的结果进行评价,计算方法如下:
(17)
式中:N取12。计算得到试验和模型预测结果的平均相对误差为6.25%。因此,可以认为页轮磨抛材料去除深度模型是准确的。
4 结论
通过分析工业机器人带动页轮磨抛钛合金材料的过程,基于Preston方程和Hertz接触理论构建页轮磨抛平面时的材料去除深度模型,并采用正交试验和单因素试验对页轮的磨抛参数进行研究,得出:
(1)材料去除深度与预压量和页轮线速度成正比,与页轮进给速度成反比。页轮进给速度、页轮线速度、预压量参数下的平均极差分别为0.109、0.108、0.098,各参数对材料去除深度的影响程度基本相当。
(2)模型预测结果与试验结果具有较好的一致性,平均相对误差为6.25%,验证了模型的准确性及模型相关假设的合理性。
