基于环境模型优化的机器人磨抛阻抗控制*

王竞航, 彭云峰

(厦门大学 航空航天学院, 福建 厦门361000)

弹性磨具是由磨粒与高分子聚合物结合而成的一种具备良好弹性与磨削性能的磨抛加工工具。与传统磨具相比，弹性磨具对曲率变化大的复杂型面有良好的曲面适应性，在接触时存在一定的退让作用，能够避免刀具和工件的直接刚性接触，有效降低工件表面损伤与划痕。同时，弹性磨具磨粒分布均匀，接触回弹后产生的退让变形使磨具与工件始终接触，提高了复杂曲面工件的磨削效率。但由于弹性磨具的弹性退让与非常量磨损，影响并导致接触压力复杂，造成实际磨抛量与理论磨抛量不一致，使磨抛参数的变化规律很难得到理论认证[1]。

在利用弹性磨具进行磨抛加工的研究上，周龙等[2]研究了聚氨酯磨具的力学性质并建立了单颗磨粒的切削模型，验证了聚氨酯弹性磨具用于精密磨削的可行性。吴晓军等[3]使用弹性球形砂轮进行抛光实验，对切深、进给速度、主轴转速、粒度4个磨削参数对抛光性能的影响进行了研究，获得了多指标参数优化组合。SOORAJ[4]用聚氨酯基弹性砂轮进行超精密磨削，发现由于砂轮法向的弹性变形难以控制，因而使用切削深度控制不如使用切削力控制有效，并通过降低切削速度来控制温度，以获取较高的表面质量。

目前，对弹性磨具的研究多针对其磨削工艺参数，集中体现为对其工艺参数的优化和获取磨抛去除模型等。而由Preston方程[5]可知：磨粒的去除深度正比于接触压力与相对速度，但由于弹性磨具的弹性变形难以确定，通过控制切削深度间接控制接触压力不如直接对接触压力进行控制有效。传统数控机床刚度较大，定位精度较好，但是价格比较昂贵，灵活性较差，在曲面打磨过程中不能紧贴工件表面，从而产生磨削加工痕迹，降低了工件表面的光洁度。对于这类曲面加工，机器人辅助磨削可替代数控机床磨削，并提高工件表面加工精度[6]。目前的工业机器人在刚度、定位精度与重复定位精度方面略有不足，使磨削加工中的接触压力不稳定，导致加工精度下降。因此，机器人磨削加工中必须控制接触压力大小，对接触压力进行反馈调节，从而能够主动适应环境的变化，满足生产加工需求[7]。

在机器人辅助磨削基础上加入力学传感系统，针对球形弹性磨具，以磨具的下压量为自变量，磨具与工件的接触压力为因变量进行有限元接触仿真，对下压量-接触压力仿真结果进行曲线拟合，并通过接触实验验证模型的准确性，以此建立基于环境模型修正的阻抗力控模型，并进行自由曲面力控实验。以实现对球形弹性磨具磨削接触压力的有效控制，并用稳定的接触压力加工复杂曲面工件。

1 基于环境模型修正的阻抗控制建模

1.1 阻抗控制系统建模

阻抗控制是一种适用于解决机械与环境交互任务的控制方法，最早由HOGAN提出[8]。阻抗控制在机械臂中的应用是分析机械臂与环境在接触状态下受的外力和机械臂的运动变量之间的函数关系，从而通过控制机械臂的运动变量，间接控制机械臂与环境之间的接触力，以提高机器人的操作性能，同时保证磨削加工中一定的安全性。

通常情况下，阻抗关系用微分方程表示为：

(1)

式中：Md、Dd和Kd分别表示机械臂辅助磨削系统的惯性、阻尼与刚度矩阵，F表示机械臂与环境间的接触压力(以下简称“压力”)，x表示机械臂末端执行器的实际位置，xr表示机械臂末端执行器的期望位置。

由于机械臂与环境间的接触压力F是随着时间不断变化的，力传感器采集的压力信号以一定的频率发送至阻抗控制系统中，因此需要对连续的阻抗系统进行时域离散化。对式(1)进行Laplace变换，可得阻抗模型的传递函数ΔX为：

(2)

ΔX=x-xr

(3)

即：ΔF=(MdS2+DdS+Kd)·ΔX

(4)

式中：ΔX表示机械臂末端执行器的实际位置与期望位置的偏差，即对位置的阻抗补偿量；S为Laplace变换后的复变量。式(4)化为时域形式得：

(5)

对时域系统进行离散化，并向后差分离散可得：

(6)

(7)

式中：T表示采用周期，ΔX(k)表示当前时刻的阻抗补偿量，ΔX(k-1)与ΔX(k-2)分别表示上一时刻与再上一时刻的阻抗补偿量。

式(6)和式(7)代入式(5)可得：

(8)

即：

(9)

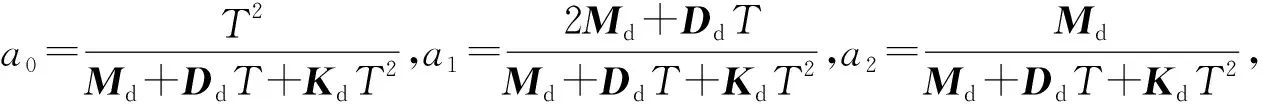
ΔX(k)=a0ΔF+a1ΔX(k-1)+a2ΔX(k-2)

(10)

由式(10)可知：当前的阻抗补偿量与接触压力、上一时刻的补偿量、再上一时刻的补偿量有关[9]，与系统响应速度和系统的惯性、阻尼与刚度矩阵有关。由于环境刚度往往是未知的，因此传统的阻抗控制是通过调节系统惯性、阻尼与刚度矩阵3个系统参数，并读取其实时接触压力来进行实时位置补偿的，补偿效果由惯性、阻尼与刚度矩阵3个参数决定。但在复杂曲面磨抛加工时，由于存在机器人的定位误差与工件的装配误差，导致磨具与工件间的接触压力不断变化，从而影响实际的阻抗补偿效果。因此，采用一种基于环境模型修正的阻抗补偿方法。

1.2 基于环境模型修正的阻抗补偿方法

基于环境模型修正的阻抗补偿方法由位置控制外环、环境模型与阻抗控制内环组成。其中：位置控制外环是由机械臂控制器控制机械臂进行笛卡儿坐标运动；环境模型将读取的接触压力换算成磨具与工件间的接触变形量，同时将阻抗控制内环输出的位移补偿量转化为接触压力的变化量；阻抗控制内环将实际接触压力与期望接触压力的差值转化为机器人的位移补偿量并输出至位置控制外环进行位置补偿。补偿算法框图如图1所示。

图1 基于环境模型修正的阻抗补偿算法框图

与传统阻抗控制相比，基于环境模型修正的阻抗补偿算法的优点在于：

(1)在阻抗响应方面不需要考虑系统的实际刚度、惯性与阻尼比，只需要让系统快速响应并达到稳定。

(2)不会受到曲面插补时实时变动的接触力的干扰，提高了系统的实时性与稳定性。

(3)能够针对不同的环境模型产生不同的控制效果，控制柔性强。

基于环境模型修正的阻抗补偿方法的核心是获得较为精确的环境模型。为了获取该模型，需要对环境刚度进行仿真与实验验证。

2 环境模型的仿真分析与实验验证

2.1 表面接触静力学仿真分析

球形弹性磨具与工件之间接触的环境模型指的是球形弹性磨具与工件接触时的接触压力与下压量之间的关系。为探究这一关系，使用ANSYS Workbench进行有限元仿真分析。磨具为聚氨酯磨头，工件材料为铝合金，聚氨酯磨头与转轴固定连接，转轴末端施加固定约束，转轴和磨具与工件接触点法向的夹角为30°[10]。每0.1 s的下压增量为0.1 mm，总下压量为0.60 mm。磨具与工件的仿真参数如表1所示，仿真模型如图2所示。

表1 磨具与工件的仿真参数

图2 球形弹性磨头有限元仿真模型

图3、图4分别为下压量为0.60 mm时的磨具与工件的有限元仿真等效应力和应变分布图。提取接触点的压力随下压量变化的数据，接触压力随下压量变化的曲线如图5所示。图5中，下压量在0～0.20 mm时，压力变化量较小；在 0.20～0.30 mm时，压力变化量逐渐增大；在0.30～0.55 mm时，下压量与压力近似呈正比关系。提取磨头变形量随下压量变化的数据，磨头的接触变形量随下压量变化的曲线如图6所示。图6中下压量在0～0.20 mm时，磨头的接触变形量较小；在0.20～0.55 mm时，下压量与磨头的接触变形量呈近似正比关系。

(a)磨头Grinding head(b)工件Workpiece图3 磨头和工件的等效应力分布图Fig. 3 Equivalent stress distribution diagrams of grinding head and workpiece

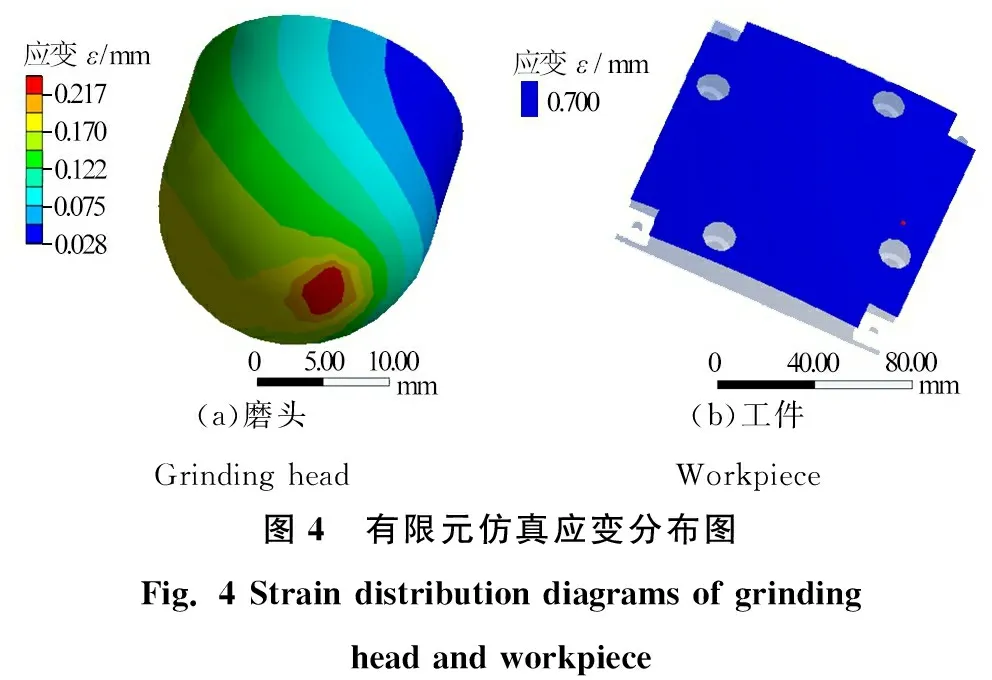
(a)磨头Grinding head(b)工件Workpiece图4 有限元仿真应变分布图Fig. 4 Strain distribution diagrams of grinding head and workpiece

图5 接触压力变化仿真曲线

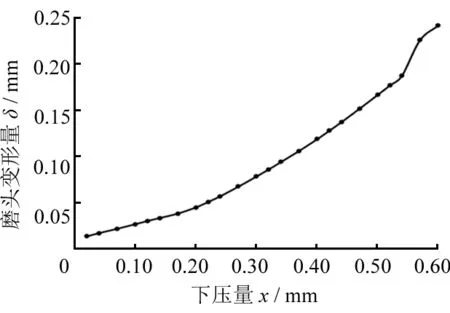
图6 接触变形量变化仿真曲线

对压力随下压量变化的数据点进行曲线拟合，结果如图7所示，拟合的高斯曲线能较完整地反映其变化趋势，且高斯曲线公式满足环境模型的计算要求。为验证模型的准确性，需要对磨具与工件进行接触实验。

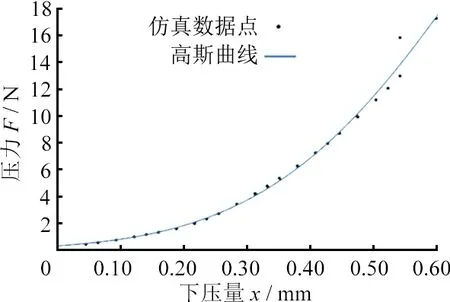
图7 高斯曲线拟合

2.2 接触实验验证

通过有限元仿真分析可得，球形弹性磨具和工件之间的接触压力与下压量的关系满足高斯分布。为了验证仿真分析的准确性，使用相同的弹性磨具进行接触实验。使用固定下压增量，分别测量磨具与工件刚接触瞬间(0 s)与接触一段时间后(2.5 s)的压力变化情况。由于弹性磨具磨削时的接触压力在10 N左右有较好的效果[11]，因此将压力设为10 N，环境模型测量范围设为0～15 N。下压量与接触压力实测对照数据如表2所示。下压量与实测接触压力对照曲线(以下简称刚度曲线)如图8所示。

表2 下压量与实测接触压力对照数据

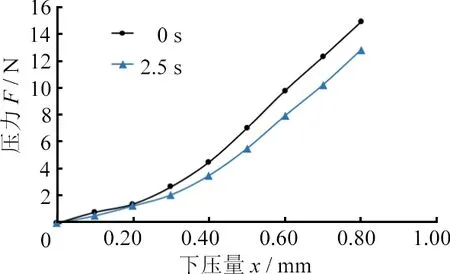
图8 下压量与实测接触压力对照曲线

图8中：在相同的下压增量下，0～0.20 mm范围的压力变化量较小；0.30～0.50 mm时，随着下压量增大，压力的变化量逐渐增大；0.50～0.80 mm时，下压量与接触压力几乎呈正比关系。对0 s时刻的实验数据进行曲线拟合，结果如图9所示，其拟合曲线符合高斯分布。

图9 高斯曲线拟合

从图9中的拟合效果来看，在F=0～15 N范围内，高斯曲线能够较好地拟合下压量与实测压力的关系。因此，可近似地将高斯模型作为球形弹性磨具与工件接触的环境模型进行阻抗控制。高斯拟合表达式为：

(11)

其中：F为接触压力，x为下压量，参数a影响高斯曲线的峰值，参数b影响高斯曲线的0点位置，参数c影响高斯曲线的对称轴位置。可以通过改变a、b、c的值对高斯曲线进行微调。

将式(11)作为球形弹性磨具与工件接触的环境模型，逆环境模型为：

(12)

阻抗控制过程可简述为：控制器控制机器人运动至新的路点，传感器测得实时接触压力，通过式(12)将传感器的实测压力Fr转化为环境的初始变形量xi，将xi代入式(11)得到接触压力Fr′；阻抗补偿小闭环将接触压力Fr′与期望力Fd的偏差值Fe转化为补偿量xe，初始变形量xi减去补偿量叠加值xe′后通过式(11)得到新的Fr′；直到偏差值Fe达到稳定，输出补偿量的叠加值xe′，在下一路点进行补偿，补偿后的点即满足力控要求。

3 球形弹性磨具的力控实验

3.1 实验条件

实验采用Epson C4-A901S六轴机械臂，机械臂末端与六维力传感器通过法兰连接，气动主轴与六维力传感器也通过法兰连接；球形弹性磨具通过筒夹加装在主轴上；工件采用直径为500 mm的球形6061铝合金曲面。实验平台如图10所示。由PC端自主研发的力控程序与机器人控制器Epson RC+共同完成控制任务，其软件界面如图11所示。实验前对工具重力、工件位置和刀具长度分别进行标定。

图10 六轴机械臂磨削实验平台

图11 小磨头力控磨抛工艺控制软件界面

3.2 实验流程与结果分析

选用球形聚氨酯基体磨具，固结磨粒为粒度代号为30/35的金刚石。首先进行机器人磨削轨迹的离线编程，编写Epson C4-A901S机器人描述文件并导入PowerMill机器人库，设定机器人磨削加工参数，且为了避免边缘效应，选择工件中心圆形区域进行磨削实验。设定磨削倾角为30°，步距为1 mm，导出编程轨迹并输入力控程序。在力控程序中，对磨具重力进行补偿后，执行力控程序。

设定期望压力值为5 N，重复多次实验，取1#、2# 2组实验结果进行分析，力控实验结果如图12所示。图12的结果表明：经过环境模型修正的阻抗补偿程序，能够使球形弹性磨具与工件间的接触压力稳定于期望力值，力控误差在±0.5 N内。其中，在t=10 s时，磨头开始接触工件，此时的初始接触压力约为1.5 N。阻抗补偿系统将实际接触压力转化为位置补偿量，并在机器人的后续路点的工件法线方向进行补偿，直到接触压力达到期望力的阈值范围内。同时，从图12中还可以看出：在补偿量较大的点位，如t=18 s时，磨头与工件间会出现一定的冲击作用，使接触压力产生较大的超调量，从而导致力控初期接触压力产生波动，这些波动在后续的补偿中逐步减小，接触压力逐步趋于稳定。这种冲击作用是由于补偿运动中磨头与工件接触时的加速度过大导致的，可以通过调节磨头与工件接触时的加速度来减小冲击；在t=30 s时，接触压力基本达到稳定。由于机器人插补时做直线运动，使其在曲面两点间运动时的接触压力产生微小波动，但这种波动对力控效果影响较小，可忽略不计。

(a) 1#

4 结论

针对球形弹性磨具磨削接触压力控制问题，建立基于环境模型修正的阻抗控制策略。对环境接触模型进行有限元仿真和实际接触实验，并对仿真实验结果进行曲线拟合，确立其环境接触模型。以此开展球形弹性磨具的力控实验，并对实验过程的接触压力进行实时测量与分析，得出以下结论：

(1)球形聚氨酯磨头与铝合金工件接触的环境模型可用高斯曲线进行描述。

(2)球形弹性磨具的力控实验结果表明，基于环境模型修正的阻抗控制策略能够得到较为稳定的曲面研磨接触压力，力控误差在±0.5 N。