基于峭度准则的轴承故障信息分析方法

徐洲常 王林军 刘晋玮 黄文超 陈保家

(1.三峡大学 水电机械设备设计与维护湖北省重点实验室,湖北 宜昌 443002;2.三峡大学 机械与动力学院,湖北 宜昌 443002)

轴承是旋转类机械设备中常见的零件之一,运行过程中极易出现故障,因此,轴承早期故障诊断方法的相关研究就十分必要.但通过分析实测的滚动轴承早期故障数据发现,这类信号中常混有较强的噪声干扰成分,具有非线性和非平稳的特点,故障诊断不易进行.针对轴承故障信号提取问题,周小龙等[1]提出了一种基于总体包络均值经验模态分解和虚假模态函数剔除算法相结合的改进HHT 方法,该方法能够准确提取故障特征.李华等[2]利用改进的变分模态(VMD)对原始故障信号进行处理,得到若干IMF 分量,根据共振频率筛选有效分量,解调分析选出的分量得到故障特征频率.李辉等[3]利用相关性分析、WPT 以及EMD 分解方法对振动信号进行处理,消除信号中的噪声成分并提取出故障特征频率.郭俊超等[4]提出了一种基于EEMD 分解、小波阈值和调制信号双谱(MSB)的多级降噪方法,能够有效提取故障特征.王林军等[5]对原始信号进行自相关去噪,去噪信号进行EMD 分解再重构,分析处理重构信号,获得轴承故障特征频率.王洪超等[6]利用EEMD 方法分解轴承振动信号得到若干IMF 分量,选择峭度值最大的分量进行改进小波变换,再通过包络解调处理提取故障特征.孟祥川等[7]通过小波阈值降噪与CEEMD 分解相结合的轴承故障分析方法处理振动信号,处理结果再进行Hilbert变换,最终得到故障特征.陈保家等[8]通过VMD 分解和改进的解调方法对轴承信号进行处理,得到有效信息从而完成滚动轴承的故障诊断.上述方法通过VMD、EMD 或EEMD等手段将信号分解为若干分量,但在区分这些分量真伪时,不能有效地筛选出包含轴承故障信号成分的分量,对于分量的信息挖掘能力存在不足.同时振动信号中常混有大量干扰和噪声,依靠小波包变换和EEMD 分解等方法的个别使用,无法得到清晰的故障特征信号[9].针对上述不足,本文提出一种利用峭度准则筛选分量,并结合多层降噪处理的轴承故障信息分析方法.该方法首先根据小波包变换原理处理原始振动信号,选择能量占比最高的频带重构振动信号,实现初步去噪.变换后的信号通过EEMD 处理得到若干个IMF分量,依据峭度准则优选分量完成轴承信号的重构.重构的轴承信号用自相关去噪方法处理,并取处理后的重构信号包络谱进行分析,获取轴承故障信息.

1 小波包变换原理

从数学角度分析,小波包变换是把信号投影到由小波包基函数构成的空间中;从信号处理角度看,它是用一系列中心频率不同但带宽相同的滤波器处理信号.给定小波函数和正交尺度函数,则有以下关系:

当n=0时,w0(t)=φ(t),w1(t)=ψ(t),得到函数集合{w n(t)}n∈Z为由w0(t)=φ(t)所确定的小波包.

设f(t)为一时间信号,p ij(t)表示第j层上的第i个小波包,称为小波包系数.G,H为小波分解滤波器,G与φj(t)有关,H与尺度函数有关.二进小波包分解的快速算法为:

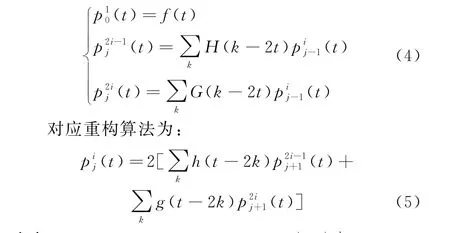
式中:j=J-1,J-2,…,1,0;i=2j,2j-1,…,2,1;J=log2N;h,g为小波重构滤波器,h与尺度函数有关,g与φj(t)有关.

本文采用小波包变换对原始振动信号进行预处理,对分解信号所得频带中能量最高的部分进行重构,降低信号复杂度,为下一步EEMD分解奠定基础.

2 基于EEMD的信息提取

经验模式分解(EMD)对信号进行时频局部化分析,即将信号分解为一系列IMF分量的和.该方法具有良好的自适应性,但它存在许多诸如模式混淆和边界效应的问题,不利于信号特征提取.为解决这些问题,相关学者对EMD 方法进行了改进,提出了集合经验模态分解(EEMD).EEMD 根据白噪声频谱分布均匀的特性,向待分解信号中加入白噪声,抑制了EMD产生的模态混叠,使分解结果更优[10-11].分解步骤如下:

步骤1):在原信号x(t)中加入高斯白噪声n(t),得到信号X(t):

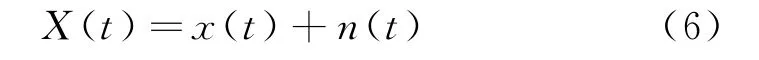
步骤2):对信号X(t)进行EMD 分解,得到n个IMF分量和余项:

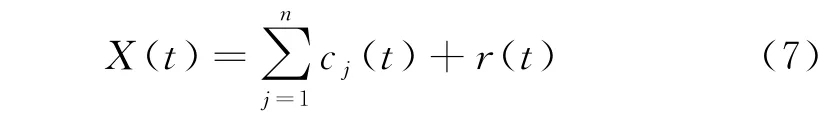
步骤3):给信号x(t)叠加不同幅值的高斯白噪声n(t),其中i=1,2,…,M,得到不同的待分解信号X(t),对这些信号X i(t)分别进行EMD 分解,得到n个模态分量(IMF)c i,j(j=1,2,…,n),其中c i,j表示含噪信号X i的第j个IMF.将得到的IMF分量进行总体平均处理,处理后的IMF即为最终结果,分量表达式为:

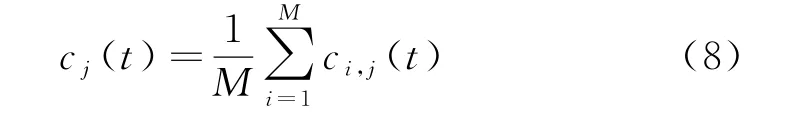
式中:c j(t)是对信号进行EEMD 处理后得到的第j个IMF,j=1,2,…,n.

3 分量的选取

信号故障特征信息的分布特性可通过峭度指标描述[12],该指标表达式为:

式中:Xms表示振动信号的均方根值;x(i)为振动信号;N为振动信号的点数.

分析公式(9)可知,峭度是一个服从正态分布的4阶无量纲参数,其值通常与机械的载荷、转速以及大小等因素无关,而冲击成分对其值影响较大,该指标常用于轴承故障分析与诊断.若有一正在运行的机械装置,测其振动信号并求解信号的峭度值K.当K=3,说明该机械运行正常;当K＞3时,则说明该机械已发生故障;当K值不断增大时,说明故障程度在不断加深.因此,在优选IMF 分量时尽量选择K值较大的分量,可充分利用分量信息.依据以上筛选准则,选出若干分量完成振动信号的重构.

4 自相关去噪原理

若有随机信号x(t),其均值m(t)大小为0,则信号的自相关函数为[13-14]:

式中:R xx(τ)、R nn(τ)分别为信号x(t)和信号n(t)的自相关函数;R xn(τ)、R nx(τ)为信号x(t)与信号n(t)间的互相关函数.当τ≠0 且取值较大时,则有R xn(τ)、R nx(τ)及R nn(τ)的值趋于0,由公式(12)可得:

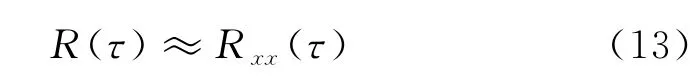
实测的轴承振动信号是一个混有噪声和干扰的周期函数,其中轴承信号与噪声信号相关性较小,轴承信号与自身相关性较大.自相关降噪正是根据这一原理实现随机噪声和干扰信号的消除,并从振动信号中分离出轴承故障信号的.

5 滚动轴承故障信息分析实例

式中:Z为滚珠个数;d为滚珠直径;D为节圆直径;α为接触角;ni为轴承内圈转速.

根据轴承的特征频率计算公式(14)～(16),可计算得到内圈故障轴承特征频率为fi=157.76 Hz,外圈故障轴承特征频为fj=104.57 Hz,轴承转频为Fr=29.95 Hz.

从时域和频域的角度分析实测的轴承内圈信号,其结果如图1所示.

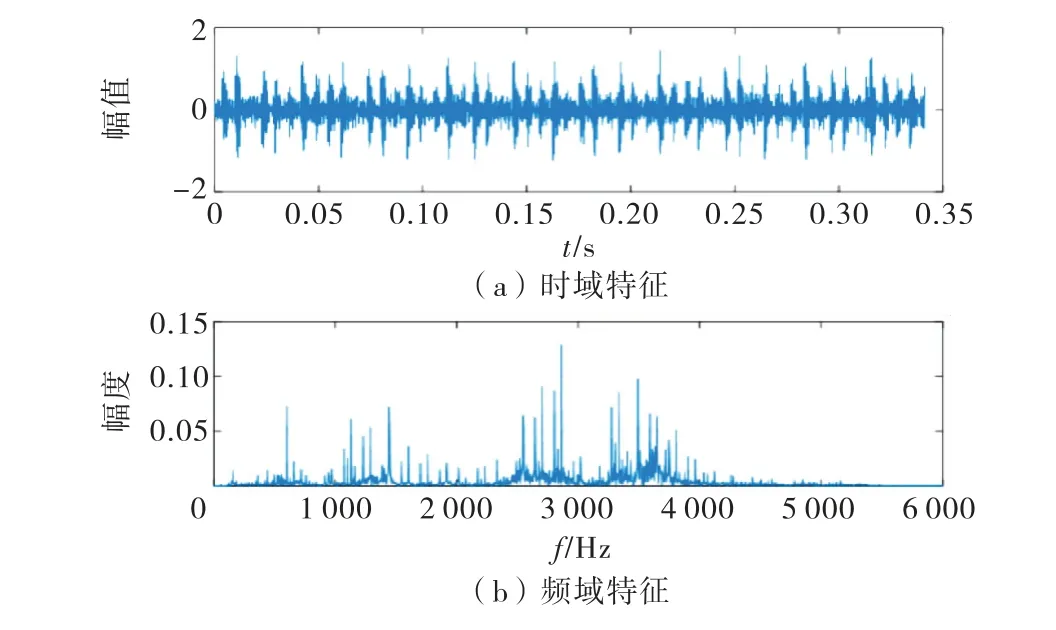
图1 内圈信号时域和频域特征

由图1可知,原始振动信号中包含大量随机噪声和干扰,依靠频域分析结果获取轴承故障信息较困难,因此,要对原始信号进行相关处理.本文用小波包变换处理振动信号,分解层数设为3,计算第3层各频带的能量分布,结果如图2所示.

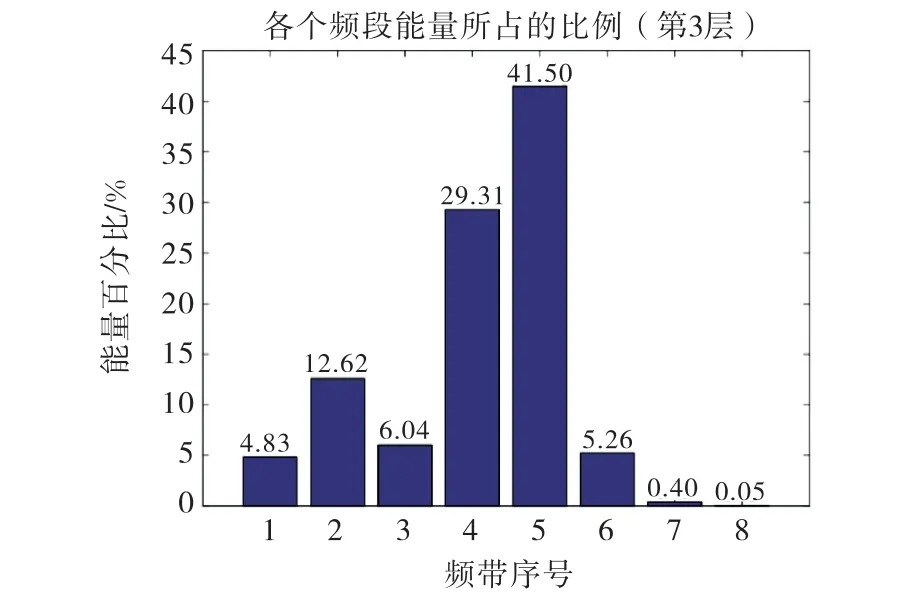
图2 内圈信号WPD 处理后的频带能量分布

分析图2,发现信号的能量主要集中在第5个节点,利用该节点重构信号,重构结果如图3所示.

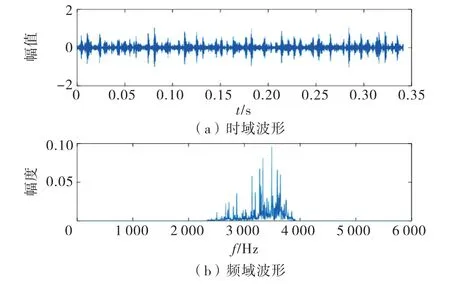
图3 WPT 处理后振动信号时域和频域波形

对比图1与图3,可看出原始振动信号通过小波包降噪处理后消除了大部分噪声信号,但故障特征信号仍不明显,仅依靠小波包变换处理无法得到清晰的故障信号,所以用EEMD 方法对小波包变换后的信号进一步处理,同时计算信号处理后所得分量的峭度值,见表1.

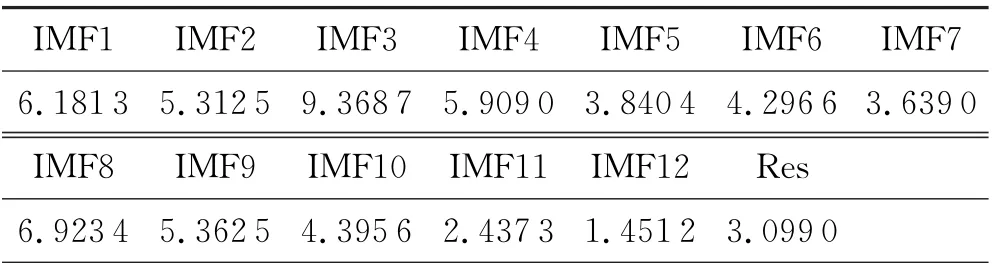
表1 分解内圈信号所得分量的峭度值

从表1中可看到,分量1～10峭度值较大,为轴承故障信号成分可能性大;分量11～13的峭度值较小,属于噪声成分可能性大.利用分解结果中峭度值大于3的前10个分量来重构轴承内圈故障信号,结果如图4所示.

图4 内圈故障重构信号的时域波形

轴承内圈故障信号应具有十分明显的周期和冲击特性,但通过分析图4的信号波形图,发现重构信号仅表现出部分冲击特征,没有明显周期特性,说明信号去噪不彻底.为得到清晰的故障特征信号,用自相关方法处理重构信号,所得结果如图5所示.

图5 内圈故障重构信号自相关处理结果

处理后的重构内圈信号的包络谱,如图6所示,可知内圈故障频率和轴承的转频.分离出的故障频率为156.7 Hz,而理论计算的故障频率为fi=157.76 Hz,两者相对误差仅有0.67%,这说明从原始信号中分离出了轴承内圈故障信息.

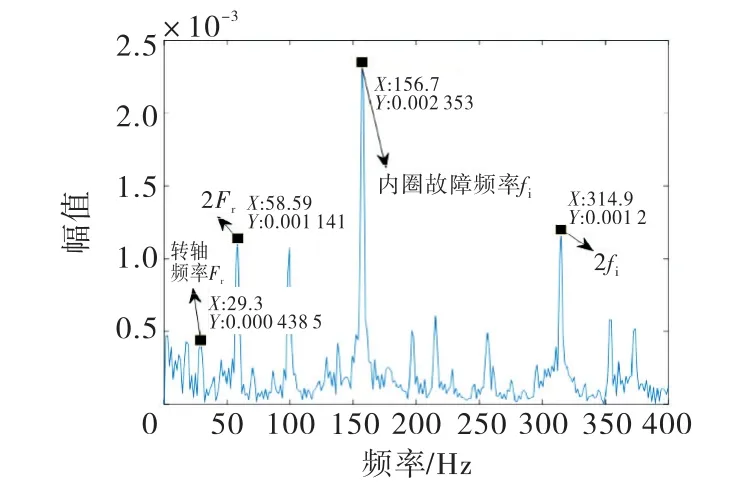
图6 内圈故障重构信号处理后的包络谱

对比图1、3、5和6的内圈故障信号处理结果,发现:利用傅里叶变换处理成分较复杂的振动信号,轴承故障频率被过多频域信息掩盖,难以分辨;利用小波包方法处理故障信号,仅能得到较为清晰的故障信号,无法获取所需故障信息;而利用本文所提方法处理轴承振动信号,不仅能得到“干净”的故障信号,还能获得故障特征频率.

用本文方法处理轴承外圈故障信号,计算处理后所得分量的峭度值,见表2.

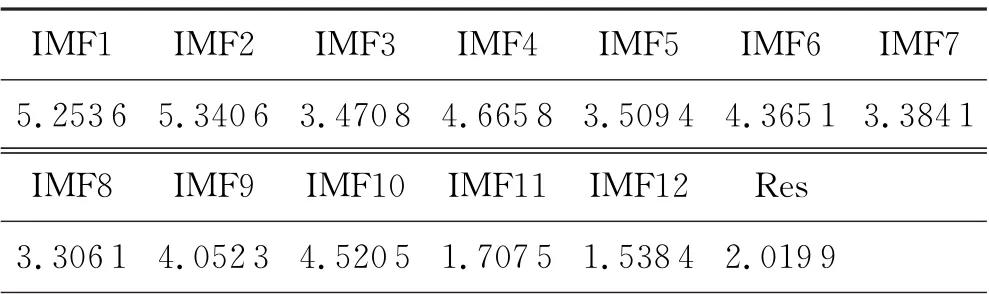
表2 分解外圈信号所得分量的峭度值

根据峭度准则,选用前10个分量来重构轴承外圈故障信号并进行自相关去噪处理,结果如图7所示.

图7 外圈故障重构信号自相关处理结果

分析图7可知,外圈故障信号同样为周期性冲击信号,且其冲击特性和周期特性都较为明显.

图8为轴承外圈故障包络谱,分析包络谱得到故障频率为105.5 Hz,而理论计算的故障频率为fj=104.57 Hz,两者相对误差仅有0.88%,这说明从原始信号中分离出了外圈故障频率.

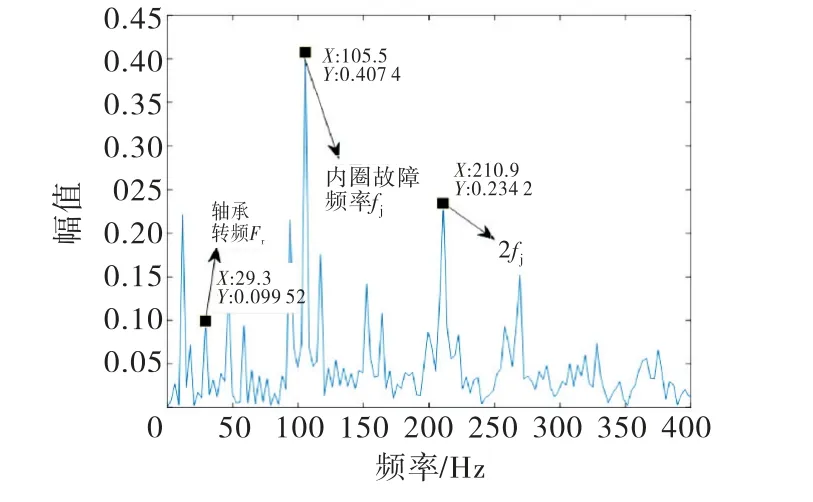
图8 外圈故障重构信号处理后的包络谱

同时比较图5和图7,可发现轴承内圈故障信号和外圈故障信号通过处理,均能突出故障信号的周期特性和冲击特性,但外圈信号处理结果更明显.

利用本文方法能得到轴承信号大致波形,根据波形判断轴承是否发生故障.使用6406型滚动轴承数据集进行验证,对6406型滚动轴承正常、内圈故障和外圈故障3组信号用本文方法处理,得到不同状态下的轴承信号的处理结果,如图9～11所示.

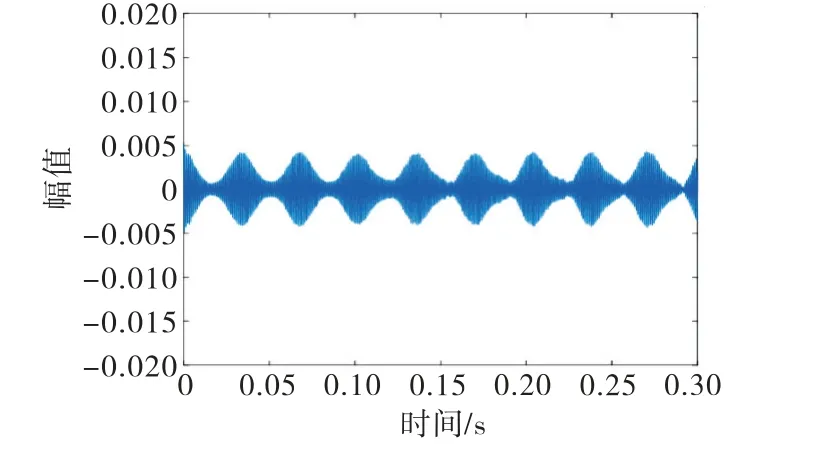
图9 6406型轴承正常信号的处理结果

6406型轴承正常信号的处理结果如图9 所示.分析图9,发现处理后的正常组信号去噪效果良好,其波动特性和周期特性十分明显.

对比图5和图10的内圈故障信号时域波形图,可看到不同型号轴承的内圈故障信号均有一定的周期和冲击特性,但周期变化不明显.

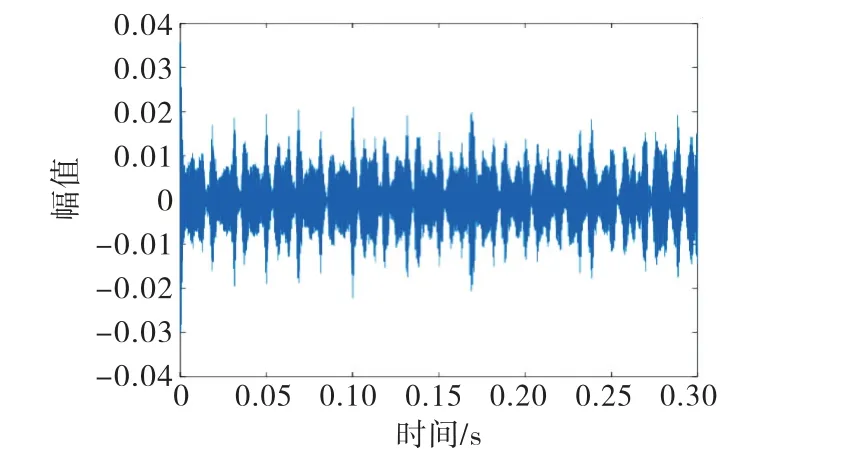
图10 6406型轴承内圈故障信号的处理结果

对比图7和图11外圈故障信号时域波形图,可发现不同型号轴承的外圈故障信号具有清晰的周期和冲击特性,且周期变化较明显.通过不同型号的轴承信号处理结果对比分析,可发现本文方法能有效去除噪声和干扰,从原始信号中分离出轴承故障特征频率,同时利用该方法处理轴承信号,可初步判断其是否发生故障.

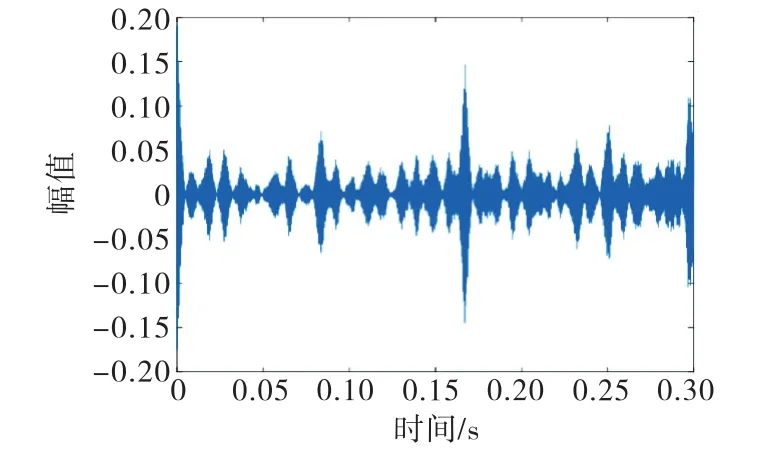
图11 6406型轴承外圈故障信号的处理结果

6 结 论

本文提出了一种利用峭度准则筛选分量,并实现多层降噪处理的轴承故障信息分析方法.通过实验结果及分析得出以下结论:

1)在滚动轴承早期出现故障时,振动信号中混有大量非周期随机干扰信号,其冲击特性表现不明显,仅使用小波包变换方法处理振动信号,并不能得到明显故障特征信号.而结合小波包变换、EEMD 分解以及自相关去噪处理的故障分析方法,可有效地增强轴承早期故障信号冲击特性,凸显微弱故障特征.

2)通过小波包变换和EEMD 分解处理振动信号可得若干IMF分量,所得分量可能含有噪声成分.可根据分量的峭度值大小区分IMF 分量的真伪,滚动轴承实测振动试验结果表明依据峭度准则能准确筛选出包含轴承故障信号成分的IMF分量.

3)通过对两组不同型号的轴承实测振动信号处理并分析,结果说明利用小波包变换、EEMD 分解以及自相关去噪相结合的轴承故障信息分析方法处理信号,能够有效消除噪声成分,并从原始信号中分离出故障特征信号,实现轴承内外圈故障的准确诊断.