基于傅里叶分解-小波包分析的爆破信号去噪方法*
2021-06-24王海龙柏皓博王海军
王海龙,柏皓博,赵 岩,王 彬,王海军
(1.河北省土木工程诊断、改造与抗灾重点实验室 河北省寒冷地区交通基础设施工程技术创新中心, 张家口 075000;2.中国矿业大学(北京) 力学与建筑工程学院,北京 100083;3.北旺建设集团有限责任公司,承德 067000)
目前,大多对于爆破的研究都是基于对爆破振动信号的研究展开的,但在进行信号采集时,受施工现场复杂环境影响,如钻孔作业、装载机与运输机等重型机运作。同时还受到信号采集仪器松动或由于温度变化产生零点漂移的影响,采样信号可能会出现形状不规则和基线偏移情况。故采集到的爆破振动信号可能带有无用干扰信号,即噪声。而噪声会对信号中有用信息的提取造成干扰,对信号处理带来困难,为进行后续爆破振动信号分析,原始信号的降噪处理就成为了不可或缺的前期工作。
由于隧道爆破的突发性,破坏性强,隧道爆破信号表现为典型的非平稳信号,处理这类非平稳信号去噪问题,较常见的方法为EMD(empirical mode decomposition)方法[1]、EEMD(ensemble empirical mode decomposition)方法[2]、CEEMDAN(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise)方法[3]、小波阈值方法[4]、小波包阈值方法[5]。同时,EMD-小波阈值方法联合去噪[6]、EEMD-小波阈值方法联合去噪[7]、CEEMDAN-小波包联合去噪在进行信号去噪中表现良好[8]。
马宏伟等利用EMD分解方法对煤矿机械振动信号进行降噪处理[9],利用相关系数,实现了非平稳信号的滤波。叶红宇等针对EMD方法模态混叠问题[10],使用EEMD-小波包阈值方法对隧道爆破振动信号进行降噪,在消除随机噪声的同时,该方法可保留更多的信号细节特征。刘霞等使用CEEMDAN方法对信号进行分解[11],利用能量熵划分噪声主区间,对其进行阈值去噪,此方法在很大程度上缓解了模态混叠问题。李红延等在小波阈值去噪算法基础上[12],改进阈值函数,提高了噪声与信号的可分离性。史贤俊等针对含噪信号的不同频段[13],采用不同小波包阈值算法,用量化后的系数重构得纯净信号。
EMD方法、EEMD方法、CEEMDAN方法均未从根本上解决噪声残留与模态混叠问题。小波阈值方法未对信号高频部分进行分析,存在局限性,而小波包阈值方法虽对高频部分进行分解,但二者均受制于小波基函数与分解层数的选取。
隧道爆破过程中,由于施工现场环境复杂,噪声对信号采集影响较大,针对此噪声干扰问题,提出一种基于傅里叶分解(FDM)和小波包阈值方法的联合去噪方法[14-17]。傅里叶分解基于傅里叶变换,进行时频分析,可以将原始信号进行自适应分解,得到一系列正交的傅里叶固有频带函数(FIBFs)和一个残余分量,可以将有用信息与噪声进行有效分离,避免了模态混叠问题的出现,可以直接将噪声分量进行剔除,保留含少量噪声与有用信息的分量,进行初步信号去噪,并且由于在分解过程中未加入高斯白噪声,也就不会存在噪声残留问题。而小波包阈值方法,优化了对信号高频部分的分析,提高了信号的分析能力。
利用FDM和小波包阈值方法联合去噪主要流程为:将原始信号分解为若干正交的傅里叶固有频带函数,通过分析相关系数,找出噪声分量,剔除噪声分量后,将剩余包含原始信号信息和少量噪声的FIBFs进行重构;利用小波包阈值方法对重构信号进一步降噪,得到降噪处理后的爆破振动信号。
1 原理阐述
1.1 FDM算法
Pushpendra Singh等学者在傅里叶变换的基础上[18],提出一种新的时频分析方法,其可用于分析非线性、非平稳信号,即FDM(Fourier Decomposition Method),此方法通过在傅里叶域内自适应搜寻解析傅里叶固有频带函数(AFIBFs),从而获得一系列傅里叶固有频带函数和一个残余分量,获得多分量信号作为常数和单分量信号的唯一表示,该数学模型可用下式表示。
(1)
式中:n(t)为残余分量;yi(t)∈C∞[a,b]为傅里叶固有频带函数(FIBFs)。FIBFs具有如下性质:函数均为零均值函数;且不同分量函数之间两两正交;FIBFs提供的解析函数的瞬时频率和瞬时幅值均不小于0。用数学表达式表示为
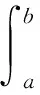
(2)

(3)
(4)
由以上性质可得,FDM方法具有完备性、正交性、局部性、自适应性,对信号进行傅里叶分解后,基本可以将信号中的有用信息与噪声分离开来,且不会发生模态混叠现象。
在搜寻AFIBFs时,可以由高频向低频搜寻(HTL-FS算法),也可以从低频向高频搜寻(LTH-FS算法),具体步骤为[19]
LTH-FS算法:

(1)对原始信号x(t)进行傅里叶变换,即X[k]=FFT{x[n]};

(4)对AFIBFs可求瞬时频率和瞬时幅值,AFIBFs的实部即为FIBFs。
HTL-FS算法:

(1)对原始信号x(t)进行傅里叶变换,即X[k]=FFT{x[n]};

(4)对AFIBFs可求瞬时频率和瞬时幅值,AFIBFs的实部即为FIBFs。
1.2 小波包算法
小波分解通过一组低通与高通滤波器将原始信号分解为高频和低频两个部分,而后将低频部分进行分解。小波包分解将小波分解中未涉及的高频部分进行进一步分解,而后再选择最优小波基函数,时频分析效果优于小波函数。其具体步骤为[20]:
(1)定义正交尺度函数φ(x)以及其对应的小波函数ψ(x),设h(k)为低通滤波器系数,g(k)为高通滤波器系数,并且有h(k)和g(k)为共轭滤波器系数。
(5)
令μ0=φ(x),μ1=ψ(x),则
(6)
(7)
可得小波包分解算法为
(8)
(3)将小波包分解进行逆运算,得到小波包重构表达式为
(9)
1.3 FDM-小波包联合降噪
基于FDM算法和小波包算法,提出基于傅里叶分解和小波包阈值方法相结合的爆破振动信号去噪方法,其具体步骤为:
(1)对原始爆破信号进行傅里叶分解,将信号分解为若干傅里叶固有频带函数和一个残余分量;
(2)根据相关系数法筛选出噪声模态分量,将剔除噪声模态分量后的信号进行重构;
(3)利用小波包阈值方法对重构信号进行降噪处理,得到纯净信号。
2 仿真分析
2.1 爆破振动模拟信号建立
利用正余弦函数叠加函数模拟隧道爆破振动信号[21],仿真信号表达式为
(10)
式中:z1(t)为原始信号;z5(t)为高斯白噪声。模拟信号建立如图1所示。
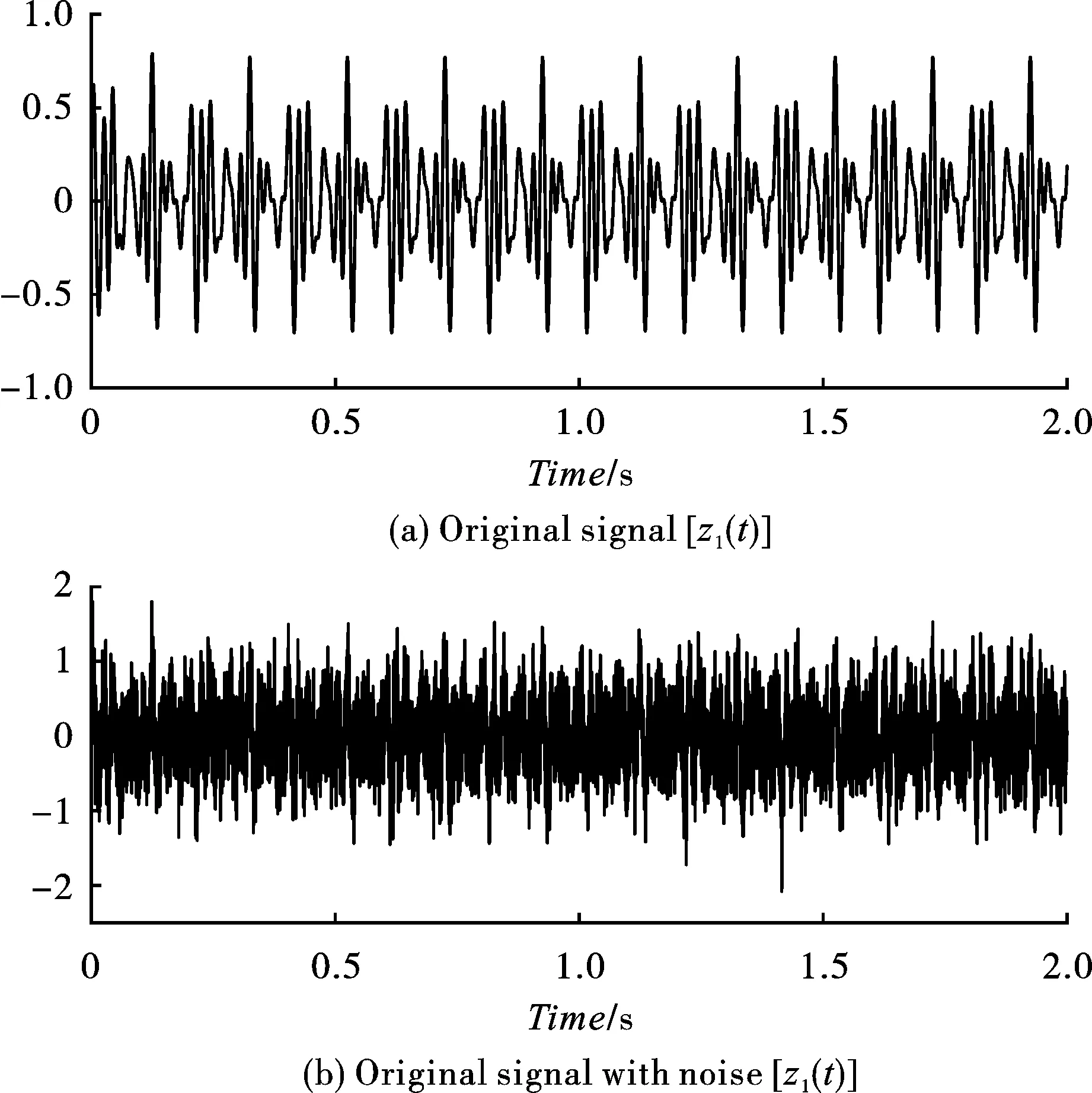
图 1 仿真信号波形图Fig. 1 Waveform of simulation signal
2.2 仿真信号的傅里叶分解及FIBFs相关性分析
对上述仿真信号进行FDM分解,采用HTL-FS算法,分解得到37个傅里叶固有频带函数和一个残余分量r,由于篇幅限制,选择其中10个模态分量进行展示如图2所示,其中y1~y3与原始信号波形相似,可初步认为其含有原始信号中有用信息,而其余分量与原始信号波形差异较大,初步认定其为噪声分量。

图 2 FDM分解结果Fig. 2 Decomposition result of FDM
对傅里叶固有频带函数与仿真信号进行相关性分析,求得傅里叶固有频带函数与原信号z(t)互相关系数,部分互相关系数如表1所示。

表1 部分FIBFs与原信号z(t)互相关系数Table 1 Correlation coefficient of part of the FIBFs and Original signal z(t)
通过互相关系数,并结合波形图可知,y4~y37相关性较小,可认为是噪声分量,将其剔除,y1、y2、y3分量与原始信号互相关系数较大,且包含原始信号细节特征,将其保留并重构,利用小波包阈值方法进一步进行降噪。
2.3 小波包阈值方法降噪
将y1、y2、y3进行重构,采用小波包阈值方法对其进行去噪处理,降噪后纯净信号如图3所示。
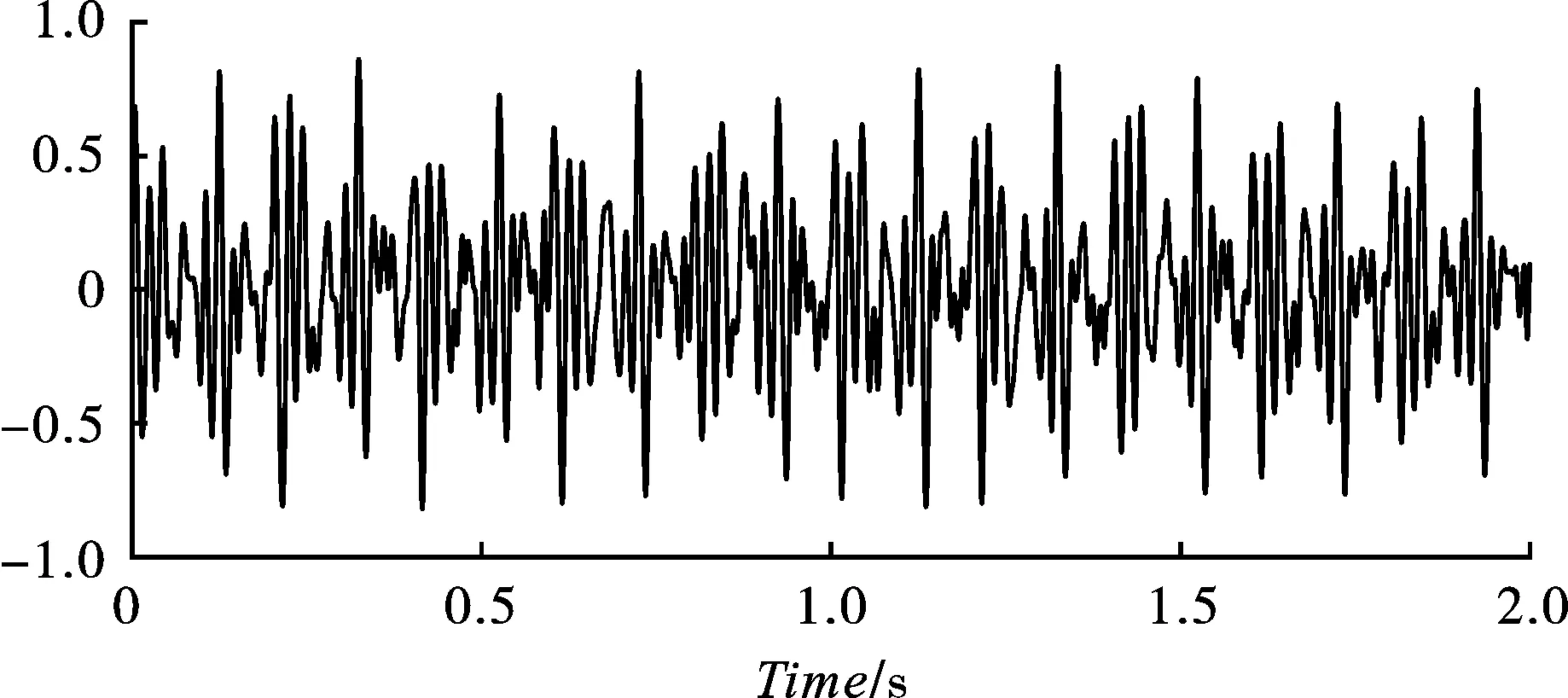
图 3 纯净信号波形图Fig. 3 Pure signal after de-noising
2.4 仿真结果评价
通过对比波形图可以发现,降噪后的纯净信号基本保留了初始信号z1(t)的特征信息,且剔除了其中的噪声信息,利用MATLAB中互相关系数函数计算纯净信号与初始信号z1(t)的相关系数为0.9575,表现出良好的相关性,可以发现,FDM-小波包联合去噪方法可以准确地去除信号中的噪声,在隧道爆破振动信号去噪中表现良好,可以得到精确的振动信号。
再通过信噪比(SNR)和均方根差(RMSE)来评价爆破信号去噪效果[22],信噪比越高,均方根差越小,说明去噪效果越好,表达式为
(11)
(12)
式中:Zi(t)为原始信号;Z′i(t)为去噪后信号;n为信号长度。
为验证此方法的降噪效果,对仿真信号分别采用小波包阈值方法、EMD-小波包联合降噪方法、CEEMDAN-小波包联合降噪方法进行分析,所得波形图如图4所示。
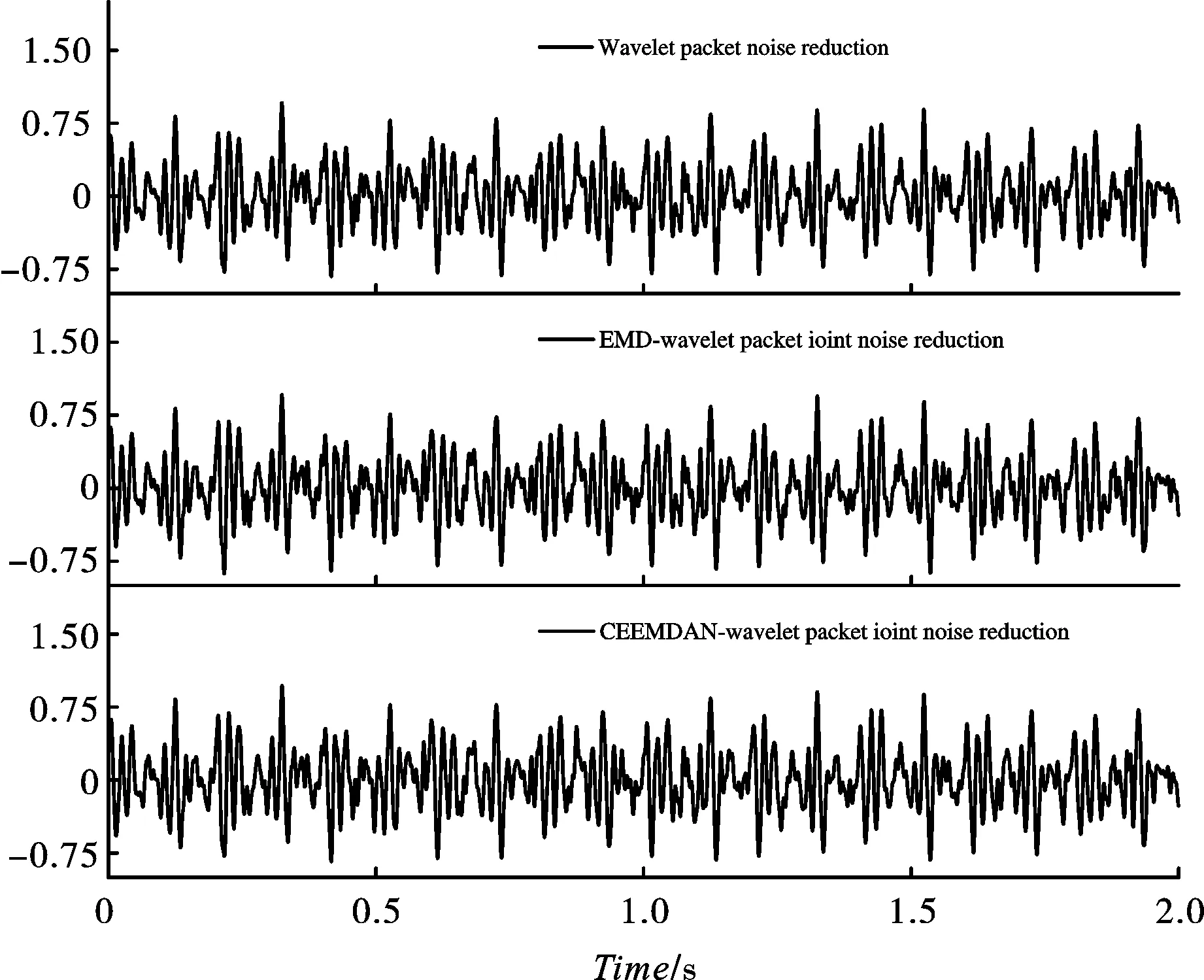
图 4 降噪效果对比图Fig. 4 Noise reduction effect of several methods for comparison
分别计算上述方法信噪比和均方根差,所得结果如表2所示。

表2 降噪效果对比Table 2 Noise reduction effect comparison
通过对比可得,FDM-小波包联合去噪方法信噪比(10.3940)最大,均方根差(0.0889)最小,去噪效果最好,同时观察波形图可知,经FDM-小波包联合去噪后,波形图的光滑程度得到显著提高,在保留原始信号细节特征的同时,有效剔除了噪声分量,证明了FDM-小波包联合去噪方法在隧道爆破振动信号去噪中的有效性。
3 工程实例分析
3.1 爆破信号采集
实测爆破振动信号来自于新建京张高铁草帽山隧道爆破施工[23,24],爆破振动信号采集仪器为中科测控公司研发的TC-4850爆破测振仪,最小工作采样频率为5Hz,原始爆破振动信号如图5所示。
由图5可知,受复杂施工环境影响,此信号爆破振速时程曲线不平滑,包含大量毛刺噪声。
3.2 FDM-小波包联合降噪
先对原始信号进行FDM分解,采用HTL-FS算法,得到48个傅里叶固有频带函数和1个残余分量r。部分傅里叶固有频带函数如图6所示,其中,y1~y5分量特征清晰,无模态混叠现象,且与原始振动信号波形相似,初步认为其包含大部分原始信号中有用信息,进行相关性分析进行验证。

图 5 爆破振动信号Fig. 5 Original signal of blasting vibration speed
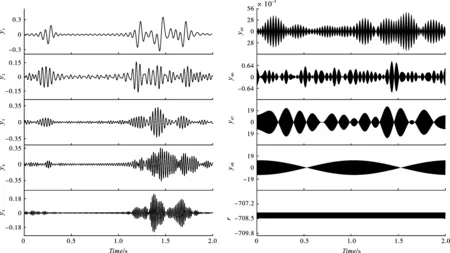
图 6 FDM分解结果Fig. 6 Decomposition result of FDM
对FIBFs进行相关性分析,部分互相关系数如表3所示。

表3 部分FIBFs与原始信号互相关系数Table 3 Correlation coefficient of part of the FIBFs and Original signal
y1~y5相关系数较大,认为其含有原始信号有用信息,其余分量相关系数较小,认为其为噪声分量,将y1~y5进行重构,进行小波包阈值方法降噪,依据采样定理[25],信号采集频率为5000 Hz,Nyquist频率为2500 Hz,故小波基函数采取“db8”函数,进行8层分解,采用软阈值进行去噪。所得纯净信号如图7所示。
3.3 去噪结果评价与分析
为评价FDM-小波包联合去噪方法,再分别采用小波包阈值方法、EMD-小波包联合降噪方法、CEEMDAN-小波包联合降噪方法对原始信号进行去噪,所得结果如图8所示。
由图8对比可知,FDM-小波包联合降噪方法所得爆破振动时程曲线相比较而言最平滑,且保留了原始信号中的细节特征,基本消除了原始信号中的毛刺噪声,去噪效果最好。而其余三种方法在进行降噪后,所得时程曲线含有毛刺噪声,降噪效果不理想。故采用FDM-小波包联合降噪方法,有助于得到更为精确的爆破振动信号,为进一步的爆破振动分析提供了更科学的基础。

图 7 纯净信号波形图Fig. 7 pure signal after de-noising
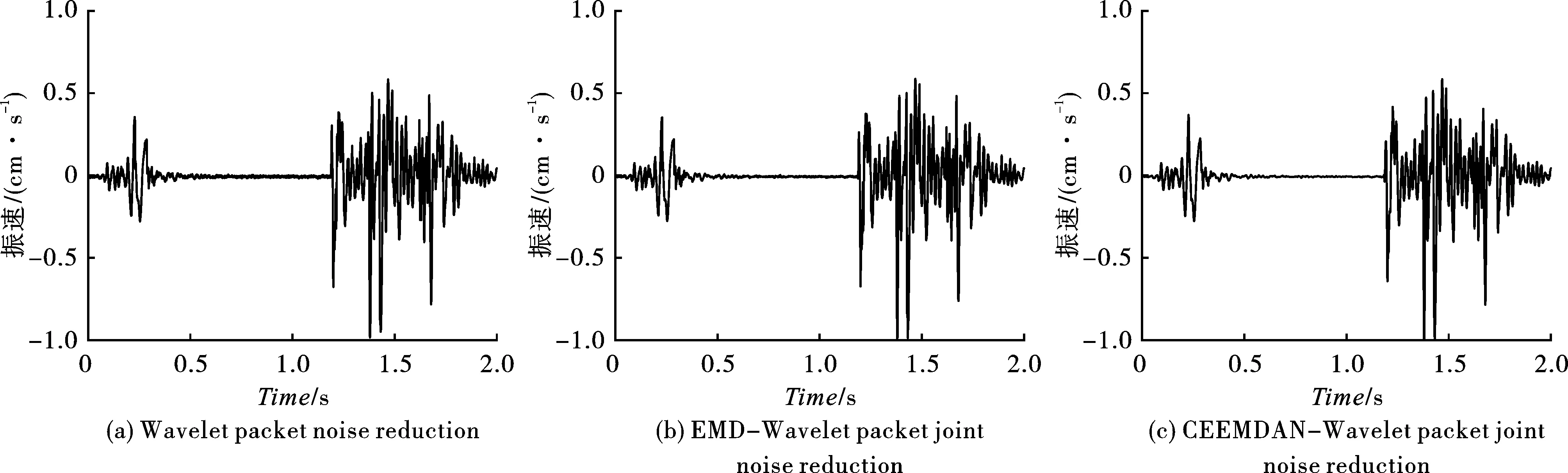
图 8 不同方法去噪结果对比Fig. 8 Noise reduction effect of several methods for comparison
对比不同方法的去噪过程,FDM-小波包联合去噪方法相对更简便,由于其可以有效将原始信号中有用信息和噪声进行分离,故只需选择相关系数较大的分量进行重构,之后利用小波包阈值方法进一步降噪,可以在最大程度上保留有用信息,消除噪声。
4 结论
依托新建京张高铁草帽山隧道爆破施工,提出了一种傅里叶分解-小波包联合降噪方法,分别对仿真信号及工程爆破振动信号进行分析,得到如下结论:
(1)FDM分解从根本上解决了模态混叠与噪声残留问题,提高了信号分解精度。
(2)与小波包阈值方法、EMD-小波包联合降噪方法、CEEMDAN-小波包联合降噪方法相比,FDM-小波包联合降噪方法所得到信噪比(10.3940)最大,均方根差(0.0889)最小,降噪效果最好。
(3)FDM-小波包联合降噪所得纯净信号可有效保留原始信号中细节特征,可为后续信号精确分析奠定基础。
