基于相场模型的裂纹贯穿程度对试件强度影响研究

高 宇 陈 颖 岳 强 王 桥 周 伟 张晨露

(1.大唐宣威水电开发有限公司, 云南 曲靖 655499;2.武汉大学 水利水电学院, 武汉 430072)

对于各个工程领域中的混凝土、岩石、砌体和陶瓷等脆性或准脆性材料,断裂破坏是它们主要的破坏形式.许多灾难性的事故都归因于结构断裂或者裂纹扩展.因此,为保证结构正常使用,对脆性材料或者准脆性材料断裂机理以及裂纹扩展等问题进行研究是十分重要的.

在理论分析方面,学者们先后提出了线弹性断裂力学[1]、内聚力模型[2]和损伤力学[3]等理论.近几十年来,计算机技术的发展为数值模拟奠定了良好的基础,许多研究学者已经提出了多种数值方法或计算力学方法对裂纹进行模拟,主要分为离散裂缝模型[4]和弥散裂缝模型[5].离散裂缝模型主要解决预知路径裂纹的问题,且裂缝只允许在单元边界扩展,需要对裂纹路径进行跟踪,过程十分繁杂;弥散裂缝模型通过对材料的应力-应变关系进行描述,可以自动模拟沿开裂方向的裂纹,无需跟踪裂纹路径,但是具有对网格排列依赖性严重的问题.针对这些弊端,又有学者在上述模型的基础上改进发展出扩展有限元法(XFEM)[6],但仍然存在边界条件难以确定,对裂缝几何描述与跟踪繁琐,人为设定因素太多等问题.

相场理论[7]是近二十余年发展起来的方法,引起了各界学者的广泛关注,并先后提出了多种相场模型[8-10].相场模型只需要对网格进行一次划分,操作简单且对网格数量不敏感,不需要对裂纹进行特别处理,能够处理复杂裂缝模式.但是现有的相场断裂模型大多只考虑了拉伸破坏,不能直接应用于剪切破坏.王桥等[11]提出了基于统一拉伸断裂准则的混合模式断裂相场模型,在模拟中可以根据材料的特性得到不同的断裂模式,包括基于最大正应力和最大剪应力准则的破坏.采用统一的拉伸断裂准则可以很容易地确定裂纹扩展方向.

大多数学者用方板来对裂纹进行数值模拟,只考虑了简单边界条件,对于初始裂缝长度只取方板边长的一半,并未探究初始裂缝长度对方板强度的影响,也未考虑初始裂纹贯穿程度在不同受力破坏状态下所产生影响的差异性.本文以有限元通用软件实现混合模式断裂相场模型,给出不同初始裂纹长度的方板在受拉伸、剪切和拉剪荷载时的算例.

1 相场断裂模型

1.1 统一相场模型

由于对各区域粒径进行了放大,需要按照尺度关系调整颗粒材料参数,以保证不同区域相应物理力学特性的一致性.

相场模型是基于Griffith断裂理论[12]的变分准则,当无体力作用时,弹性体总势能E可以表示为:

引入相场变量s∈[0,1]代表材料的损伤程度将尖锐裂纹面弥散到一定宽度的区域内.用相场s表示的裂纹面如图2所示.s=0时,代表材料完好无损;s=1时代表材料完全破坏.建立式(1)的正则化方程:

图1 弹性体中尖锐的裂纹面

图2 弥散化的裂纹面

对于传统的相场模型,一般采用α(s)=s2,然而这种形式的相场模型计算结果对参数l0有很大的敏感性,本文采用吴建营等[10]提出的统一相场模型中推导的形式,即:

1.2 控制方程

弹性体内同时得到位移场和相场,利用能量最小原理,得到公式(3)的变分形式:

其中公式(15)称为平衡方程,公式(16)称为裂纹演化方程.

将公式(4)代入式(16)中,可得到裂纹演化方程:

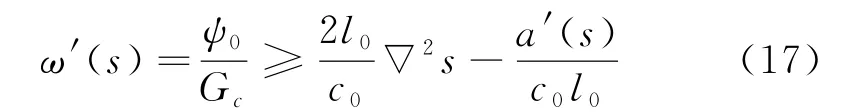
1.3 拉剪混合破坏模式的相场模型

目前的相场模型理论,绝大部分只能模拟材料的受拉破坏过程,而对其它的破坏模式无能为力,最近王桥等[11]等提出了一种适用于拉剪混合破坏模式的混合模式相场理论,通过两个不同的退化函数,将能量密度函数分解为:

式中:σt为临界拉伸破坏强度;χ为临界剪切破坏强度与临界拉伸强度的比值.

1.4 历史场

本文采用提出的分步解耦算法求解,为了防止裂纹的愈合,建立历史场变量ћ=ћI+ћII,对于初始荷载步

从而通过控制方程,即式(15)和式(31)的循环求解,即可得到最终的裂纹扩展路径.

2 数值算例

为了探究不同的初始裂纹在相同加载状态下对试件最终破坏模式的影响,对数值模拟中常用的单边缺口方板进行敏感性分析,板的边长为1.0 mm,缺口由板的左侧边界向板内延伸,其长度为d0.板的下端固定,同时对上边界施加匀速增加的位移荷载.

2.1 拉伸加载

为了探究在不同初始裂纹长度情况下,I型断裂裂纹的特征,在边长为1 mm 方板上边界施加竖直向上的位移,加载速率为每个荷载步Δu y=1.0×10-5mm,如图3所示.

图3 拉伸加载条件下方板的几何模型和加载示意图(单位:mm)

将缺口长度d0分别取0.10,0.30,0.35,0.40,0.50,0.60,0.65,0.70和0.90 mm 这9种情况.各情况下的裂纹开展路径如图4所示,对于不同的初始裂纹状态,最终的拉断裂纹路径基本一致,方板的最终破坏状态未受初始裂纹长度的影响;方板上边界的反力-位移曲线如图5所示,可见随着初始裂纹长度的增加,方板抵抗拉力的能力逐渐减弱,最大反力逐渐减小.各情况下的上边界反力峰值与对应位移见表1.当初始裂纹长度在0.3～0.7 mm 之间时,其最大反力对应的位移值几乎相同,而在这个区间之外时,随着初始裂纹长度的增加,最大反力所对应的位移值迅速减小.

图4 拉伸加载条件下的方板裂纹路径

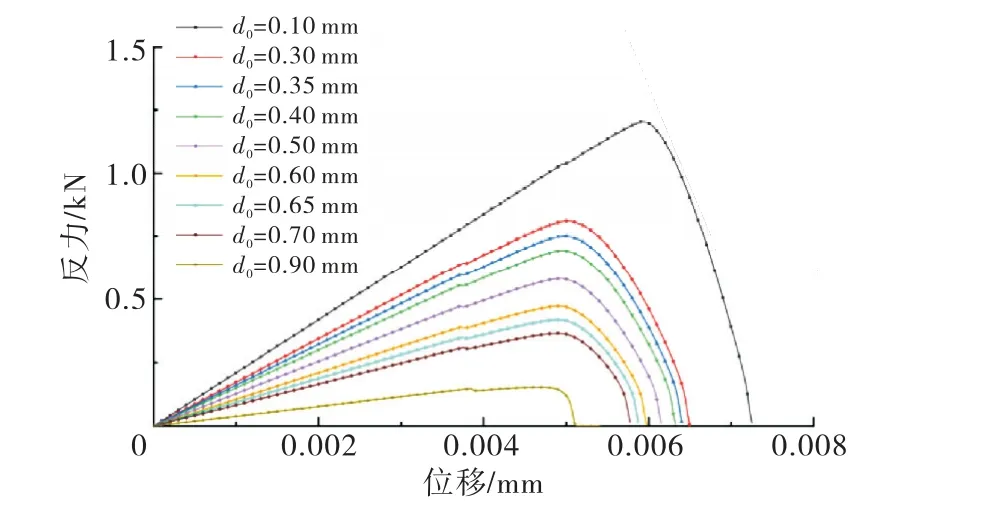
图5 拉伸加载时不同长度初始裂缝方板反力-位移曲线

表1 不同初始裂纹方板在拉伸荷载作用下反力-位移曲线峰值

2.2 纯剪切加载

此节分析不同初始裂纹长度对II型断裂的影响,为了统一性和方便性,采用和2.1节同几何条件的方板试样,初始裂纹长度的选取也同2.1节.这里对方板的底边固定,而在上边界采用水平向右的位移荷载,加载速率为Δu x=1.0×10-5mm,如图6 所示.

图6 剪切加载条件下方板的几何模型和加载示意图(单位:mm)

图7是纯剪切加载下9个不同初始裂纹长度试样的裂纹发展情况.当d0≤0.1 mm 时,方板的裂纹扩展与无裂纹扩展形式类似,即从下端剪断,此时初始裂纹对方板在受剪状态下的强度几乎没有影响.当d0≥0.3 mm 时,方板裂纹沿初始裂纹扩展且随着d0的增加,裂纹扩展的方向逐渐向下倾斜.当d0=0.3 mm 时,裂纹贯穿至方板右侧,当0.35 mm≤d0≤0.7 mm 时,裂纹沿着初始裂纹斜向下迅速扩展至方板下端直至贯穿;当d0=0.9 mm 时,裂纹沿初始裂纹贯穿至方板右侧.试样的反力-位移曲线如图8所示.

图7 剪切加载时不同长度初始裂缝方板裂纹演化情况

图8 剪切加载时不同长度初始裂缝方板反力-位移曲线

当初始裂纹长度在0.1～0.3 mm 内时,最大反力随d0减小而减小;当d0=0.35 mm 时,反力-位移曲线发生突然变化,相较d0=0.30 mm 最大反力增加0.3 k N;当d0≥0.35 mm 时,最大反力随初始裂纹长度的增加而减小,且最大反力对应的位移也逐渐减小.在剪力作用下,方板在破坏的过程中,其反力可能有多个峰值.

表2 不同初始裂纹方板在剪切荷载作用下反力-位移曲线峰值

2.3 拉剪混合加载

为了进一步研究初始裂纹对方板破坏方式的影响,这里采用拉力和剪力共同作用的方式,如图9所示,在方板的上边界同时采用竖直向上和水平向右的位移荷载,加载速率为Δu x=1.0×10-5mm 且Δu y=1.0×10-5mm.

图9 拉剪混合加载下裂缝算例的几何模型和加载示意图

图10是在拉力和剪力共同作用下9个不同初始裂纹长度试样的裂纹的发展情况.当d0≤0.5 mm时,裂纹的破坏路径是不稳定的,方板的顶部和中部均有可能发生断裂;当d0＞0.5 mm 时,方板的破坏方式逐渐稳定,裂纹由初始裂纹继续向斜下方发展直至破坏;试样的反力-位移曲线如图11所示.各个初始裂纹长度对应的反力-位移曲线峰值见表3.最大反力随初始裂纹长度的增加而减小,且最大反力对应的位移也逐渐减小.

图10 拉伸和剪切共同加载时不同长度初始裂缝方板裂纹演化情况

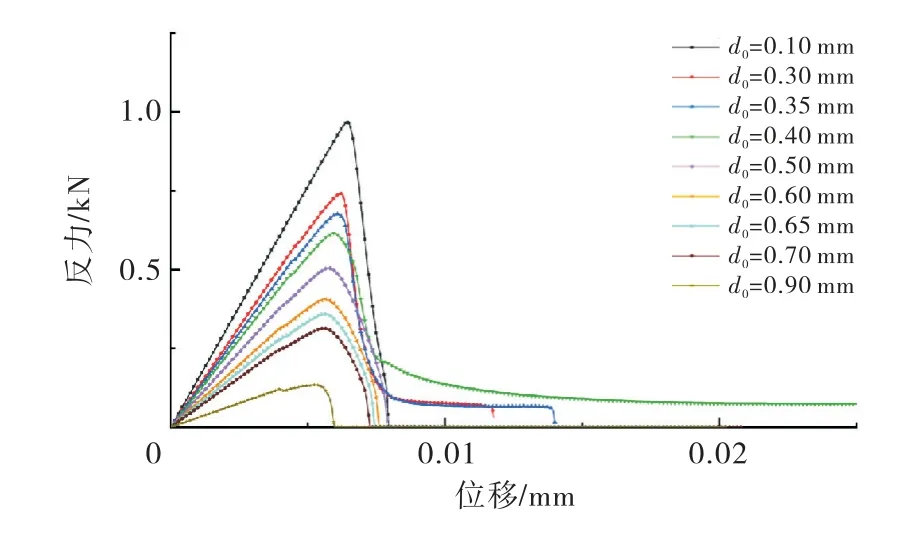
图11 拉伸和剪切共同加载时不同长度初始裂缝方板反力-位移曲线

表3 不同初始裂纹方板在拉伸和剪切荷载作用下反力-位移曲线峰值

3 结 论

本文基于适用于拉剪混合断裂模式的相场模型进行了算例数值模拟分析,探讨了断裂力学算法分析中常用的方板在不同的外力状态下和不同初始裂纹长度下的裂纹扩展路径及力学响应,主要结论如下:

1)通过算例说明了混合模式的相场模型的正确性与可靠性,能够处理拉剪混合破坏模式的裂纹模拟问题.

2)在受拉状态下,无论初始裂纹的长度多少,它的存在都会直接决定最终的裂纹路径,且破坏路径基本一致.

3)在受剪状态下,当初始裂纹长度较短时,其对方板的最终破坏模式影响较小,随着其长度的增加,方板的破坏模式逐渐由自身强度决定转变为由初始裂纹决定.

4)在拉剪混合外力作用下,随着初始裂纹长度的增加,裂纹的扩展形态逐渐由不稳定转变为稳定状态,并且由初始裂纹决定.

5)随着初始裂纹长度的增加,方板的强度逐渐减小,但在不同外力状态下,方板强度减小的规律有所区别.