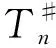Moore-Penrose逆、群逆的稳定扰动和表示

周娟娟, 朱兰萍, 黄强联

(扬州大学数学科学学院, 江苏 扬州 225002)

一些重要的广义逆, 如Moore-Penrose逆[1-2]、群逆[3-4]以及核逆[5]等的扰动分析在计算、控制理论、最优化和非线性分析等诸多领域有着广泛的应用．Nashed等首先研究了广义逆的扰动[1]和广义逆扰动的稳定条件[6]; Ding[7]给出了Moore-Penrose逆具有最简表示的充要条件; Huang等[5]讨论了核逆具有最简表示的充要条件．本文拟利用正则分解研究Banach空间中有界线性算子的Moore-Penrose逆和群逆的稳定扰动问题, 给出稳定扰动下Moore-Penrose逆和群逆的表示, 探讨扰动后算子Moore-Penrose逆和群逆具有最简表达式的充分必要条件以及稳定扰动与连续扰动的等价性．

1 预备知识

设X,Y为Banach空间,B(X,Y)表示所有从X到Y中有界线性算子组成的Banach空间, 记为B(X)．对算子T∈B(X,Y),R(T)和N(T)分别表示T的值域和核空间,I表示恒等算子, ⨁表示拓扑直和．

若算子S∈B(Y,X)满足TST=T及STS=S, 则称S为T的广义逆, 记为T+．若T+为T的广义逆, 则TT+和T+T均为幂等算子且满足R(TT+)=R(T),N(TT+)=N(T+),R(T+T)=R(T+),N(T+T)=N(T),X=N(T)⨁R(T+),Y=N(T+)⨁R(T)．反之, 若X和Y分别存在拓扑直和分解:X=N(T)⨁M,Y=R(T)⨁N, 则T存在广义逆T+∈B(Y,X)且N(T+)=N,R(T+)=M．

定义1设X,Y为Banach空间,T∈B(X,Y)．

1) 若T为单射, 即N(T)={0}, 且Y存在闭子空间N使得Y=R(T)⨁N, 则称T为浸入;

2) 若T为满射, 即R(T)=Y, 且X存在闭子空间M使得X=N(T)⨁M, 则称T为浸没．

若存在Banach空间P, 浸没S:X→P和浸入J:P→Y使得T=JS, 则称T存在正则分解T=JS．算子正则分解是矩阵论中满秩分解的推广, 并与广义逆是一一对应的．

引理2[5]设X,Y为Banach空间,T∈B(X,Y)．

1) 若T存在正则分解T=JS, 则T存在广义逆T+=S+J+:Y→X, 且J+J=SS+=IP, 其中J+为浸没且为J的左逆,S+为浸入且为S的右逆．

2) 若T存在广义逆T+∈B(Y,X), 则T存在正则分解T=JS．

定义3设X,Y为Hilbert空间,T∈B(X,Y)．若S∈B(Y,X)满足下列方程:

(1)TST=T; (2)STS=S; (3) (TS)*=TS; (4) (ST)*=ST,

其中T*表示T的共轭算子, 则称S为T的Moore-Penrose逆, 一般记为T†．

定义4设X为Hilbert空间,T∈B(X)．若S∈B(X)满足方程:

(1)TST=T; (2)STS=S; (5)TS=ST,

则称S为T的群逆, 记为T#．

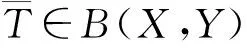
稳定扰动是保秩扰动的推广, 并且广泛应用于广义逆的扰动理论[8-11]．下面给出广义逆稳定扰动定理, 它在证明本文主要定理时起着至关重要的作用．

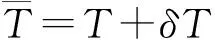
2 主要结果

下面运用正则分解给出算子在稳定扰动下Moore-Penrose逆和群逆的表达式．首先考虑算子在稳定扰动下Moore-Penrose逆的表达式．

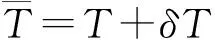
下面讨论扰动后算子的Moore-Penrose逆具有最简表达式的情形．

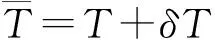
注9推论8改进了文献[7]中定理3.1的证明, 此处用正则分解的方法简化了证明．

下述定理说明对于Moore-Penrose逆, 稳定扰动与连续扰动是等价的．

定理10设X,Y为Hilbert空间,T∈B(X,Y)存在Moore-Penrose逆T†∈B(Y,X)．若Tn∈B(X,Y)且Tn→T, 则下列命题等价:

1) 当n充分大时,Tn为T的稳定扰动;

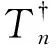
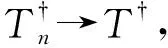
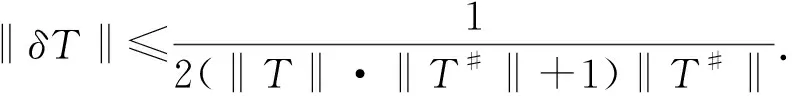
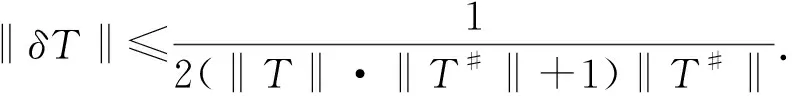
类似于定理10中(2)⟹(1)的证明,可得到下列定理．

定理13设X为Banach空间,T#∈B(X)为T∈B(X)的群逆．若Tn∈B(X)满足Tn→T, 则下列命题等价:

1) 当n充分大时,Tn为T的稳定扰动;