基于边界约束事件触发控制的异构混沌系统同步
2022-01-15林豪杰楼旭阳
林豪杰, 楼旭阳
(江南大学物联网工程学院, 江苏 无锡 214122)
混沌系统因具有初值极端敏感等特点而被广泛用于保密通信和信号处理等领域. 近年来, 多种基于Lyapunov稳定性理论的混沌系统同步控制方法相继被提出, 如驱动-响应同步[1]、耦合同步[2]、投影同步[3]、反步控制[4]和自适应同步[5]等. 由于事件触发控制策略可以减少不必要的信息传输, 故许多学者将事件触发控制与上述混沌系统同步控制方法相结合. Liu等[6]通过设计基于事件触发机制的控制器实现含传输时滞Lurie系统的混沌同步; 马大中等[7]采用基于事件触发的控制器实现异构混沌系统的主从同步. 事件触发控制下的闭环系统通常同时包含离散动态和连续动态, 是一类典型的混杂系统, 故可在事件触发下构建混杂系统, 随后在混杂系统框架下实现混沌系统同步. Postoyan等[8]通过研究非线性系统的时间触发镇定问题, 提出几种结合混杂系统的事件触发策略, 有助于进一步分析系统的稳定性和鲁棒性; Fei等[9]探讨了主从混沌系统延迟神经网络的指数同步问题, 基于延迟神经网络采用混杂事件触发控制策略设计混杂事件触发控制器, 实现了主从系统间的同步. 然而, 上述文献中的事件触发条件均被定义为状态向量或输入向量的偏差阈值, 且设置触发阈值参数为定常数, 这在实际运用中不够灵活且定常数的阈值参数选取不当会导致频繁的触发和芝诺现象. 于是, Meslem等[10]将事件触发控制下的系统建模为混杂系统, 通过分析混沌系统的稳定性和鲁棒性设计了一种基于边界约束的事件触发策略,其控制输入的更新取决于辅助系统的状态,从而避免了芝诺现象. 受文献[10]启发, 本文拟提出一种基于边界约束事件触发控制的异构混沌系统同步方法. 针对混沌系统的耦合系统,在边界约束事件触发控制下构建混杂系统, 利用驱动系统和响应间的误差系统与所设计辅助系统之间的关系对系统的控制器参数进行更新以调整误差系统的收敛率, 即通过检测误差系统的Lyapunov函数变化是否到达快慢系统的Lyapunov函数所形成的区域边界来更新控制输入, 进而利用快慢系统的收敛速度控制同步误差收敛速度以提高控制效率.
1 相关知识
考虑混杂系统
(1)
式中x∈Rn为系统状态,x可能既包含连续变量又包含离散变量, 后者通常表示为整数形式的逻辑变量; 流集C和跃集D分别表示连续动态和离散动态时的状态集合; 单值映射f: C→Rn为描述状态属于流集C⊂Rn时连续动态的函数, 亦称为流态; 集值映射G: D→→Rn为描述状态属于跃集D⊂Rn时离散动态的函数, 亦称为跃态;x+为状态跳跃后的值.
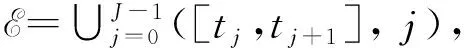
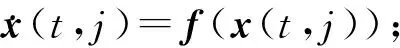
2) 对于所有的(t,j)∈domx使得(t,j+1)∈domx,x(t,j)∈D时, 有x(t,j+1)∈G(x(t,j)).如果domx是无界的, 则解x是完备的, 于是称混杂弧x是混杂系统H的解.
在状态空间Rn上的混杂系统H, 令A为状态空间Rt中的一个紧集.若对任一ε1>0, 存在δ>0使得混杂系统H从x(0,0)∈(A+δB)∩(C∪D)出发的每一个解都是完备的且满足|x(t,j)|A≤ε1, ∀(t,j)∈domx, 则称紧集A是稳定的; 如果存在正数μ>0使得系统H从x(0,0)∈(A+μB)∩(C∪D)出发的每一个最大解都是完备的且满足limt+j→∞|x(t,j)|A=0, 则称紧集A是吸引的; 如果紧集A是稳定且吸引的, 则称紧集A是渐近稳定的.令BA为A的吸引域点集, 从该点集中任一点出发的所有最大解都是完备的且收敛到A.如果紧集A在吸引域BA=C∪D上渐近稳定, 则称紧集A是大范围渐近稳定的.
引理1[12]设混杂系统H=(C,f,D,G)且A⊂Rn是闭集.若V为H的Lyapunov函数, 且存在α1,α2∈K∞和一个连续函数ρ∈P, 使得
1) 对于任意x∈C∪D∪G(D), 有
α1(|x|A)≤V(x)≤α2(|x|A);
(2)
2) 对于任意x∈C,有
〈V(x),f〉≤-ρ(|x|A);
(3)
3) 对于任意x∈D,g∈G(x), 有
V(g)-V(x)≤-ρ(|x|A),
(4)
则A对H是大范围渐近稳定的.
2 问题描述
考虑驱动系统与响应系统维数不同的异构混沌系统,其驱动系统动力学模型为
(5)
其中x∈Rn和z∈Rm为驱动系统的状态向量,f1(x,z):Rn+m→Rn和f2(x,z):Rn+m→Rm均为已知的非线性函数.响应系统动力学模型为
(6)
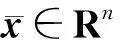
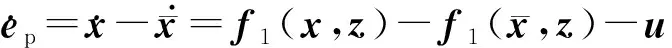
(7)
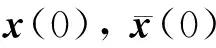
为了设计基于事件触发的控制器,假设误差系统(7)是可镇定的且存在连续控制器
u=kc(ep,z),
使得误差系统(7)在连续控制器u作用下形成的闭环系统是大范围渐近稳定的.
3 主要结果
基于连续控制器u=kc(ep,z)的形式, 针对误差系统(7)分别构造快系统和慢系统:
(8)
其中参数βf>1,βs∈(0,1), 二者分别影响快慢系统Lyapunov函数的收敛速度, 即影响事件触发的边界约束条件;ef∈Rn,es∈Rn分别为快慢系统的状态向量.
考虑事件触发控制器u=k(ep,z), 满足如下形式:
(9)
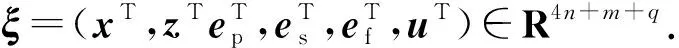
(10)
离散动力学为
(11)
其中kf,ks分别为定义离散动态ef和es的两个集值映射.
假设1假设存在一个包含原点的开集O⊂R3n, 一个连续函数kc:domkc→Rq, 一个连续可微函数Vp: domVp→R, 两个函数α1,α2∈K∞和一个函数ρξ∈P, 则
1) 对于任意ep∈domkc, 有
α1(|ep|)≤Vp(ep)≤α2(|ep|);
(12)
2) domVp=Rn且domVp×domVp×domVp包含O的一个邻域;
3) 对于任意(ep,ef,es)∈O,有
(ep,ep,ep)∈O,kc(ep,z)∈domkc;
(13)
4) 对于所有的(ep,ef,es)∈O,Vp(ef)≤Vp(ep)≤Vp(es), 有
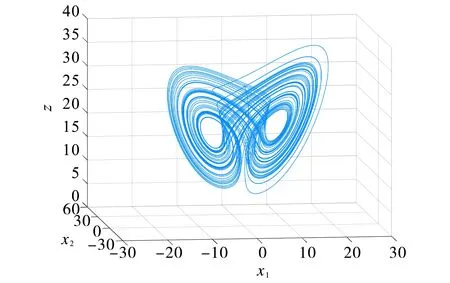
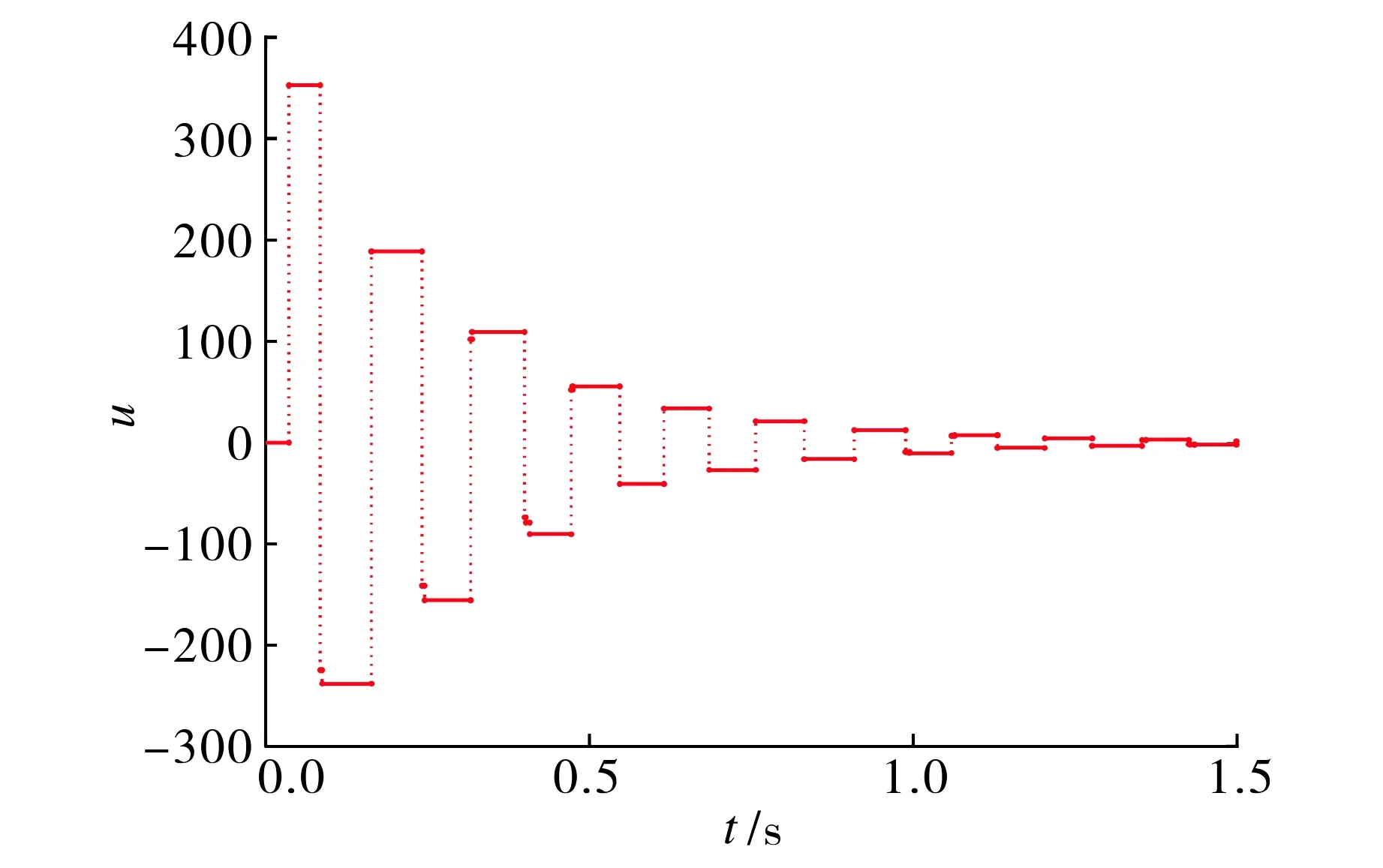
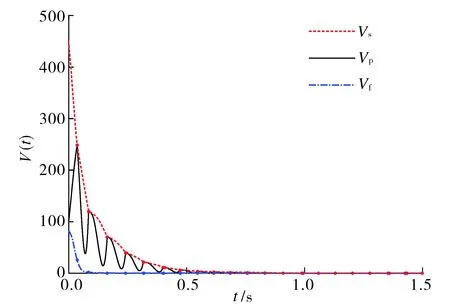
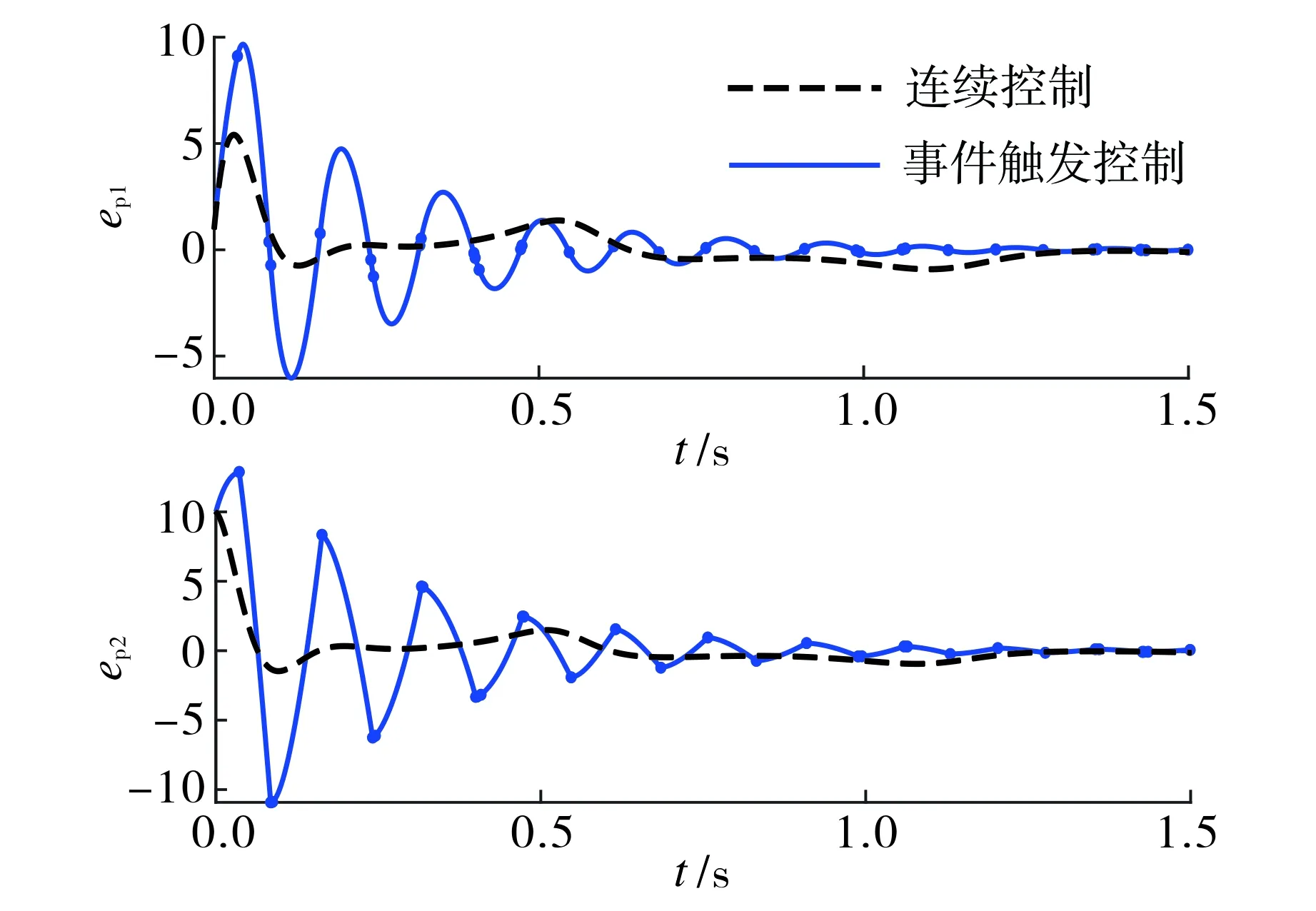
LfpVp(ep) (14) 图1 基于边界约束的事件触发控制示意图Fig.1 Block diagram of event-triggered control based on boundary constraint 对于混杂系统(10)(11),下面给出定理使得系统状态渐近收敛于集合A=Rn×Rm×{0}×{0}×{0}×Rq, 即误差信号(ep,ef,es)渐近收敛至原点. 定理1若假设1成立, 混杂系统(10)(11)的流集和跃集设计如下: (15) 则系统(10)(11)关于集合A=Rn×Rm×{0}×{0}×{0}×Rq是大范围渐近稳定的,其快慢系统的离散映射kf和ks在ξ∈Df时分别设计为 kf(ef,ep)={ep},ks(es,ep)={es}; (16) 在ξ∈Ds时设计为 kf(ef,ep)={ef},ks(es,ep)={ep}; (17) 在ξ∈Df∩Ds时设计为 kf(ef,ep)={ep}∪{ef},ks(es,ep)={ep}∪{es}. (18) (19) 其中I表示恒等映射.考虑|es|≤|ξ|A并结合式(12), 对于所有ξ∈C,有 (20) 定义映射 (21) (22) 为了便于表示, 现以f表示连续动态(10)右边部分的映射, 即 由式(13)(18),ρξ∈P以及V的定义可知, 对任意ξ∈C, 有 (23) 同时,由V和G的表达式可知, 对所有ξ∈D, 有V(G(ξ))=V(ξ).结合文献[12]定理3.18的稳定性证明可知, 闭集A对于混杂系统H是稳定的. 综上,根据文献[13]定理4.3, 系统H的任意紧致解都趋近于A, 而每个完备解都是有界和紧致的; 因此, H的每个完备解都趋近于A, 且A是吸引的.证毕. 注1文献[6,14]基于同步误差信号和采样数据分别设计了事件触发控制策略, 研究了混沌系统的主从同步问题, 但上述方法并不适用于异构混沌系统.故本文考虑的模型具有一般性, 适用范围更广泛. 注2同样是基于Lyapunov函数设计的事件触发控制策略, 本文提出的控制策略不同于文献[15]. 文献[15]中要求Lyapunov函数的时间导数在任意时刻都已知, 而本文定理1通过比较Vp和快慢系统Lyapunov函数的值放宽了此条件. 由于一个严格Lyapunov函数的计算仍很困难, 所以文献[15]是基于弱Lyapunov函数的计算, 但本文通过应用文献[12]定理3.18使得证明方法更为简单. 此外, 与文献[7,15]基于状态误差的事件触发控制策略相比, 本文所提出的触发事件设置更灵活,触发频率和控制性能可以通过辅助系统的参数进行调整,并且由于所提出的事件触发控制器和被控系统是在混杂系统框架下建立的闭环系统模型,故便于研究和分析同时具有内部状态扰动和外部干扰下系统渐近稳定的鲁棒性. 注3文献[16-17]中异构混沌系统的广义混沌同步采用连续时间触发的方式进行信息交互,导致不必要的数据信息传输, 增加了网络通信带宽. 然而, 本文基于边界约束的事件触发控制策略可以降低传输频率,减少信息的传输量和器件的损耗. 定理1虽然只考虑了异构混沌系统的完全同步问题, 但基于边界约束思想的事件触发控制方法可以推广到其他同步类型的研究中, 如文献[14-15]中的广义同步等. 为了避免在数字信号实现时系统产生无限多次的事件和控制更新,下面给出定理以使得定理1中事件触发控制下最小事件间隔时间(或两次跳跃时间间隔)大于零,即不存在芝诺现象. 定理2若假设1成立, 对于任意常数r,R,0 r≤|ξ(t,j)|A≤R,∀(t1,j1) ≤(t,j) ≤(t2,j2), (24) 其中t2-t1≥tmin. (25) 由此可见, 集合Csub与定理1中跃集D之间的距离是正的.由于系统H的流动力学是由一个连续的映射所定义, 且集合N是紧致的, 所以在N中演化的解具有一个有限最大速度M.于是, 在N内从Csub到D的演化需要一段时间, 该时间tmin由Csub和D之间的距离决定.任何在N中演化的解在离散跳跃一次后连续动态演化时间tmin>0.该离散跳跃之间的最小时间间隔tmin对于所有在N中演化的解都是一致的, 即对于H中所有满足式(24)的解是成立的. 证毕. 注4本文证明了所提事件触发控制方法不存在芝诺现象, 具有现实意义. 若仅设计与慢系统Lyapunov函数相关的事件触发采样算法也可以确保系统的稳定性, 但为了保证系统收敛速度在期望区间内, 本文设计的辅助系统包含快系统和慢系统. 为了验证本文方法的有效性,考虑如下Lü系统[18]: (26) 设计响应系统 (27) 联合式(26)(27), 有 (28) u=kc(ep,z)=aep1-zep1+(c+1)ep2. (29) 其次,设计事件触发控制器.构造误差系统的快系统 (30) 其中kf(ef,z)=aef1-zef1+(c+1)ef2; 误差系统的慢系统 (31) 其中ks(es,z)=aes1-zes1+(c+1)es2. 构造辅助系统的Lyapunov函数 (32) 通过定理1中流集和跃集以及快慢系统的离散映射的设计, 可以确定事件触发控制率. 仿真中取快慢系统的初始状态分别为[1,9]T和[14,16]T. 选取快慢系统参数βf=2,βs=0.5.图2为驱动系统的状态相位图.由图2可见系统呈混沌现象.图3为事件触发控制器u的时间响应曲线.图4显示了误差系统Lyapunov函数Vp、辅助慢系统Lyapunov函数Vs和辅助快系统Lyapunov函数Vf的时间响应曲线. 由图3~4可见,Vp受边界约束影响在Vs与Vf构成的区域内演化;Vp在0.06 s左右达到Vs值触发事件, 致使系统在t=0.06 s时第一次更新控制率并作用于系统(11). 图5为分别在连续控制器和事件触发控制器作用下的驱动系统与响应系统间的误差信号. 由图5可见, 事件触发控制器作用下ep在约1 s后渐近收敛到0, 而连续控制器作用下ep在1.2 s后才渐近收敛到0, 表明本文所设计的事件触发控制器能更快地使系统同步. 图2 驱动系统的状态相位图Fig.2 State phase plot of the drive system 图3 控制输入信号Fig.3 Control input signal 图4 事件触发控制下的 Lyapunov曲线Fig.4 Graphical illustration of Lyapunov function under event-based control 图5 不同控制下误差系统状态的时间响应曲线Fig.5 Time response of the state of error system under different controls 图6显示了在本文所设计的事件触发控制下驱动系统状态与响应系统状态的时间响应曲线. 由图6可见,本文事件触发控制算法实现了驱动系统与响应系统之间的逐渐同步. 图6 驱动状态与响应状态的时间响应曲线Fig.6 Time responses of drive state and response state 本文针对异构混沌系统设计一种基于边界约束事件触发的控制器, 基于Lyapunov稳定性理论结合算法检测对系统的控制输入进行离散化更新,给出了异构混沌系统达到同步所需的条件. 本文所设计的控制器不仅使得驱动系统与响应系统达到同步状态,而且可通过设置辅助系统中快系统或慢系统的参数灵活改变边界Lyapunov函数形成的区域,从而改变异构混沌系统的同步速率.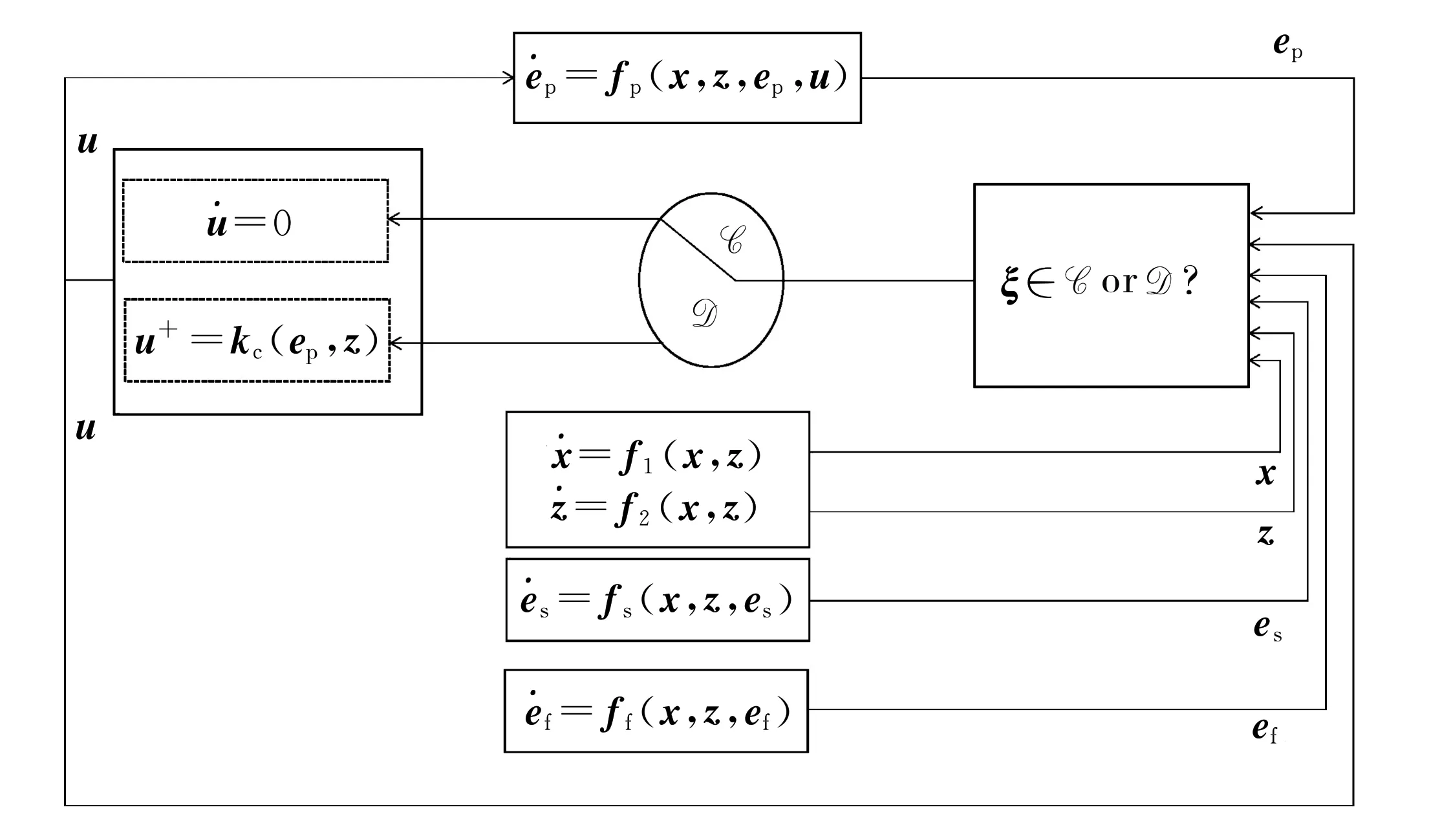
4 数值仿真
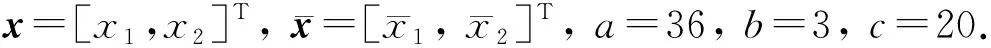
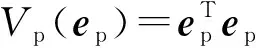

5 结语
