基于机器学习的铜期货价格预测分析

沈欣宜, 李 旭, 沈 虹

(扬州大学商学院, 江苏 扬州 225127)

一直以来, 金融资产的价格预测是微观金融领域关注的重要问题之一．传统的资产价格预测主要通过使用自回归、滑动平均、广义自回归等线性时间序列模型来实现．然而,由于资产价格的走势往往表现出高度的不确定性和非平稳的特征,因此,也大大限制了时间序列模型在价格预测方面的应用及拓展．近年来,随着人工智能的快速发展,以人工神经网络为代表的各类机器学习算法为构建数据间的非线性关系,提高预测能力提供了很好的思路与方法．在机器学习包含的众多学习算法中, 支持向量机(support vector machine,SVM)、神经网络等模型在价格预测方面有着广泛的应用．Huang等[1]使用SVM模型预测NIKKEI 225指数以及财务移动方向, 同时将SVM与线性判别、二次判别和Elman反向传播神经网络进行了比较,证明了SVM优于其他分类方法; Yu等[2]提出了一种演化的最小二乘支持向量机,探索美国股票市场三个重要股指的走势; Huang等[3]则采用支持向量回归(support vector regression, SVR)对单日股票价格的具体数值进行回归预测,通过特征选择方法优化输入特征,并运用自组织特征图(self-organizing feature maps, SOFM)技术对输入SVR的训练样本进行筛选,极大地提升了SVR的预测准确度．

神经网络作为人工智能领域的非线性方法,在处理多维、高频、非连续数据等方面具有先天优势, 且能有效识别金融序列的长短期记忆效应,因此被应用于各类金融预测．Di Persio等[4]将循环神经网络(recurrent neural network, RNN)、长短期记忆神经网络(long short-term memory, LSTM)和门控循环单元神经网络(gated recurrent unit, GRU)用于谷歌股价趋势预测, 结果显示LSTM 神经网络在金融序列预测方面具有优势; Fischer等[5]基于日度交易数据采用LSTM模型预测股票收益率相对于其截面中值的涨跌方向, 其构建的投资组合绩效显著优于传统线性模型; Zhang等[6]提出使用生成对抗网络来预测股票市场,并以多层感知机(multilayer perceptron, MLP)为鉴别器, LSTM为生成器来预测收盘价．

由于期货市场是一个复杂的非线性动力系统, 其价格波动受多重因素的影响．早期的相关研究主要从期货与现货之间、相同品种不同市场之间的高度相关性进行展开, 并基于市场本身的价量进行分析．以GARCH(generalized autoregressive conditional heteroskedasticity)模型、Copula模型为代表的时间序列模型是衡量价格波动的主流方法[7-8]．Yue等[9]采用VAR-DCC-GARCH模型探讨了中国有色金属市场价格和伦敦LME价格之间的Co-movement关系; Han等[10]从投资者情绪角度出发,分析其对价格波动的影响,研究发现基于Google搜索量构造的投资者情绪对商品期货价格具有较好的样本外预测能力．但如果将多重因素纳入同一价格预测框架中,传统的线性预测模型则变得越来越局限,而使用机器学习算法为期货市场价格预测研究打开了新的思路．基于此,本文拟以上海期货交易所的代表性品种铜期货为研究对象,对于影响铜期货价格的因素分析进行更为全面的分析．这个过程中往往充斥着各类噪音,并不是越复杂的机器学习算法就越有效,因此需要根据数据与预测目标的相关性进行数据处理、分类和合成,并根据模型的拟合度不断进行优化,从而选择更为精准的预测模型．与此同时,由于引起资产价格变动的因素众多,在收集并运用大量金融数据的过程中,机器学习经常会遇到维度灾难的问题,这往往会降低模型的预测能力,如何选择合适的特征变量是亟需解决的关键问题．因此,本文将国内外市场的各类相关指标,以及反映投资者心理情绪的百度指数加入预测框架中,从中提取关键特征变量,通过构建多因素的支持向量机、MLP神经网络、LSTM神经网络和GRU神经网络模型分别对铜期货价格进行预测,旨在为有色金属期货市场的金融预测提供可参考的模型,使得对资产价格影响因素的研究更加全面．

1 模型介绍

1.1 SVM模型

1.1.1 SVM

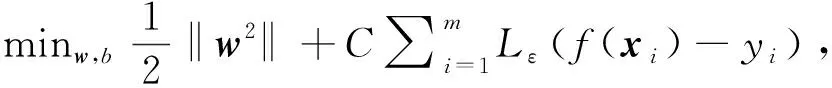
1.1.2SVR

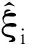
1.2 MLP模型

多层感知器(MLP)是一种前向反馈的人工神经网络, 由输入层、隐含层和输出层组成, 每层节点之间完全相连．输入层接收数据输入, 其他层的节点通过应用一个激活函数得到该层相应的输出．MLP的学习策略是使用梯度下降法,通过反向传播来不断调整节点间的权重和阈值,使网络的均方误差达到最小．图1是1个三层MLP神经网络模型示例．

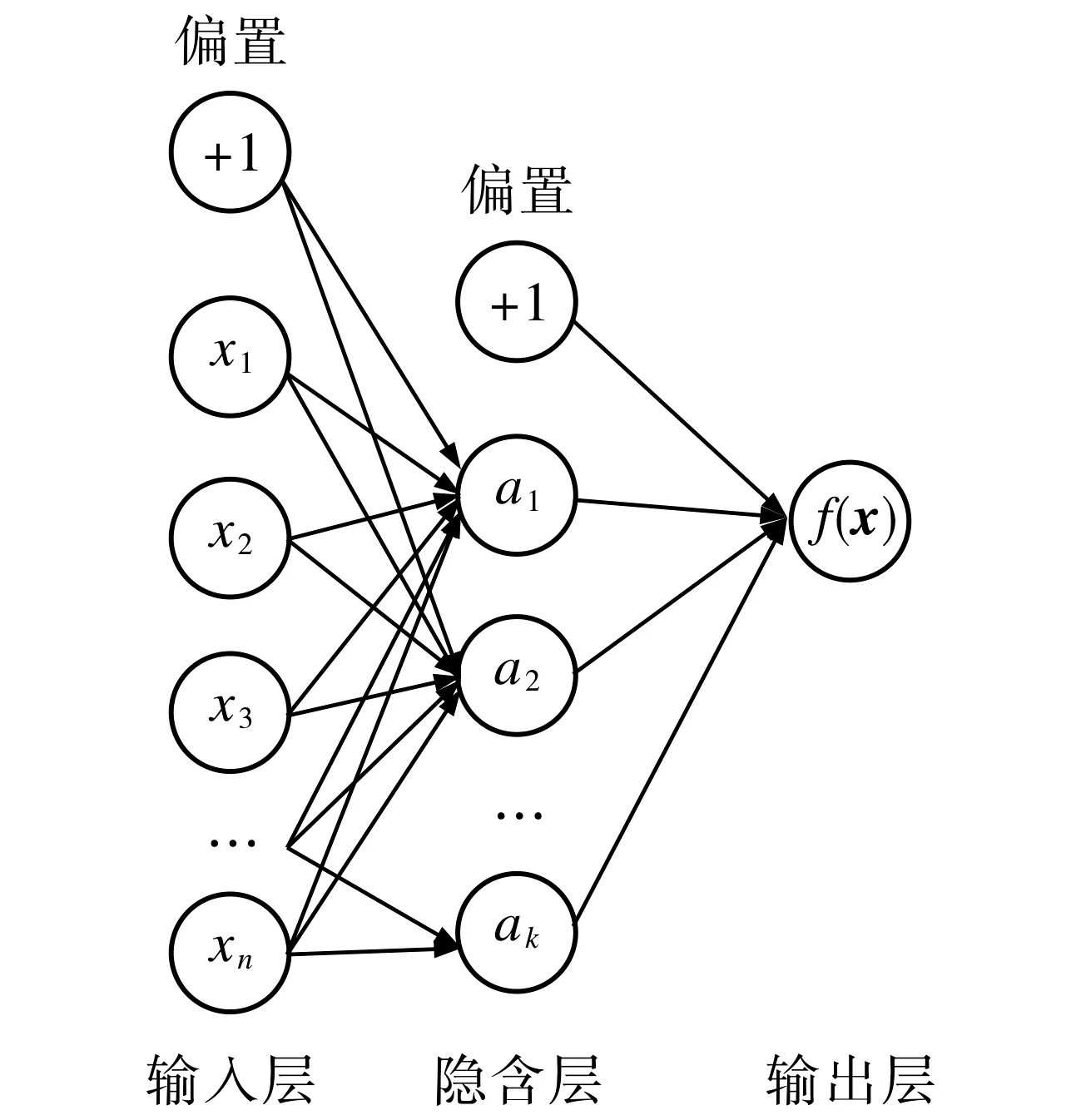
图1 MLP神经网络模型Fig.1 MLP neural network model

1.3 LSTM神经网络

LSTM神经网络是循环神经网络的一个变体, 通过设计特殊的神经元结构,能成功解决其他学习算法难以处理长期信息的缺陷．在细胞单元内部由三大门限单元构成, 分别是遗忘门、输入门和输出门, 如图2所示．LSTM的创新之处在于, 随着细胞元状态Ct-1从左至右贯穿LSTM结构, 序列数据首先经过遗忘门筛选掉部分信息,再通过输入门增加需要新增的数据, 而长期状态Ct直接输出．在LSTM结构的每个节点, 不断有数据筛选和增加,并且通过输出门结构,判断长期状态中哪些有效信息被保留, 哪些无效信息被过滤,形成短期状态ht．LSTM神经网络结构利用长短期序列数据共同学习, 将重要有参考性的信息保留在长期状态中,使模型达到最优．

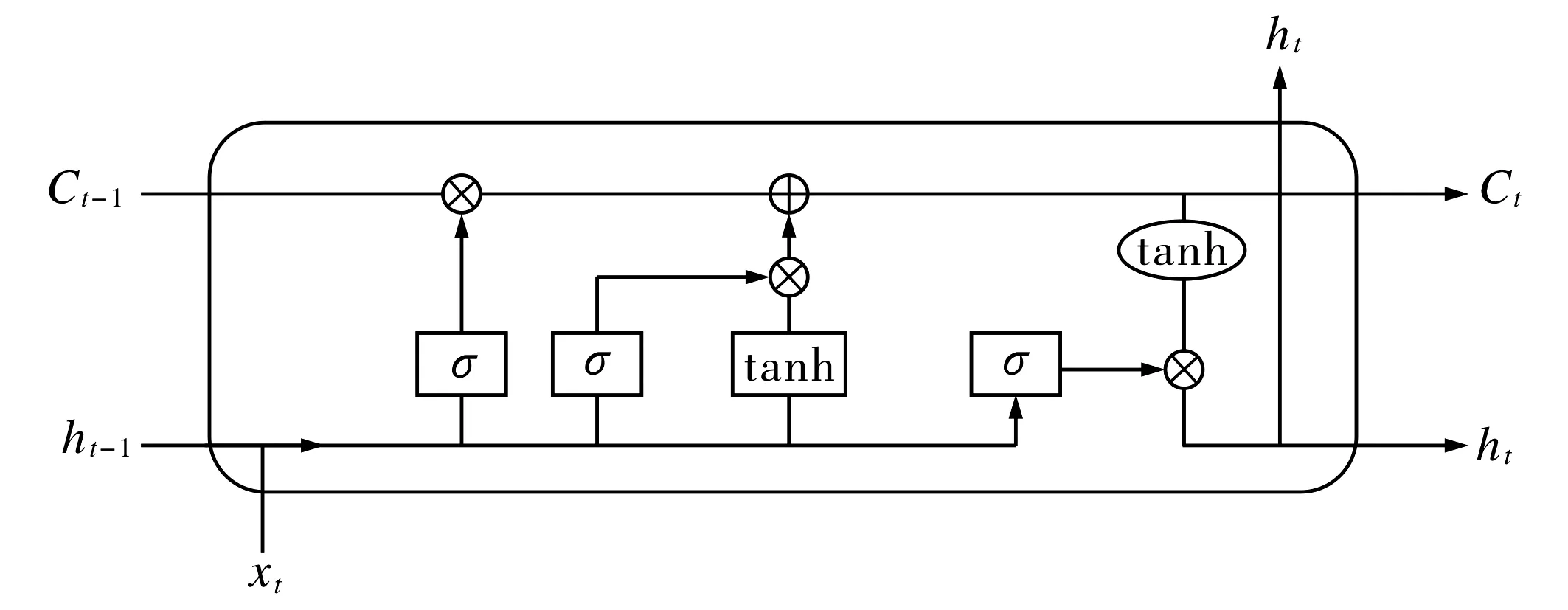
图2 LSTM网络结构图Fig.2 LSTM network structure diagram

1.4 GRU神经网络

GRU神经网络是循环神经网络的另一个重要变体．与LSTM相比, GRU结构更简单, 参数更少．GRU在LSTM基础上进行了2个改进: 1) 将输入门、遗忘门、输出门变为重置门rt和更新门zt; 2) 将LSTM的单元状态Ct与输出合并为一个状态ht．图3为GRU神经元的内部结构．

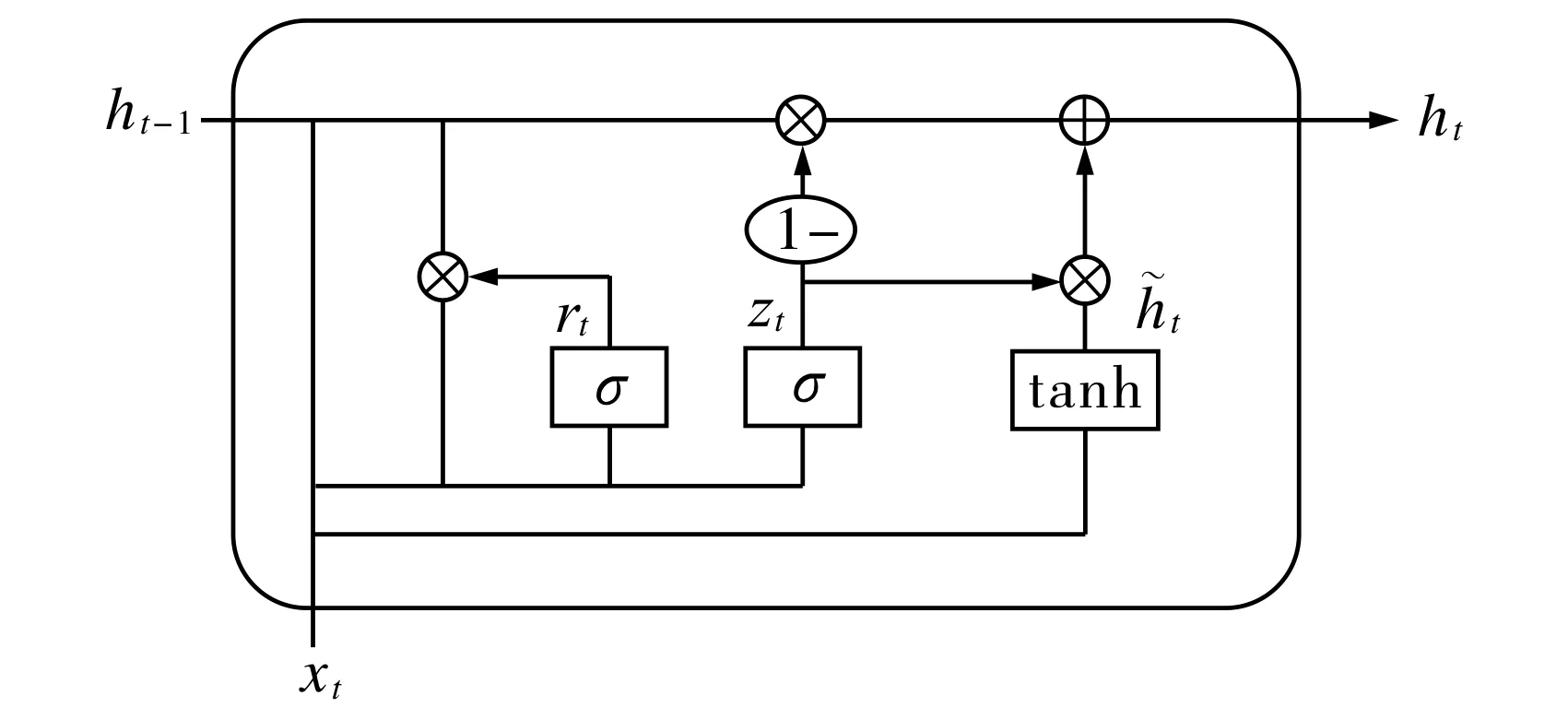
图3 GRU网络结构图Fig.3 GRU network structure diagram

2 数据预处理与变量选择

2.1 数据收集和预处理

2.1.1 指标选取

铜期货价格的波动除与历史价格相关外,还受到诸多因素的影响,主要包括供求关系、宏观经济、相关商品、国际期货市场以及市场情绪等．为了摆脱对历史交易价格的数据依赖,本文收集的数据中剔除了每日最高价、最低价、开盘价、收盘价,重点考察其他因素对铜期货价格的预测能力．由于期货结算价是某一期货合约每日按照交易量加权的平均价,其价格走势更具有代表性,因此,本文选取铜期货的结算价格作为被解释变量,将下一个交易日的铜期货结算价预测值作为模型输出,共选取26个指标,在供求关系方面选取铜期货的持仓量和成交量2个指标,其他24个指标按宏观经济、相关市场和百度指数分为三类,具体如表1所示．

2.1.2 数据收集

选取上海期货交易所铜期货的主力合约(简称“铜期货”)作为研究样本, 铜期货的结算价选取自2011年1月4日至2021年1月29日期间共2 452个日度交易数据, 其他26个变量的数据收集时间均是基于铜期货结算价时间序列．对于铜期货在当天有交易而其他变量没有交易或者出现数据缺失时,为保证数据的连续性, 用该序列的上一日有交易数据值进行填充．以上数据均来源于Wind数据库和百度指数官网．

为进一步细化预测效果,本文对有色金属进行长短期价格预测, 用20个交易日的时间长度衡量短期预测效果, 200个交易日的时间长度衡量长期预测效果．对预测模型训练时, 使用每个交易日的数据信息预测下一日的结算价, 故对总样本区间剔除最后20个交易日后的数据作为训练集, 分别选取最后200个交易日的前20和200个交易日数据作为短期和长期预测的测试集．

2.1.3 数据预处理

在建模过程中,为消除数据间的量纲影响并提升模型的预算速度, 对所有数据进行了零-均值规范化处理, 其转换公式为Z=(X-μ)/σ, 其中X为须要标准化处理的原始值,μ为均值,σ为标准差且不等于0．

2.2 变量选择

本次实验选取了26个特征指标, 从已有特征中筛选出与铜期货价格变动更相关的特征, 有助于提高模型预测的准确度[12], 因此在构建模型前, 须对原始特征变量进行选择和降维处理．

2.2.1 相关性分析

相关性分析用于衡量特征变量和目标变量之间的关系．Pearson相关系数是用来反映变量和变量的线性相关程度的一种方法, Pearson值介于-1和1之内, 绝对值的大小表示了相关性的强弱．X和Y两个相关变量间的Pearson相关系数r(X,Y)=E(X-μX)(Y-μY)/(σXσY), 其中μX和μY分别为X和Y的均值,σX和σY分别为X和Y的标准差,E为期望．

本文的输出变量为下一个交易日的铜期货结算价预测值, 为获得与输出变量相关性高的特征变量,首先测算26个特征变量与输出变量之间的Pearson相关系数, 其结果如表1所示．由于各特征变量在量级上有巨大差异, 所以本文在预测之前做了标准化处理来消除量级差异, 当r值低于0.5时表明特征变量和目标变量之间的线性相关性较低．由表1可知, 除了长江有色市场平均铜价、SHFE黄金持仓量、LME铜连续结算价、“伦铜期货实时行情”百度指数 、上期铜超额收益指数、上期铜期货价格指数这6个变量和下一日铜期货结算价之间存在较强的线性关系,其他20个变量都和目标变量线性关系较弱．这也说明期货结算价预测不适用线性模型．

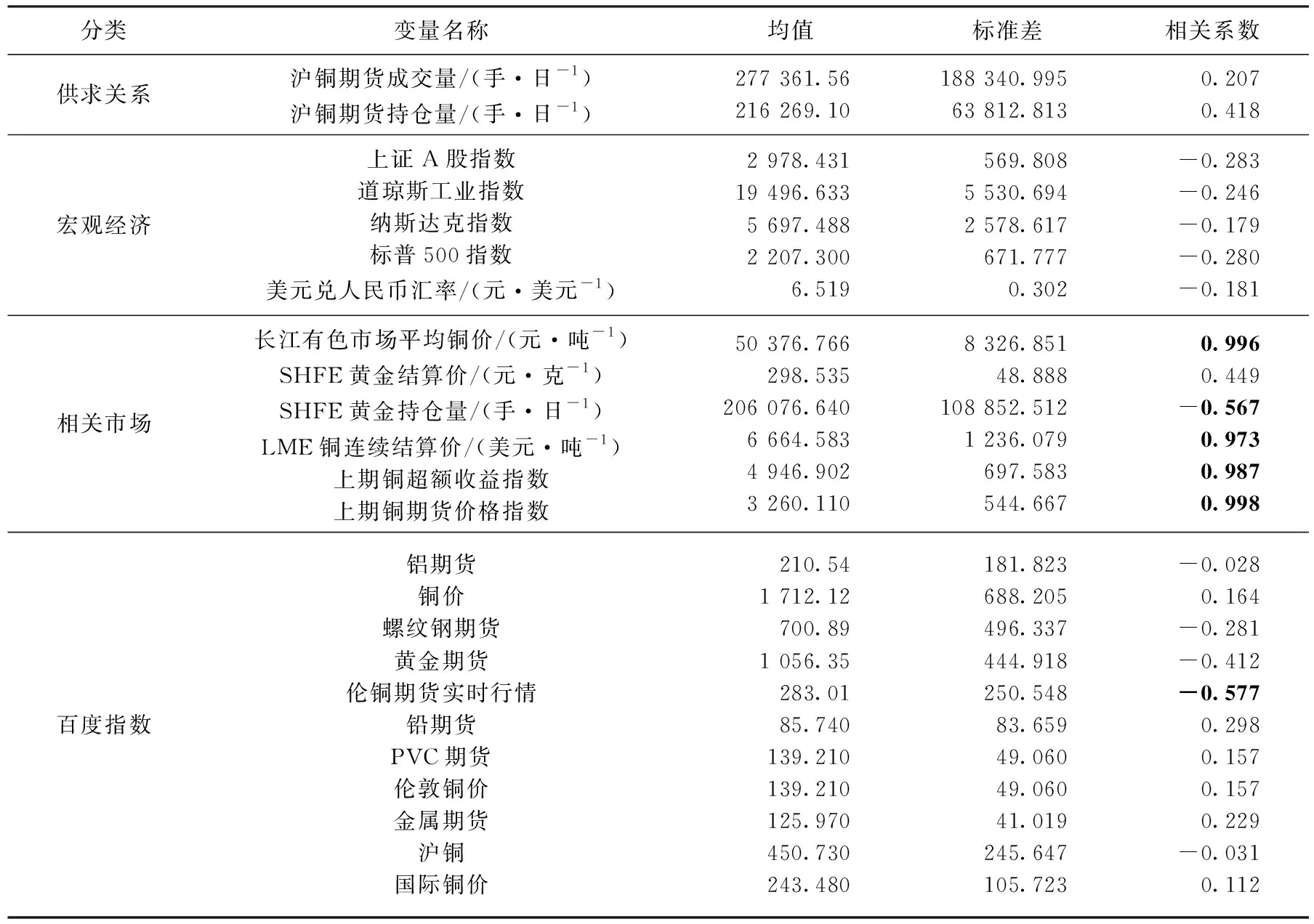
表1 输入变量的统计、分类以及与次日结算价的相关系数Tab.1 Statistics and classification of input variables and correlation coefficients with the next-day settlement price

2.2.2 主成分分析

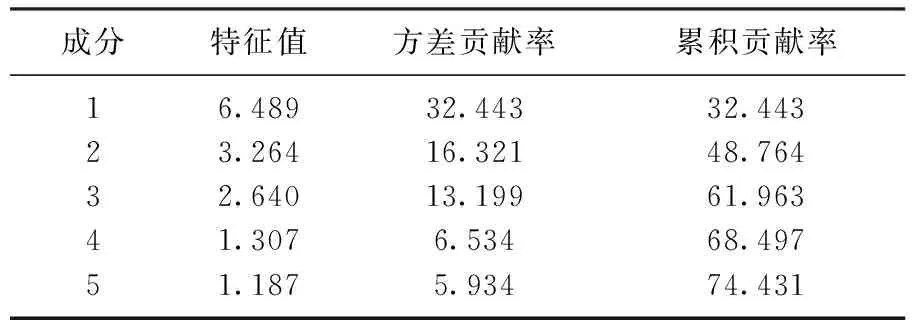
表2 主成分方差贡献Tab.2 Principal component variance contribution

由相关系数的分析可知,与下一日结算价相关系数超过0.5的6个变量可以作为输入变量放入模型中, 剩余20个变量虽然与被解释变量之间的线性关系较弱,但仍具有一定相关性,而机器学习模型输入变量个数较多时容易产生过拟合问题,故采用主成分分析法对剩余的20个解释变量进行降维处理．表2给出了部分主成分方差分析结果．根据表2的主成分方差分析结果并结合特征值大于1的原则,本文从中选用前5个主成分,其累积贡献率达到74.431%,表明前5个主成分已能较好地反映所有变量的信息．因此,本文共选取11个特征变量代入机器学习预测模型中进行价格预测,即6个强相关性变量和5个主成分变量．

3 铜期货价格预测效果分析

3.1 预测效果评估指数

3.1.1 回归法

3.1.2 分类法

对多种机器学习模型进行分类法预测时,将通过准确率、精确率、召回率以及F1值四大评价指标对预测结果进行评价．

1) 准确率．所有分类正确的样本个数占总样本个数的比例, 即准确率=分类正确的样本数/总样本数．准确率越大代表模型分类越准确, 但不能给出分类出错的类型和潜在分布, 故对于样本数据分布不平衡的情况, 准确率会受到大类别样本的影响．

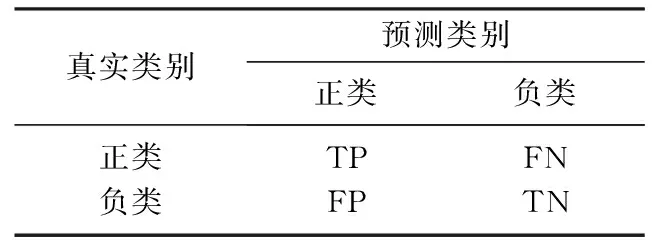
表3 混淆矩阵Tab.3 Confusion matrix

2) 精确度和召回率．可根据样本真实类别和分类器预测类别划分为四类判别矩阵, 如表3所示．精确率(P)是指所有分类正确的正样本数(TP)与所有预测为正类的样本数(TP+FP)的比值, 即P=TP/(TP+FP)．召回率(R)是指所有分类正确的正样本数(TP)与所有正样本数(TP+FN)的比值, 即R=TP/(TP+FN)．

3) F1值F=2PR/(P+R)中和了精确率和召回率的评估指标, F1值越高, 分类效果越好．

3.2 回归法下预测结果分析

以选取的11个特征变量作为模型输入, 在训练SVR 模型时, 通过对比线性核函数、多项式核函数和高斯核函数,最终选取线性核函数对沪铜期货进行分析．采用MLP神经网络预测时,设定隐藏层神经元数为8个, 模型训练的轮数为500,一个批次的大小设为80．经过多次测试和调优, LSTM和GRU模型的优化器选择AdamOptimizer, 损失函数使用MAPE, 学习率设为0.000 6, 每个隐藏层中神经元数均为10个．在模型优化方面,采用梯度下降方法, LSTM和GRU模型中一个批次的大小分别设为70, 60, 模型训练的轮数均为500．为了控制过拟合现象, 模型中加入dropout结构, 并将dropout的数值设为0.2．图4为不同机器学习模型对铜期货价格预测的走势图，表4为上述四种机器学习模型在测试集上的预测结果．结果显示, 四种机器学习模型不论是在长期预测还是短期预测中, 对铜期货结算价格的预测结果都很稳定, 且各模型长期预测和短期预测的结果相差不大; 因此, 在摆脱对价格交易数据的依赖后,根据引入的相关影响因素进行机器学习对铜期货价格有较好的预测能力, 而四种机器学习模型能够在预测中得到相似的预测结果, 表明机器学习在铜期货结算价格预测中的适应性很强．

表4 各模型回归法预测结果Tab.4 Prediction results of regression methods %

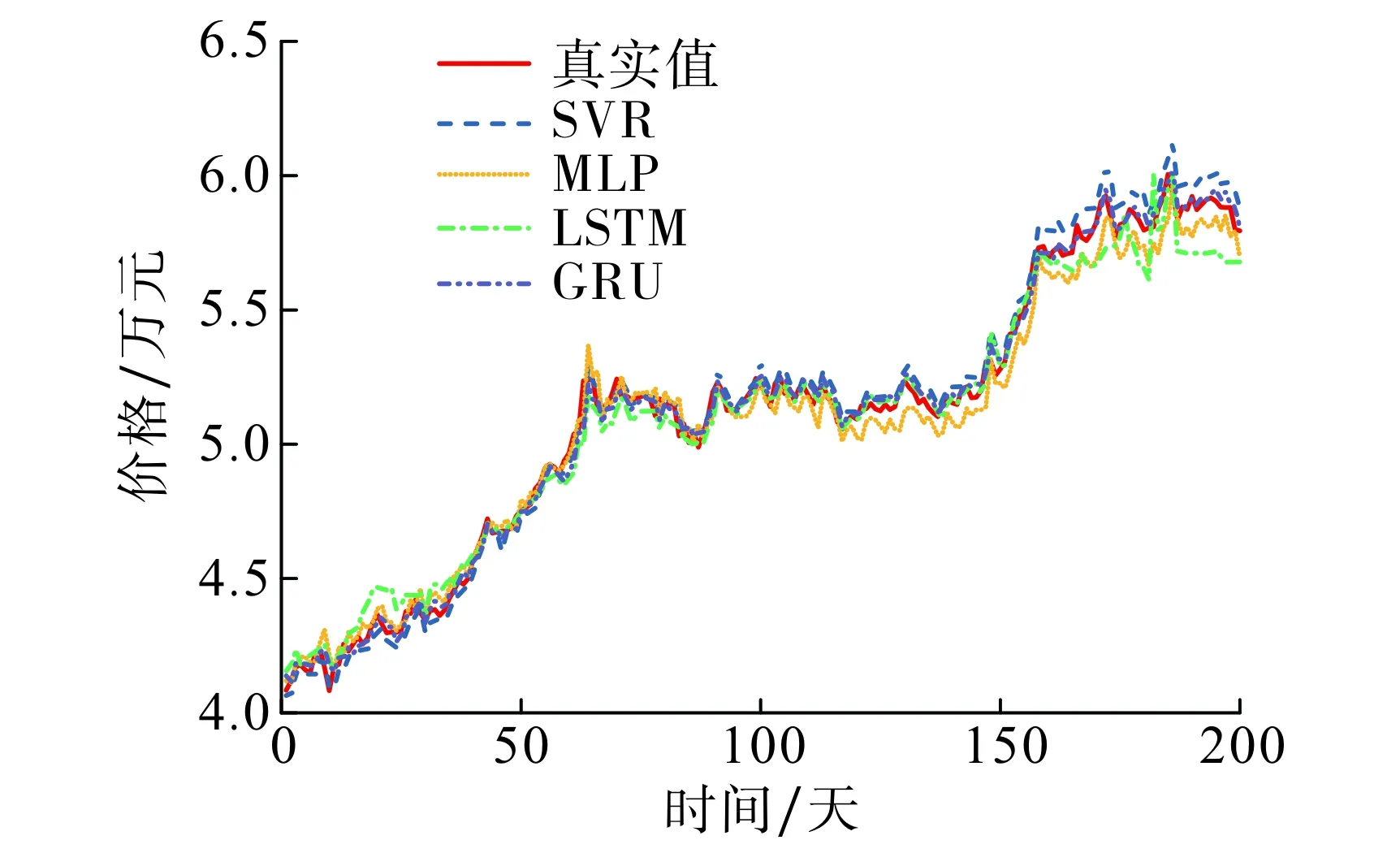
图4 不同机器学习模型下铜期货 价格预测走势图(200日)Fig.4 Forecast trend of copper futures price under different machine learning models (200 days)

3.3 分类法下预测结果分析

四种机器学习模型利用分类法实现对铜期货价格涨跌的预测时, 本文将铜期货结算价格涨跌预测问题转化为二分类问题: 当本日结算价大于前日结算价时, 判定为本正样, 即价格上涨, 用1表示; 反之, 则判定为负样本, 即价格下跌, 用0表示, 并利用选取的11个特征变量对下一日的铜期货结算价格的涨跌进行预测．以LSTM模型对20日的预测为例, 当LSTM模型预测的准确率达到0.85时, 表示对20个交易日的涨跌行情, LSTM模型准确地预测了17个交易日的涨跌情况．对实验结果调查发现, LSTM模型准确预测了14个正类样本中12个, 6个负类样本中5个, 故其精确率为12/(12+1)=0.92, 召回率为12/(12+2)=0.86．

表5给出了分类法预测结算价的结果．由表5可知, 在对铜期货价格的短期预测中, LSTM和GRU模型的四项指标均表现的较为突出,而SVM和MLP模型的预测效果稍逊．然而在对铜期货价格进行长期预测时, 四种机器学习模型的预测效果相差不大, 仅出现SVM的召回率相对较优异的结果．

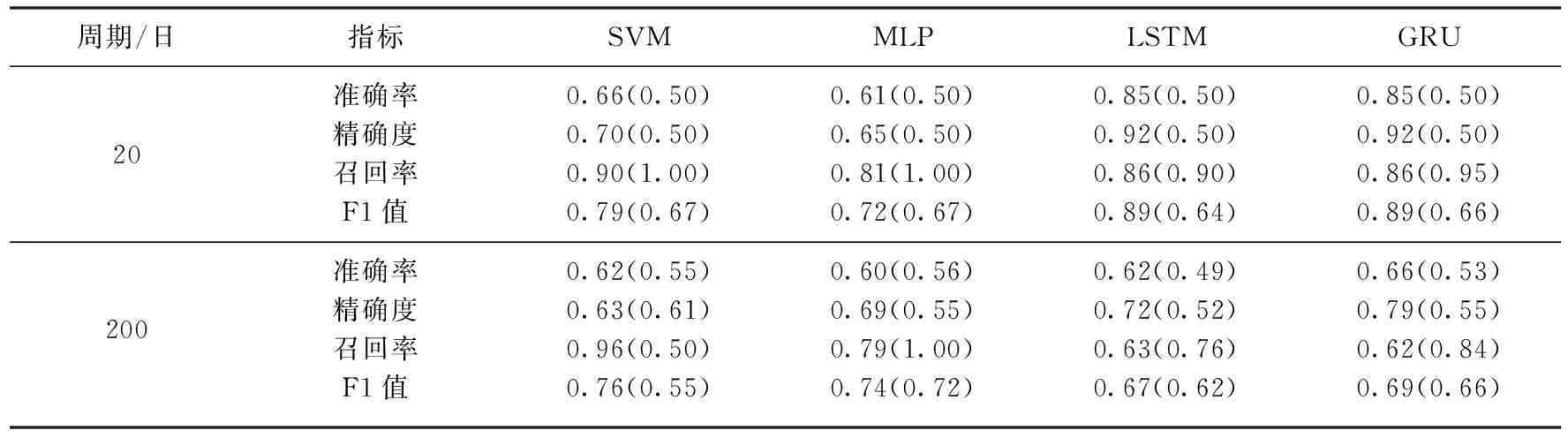
表5 分类法预测结算价Tab.5 Predicting settlement prices under classifications

4 结论

1) 摆脱对交易数据的依赖后, 被引入的多因素指标通过机器学习能够对铜期货价格有较好的预测能力; 2) SVM、MLP、LSTM、GRU四种机器学习模型能够在预测中得到相似的预测结果, 表明机器学习在铜期货价格预测中有很好的适用性．

当然, 金融资产价格的变化除了受可度量经济指标的影响外,往往还受其他不可量化的因素影响,如政策环境、突发事件等．同时,本文中超参数的调试是人工调参,并且一些超参数的选取是参考的已有经验,如果可以借助自动调参工具使调参过程更加简化,同时减少人为调参的主观影响,那么预测模型的选择将更加精确与合理, 这将是本课题组进一步研究的方向．