预测胶粉改性沥青混合料的相位角并分析其粘弹性*
2022-01-14张飞,王岚,李超,刘恒
张 飞,王 岚,李 超,刘 恒
(1.内蒙古自治区土木工程结构与力学重点实验室,呼和浩特 010051;2.内蒙古工业大学 土木工程学院,呼和浩特010051;3.内蒙古自治区交通运输科学发展研究院,呼和浩特010051)
0 引 言
沥青混合料粘弹性原理的应用受到越来越多的关注。沥青混合料粘弹性的表征包括测量混合料的强度及弹性和粘性的相对比例[1]。粘弹性材料的力学行为与温度、频率、加载历史都密切有关[2-3]。因此研究沥青混合料性能关于温度、频率的依赖关系对了解沥青路面的工作性能非常重要。在小应变范围或有限次数的循环荷载作用下,沥青混合料表现出线性粘弹特性[4-5]。复数模量试验是研究沥青混合料的线性粘弹性最常用的方法。在线性粘弹性范围内,沥青混合料的动态模量和相位角仅依赖于温度和频率。其中沥青混合料的动态模量是沥青路面结构设计的重要参数之一。AASHTO 2002年出版的《路面设计指南》中就指出动态模量是沥青混合料的一个最基本参数,它代表了材料的刚度性能,其大小随温度和频率的变化而变化。根据力学-经验设计方法(MEPDG),动态模量所反映的信息和性能参数比其他参数更适合于路面设计。目前已经发展了很多用于测试动态模量的方法[6],例如重复加载法、无约束共振法及瑞利波分析法,考虑到单轴压缩法(属于重复加载法)是目前应用最普遍的试验方法,因此本文也采用这一方法进行胶粉改性沥青混合料动态模量的测试。此外已经建立的多项式模型[7]、标准对数Sigmoidal模型[8]、广义对数Sigmoidal模型[9-10]等都可用以表征沥青类材料的动态模量主曲线。很多文献表明[11-12],非对称的广义对数Sigmoidal公式比对称的Sigmoidal公式更能代表动态模量主曲线,因此本文也选择广义对数Sigmoidal公式作为胶粉改性沥青混合料动态模量主曲线的函数形式。然而受实验设备及其他因素的限制,相位角的测量难免会出现偏差,有时甚至难以获得测试数据(例如长寿面路面)。因此建立相位角与动态模量的函数关系就显得尤为重要,基于此Dickersen和Wit[13]提出了沥青胶结料的相位角、复模量和频率之间的关系,然而这样的表达形式分别采用独立的参数构建函数关系,导致其结果往往难以满足Kramers-Kronig(K-K)关系[14];Christensen和Anderson[15]通过动态热机械分析(DMA)的结果提出了描述沥青类材料粘弹性力学行为的经验性算法公式,即Christensen-Anderson(CA)模型,然而该模型对改性沥青胶结料显得无能为力;Marasteanu and Anderson[16]通过改进CA模型开发了一个新的模型(即CAM模型),以改善CA模型在低区和高区的频率范围拟合不准确的问题,然而该模型在预测主曲线二端的渐近线时精确度略有不足且对沥青混合料显得无能为力。为解决复数模量及相位角难以满足K-K关系的问题。Booij和Thoone[17]提出了基于广K-K关系由复数模量与频率的斜率预测相位角的概念。Marasteanu and Anderson在建立CAM模型的过程中[16]也借鉴了这一方法。同样的为实现混合料相位角主曲线的预测,根据Booij和Thoone的成果,Rowe[19]提出基于Sigmoidal模型的沥青混合料相位角主曲线的函数形式。Mensching[19]利用同样的方法构建了基于广义Sigmoidal模型的相位角主曲线函数形式,并利用Black Space参数来评价沥青混合料的低温性能。Liu[20]也使用这样的方法构建了满足K-K关系的高精度复数模量主曲线。Nobakht[21]使用同样的方法预测了九种老化条件下混合料的相位角,结果表明该方法对老化后的混合料同样可行。所有这些研究结果都表明由动态模量预测相位角的可行性。尽管目前胶粉改性沥青混合料高低温性能的研究成果已有很多,然而同时从松弛模量和蠕变柔量的角度研究温拌前后胶粉改性沥青的线性粘弹性的研究成果并不多见。本文通过时间-温度叠加原理[21],在满足K-K关系的基础上构建了温拌胶粉改性沥青混合料的广义Sigmoidal动态模量主曲线。根据近似K-K关系由斜率法从动态模量主曲线预测了相应的相位角主曲线,在此基础上进一步计算时域的松弛模量和蠕变柔量,用以分析温拌前后胶粉改性沥青混合料在线性粘弹性范围内的松弛及蠕变特性,从而研究相应混合料的高低温性能。
1 实 验
1.1 材料和试样制作
本研究制备了二种类型的温拌胶粉改性沥青混合料作为对比同时也制备了相应的热拌混合料。混合料级配类型为AC-16。基质沥青性能等级为PG 64-22,将60目胶粉和混合目胶粉分别加入到基质沥青中,按照适当工艺[23]即可制备出对应的胶粉改性沥青,其中橡胶粉与基质沥青的质量比为1∶5。温拌剂为SDYK型表面活性剂且其掺量为胶粉改性沥青质量的1%。表1和图1为混合料的矿料级配,此外HMA-60和HMA-C中胶粉改性沥青含量分别为5.4%和5.6%。温拌沥青混合料中的胶粉改性沥青含量与相应的热拌沥青混合料相同。热拌混合料的拌和温度、压实温度分别为180、170 ℃,而温拌混合料的拌和温度、压实温度分别为162和152 ℃。温拌混合料的体积参数与相应的热拌沥青混合料的体积参数一致,表2为各类混合料的体积参数。采用Superpave旋转压实仪制作直径为150 mm,高度为178 mm的原始试样,然后取芯、切割,制备出直径100 mm,高度150 mm的标准试验试件。试样的空隙率控制在3.5%~4.5%之间。为降低老化所有试样均保存在无光的养护箱中,但不宜超过两周。

图1 胶粉改性沥青混合料的级配

表1 各档集料掺配比例

表2 最佳沥青用量下的体积参数
1.2 实验方案
根据AASHTO TP 79-15[24],进行压缩载荷下复数模量试验。利用伺服液压万能试验机(UTM-100)进行动态模量和相位角的测试。试验温度为5、20、35、50 ℃,荷载频率为25、20、10、5、1、0.5、0.1 Hz。试验从最低温度(5 ℃)开始到最高温度(50 ℃)终止。并对每个试样进行了从最高频率(25 Hz)到最低频率(0.1 Hz)的扫描测试。为了保证试样在线性粘弹性范围内,最大轴向应变不宜超过125 με[24]。
2 粘弹性响应函数的计算方法
2.1 移位技术
Williams,Lanedl,Ferry等人在研究高分子材料的时间、温度依赖关系过程中找到了移位因子的经验表达式[25],即WLF公式。它可在Tg~Tg+100 ℃的温度范围内表达移位因子对温度的依赖关系。公式1就是WLF公式的函数表达形式。本文也采用WLF公式计算移位因子。
(1)
其中:lgαT为移位因子;C1、C2为WLF公式的经验常数;Tr和T分别为参考温度和实验温度,℃。
2.2 动态模量主曲线模型
动态模量可由复数模量试验来获得,复数模量可由施加的半正弦应力σ(t)与其对应的应变ε(t)之比来定义,详见公式2。复数模量的绝对值就是动态模量,在试验测试过程中动态模量可由峰值应力与峰值应变之比来定义,详见公式3。而复数模量试验中应变滞后于应力的相位差就是相位角[26],在试验测试过程中可由最后5次加载循环中峰值应力和峰值应变的平均滞后时间与最后5次加载循环的平均加载周期之比来定义,详见公式4。对弹性材料,相位角等于0 °;对粘性材料,相位角等于90 °;对粘弹性材料,相位角在0 °~90 °范围内变化[27-28]。
(2)
(3)
(4)
其中:E*是复数模量,MPa;σ0是峰值应力,MPa;ε0是峰值应变;ω是角频率,rad/s;φ是相位角,°;ti是最后5次加载循环中峰值应力和峰值应变的平均滞后时间,s;tp是最后五次加载循环的平均加载周期,s。
通过将实测动态模量数据点移动到参考温度,形成一条平滑的曲线,即动态模量主曲线。它可用来研究沥青混合料在较大范围的动态粘弹性力学性能。本文以20 ℃作为参考温度。大量研究表明[29-30],当加载频率趋于无穷,动态模量趋于最大值,当加载频率趋于零,动态模量趋于最小值。广义Sigmoidal主曲线模型可以很好的表征这一特性。
与Sigmoidal模型相比,广义Sigmoidal模型增加了控制模型非对称特性[31-32]的参数λ。其计算表达形式见式(5)。
(5)
式中:δ是主曲线的下端近似值;α是主曲线的上端近似值与下端近似值之差;β,γ,λ是主曲线的形状系数,参数γ影响最大值和最小值之间的变化率,参数β影响转折点的水平位置,参数λ影响曲线的非对称特性;fr是缩减频率,Hz。
缩减频率是实验温度对参考温度的等效频率,在对数坐标下可按公式6进行计算。
lgfr=lgf+lgαT
(6)
式中:fr为任意试验温度相对于参考温度的缩减频率,Hz;f为试验频率,Hz。
2.3 相位角主曲线模型
Booij和Thoone[17]根据广义Kramers-Kronig关系提出相位角可由复数模量与频率的函数关系(斜率方法)来获得,如式7所示。但该式在计算过程中存在极大的困难。为便于计算,对公式进行适当的简化,得到基于近似Kramers-Kronig关系[33-34]的简化计算公式,如公式8所示。将广义Sigmoidal模型的函数形式代入公式8可以得到基于广义Sigmoidal模型预测的相位角函数形式,公式9即为由广义Sigmoidal模型按照近似Kramers-Kronig关系得到的相位角表达形式。在实际应用过程中考虑到相位角较大的变异性,因此在相位角的预测函数形式中习惯性的引入调整参数k,通常用公式10来代替公式9[35]。本文也采用公式10进行相位角的预测。
(7)

(8)
(9)
(10)
其中:u是积分变量;φ(fr)是基于近似K-K关系由动态模量主曲线预估的相位角,°;φ1(fr)是基于广义Sigmoidal动态模量主曲线预估的相位角,°;k是相位角的调整参数。
2.4 确定动态模量主曲线和相位角主曲线的模型参数
根据广义Sigmoidal模型分别构建了4种沥青混合料的动态模量主曲线,并采用WLF公式计算移位因子。广义Sigmoidal动态模量主曲线模型有5个待定的模型参数(δ、α、β、γ、λ),此外,尚需确定移位因子参数(C1、C2)和相位角的调整参数(k)。将动态模量和相位角的测试数据代入误差函数ef,同步求解公式5和10即可获得模型所有参数及相应的移位因子参数。误差函数ef的表达式详见公式11。所有的模型参数、移位因子参数及相位角的调整参数都可以通过非线性最小二乘回归得到[36]。最终将所得的参数拟合结果列于表3。
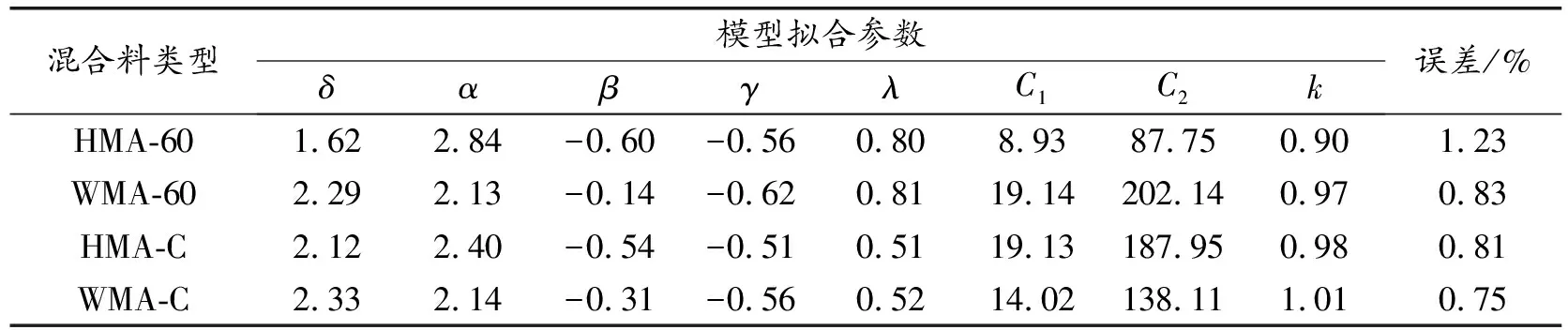
表3 广义Sigmoidal模型的拟合参数

(11)
其中:ef是误差函数,%;N是试验测试数据点的个数,其大小等于28;|E*|m,i是实测动态模量的第i个数据点,其数值可由复数模量试验直接获得,MPa;|E*|p,i是动态模量的第i个预测点,其数值可从公式5求得,MPa;|φ|m,i是实测相位角的第i个数据点,其数值可由复数模量试验直接获得,°;|φ|p,i是相位角的第i个预测点,其数值可从公式10求得,°。
从表3的模型参数拟合结果可知,参数λ都不等于1,这就说明胶粉改性沥青混合料的主曲线确实是非对称的,此外模型的最大误差仅有1.23%,这就充分说明了与实测结果相比,动态模量和相位角的模型预估值都显示出较高的相关性,这也进一步说明了预测模型的可靠性。
3 结果和讨论
3.1 移位因子的比较
将表3中的移位因子参数代入公式1即可求出相应的移位因子。图2为4种混合料在不同温度下的对数移位因子结果。由图可知,移位因子是温度的函数,当试验温度大于参考温度时移位因子小于1且温度越高移位因子越小,反之当试验温度小于参考温度则移位因子大于1且温度越低移位因子越大。在参考温度下4种混合料的移位因子都等于1,当试验温度大于或小于参考温度不同类型混合料的移位因子也不同,具体表现为HMA-60的移位因子大于其他3类混合料的移位因子,这说明HMA-60温度敏感性最高;温拌后HMA-60的移位因子减小而HMA-C的移位因子变化并不显著,说明温拌后降低了HMA-60的温度敏感性。

图2 胶粉改性沥青混合料的移位因子
3.2 动态模量预测结果与实测结果的比较
图3在双对数坐标下绘制了4种沥青混合料的实测值和广义Sigmoidal模型的预测值,图中对角线是动态模量的等值线。由图可知当频率较高即动态模量较大时(>1 000 MPa)数据点均匀地分布在等值线上,与等值线具有极好的线性线相关性;当频率较低即动态模量较小时(<1 000 MPa)数据点在等值线附近略有波动,且HMA-60的离散型最为显著;尽管如此,但所有混合料的动态模量预测值与实测值的相关系数都高达0.999,这说明四类混合料的模型预测值与实测值都显示出极高的线性相关性。也就是说基于K-K关系的主曲线拟合并没有以牺牲动态模量的精确性为代价,这也进一步说明广义Sigmoidal模型可作为胶粉改性沥青混合料的动态模量主曲线的预估模型。
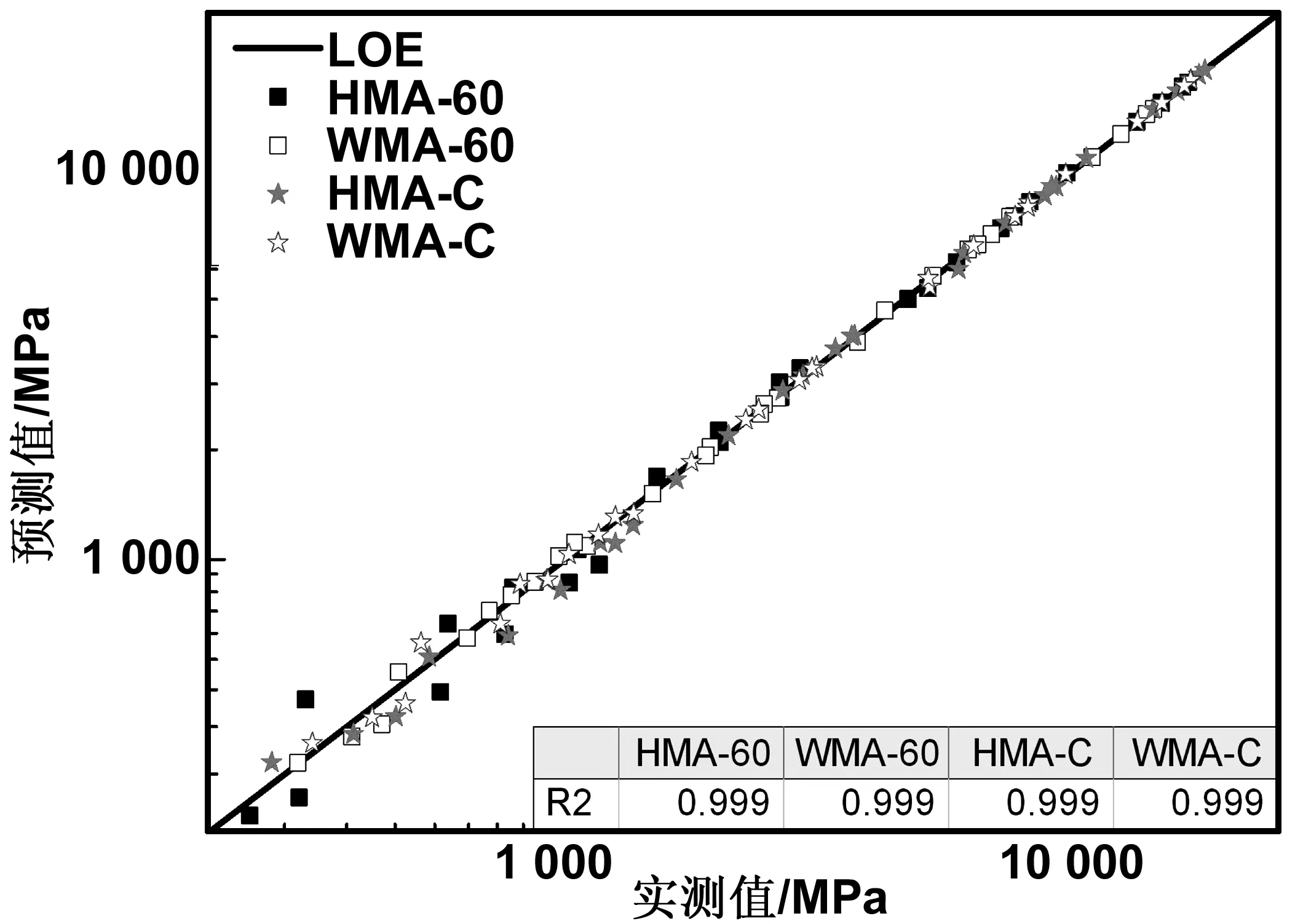
图3 动态模量预测结果及其实测结果的比较
3.3 相位角预测结果与实测结果的比较
根据斜率方法可从动态模量主曲线得到相位角与频率的函数关系。将表3中的模型参数结果代入公式10,即可得到相位角的预测结果,且这样的结果满足K-K关系,并将不同混合料的预测结果与实测结果都绘制于图4。
图4是基于广义Sigmoidal模型的斜率法构建的不同混合料的相位角主曲线预测结果及其实测结果。图中对角线是相位角的等值线,由图可知所有数据点均匀分布在等值线二侧,这说明与实测结果相比基于广义Sigmoidal主曲线预测的相位角主曲线具有较好的拟合优度。此外也发现HMA-C的拟合优度最好高达0.978,而WMA-60的数据点分布较为离散拟合优度仅为0.884.这也说明相位角预测值的拟合优度远不如动态模量,这一方面是由于相位角主曲线是从动态模量主曲线按照近似K-K获得,这一过程本身就存在误差,另一方面是因为相位角实测结果本身就存在较大的变异性[37],尤其是高温下,相位角的变化性较为显著。
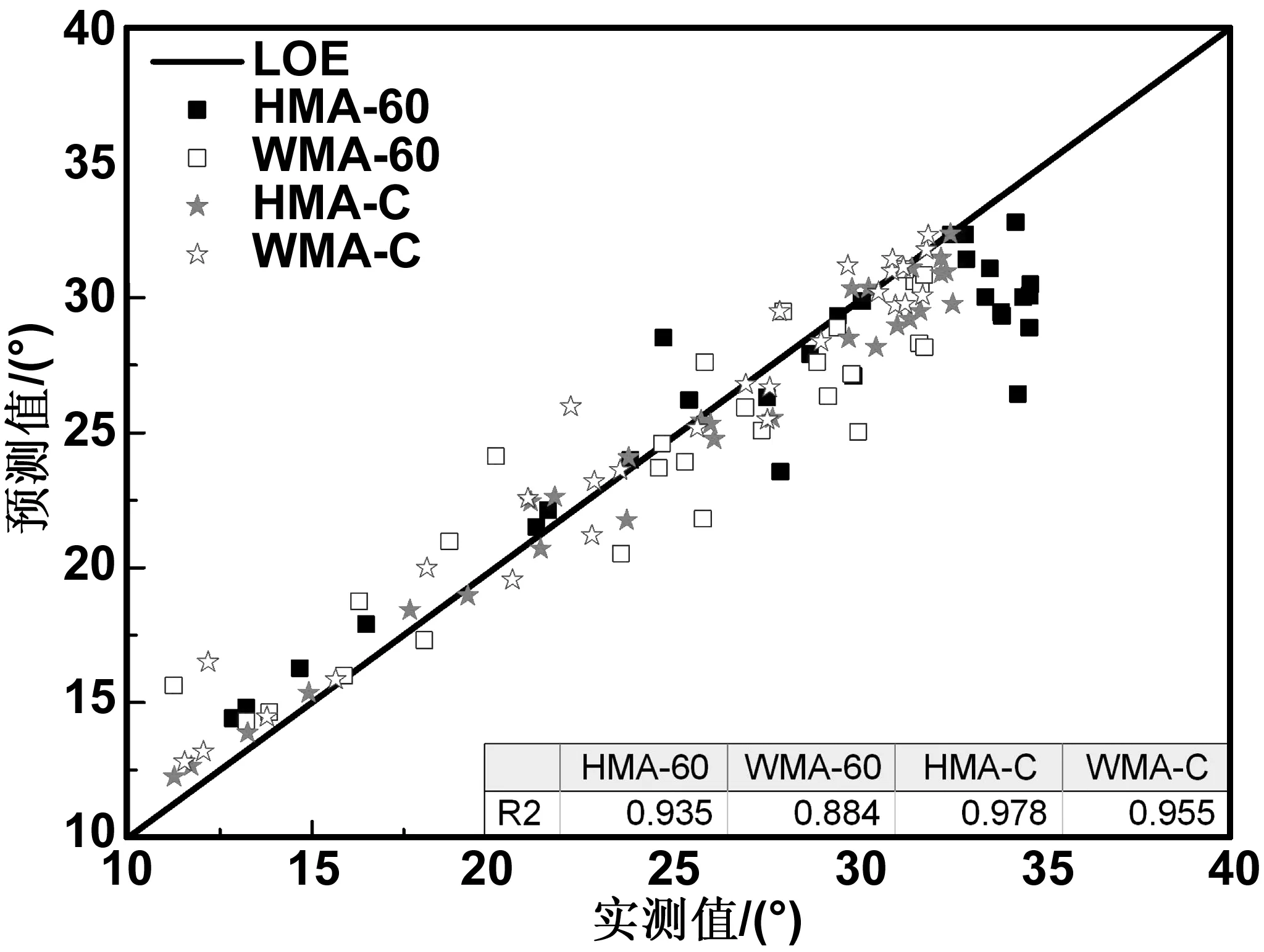
图4 相位角预测结果及其实测结果的比较
3.4 用Black Space图验证动态模量和相位角主曲线符合线性粘弹性理论
Black Space图[38]是将动态模量和相位角以半对数曲线图的形式绘制出来。为增强对比在此将动态模量和相位角的实测值及预测值都绘制于同一张Black Space图,并用以检查预测模型的可靠性。图5是HMA-C和WMA-C的Black Space图。在该图中,由广义Sigmoidal模型得到动态模量的预估值,根据K-K关系由斜率法得到相位角的预估值。结果表明,所有的数据点都位于或接近于一条独特的平滑曲线,该结果既证明了实测结果的可靠性,也验证了所构建的动态模量和相位角主曲线符合线性粘弹性理论。此外如图6所示,这样的结果也在Cole-Cole图[39]得到了证明。其他类型的胶粉改性沥青混合料也表现出类似的规律,考虑到文章篇幅有限,这里不做进一步论述。

图5 Black Space图

图6 Cole-Cole图
3.5 不同类型胶粉改性沥青混合料动态模量及其相位角主曲线的比较
为便于比较不同类型混合料的动态模量及其相位角,将4种胶粉改性沥青混合料的动态模量主曲线和相位角主曲线都显示于图7,其中采用广义Sigmoidal模型构建动态模量主曲线,根据近似的K-K关系,得到对应的相位角主曲线。
由图7可以看出,动态模量主曲线呈现S型,相位角主曲线呈钟形。比较4种混合料的动态模量主曲线发现,HMA-60的动态模量总是比HMA-C的动态模量小;但加入温拌剂后,混合料的动态模量在高频域变小,低频域变大,且对HMA-60的改变比HMA-C更加显著;WMA-60的动态模量总是比WMA-C的动态模量小。这样的结果表明,HMA-C的抗变形能力比HMA-60强;一旦加入温拌剂,混合料在低频下(高温)的抗变形能力增大,高频(低温)下的抗变形能力减小;WMA-C的抗变形能力也优于WMA-60。比较4种混合料的相位角主曲线发现,HMA-60的相位角始终大于HMA-C的相位角;加入温拌剂,混合料在高频的相位角变大,低频的相位角变小。这进一步表明,HMA-C的粘性成分占比小于HMA-60;一旦加入温拌剂,沥青混合料的粘性成分占比在低频区(高温)减小,在高频区(低温)增加。这主要是由于同等条件下混合目胶粉改性沥青胶结料的粘度大产生的混合料粘聚力也大,同时混合料在压实过程也需要提供更大的压实功,导致混合目胶粉改性沥青混合料具有更高的强度和更好的抗变形能力;温拌后降低了混合料的拌和温度,这在一定程度上也减小了胶结料的老化,导致胶结料具有更好的流淌性,更多的胶结料可以被集料吸收从而提高结构沥青含量而减少自由沥青含量,最终表现出温拌后混合料的强度也在一定程度上有所提高。从分子角度看,这是由于温拌后混合料中的沥青胶结料的分子量和极性官能团的浓度都下降导致的[40]。

图7 胶粉改性沥青混合料的动态模量及其相位角主曲线
3.6 胶粉改性沥青混合料的松弛和蠕变特性
存储模量和损失模量是组成复数模量的2个关键部分[41],确定了不同温度和频率下的动态模量和相位角之后,可以根据公式12和13分别得到相应的存储模量和损失模量。而存储模量和损失模量又是计算松弛模量和蠕变柔量的重要参数。
E′=|E*|cos(φ)
(12)
E″=|E*|sin(φ)
(13)
其中:E′是储存模量,MPa;E″是损失模量,MPa。
3.6.1 胶粉改性沥青混合料的松弛特性
在温度和车辆荷载作用下,沥青路面结构的内应力会随着时间的增加而逐渐消散,即产生应力松弛[42]。当温度较低时,沥青路面的松弛能力较差,路面结构存在大量的应力积累,易引起开裂,松弛模量[43]是评价松弛能力的最重要指标,因此有必要研究沥青混合料的低温松弛模量。根据粘弹性材料函数与算子函数的关系[44],可得到用Prony级数表示的存储模量和损失模量,见式14、15。
(14)
(15)
其中:E′(w)是用缩减角频率表示的存储模量,它按照公式12由相应角频率下的动态模量和相位角的余弦来获得,MPa;E″(w)是用缩减角频率表示的损失模量,它可按照公式13由相应角频率下的动态模量和相位角的正弦来获得,MPa;Ee是长期平衡模量,MPa;Ei是松弛强度,MPa;ρi是松弛时间,s;w是缩减角频率,其大小等于2πfr。
为得到长期平衡模量和松弛强度。需要同步求解公式14和15,因此这里引入误差函数ef1。误差函数ef1可表示为公式16的形式,其中松弛时间可以按照Park[44]提供的方法在对数时间轴上以等距取值,其计算结果详见表4。计算过程可参考误差函数ef。
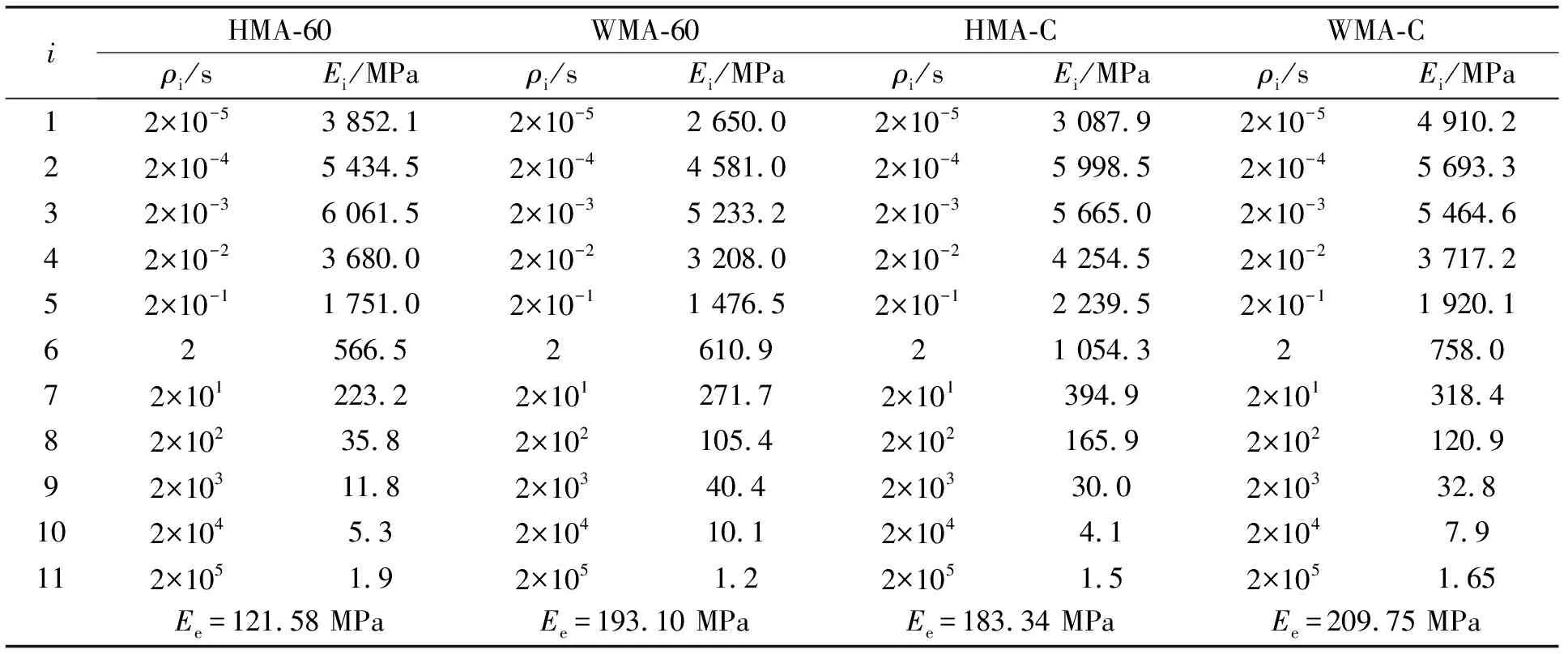
表4 胶粉改性沥青混合料的离散松弛谱

(16)
其中:ef1是误差函数;N是测量的数据点的个数,其值等于28;|E′|m,i是由动态模量和相位角余弦的乘积所得的储量模量的第i个数据点,MPa;|E′|p,i是由Prony级数预测的储量模量的第i个数据点,MPa;|E″|m,i是由动态模量和相位角正弦的乘积所得的的损失模量的第i个数据点,MPa;|E″|p,i是由Prony级数预测的损失模量的第i个数据点,MPa。
一旦确定了公式14和15中的待定系数,那么可用公式17来确定时域下的松弛模量E(t),松弛模量随时间的关系曲线可用图8来表示。

图8 胶粉改性沥青混合料的松弛模量及蠕变柔量主曲线
(17)
其中:E(t)是松弛模量,MPa。
由图8可知,HMA-C的松弛模量总是大于HMA-60的松弛模量;添加温拌剂后,混合料的松弛模量在低时域(低温)范围内下降,而在高时域(高温)范围内增加;WMA-C的松弛模量总是大于WMA-60的松弛模量。这样的结果表明HMA-60的低温松弛能力始终优于HMA-C,也就是说HMA-60较HMA-C具有更好的低温抗裂性能;一旦加入温拌剂,可提高胶粉改性沥青混合料的低温松弛能力,从而提高低温抗裂性能;WMA-60的松弛能力始终优于WMA-C,同样反映出WMA-60较WMA-C具有更好的低温抗裂性能。
3.6.2 胶粉改性沥青混合料的蠕变特性
一旦由动态模量的试验结果按照公式12、13得到了相应的存储模量和损失模量,那么按照公式18的方法可由存储模量和损失模量的结果进一步得到存储柔量和损失柔量的结果。最终将所得的存储柔量和损失柔量用Prony级数的形式表达。其Prony级数的形式分别为公式19和20。
(18)
(19)
(20)
其中:Dg是平衡柔量,MPa-1;η0是零剪切或长时间黏度(对沥青混合料η0→∞),cP;Dj是延迟强度,MPa-1;τj是延迟时间,s;它可由松弛时间的结果并按照Park[44]提出的方法来计算,详细计算过程可以参考Zhang[45]的研究成果,并将最终结果列于表5;w是缩减角频率,其大小等于2πfr。
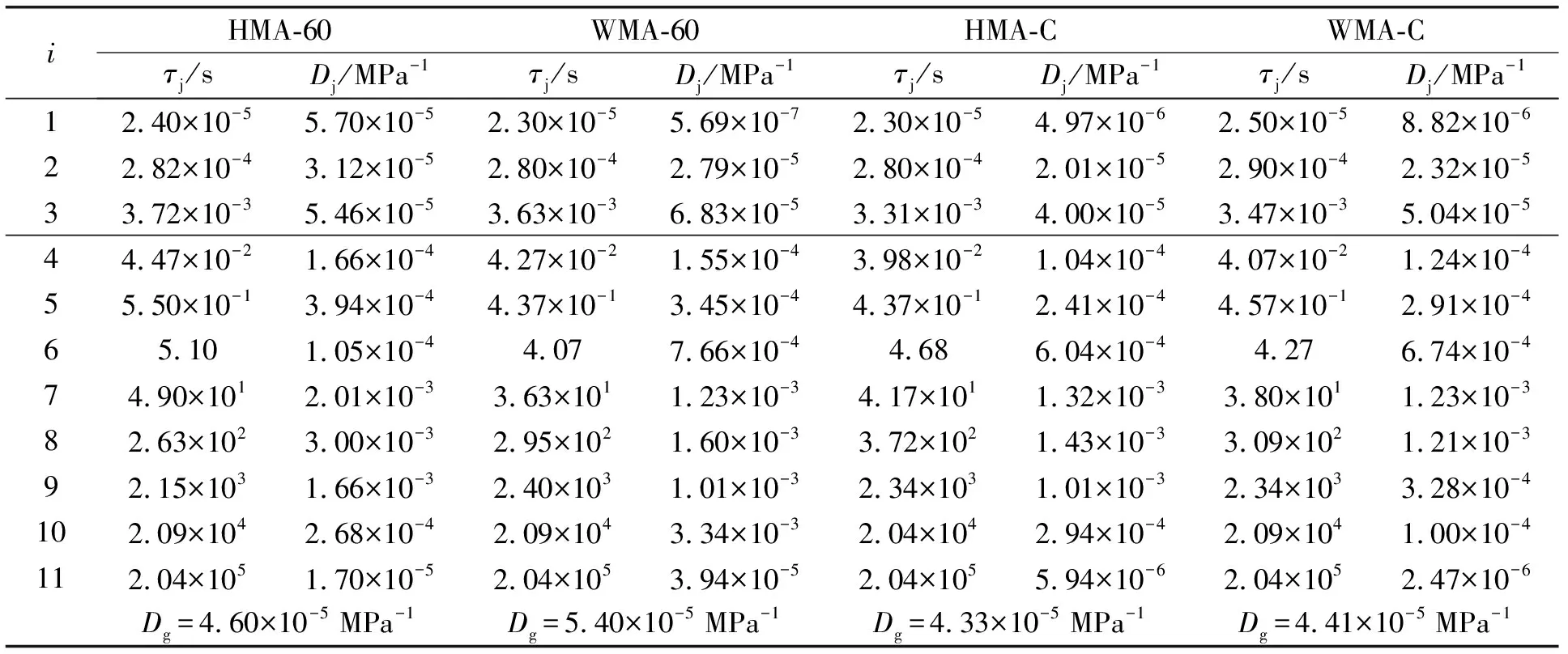
表5 胶粉改性沥青混合料的离散延迟谱
类似于公式14和15的计算过程,这里也可以建立误差函数ef2来同时求解公式19和20中的Prony级数。

(21)
其中:ef2是误差函数;N是测得的数据点的个数,其大小等于28;|D′|m,i是通过储存模量和损失模量得的存储柔量的第i个数据点,MPa-1;|D′|p,i是由Prony级数预测的储存柔量的第i个数据点,MPa-1;|D″|m,i是通过储存模量和损失模量得的损失柔量的第i个数据点,MPa-1;|D″|p,i是由Prony级数预测的损失柔量的第i个数据点,MPa-1。
综上可知,一旦确定了公式19和20中的待定系数,那么按照公式22即可确定时域下的蠕变柔量D(t),蠕变柔量表示单位应力作用下随时间的应变响应,它可作为沥青混合料高温性能的重要评价指标[46]。蠕变柔量随时间的变化如图8所示。
(22)
其中:D(t)是蠕变模量,MPa-1。
如图8同样可知,HMA-C的蠕变柔量小于HMA-60的蠕变柔量;添加温拌剂后,混合料的蠕变柔量在低时域(低温)增加,在高时域(高温)减小;WMA-C的蠕变柔量小于WMA-60。这表明HMA-C的变形能力不如HMA-60;一旦加入温拌剂,可提高胶粉改性沥青混合料的高温抗车辙性能和低温抗裂性;WMA-C的抗车辙性能最优,WMA-60的低温抗裂性最优。这同样是由于同等条件下混合目胶粉改性沥青的粘度大产生的混合料粘聚力也大。混合料在压实过程也需要提供更大的压实功,导致混合目胶粉改性沥青混合料具有较大的强度和抗变形能力;温拌后降低了混合料的拌和温度,在一定程度上减小了沥青老化,沥青的流淌性也变好,更多的沥青可以被集料吸收从而提高结构沥青含量而减少自由沥青含量,最终表现为温拌后混合料的高温抗车辙性能和低温抗裂性均有所提高。
4 结 论
从线性粘弹性出发,采用广义Sigmoidal模型研究了温拌前后胶粉改性沥青混合料的动态模量主曲线,并基于近似K-K关系由斜率法构建了相应的相位角主曲线,根据粘弹参数之前的函数关系进一步得到了松弛模量主曲线和蠕变柔量主曲线用以研究混合料的松弛和蠕变特性,从而评价胶粉改性沥青混合料的高低温性能。主要结论如下:
(1)与动态模量的实测结果相比,根据WLF移位技术构建的广义Sigmoidal动态模量主曲线模型具有非常好的拟合优度,该模型可作为胶粉改性沥青混合料动态模量的预测模型。
(2)与胶粉改性沥青混合料相位角的实测结果相比,由动态模量主曲线斜率法构建的相位角的预测模型也具有较好的拟合优度。
(3)Black Space图和Cole-Cole图都验证了复数模量试验中胶粉改性沥青混合料实测结果的可靠性,此外也证明了广义Sigmoidal动态模量主曲线及其由斜率法构造的相位角主曲线符合线性粘弹性理论。
(4)根据粘弹性理论,由胶粉改性沥青混合料的动态模量主曲线和相位角主曲线可以进一步转化得到时域下高精度的松弛模量主曲线和蠕变模量主曲线。这可避免由蠕变柔量直接转化松弛模量过程中求解卷积分的难题。
(5)HMA-60的高温抗车辙能力不及HMA-C,但低温抗裂性能优于HMA-C。一旦加入温拌添加剂,混合料在高温下的抗车辙能力将得到改善,同时在低温下的抗裂性能也将得到改善。WMA-60的高温抗车辙能力不及WMA-C,但低温抗裂性能优于WMA-C。因此在寒冷地区推荐采用WMA-60,而在炎热地区推荐采用WMA-C。
