嵌岩桩单桩竖向承载力计算方法研究

周 洁，任君杰，李泽垚，刘 钟

(1.同济大学土木工程学院，上海 200092；2.同济大学岩土及地下工程教育部重点实验室，上海 200092;3.中国建筑第二工程局有限公司，北京 100074;4.浙江坤德创新岩土工程有限公司，宁波 315103)

嵌岩桩具有单桩承载力高、群桩效应小、建筑物沉降收敛快等优点，已成为大型桥梁、高层建筑、重型厂房等建筑物的主要基础型式[1-2]。目前获得其单桩承载力的方式有最为基本可靠的静载荷试验和室内模型试验的直接方法[3-5]，也有依靠理论计算和经验数据的间接方法[6-10]和数值模拟法[11-13]，均有学者进行相关研究。然而，由于嵌岩桩具有承载力大、试验耗费高且很难进行破坏性试验等特点，所以快速便捷的嵌岩桩单桩承载力的间接获得方法(规范法、理论法、经验公式法)在工程实践中受到青睐。因此，针对不同间接方法的准确性及其适用性得到了很多研究学者的关注。

陶燕春[14]、史艳等[15]对部分行业标准中关于嵌岩桩单桩竖向承载力计算方法，分别进行探讨并针对其存在的问题提出了相关建议。邢皓枫等[16]对有关嵌岩桩承载力的五种规范所依据的荷载传递机理做了详细论述。吕世明等[17]对比分析规范计算方法和理论计算的优缺点，给出在工程实践中适用嵌岩桩单桩承载力计算方法的建议。许俊等[18]也从多角度考虑《建筑地基基础设计规范》(GB 50007—2011)和《建筑桩基技术规范》(JGJ 94—2008)的适用范围。胡中波等[19]就中外多组嵌岩桩极限侧阻力和极限端阻力静载试验资料,验证已提出的极限侧阻力和极限端阻力经验公式的适用性和有效性。王田龙等[20]通过收集到的嵌岩桩静载试验数据，对侧阻力系数、端阻力系数进行统计分析并其对影响因素进行探讨。张琦等[21]比较了基于岩体二维Hoek-Brown准则的桩端整体滑裂破坏方式下的桩端阻力计算方法及桩周岩体剪切破坏方式下的桩端阻力计算方法、三维Hoek-Brown准则的桩周岩体剪切破坏方式下的桩端阻力计算方法和Ⅰ-Ⅱ型复合判据的桩周岩体微裂纹裂解方式下的桩端阻力计算方法等6种计算方法的实际适用情况。刘海军等[22]基于重庆某典型嵌岩桩工程实例数据，对现行规范计算方法进行比较，分析各计算方法结果差异和工程实践中的适用性。王鹏程等[23]通过比较贵州软质较破碎白云岩嵌岩桩竖向承载力的实测值和规范计算值，发现实测承载力比计算值高出数倍。谢一凡等[24]在规范计算方法的基础上，提出了桩身穿过一层或多层强风化软弱夹层的承载力计算经验计算方法。Dai等[25]总结了嵌岩段桩侧阻力及端阻力设计计算常用的经验公式，并定性分析了粗糙度、清孔程度、长径比、内摩擦角等因素对单桩竖向承载力的影响。Mohammad等[26]就迪拜地区的嵌岩桩嵌岩段桩侧阻力数据分析比较不同嵌岩段桩侧阻力经验公式的适用性。Arioglu等[27]将其提出的嵌岩段桩侧阻力经验公式所采用的数据集与Rezazadeh等[28]在2017年提出的嵌岩段桩侧阻力经验公式所采用的数据集合并，重新进行回归性分析，并对其原有的嵌岩段桩侧阻力经验公式进行讨论和修正。Serrano等[7]采用Lambe变量和瞬时摩擦角，实现了Hoek-Brown准则和Mohr-Coulomb之间的转换，通过无量纲转换得到了更为简便的嵌岩段桩侧阻力的计算公式，并将其计算结果和平面应变数值模拟的结果进行比较。对于桩端阻力的计算，Serrano等[29-30]也在结合Meyerhof地基极限承载力公式及滑移线场方法的基础上，提出了形式简单的桩端阻力计算公式。

但上述大部分的中外学者都仅以规范计算法、理论计算法及经验公式计算法中的一种或两种方法为研究对象，很少有学者将规范法、理论法和经验公式法就多组相同数据进行系统的横向比较，分析其适用范围、预测准确性及实际工程实践中的优选方法。为此，将分别对规范法、理论法及经验公式法进行论述，并采用多组工程实际数据对各个方法的估算准确性进行比较，针对不同方法在预测过程中表现出的优缺点提出一些在工程实践中所涉及的嵌岩桩单桩承载力问题的计算方法适用建议。

1 嵌岩桩单桩竖向承载力计算方法

1.1 规范法

随着经济和技术的不断发展，目前工程项目所面临的工况也逐渐复合化。同一个工程参数往往有多部规范及标准进行不同的规定，因此规范的选用就成为了工程实践中常常出现的问题。在嵌岩桩单桩承载力的估算中同样面临上述的问题，现行有关嵌岩桩的行业规范主要有：《港口工程嵌岩桩的设计与施工规程》(JTJ 285—2000)[31]、《建筑地基基础设计规范》(GB 50007—2011)[32]、《建筑桩基技术规范》(JGJ 94—2008)[33]、《铁路桥涵地基和基础设计规范》(TB 10093—2017)[34]、《公路桥涵地基与基础设计规范》(JTG 3363—2019)[35]，其中有关嵌岩桩的计算公式如表1所示。

由表1可以得出如下结论。

表1 各规范嵌岩桩单桩竖向承载力计算公式[31-35]Table 1 Calculation formula of vertical bearing capacity of rock stocked pile in various standards[31-35]

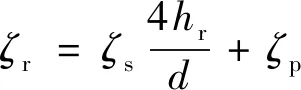
(2)规范中嵌岩段桩端阻力和侧阻力都是以岩石饱和单轴抗压强度乘以对应系数作为计算值，但不同规范中各系数的取值范围和不同的影响因素有关，如表2所示。

表2 各规范计算系数的影响因素Table 2 Influencing factors of the coefficients in various standards

由表2可知，不同规范中的嵌岩段端阻力和侧阻力的计算系数都考虑到岩石破碎(风化)程度的影响；其中《港口工程嵌岩桩的设计与施工规程》(JTJ 285—2000)[31]和《建筑桩基技术规范》(JGJ 94—2008)[33]均涉及嵌岩深径比hr/d的影响；而《铁路桥涵地基和基础设计规范》(TB 10093—2017)[34]、《公路桥涵地基与基础设计规范》(JTG 3363—2019)[35]及《建筑桩基技术规范》(JGJ 94—2008)[33]都考虑到了成桩工艺及清底情况对嵌岩段桩端阻力和侧阻力的影响。但在这5个现行规范中，《建筑桩基技术规范》(JGJ 94—2008)[33]考虑到的影响因素是最为全面的。

1.2 理论法

理论计算公式大多都需要结合荷载传递法，而该种方法需要通过实测得到桩侧、桩端荷载位移关系或者其他参数，且还需将构建的荷载传递函数代进控制微分方程求得桩端阻力或桩侧阻力。计算过程相较于经验公式计算方法和规范法计算方法，较为烦琐，而旨在比较能快速便捷估算嵌岩桩单桩承载力的方法，所以仅对不需要结合荷载传递法的理论计算法进行讨论。

1.2.1 嵌岩段侧阻力

基于对大量岩石体抛物线型破坏包络线的系统研究，Hoek等[36]提出了既满足结构完整的各向同性均质岩石，又适用于碎裂岩体及各向异性非均质岩体的岩石破坏经验判据，并对该准则进行了修正[37]，该方法的基本表达式为

(1)

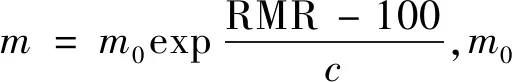
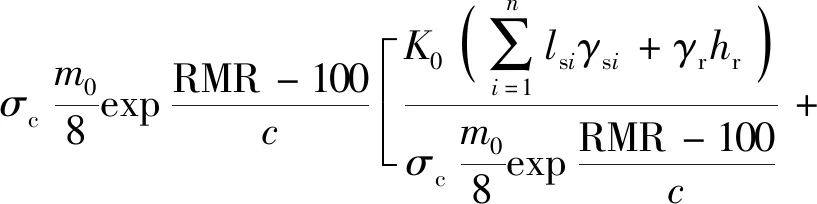
(2)

(3)

式中：f=ce/(c-2e)；hr为嵌岩深度；lsi、γsi分别为第i层土的厚度和重度；γr为岩石的重度；Qr为嵌岩段侧阻力。

Jonhston等[41]研究表明，结构面剪切过程通常包含滑动剪胀和剪切滑移两种机理。邢皓枫等[10]考虑到嵌岩桩浇注过程伴随而来的胶结作用，将完整的嵌岩桩桩-岩界面的剪切过程分为胶结破坏、滑动剪胀及剪切滑移3个阶段，并采用3段线性函数来描述桩-岩界面的剪应力-剪切位移关系。最终根据荷载传递理论，分别得出桩体在剪切区、剪胀区及胶结区下对应的侧阻力。董平等[42]也将结构面剪胀破坏机制和荷载传递法相结合，建立了适用于弱质岩石嵌岩段的端阻力和嵌岩段侧阻力的解析解。而叶观宝等[8]、戴国亮等[9]考虑到桩-岩界面的剪胀效应，对Serrano等[29-30]基于Hoek-Brown准则提出的算法进行修正，如式(4)～式(7)所示：

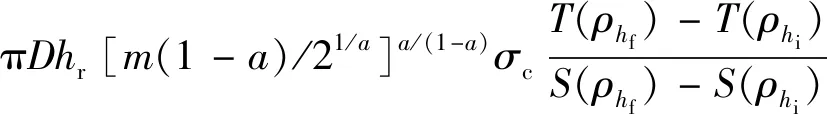
(4)

(5)

(6)

(7)

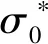
1.2.2 嵌岩段端阻力

Serrano等[29-30]基于Hoek-Brown 岩体经验强度准则，应用Meyerhof地基极限承载力公式求解深基础极限承载力模型及滑移线场方法，推导出具有广泛适用性的简单嵌岩桩桩端极限承载力计算公式为

(8)

式(8)中：Nσ为承载力系数；NβP为嵌岩深径比hr/d和岩体无侧限抗压强度σc的函数;qb为桩端阻力。

Kulhawy等[43]提出了基于二维Hoek-Brown准则，并考虑了桩端面以上岩土层自重影响的嵌岩桩桩端整体滑裂破坏下的极限承载力，计算公式为

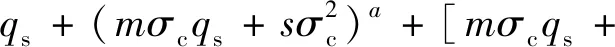
(9)

式(9)中：qs为上覆土层自重。

Zhang等[44-45]又将其扩展至真三维，考虑中主应力σ2影响。Zhang等[46]、崔科宇等[47]考虑到目前广泛适用的Hoek-Brown(H-B)，Mohr-Coulomb(M-B)准则往往忽略了中主应力的影响，在假定桩端岩体破坏服从广义非线性统一强度准则的基础上,利用滑移线场方法,推导嵌岩桩桩端极限承载力。最终的桩端极限承载力公式为

qb=Nβσc

(10)

式(10)中：Nβ由滑移线场方法中的边界条件通过一系列复杂的计算求得。

李镜培等[48]利用滑移线理论并通过叠加的方法分析出桩端基岩破坏时的最危险点，并根据Mindlin 课题求出该点的应力,运用Griffith 准则的Murrell 推广导出桩端极限承载力的公式为

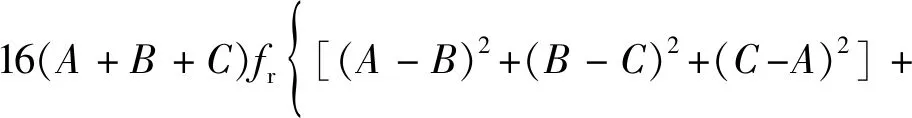
(11)

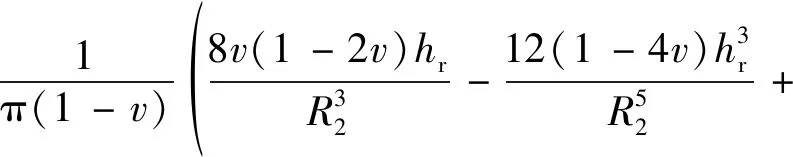
(12)

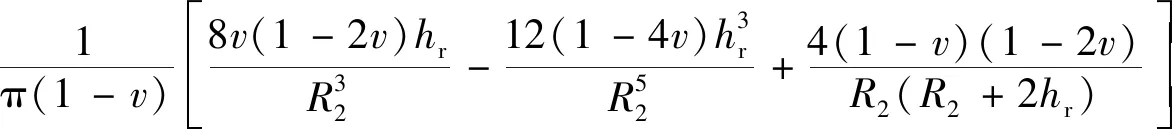
(13)

(14)

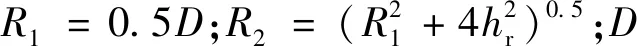
赵明华等[6]根据极限平衡原理，推导了在剪切破坏模式下的嵌岩桩桩端极限承载力的计算公式为

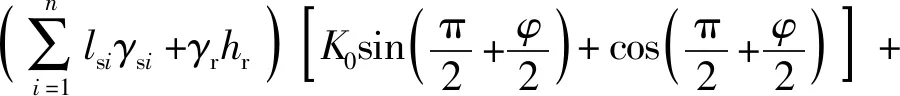
(15)

范秋雁等[49]对刚塑性太沙基理论计算承载力公式进行修正，提出了针对泥岩桩端承载力的计算公式为

qb=2.142cNc+0.255γlL0.7Nq+1.130γdNγ

(16)

式(16)中：Nc、Nq、Nγ为相应项的太沙基承载力系数，Nc=(Nq-1)cotφ，Nγ=1.8(Nq-1)tanφ，Nq=eπtanφtan2(45°+φ/2)，其中φ为地基土的内摩擦角。

1.3 经验公式法

经验估算法是基于实测数据建立嵌岩桩极限侧阻力和极限端阻力与岩体强度的经验关系,以预测同类工程嵌岩桩的竖向承载能力。该方法形式简单、计算简便、可综合考虑岩体类型、结构面特征、桩岩界面粗糙度等的影响。

1.3.1 嵌岩段侧阻力

多位学者经过实验数据的系统分析，认为嵌岩桩的嵌岩段极限侧阻力标准值与岩体无侧限抗压强度存在的经验关系可表示为

qs=α(σc)β

(17)

式(17)中：qs为嵌岩桩的极限侧阻力标准值，MPa；σc为岩体无侧限抗压强度，MPa；α、β为经验系数，其中α为折减系数，与桩岩面接触粗糙度、岩石黏聚力与摩擦强度、岩石风化程度、岩体连续性等因素相关，由中外学者提出的经验公式如表3[19,26-28,43,50-57]所示。

将表3中经验公式在qs-σc坐标轴上表示出来，可知各经验公式计算值的大致趋势，如图1所示，除Reynolds(1980)及Toh(1989)提出的是线性公式，其余指数型公式增长都较为平缓。且只有Arioglu(2007)和计算值最大为Reynolds(1980)和胡中波(2018)针对经验公式提出了不同岩性的适用要求，且胡中波(2018)对于5种不同岩性都分别提出了经验公式，其覆盖范围较大，在适用时可按照不同岩性针对性地选择经验公式。

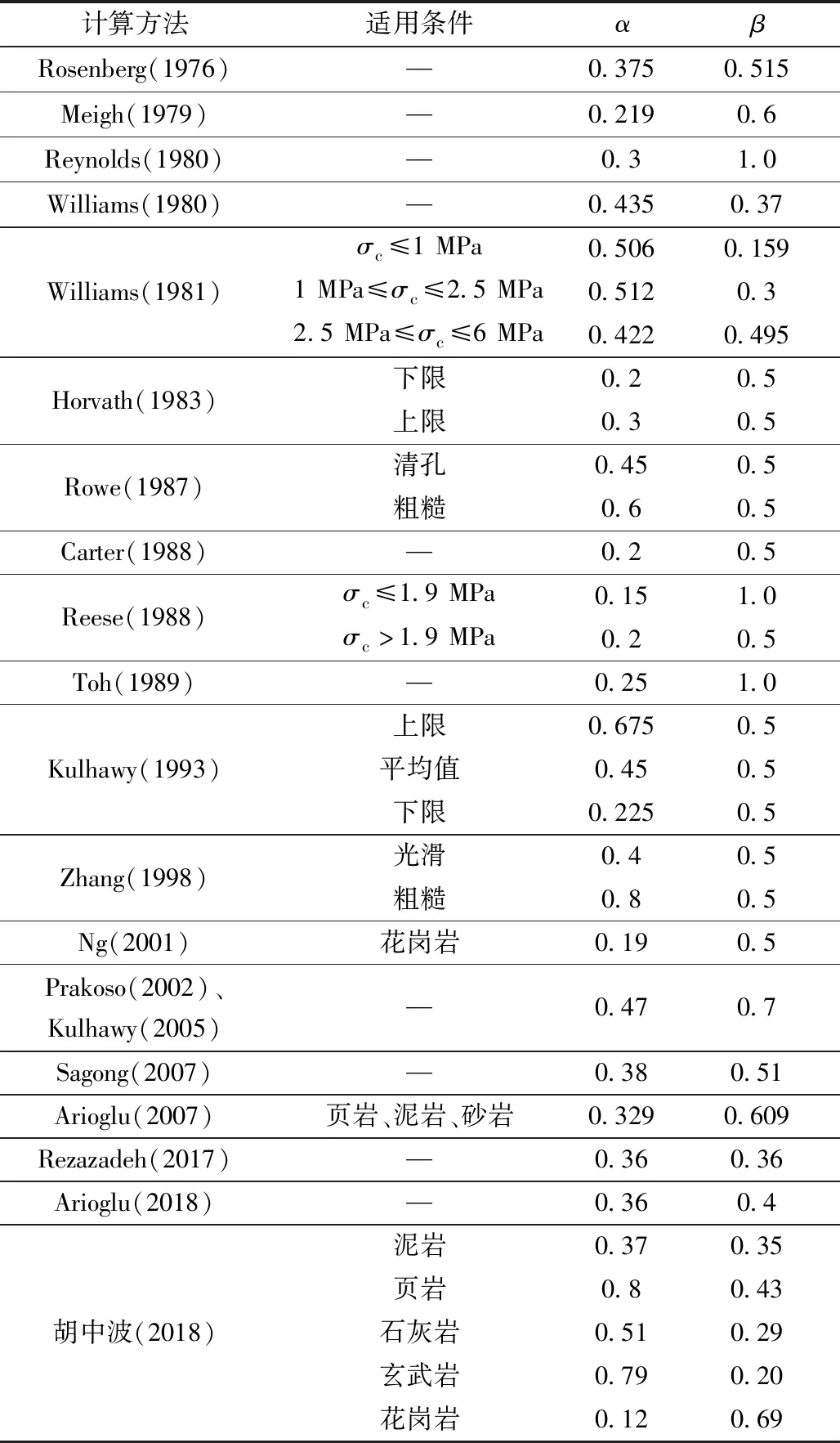
表3 嵌岩桩单桩极限侧阻力经验公式α、β值[19,26-28,43,50-57]Table 3 Values of α and β value in empirical formulas for side resistance of rock stocked pile[19,26-28,43,50-57]

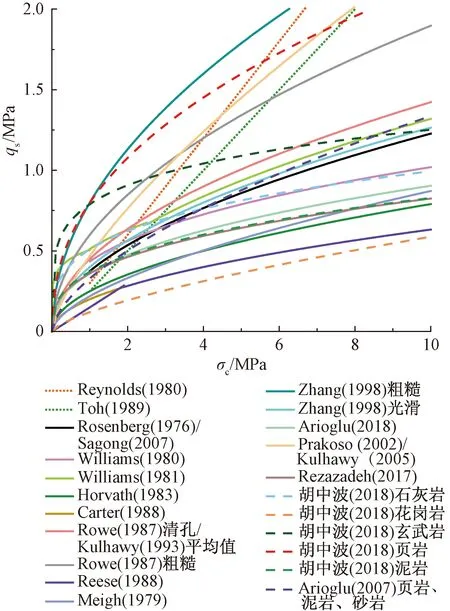
图1 qs-σc坐标上的嵌岩桩单桩嵌岩段极限侧阻力经验公式Fig.1 Empirical formulas for side resistance of rock stocked pile on qs-σc coordinate

1.3.2 嵌岩段端阻力

嵌岩桩侧阻与端阻的发挥是异步的，即侧阻先于端阻发挥[16]。同上，许多学者也基于试验实测数据建立了极限端阻力标准值与岩体无侧限抗压强度的经验关系可表示为

qb=m(σc)n

(18)

式(18)中：qb为嵌岩桩的极限端阻力标准值,MPa；σc为岩体无侧限抗压强度，MPa；m、n为经验系数，中外学者所提出的经验公式由表4[19,43,53,58-61]所示。

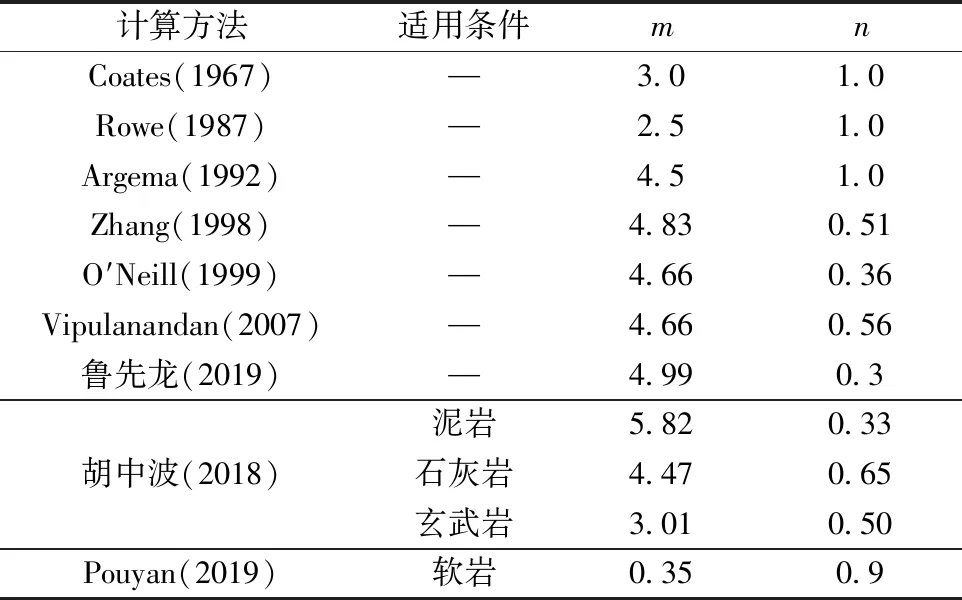
表4 嵌岩桩单桩极限端阻力经验公式m、n值[19,43,53,58-61]Table 4 Values of m and n in empirical formulas for end resistance of rock stocked pile[19,43,53,58-61]

图2为上述经验公式在qb-σc坐标轴上的表示。除部分线性公式外，其余指数型公式都较为平缓且趋势较为一致。计算值最大为Argema(1992)计算公式，计算值最小为胡中波(2018)适用于玄武岩的经验公式，且因为胡中波按照不同岩性提出了不同的经验公式，其覆盖范围较大，可大致囊括其他学者提出的经验公式。

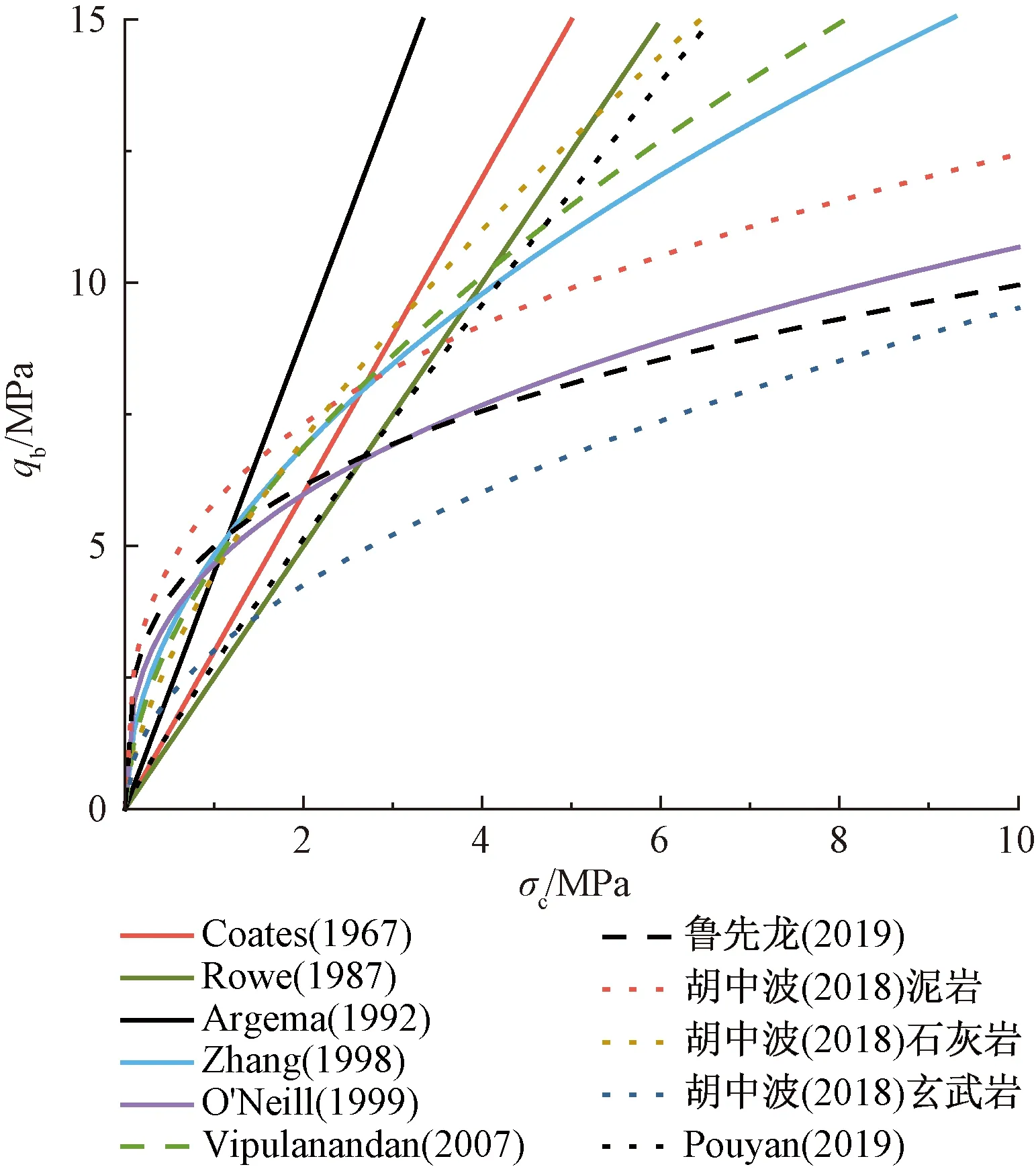
图2 qb-σc坐标上的嵌岩桩单桩极限端阻力经验公式Fig.2 Empirical formulas forend resistance of rock stocked pile on qb-σc coordinate

2 工程实例验算及结果分析

2.1 工程实例1

2.1.1 工程概况及计算数据

文献[62]采用自平衡测试方法对南京长江第三大桥桥基3根工程试桩进行了基桩承载性能的试验研究。由于其中3号桩地质资料较完整，选取3号桩进行计算分析。3号桩为嵌岩桩，桩径d为1.5 m；有效桩长L为43 m；上部土层约25 m，取其加权平均重度γs为18.5 kN/m3；下部嵌入岩层约18 m，取其加权平均重度γr为25 kN/m3；嵌岩比hr/d为12。桩端持力层为微风化泥岩，参考Hoek-Brown提出的较为全面的m0取值[63-65]，本实例中取m0为10。计算所需各层岩土试验参数和总承载力及嵌岩段桩侧、桩端承载力如表5[6]和表6[6]所示。桩顶荷载-桩顶位移曲线如图3[59]所示，按照《建筑桩基检测技术规范》(JGJ 106—2014)，对于陡降型Q-s曲线，取其发生明显陡降的起始点对应的荷载值为单桩极限承载力。

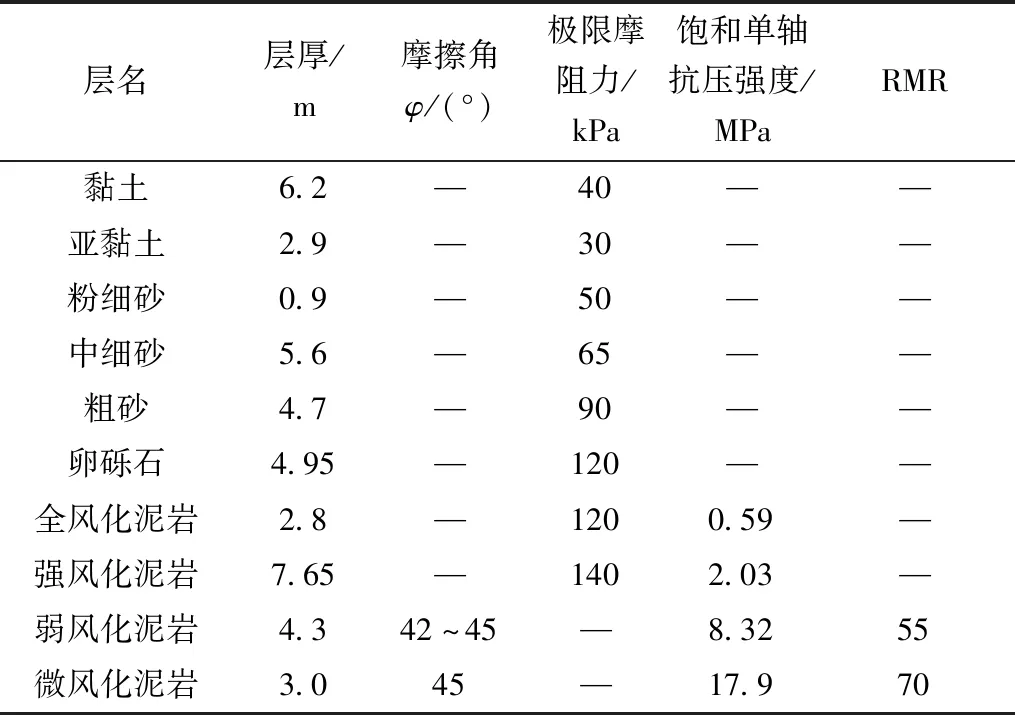
表5 实例1各岩层土试验参数[6]Table 5 Parameters of value of each stratum in the first project[6]

表6 实例1实测值[6]Table 6 Measured values of the first project[6]

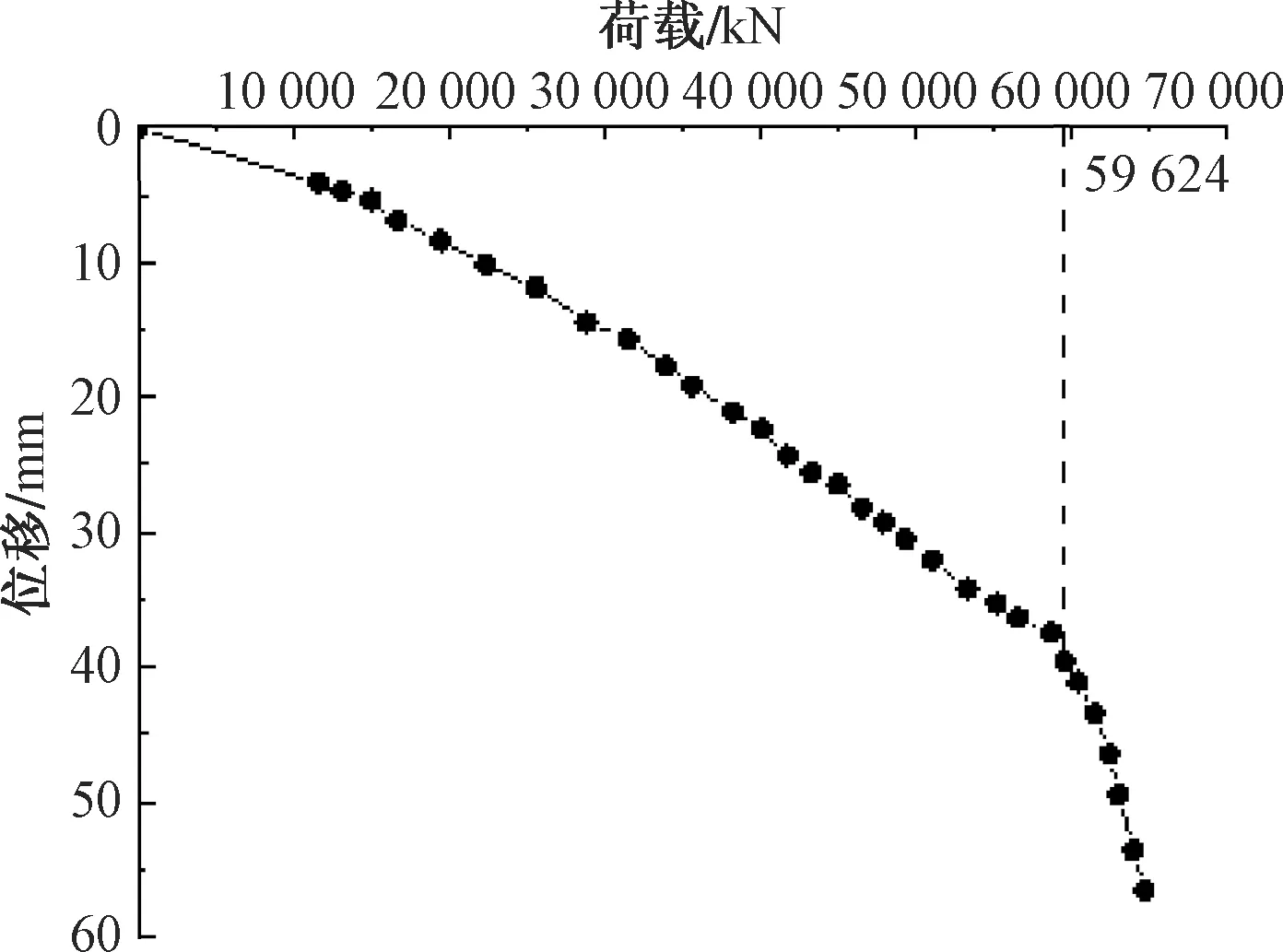
图3 实例1桩顶荷载-桩顶位移Q-s曲线[59]Fig.3 Load-displacement Q-s curve of the first project[59]

2.1.2 规范法、理论法及经验公式法验证结果

(1)规范法验证结果。根据获取数据按照1.1节中所述不同规范中的计算公式，结果如表7所示。

由表7可知，按照5种不同规范中对嵌岩桩极限承载力规定的计算方法计算实例1，除《公路桥涵地基与基础设计规范》(JTG 3363—2019)[35]外，其余4种规范计算得到的总极限承载力均小于实测值，偏于安全。且在其中《建筑桩基技术规范》(JGJ 94—2008)[33]和实际值最为接近。

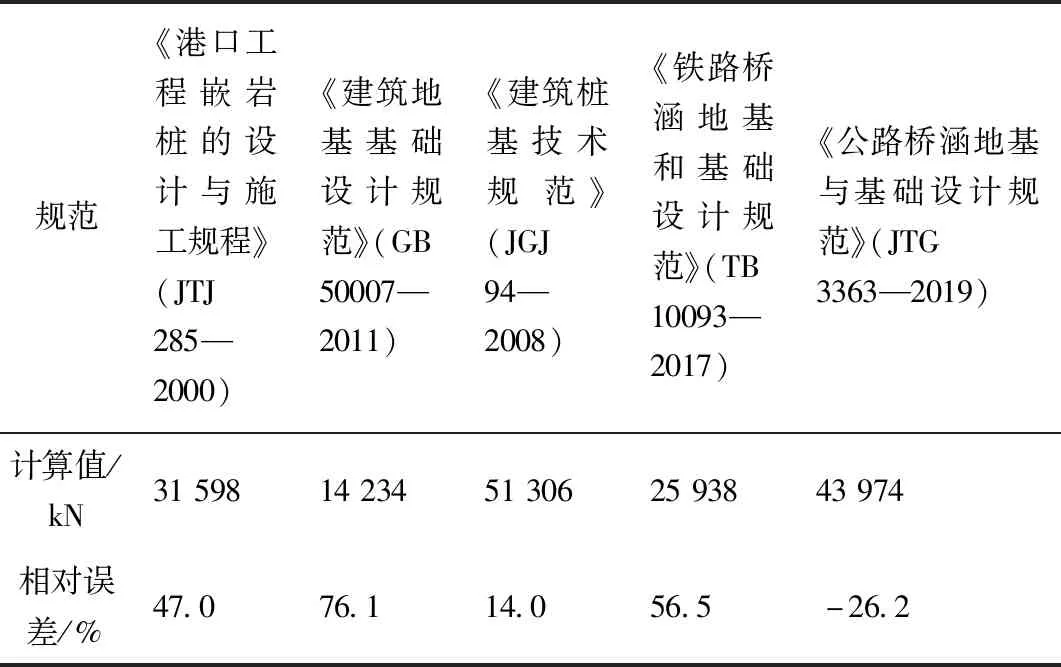
表7 规范法实例1计算结果Table 7 Results of standard method applied in the first project

(2)理论法验证结果。研究目的在于比较能快速便捷估算嵌岩桩单桩承载力的方法，因此相较于仅需要知道饱和单轴抗压强度或岩体无侧限抗压强度的规范计算法和经验公式计算法，文献[6]基于Hoek-Brown强度准则提出的嵌岩桩桩端及嵌岩段桩侧的极限承载力计算方法和文献[48]提出桩端极限承载力的计算方法，这上述的两种理论计算法计算过程较为简单，且所需参数较少，故选择上述两种方法作为理论计算方法的工程实例验算方法，结果如表8所示。

由表8可知，两种理论计算法计算得到的结果均和实际值较为接近，但文献[6]计算得到的嵌岩桩极限承载力和总桩侧阻力均比实测值稍大。文献[48]提出的计算方法得到的桩端阻力比文献[6]采用极限平衡原理得到的桩端阻力更接近实测值，因其物理意义更加明确。即按照理论计算法计算得到的结果来进行嵌岩桩承载力的设计，不会过于保守，能够节约工程成本。

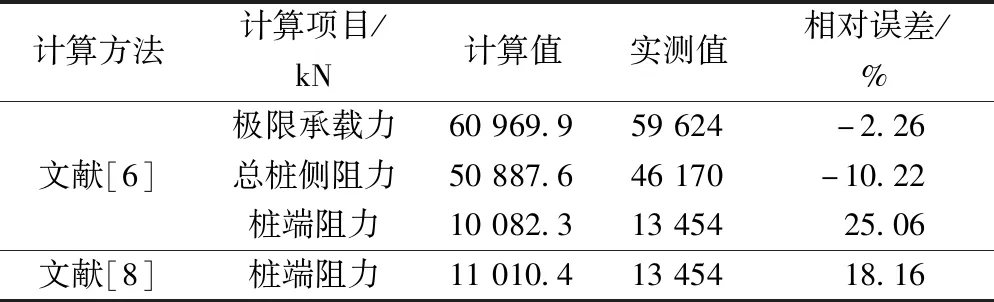
表8 理论法实例1计算结果[6,48]Table 8 Results of theoretical methods applied in the first project[6,48]

(3)经验公式法验证结果。在此实例中，根据数据对1.3节中的嵌岩段桩侧阻力经验公式和桩端阻力经验公式进行验算，结果如表9所示。

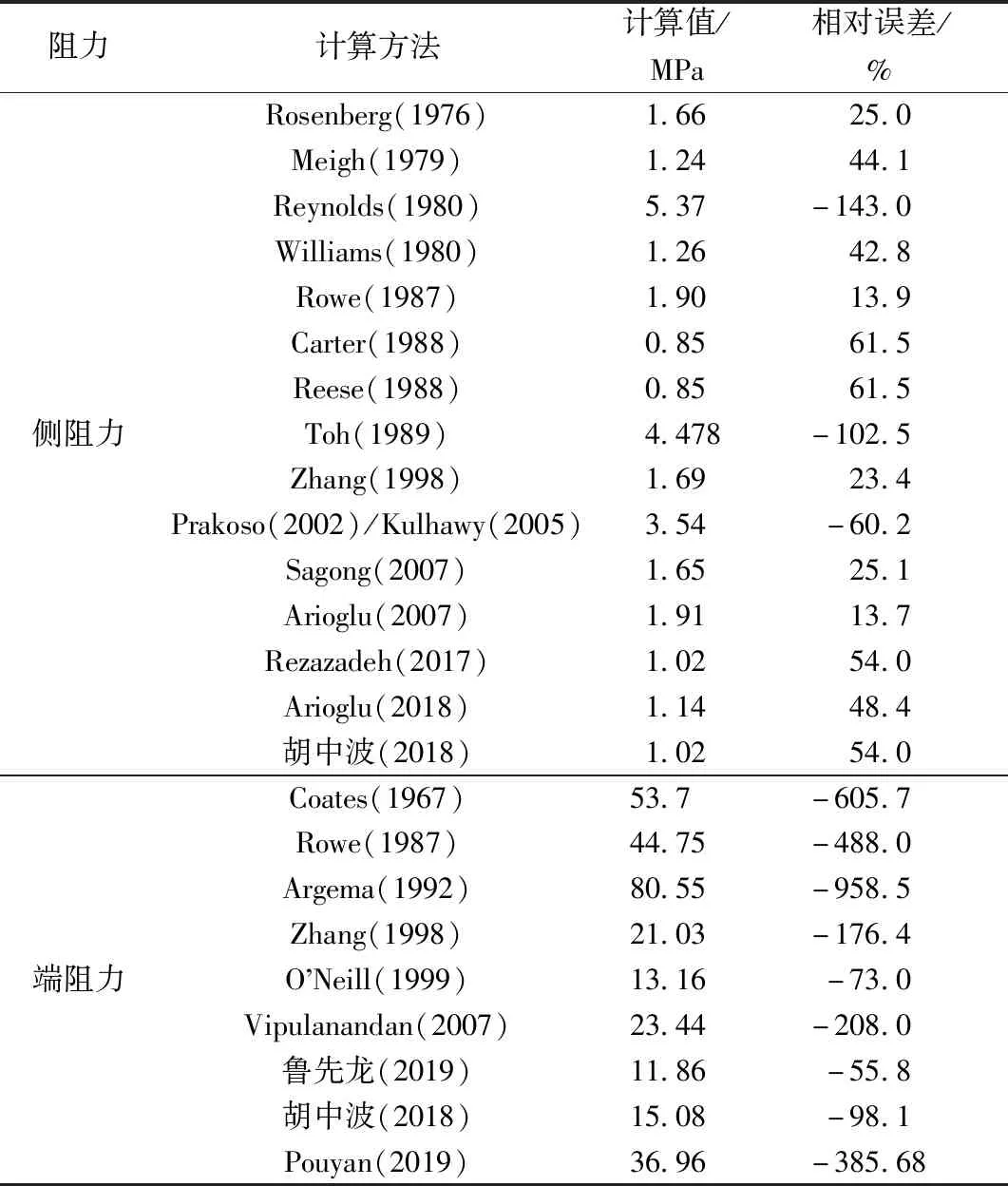
表9 嵌岩段桩侧阻力及端阻力经验公式法实例1计算结果[19,26-28,43,50-61]Table 9 Results of theoretical methods applied in calculating side resistance and end resistance of rock stocked pile in the first project[19,26-28,43,50-61]

从表9可知，Reynolds(1980)及Toh(1989)提出的两个线性经验公式，其计算结果均大于实测值，按该值进行嵌岩桩的单桩承载力设计较为危险。而在非线性公式中，除Prakoso(2002)和 Kulhawy(2005)提出的经验公式计算结果偏大，其余的经验公式计算结果都小于实测值，较为安全，其中Arioglu(2007)提出的经验公式最接近实测值。表10的桩端经验公式验算结果表明，在该实例的验算中，桩端阻力的经验公式计算结果均大于实测值，且和实测值相差较大，故而在该实例中，不适合适用经验公式计算法估算桩端阻力。若按该计算方法求得的桩端阻力进行嵌岩桩承载力性能的设计，将会偏于危险。

2.2 工程实例2

2.2.1 工程概况及计算数据

文献[66]采用自平衡测试方法对东莞东江大桥两根非工程桩进行了静载试验研究。该大桥采用钻孔灌注桩基础，且几乎全部嵌固在岩石中。选取其中S6AT号试桩进行研究。S6AT号试桩桩径d为1.5 m；有效桩长L为23 m；上部土层约1.3 m，取其加权平均重度γs为18 kN/m3；下部嵌入岩层约21.7 m，取其加权平均重度γr为24.5 kN/m3。桩端持力层为微风化泥质粉砂岩，参考文献[60-62]提出的较为全面的m0取值表，本实例中取m0为10。计算所需各层岩土试验参数和总承载力及嵌岩段桩侧、桩端承载力如表10[6]、表11[6]所示。桩顶荷载-桩顶位移曲线如图4[63]所示，按照《建筑桩基检测技术规范》(JGJ 106—2014)，对于陡降型Q-s曲线，取其发生明显陡降的起始点对应的荷载值为单桩极限承载力。

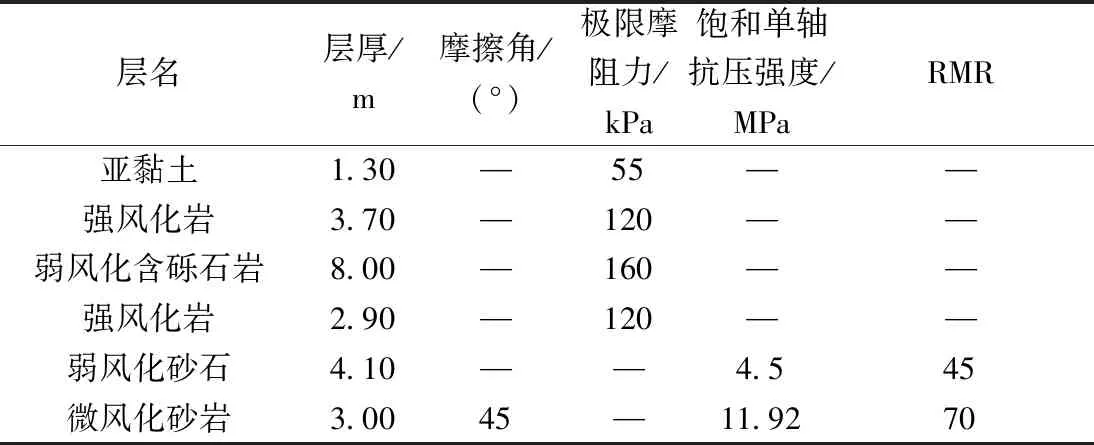
表10 实例2各岩层土试验参数[6]Table 10 The parameters of value of each stratum in the second project[6]

表11 实例2实测值[6]Table 11 Measured values of the second project[6]

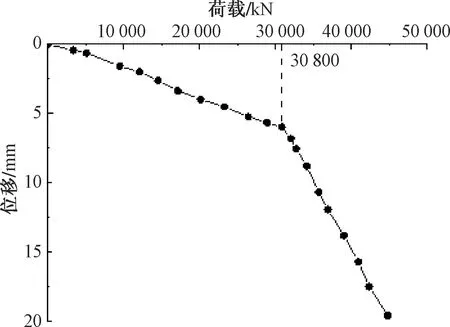
图4 实例2桩顶荷载-桩顶位移Q-s曲线[63]Fig.4 Load-displacement Q-s curve of the second project[63]

2.2.2 规范法、理论法及经验公式法验证结果

(1)规范法验证结果。根据获取数据按照1.1节中所述不同规范中的计算公式，计算结果如表12所示。

由表12可知，用5种现行规范验算实例2得到的计算结果，除《建筑桩基技术规范》(JGJ 94—2008)[33]外，其余均大于实测值，且《建筑桩基技术规范》(JGJ 94—2008)[33]计算得到的总承载力值和实测值最为接近。

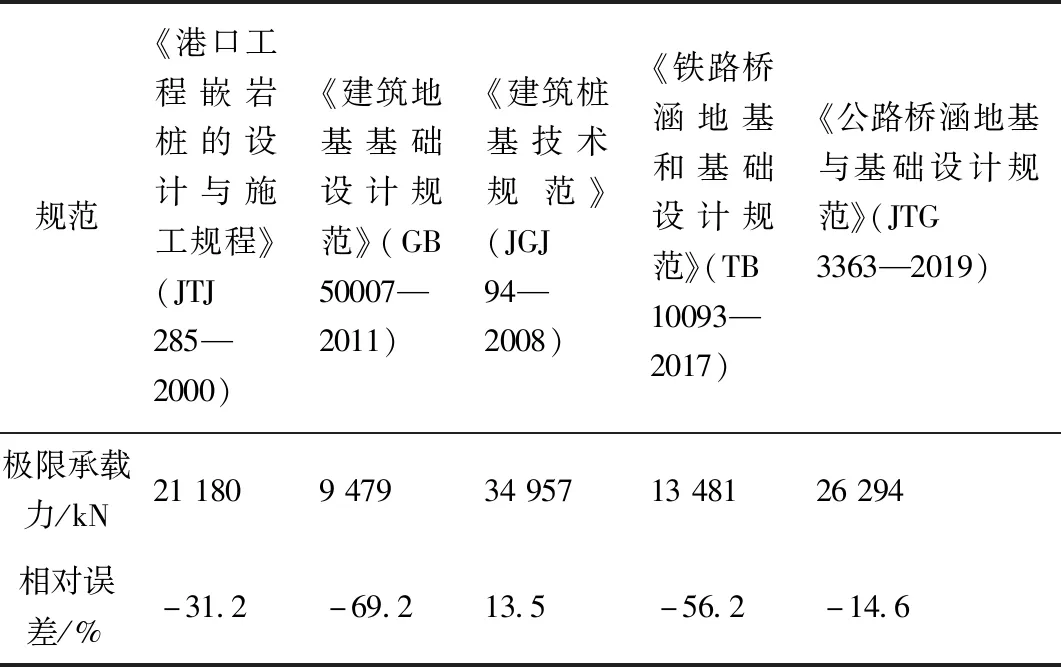
表12 规范法实例2计算结果[31-35]Table 12 Results of standard method applied in the second project[31-35]

(2)理论法验证结果。同上，采用文献[6]基于Hoek-Brown强度准则提出的嵌岩桩桩端及嵌岩段桩侧的极限承载力计算方法和文献[48]提出桩端极限承载力的算方法对嵌岩段侧阻力和桩端阻力进行验算，并和实测值比较，其结果如表13所示。在实例2的验算中，两种理论法的适用结果和其在实例1中的适用结果相同。

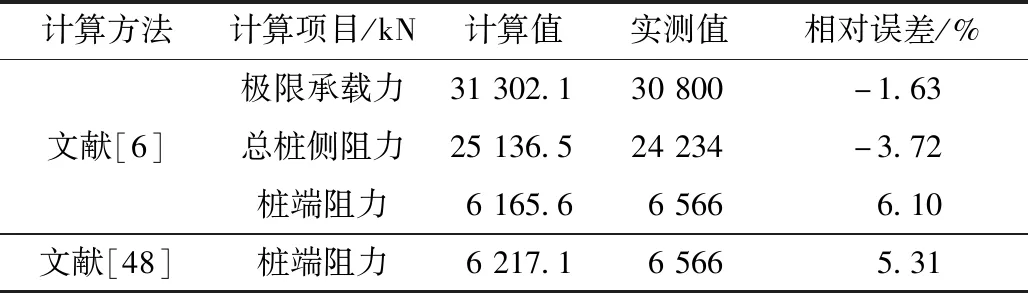
表13 理论法实例2计算结果[6,48]Table 13 Results of theoretical methods applied in the second project[6,48]

(3)经验公式法验证结果。同上，根据实例2中的数据对1.3节中的嵌岩段桩侧阻力经验公式和桩端阻力经验公式进行验算，结果如表14所示。

由表14可知，在实例2中适用嵌岩段桩侧阻力经验公式时，Reynolds(1980)及Toh(1989)提出的两个线性经验公式，其计算结果均大于实测值，按该值进行嵌岩桩的单桩承载力设计较为危险。而在非线性公式中，除Prakoso(2002)、Kulhawy(2005)、Rowe(1987)及Arioglu(2007)提出的经验公式计算结果偏大，其余的经验公式计算结果都小于实测值，较为安全。其中Arioglu(2007)针对页岩、泥岩和砂岩提出的经验公式最接近实测值。且线性经验公式较非线性经验公式偏离实测值更大。而桩端阻力的经验公式计算结果均大于实测值，且和实测值相差较大。

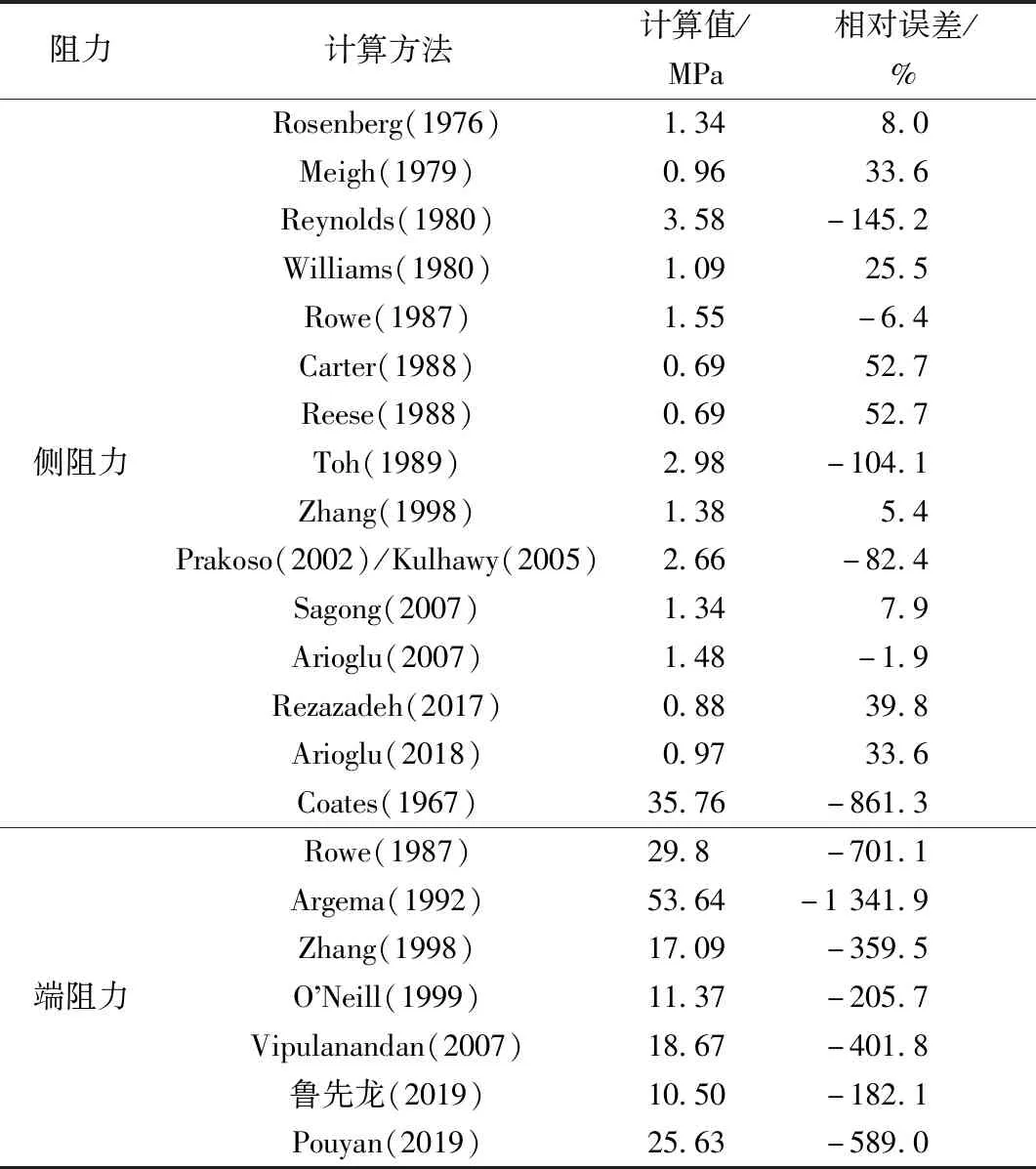
表14 嵌岩段桩侧阻力及端阻力经验公式法实例2计算结果Table14 Results of theoretical methods applied in calculating side resistance and end resistance of rock stocked pile in the second project

2.3 规范法、理论法及经验公式法对比分析讨论

通过整体分析得到的两组结果，可得出如下结论。

(1)在规范计算法的工程实例验算中，只有《建筑桩基技术规范》(JGJ 94—2008)[33]在两个工程实例中均最为接近且小于实测值，从各个规范表达式的荷载传递机理来看，《建筑桩基技术规范》(JGJ 94—2008)[33]公式所表达的物理意义最接近实际，其考虑到的影响因素也最为全面。

(2)在理论计算方法的两项工程实例验算中，文献[6]计算得到的嵌岩桩极限承载力和总桩侧阻力均比实测值稍大，但基于极限平衡原理得到的桩端阻力则小于实测值。而文献[48]基于滑移线场理论运用Griffith 准则的Murrell 推广得到的桩端阻力更接近实测值，且该方法只需要泊松比ν、嵌岩段桩径D、岩石饱和单轴抗压强度标准值frk及嵌岩深度hr4个参数即可，计算过程也不需要积分运算，较文献[6]提出的桩端阻力计算方法更为简便。

(3)在嵌岩段桩侧阻力、端阻力经验公式的验证中，各个嵌岩段桩侧阻力经验公式得到的计算值和实测值的差距相较于桩端经验公式得到的计算值和实测值的差距较小。且在两个工程实例的适用中，各个桩端阻力的经验公式计算值和实测值相差较大，均大于实测值。此外，非线性经验公式计算得到的极限侧阻力标准值与实测值的一致性更佳,且均优于线性公式，其计算结果也会明显大于实测值。

(4)综合比较以上3种嵌岩桩承载力的估算方法在两项工程实例中的适用，最接近实测值的均是理论法，其次是规范法，计算结果最不稳定的是经验公式法。由上可知，不同算法计算结果的准确性高低和其所表达的荷载传递机理与实际嵌岩桩受荷性状的接近程度有关。理论法的计算公式具有明确的物理意义，且其较能体现嵌岩桩实际的受荷性状，故而和实测值较为接近。且理论法对于不同的工况能进行单独的分析计算。而经验公式估算法和规范法均是是基于大量数据的统计值，不能贴近每一个工程实例的实际工况。但就简便性和快速性，经验公式法和规范法相较于理论法还是具有一定的优势。

3 结论与建议

结合两项工程实例数据，对规范法、理论法及经验公式法的应用验算结果进行对比分析，针对嵌岩桩单桩承载力计算的优选方法及误差来源得出如下结论。

(1)当需要对嵌岩桩单桩承载力进行较为准确的估算时，可首选理论法进行预估，此种方法物理意义明确，可以在保证安全的基础上达到节约工程成本的目的。

(2)考虑到当前工程实践常涉及多种工况的复合，当有多部规范可选用时，需综合分析不同规范所体现的荷载传递机理和实际性状的接近程度来选择适用规范。《公路桥涵地基与基础设计规范》(JTG 3363—2019)及《建筑桩基技术规范》(JGJ 94—2008)中的计算公式体现的受荷性状中最为接近实际且考虑影响因素较为全面，可优先选用。而建筑地基基础设计规范》(GB 50007—2011)将嵌岩桩完全当作端承桩处理，最为不合理，除特殊情况有所规定，应尽量避免选择该规范的估算方法进行计算。

(3)经过数据验算分析，经验公式方法只可在条件特别简单，地层情况非常有利的情况下简单采用，或对规范法进行补充验证，非常不适用于实际工程中嵌岩桩嵌岩段桩侧阻力和桩端阻力的估算，因其来源于大量数据的统计值，缺乏具体的物理意义，且部分经验公式没有对适用岩性做出规定，必然会导致在适用经验公式估算嵌岩段桩侧阻力和桩端阻力时存在较大误差。

(4)通过实例验算，3种嵌岩桩承载力估算方法的准确程度和其所表达的嵌岩桩受荷性状和实际受荷性状的接近程度存在较强的关联性，而和需要参数的多少关联性较小，即并不是参数越多，计算结果越接近实际。因此建议在进行嵌岩桩单桩承载力验算的过程中，不能仅以参数的多少来判断该计算方法的优劣，而是需要综合考虑其所表达的受荷机理和实际性状的接近程度及计算过程的复杂程度来选择在当前已知条件下较为适合的计算方法。

为使得研究结果尽量普适性高，选取2个代表性工程实例进行验算，但依然不能避免存在偶然性，在后续研究中，可以结合大数据对嵌岩桩单桩承载力进行对比分析，给出更为准确可行的优化方法。尤其可深入分析嵌岩桩的荷载传递机理，针对理论计算方法烦琐性高、计算过程复杂等问题进行合理性简化，以便在不失计算准确性的同时提高其可操作性。同时也可依靠大数据，有针对性地得到不同岩性对应的嵌岩段桩侧阻力和桩端阻力经验预测公式，以便能在较短时间内得到较为接近实测值的结果，提高经验计算法的准确性。