基于主成分分析的碳酸盐岩裂缝识别方法

曹继飞，邹德永，舒腾飞，王子振

(1.中国石油大学(华东)石油工程学院，青岛 266580；2.中石化胜利石油工程公司钻井工艺研究院，东营 257000)

裂缝是碳酸盐岩油气藏的重要储集空间和关键渗流通道，直接关系到油气田能否持续高产、稳产，并且影响着油气田的最终采收率。能否对裂缝的分布规律和发育特征进行可靠识别预测，是碳酸盐岩裂缝型油气藏钻探开发的关键。

近年来，中国塔里木盆地、四川盆地在深部碳酸盐岩地层发现多个亿吨储量油气田，成为下步勘探开发的重点。碳酸盐岩地层钻进过程中由于其裂缝发育导致漏塌等复杂时效较高，井下复杂情况频发，严重制约油气资源的效益开发。裂缝的有效识别是钻前、钻中及钻后技术措施制定的关键，因此，如何有效识别裂缝成为必须要解决的关键问题。

目前，采用三维数字成像技术可以准确描述三维裂隙的空间分布[1-3]，电成像测井资料可以实现精确刻画裂缝结构[4-5]，核磁共振测井资料能够刻画不同类型孔隙的分布范围，偶极声波测井资料可对裂缝进行有效性评价[6-7]。然而成本高、易受工况影响等缺陷使得上述方法难以广泛推广应用，研发一种低成本高精度的裂缝识别方法显得至关重要；基于常规声波测井资料识别裂缝，将大大节省成本、有利于推广应用。利用常规测井数据，已发展出多种方法对裂缝发育段进行识别[8-10]，但碳酸盐岩具有较强的非均质性，单一的常规储层裂缝识别方法易受工况影响导致可靠度低。以现场常规声波数据为基础，基于主成分分析法对不同尺度裂缝发育地层进行预测识别，消除不同裂缝识别方法之间存在的偏差以及工况的影响、提高预测精度，能够碳酸盐岩油气资源的勘探开发提供有效的技术支撑，降低钻井复杂时效，提高油气开发收益。

1 碳酸盐岩地层裂缝识别方法

碳酸盐岩地层中裂缝的存在会对常规测井数据造成不同的影响，如在裂缝发育段，声波测井会明显增大并出现周波跳跃，井径曲线表现出强烈的振荡扩径并出现椭圆井眼，电阻率双侧向曲线出现读数比致密层低等现象，以此可反演碳酸盐岩中的裂缝发育程度。常规储层裂缝识别方法往往只能从一个层面考虑裂缝对测井数据的影响，因此在复杂工况下容易出现偏差。目前常用的裂缝识别方法如下。

1.1 三孔隙度比值法

孔隙度是评价油气层、分析岩石成分、确定油气饱和度与渗透率等的一个重要参数，在碳酸盐岩油气藏中，以裂缝或溶洞为主的次生孔隙度对于油气流动至关重要。密度测井和中子测井主要反映的是地层总孔隙度，而声波测井则受裂缝影响较严重，主要反映了原生的粒间孔隙。利用声波时差计算孔隙度φS公式为

(1)

ACma=ACma1Vma1+ACma2Vma2

(2)

式中：ACma为岩石基质的声波时差；ACsh为泥质的声波时差；Vma1、Vma2分别为双矿物岩石中两种矿物的体积含量；ACma1和ACma2分别为双矿物岩石骨架声波时差；ACf为地层水声波时差；Vsh为泥质含量。

因此，在含裂缝地层中，3种孔隙度的比值X1可反映出次生孔隙的发育程度，X1越大说明裂缝或溶孔越发育，其计算公式为

(3)

式(3)中：φD为密度孔隙度；φN为中子孔隙度。

1.2 等效模量差比法

由于波速对地层密度反应较敏感，因此可计算地层等效弹性模量EC识别含气裂缝性地层，其计算公式为

(4)

(5)

式中：ECW为地层100%含水时的等效弹性模量；ρma为岩石基质密度；ρf为孔隙流体的密度；ρsh为泥质的密度；φ为孔隙度；ACw为地层水的声波时差。

当遇到含气裂缝地层时，密度测井值降低，声波时差增大，则等效模量差比X2>0，而在致密地层或含水层时，X2接近于0。

1.3 骨架指数法

由于声波测井和密度测井对于裂缝表现出明显的差异，通常可利用声波骨架指数和密度骨架指数的差异X3识别裂缝层段。

(6)

在裂缝发育层段，密度测井孔隙度大于声波测井孔隙度，则X3>0，而在致密层段，X3接近于0。

1.4 龟裂系数法

岩石中的纵波波速与岩石的完整程度有关。通过完整岩石的波速较快，而当岩石中发育高角度裂缝时，岩石中的波速明显降低[11-12]。因此利用岩石骨架与地层中传播速度之比X4可以反映地层中裂隙发育程度。

(7)

1.5 曲线变化率

碳酸盐岩地层中由于次生孔隙的存在，易发生井径扩大现象。随着成岩作用的进行，次生孔隙开始发育，总孔隙度随深度减小的趋势开始变缓。与此相对应，测井曲线随深度变化的梯度关系会发生变化，表现出直线的斜率发生改变。

裂缝的存在会引起测井响应的异常变化，采用五点平均法通过计算对裂缝较为敏感的声波时差AC、井径CL和自然伽马GR曲线的变化率X5，对裂缝进行指示。

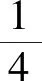
|Yj-Yj+1|+|Yj+1-Yj+2|)

(8)

式(8)中：Yj为3种曲线当前点测井值；Yj-2为当前深度处上2点测井值；Yj-1为当前深度处上1点测井值；Yj+1为当前深度处下1点测井值；Yj+2为当前深度处下2点测井值。

1.6 次生孔隙交会图法

由于声波时差基本上不反映次生孔隙，而密度、中子测井反映次生孔隙。利用孔隙度公式可求得次生孔隙度为

(9)

1.7 声波等效介质法

采用适用于测井尺度的DEM(differential equivalent medium)模型计算理论波速，将孔隙按纵横比AR分成3种：孔洞(AR=0.8)、粒间孔(AR=0.1)、裂缝(AR=0.05)。其中孔洞表示地层中坚硬的近圆形孔隙或溶洞，裂隙表示岩石中“最柔软”的孔隙，受到外力作用时易闭合，对岩石速度的影响较大。假设地层由两类孔隙组成(粒间孔+孔洞或裂缝)，并将DEM模型计算的结果与实际声波测井结果进行对比，通过迭代反演，确定各种孔隙所占比例及裂缝密度。

1.8 基于分形理论的处理方法

不同孔隙结构地层的测井声波具有不同的分形维数，利用分形方法表征常规测井曲线的变化程度，进而识别裂缝发育地层。选取对裂缝较为敏感的声波测井曲线和双侧向电阻率差异曲线，按式(10)计算每个采样点的R/S值，并将选取的曲线与采样点作双对数散点图，进而利用该曲线斜率Hu求取分形维数D。通常，地层裂缝越发育，地层非均质性越强，分形维数也会越大。

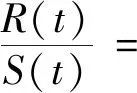
(10)

式(10)中：R、S为无因次的数据序列相对波动强度；t为数据点个数；i为测点序号；ζi为第i个测点的测井曲线值；<ζ>t为t个测点的期望值；α为尺度系数。

D=2-Hu

(11)

1.9 基于双树复小波的多尺度分析

在测井解释实践中，裂缝发育将会引起声波时差曲线出现小幅度摆动和时差增大现象，因此常利用声波时差的增大来定性识别缝发育井段。然而，在实际声波时差测井资料中，这种影响在原始测井曲线上常常不明显。采用多尺度处理方法，在合适的尺度上重构的高频信息以便能够突出裂缝发育层段声波时差起伏波动的特征，将有助于裂缝发育段的准确识别[13]。Kingsbury[14]提出了双树复小波变换(dual tree complex wavelet transform，DTCWT)的概念，是对传统离散小波变换(discrete wavelet transform，DWT)的增强。与实际正/负频带滤波的思路一致，DTCWT采用二叉树结构的DWT，包含两个平行的小波树，第一个小波树给出了变换的实部，而第二个小波树给出了虚部。相比传统的DWT，该方法具有更多优势：一是在二维或更高维度上具有移位不变性，输入信号的微小变化并不会引起小波系数的明显变化；二是具有方向选择性，在行和列方向上可以突出任意方向的信息；三是由于DWT小波系数是通过非理想的低通和高通滤波器迭代离散时间进行采样，这会导致大量的数据冗余度。DTCWT具有独立于分析尺度数的有限的冗余度。对于DTCWT，目前已设计了多种滤波器。对于具有n个深度点的测井曲线，使用两个平行的Q-shift小波滤波器同时对原始信号x(n)进行小波变换可得到不同尺度下的小波系数。

利用双树复小波变换(DTCWT)对地层声波测井曲线和双侧向电阻率曲线进行多尺度分解，得到不同尺度上的小波系数的曲线，原始信号被分解成多个小波系数d1～d3和低频趋势a。测井曲线的总能量为地层岩性、流体性质、微观孔隙结构等不同频率响应的信号能量之和，其中高频信息可识别出声波时差曲线的小幅波动，进而预测地层裂缝发育段。经过DTCWT处理后，测井曲线的纵向分辨率明显提高，有助于裂缝发育层段的识别。

2 基于主成分分析的裂缝识别方法

上述方法都能在一定程度上反映裂缝发育的井段，然而不同方法之间会存在一定的偏差，无法实现定量分析。碳酸盐岩具有较强的非均质性，单一的常规储层裂缝识别方法易受工况影响导致可靠度低。主成分分析是一种常用的降维方法，用于将多个可能相关变量转换为少量的主成分变量[15]。该方法可将一个多目标问题综合成一个单指标进行评价，避免了主观选择的随意性。因此，为更好地评价量化结果，采用PCA方法将多种方法得到的特征值进行降维，通过计算因子综合得分值对裂缝发育情况进行识别。

以三孔隙度比值X1、等效模量差比X2、骨架指数X3、龟裂系数X4、曲线变化率X5、次生孔隙度X6、有效介质裂缝密度X7、声波分形维数X8、双侧向异常分形维数X9、声波小波系数高频能量占比X10这10个参数作为变量计算指标变量矩阵A，进行主成分分析。其中声波分形维数和双侧向异常分形维数均为利用频谱分析和功率谱分析得到维数的平均值，声波小波系数高频能量占比为高频信息d1的能量。具体步骤如下。

步骤1 基于深度点建立指标变量矩阵A。对于每一个深度点的测井数据，基于上述基于深度点和波形处理的方法可得到M个特征参数，每个深度点可以得到一个M×1矩阵。对于N个深度点，使用A1,A2,…,AN表示这些深度点上M×1维度的列矩阵。

(12)

步骤2 将指标变量标准化为矩阵X。由于主成分是从协方差矩阵中得出，协方差矩阵受评价指标量纲和数量级的影响，不同的量纲和数量级会产生不同的协方差，首先需要对原始数据A进行标准化，使其平均值为0，标准差为1，便于不同单位或量级的指标能够进行比较和加权。

(13)

(14)

(15)

(16)

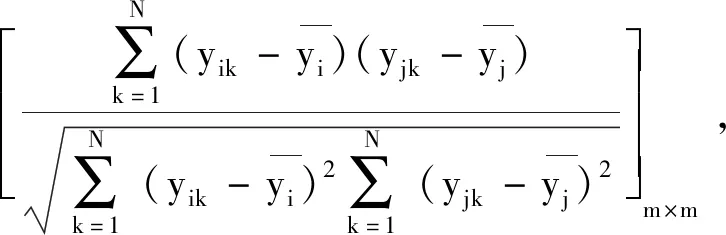
i,j=1,2,…,m

(17)

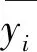
步骤4 求相关矩阵的特征根和特征向量。

|R-λE|=0

(18)

式(18)中：R和λ分别为相关系数矩阵和特征值；E为单位矩阵。

步骤5 计算各主成分的方差贡献率αi和累计方差贡献率α(k)，计算公式为

(19)

(20)

步骤6 计算综合得分Zi，其计算公式为

Zi=a1iX1+a2iX2+…+aniXn，

i=1,2,…,m

(21)

式(21)中：ani为深度点i处第n个评估变量的贡献率系数；Xn为标准化的第n个评估变量。

3 裂缝综合识别方法现场应用

以SHB-X井奥陶系灰岩地层测井资料为基础分别计算10个参数X1～X10，使用主成分分析法对其进行孔隙结构预测。表1为SHB-X井取芯井段的缝洞分析结果。将计算结果与取芯分析结果进行对比，并对没有取芯分析的井段进行缝洞预测，如图1～图3所示。

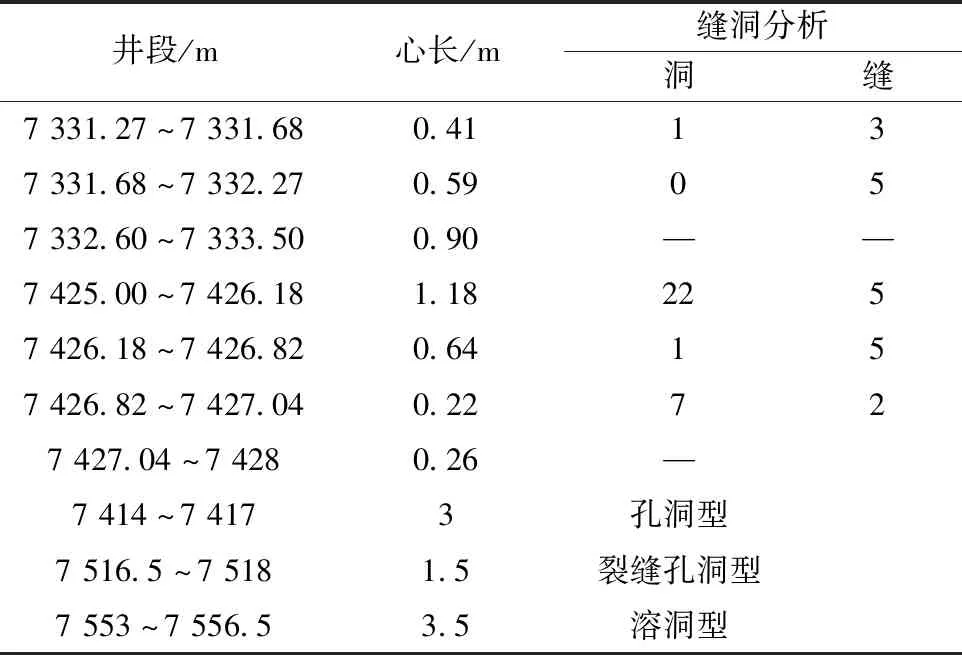
表1 SHB-X井取芯分析Table 1 Coring analysis of Well SHB-X

以7 370～7 410 m井段为例，SHB-X井一房间组上部地层缝洞欠发育，7 420～7 430 m深度段溶洞较为发育。鹰山组缝洞较为发育，在井径相对稳定段，7 510～7 525 m的深度范围内。按照主成分分析方法分别对裂缝发育层段进行识别，计算得到不同参变量的变化曲线如图1、图2所示。根据参变量与裂缝发育程度的关系，确定基于不同方法识别的裂缝发育层段，不同方法结果对比如图3所示。图2中红色线框的对照表明，主成分分析法的裂缝识别结果具有良好的可靠性和准确度。这主要是由于主成分分析方法综合了多种信息，避免了少数变量出现偏差时对整体结果稳定性的影响。

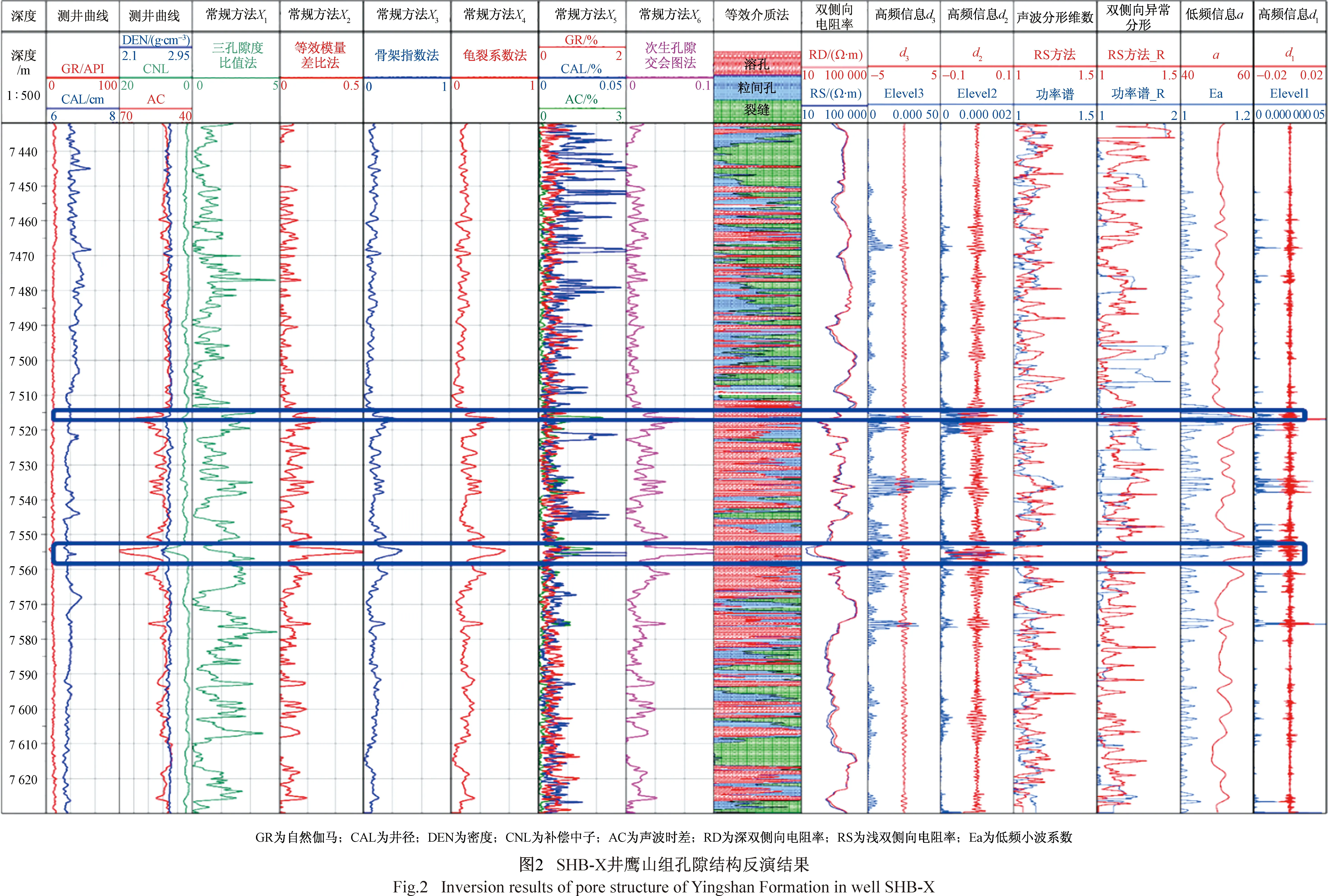
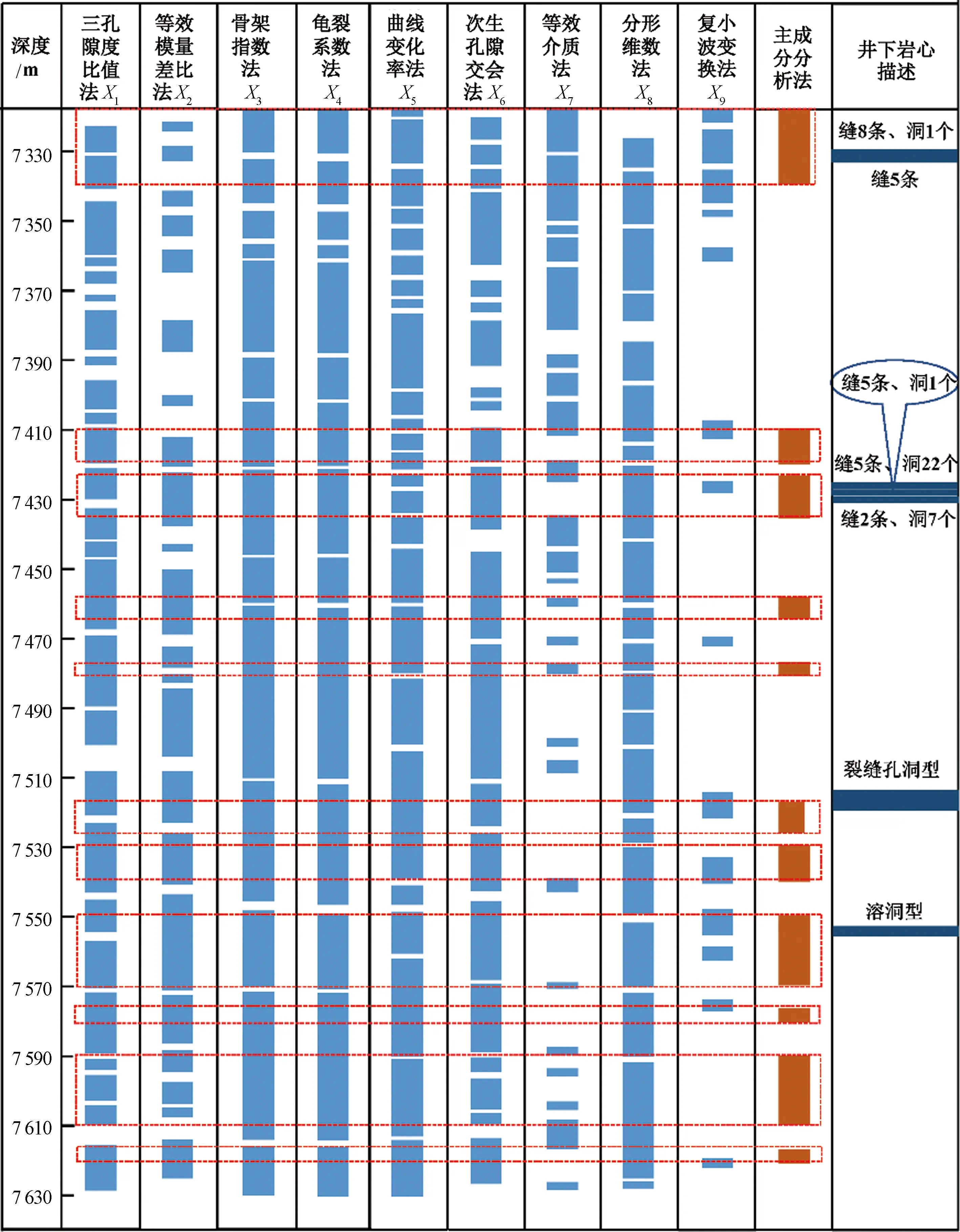
图3 SHB-X井一间房组及鹰山组主成分计算结果Fig.3 Principal component calculation results of Yijianfang and Yingshan Formation in SHB-X

4 结论

采用三孔隙度比值法、等效模量差比法、骨架指数法、龟裂系数法、曲线变化率、次生孔隙交会图法、声波等效介质法、基于分形理论的处理方法、基于双树复小波的多尺度分析等多种储层裂缝识别方法，对常规声波测井资料进行计算分析，求解各类方法中表征裂缝发育程度的特征值。在上述分析结果的基础上基于主成分分析法，对不同方法的裂缝识别结果进行综合考量、降维分析，消除不同裂缝识别方法之间存在的偏差以及工况的影响，得出裂缝表征综合量化值，实现对裂缝识别的定量分析预测。

根据塔里木盆地奥陶系碳酸盐岩地层测井资料以及取芯资料，对上述裂缝识别方法进行分析验证。识别结果与岩心结果有较强的一致性，并可在未取芯层段进行裂缝发育的预测。结果表明基于主成分分析的碳酸盐岩裂缝识别方法，能够基于常规声波测井资料对碳酸盐岩地层不同尺度裂缝发育程度进行定量预测，预测结果准确可靠。该方法基于常规声波测井资料进行计算分析，具有低成本高精度的优点，便于现场应用推广，满足低油价背景下大力勘探碳酸盐岩储层的工程需求。