基于线性自抗扰与重复控制的虚拟同步发电机并网逆变器控制策略

吕 聪，何 山,2*，王维庆,2，陈 伟，孔令清，王喜泉

(1.新疆大学电气工程学院，乌鲁木齐市 830049；2.可再生能源发电与并网控制教育部工程研究中心，乌鲁木齐市 830049)

近年来，分布式新能源发电在电力系统中的渗透率逐年提高，其中并网逆变器是实现DC-AC转换的电力电子器件，也是连接分布式电源和电网的核心设备[1-2]。电力电子器件使系统整体的惯性、阻尼降低，影响系统的稳定性[3-4]。为此，中外学者提出了虚拟同步发电机(virtual synchronous generator,VSG)的概念，通过控制并网逆变器模拟同步发电机的特性，为系统提供惯性和阻尼[5-6]，进而改善分布式电源并网的电能质量并提高并网运行的鲁棒性。

文献[7]参照同步发电机的数学模型以及调压、调频特性提出电压型VSG控制，能模拟同步发电机的外特性，具有较好的控制性能；文献[8]将VSG控制与自适应下垂控制结合应用于多端柔性直流系统中，满足惯性支撑的同时调整电网间不平衡功率的分配，但未考虑故障下所提策略的适用性；文献[9]提出了在电力电子变压器网侧整流级采用VSG控制，使级联模块具有惯性、阻尼，从而获得更好的动态性能来满足直流电压平衡的需要；文献[10]提出了基于VSG的自调节虚拟阻抗控制，通过改善阻尼限制过载和故障期间的故障电流，但需要持续搜索最佳参数，计算时间长；文献[11-12]提出基于自适应虚拟转动惯量的VSG控制策略，提升了动态响应速度，但动态响应过程中会有较大的有功功率振荡；文献[13]提出一种对补偿环节可调参数调节的改进VSG控制策略，通过降低系统阶数来抑制动态响应中的功率振荡；文献[14]根据故障时VSG故障电流在d、q坐标系下的特点，设计一种电流指令方法来抑制不平衡故障下的负序电流，使VSG在故障情况下也能安全稳定运行。上述基于VSG的逆变器并网大多采用基于PI(proportional-integral)的电压电流双闭环控制，具有控制结构简单、易于实现的优点。但在强耦合、高精度控制等场合有很大的局限性，且会引起相位滞后[15-16]，使VSG功率环路的带宽受到限制，导致控制性能变差，响应时间变长。此外，在电网发生扰动时也不能很好地抑制功频、电流的波动[17]。因此，研究具有高带宽、良好的抗扰能力、动态响应速度快的控制策略，对基于VSG的逆变器并网控制是非常重要的。

文献[18]提出的自抗扰控制(active disturbance rejection control,ADRC)具有动态响应快、抗干扰能力强的优点，可以很好地满足基于VSG的逆变器并网控制的要求，但其配置参数复杂，而高志强教授提出的线性自抗扰控制(linear active disturbance rejection control,LADRC)降低了参数配置的复杂度，已被广泛应用于工程实践中[19]。LADRC在满足上述基于VSG的逆变器并网控制要求的同时却牺牲了一定的跟踪精度，使用内模原理的重复控制(repeat control,RC)可有效消除输出稳态跟踪误差[20]，LADRC结合RC，可以弥补LADRC牺牲的跟踪精度。基于上述分析，提出线性自抗扰控制与重复控制相结合作为电压外环控制，电流内环仍采用PI控制的新型双闭环控制策略。其中线性自抗扰控制加快系统的动态响应速度且抗干扰能力强，重复控制提高双闭环控制的跟踪精度。在MATLAB/Simulink平台下搭建仿真模型，在功率扰动和三相短路故障下验证所提控制策略的可行性和有效性。

1 VSG的基本控制策略

图1为基于VSG的逆变器并网主电路拓扑和相关控制策略示意图，将蓄电池、光伏等分布式电源等效为直流电源Udc，基于VSG的逆变器经LC滤波电路和传输线连接到电网。

基于VSG的逆变器并网数学模型为

(1)

(2)

式(1)中：t为时间；R、L、C为滤波电路中的滤波电阻、电感、电容；iLk、igk分别为iLabc、igabc的相电流，k=ab,bc,ca；Uok、UCk分别为Uoabc、UCabc的相电压，k=ab,bc,ca。

将式(1)、式(2)左乘Park矩阵可得

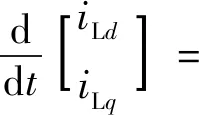
(3)

(4)

式中：iLf、igf分别为iLabc、igabc的d、q分量，f=d,q；Uof、UCf分别为Uoabc、UCabc的d、q分量，f=d,q；ωn为电网同步角速度。

Em为虚拟励磁电动势的幅值;θ为电角度;Pe、Qe分别为VSG的并网有功、无功功率;VT1～VT6为6个功率开关器件;Vd、Vq分别为虚拟励磁电动势的d、q轴分量;UVd、UVq分别为虚拟阻抗上压降的d轴、q轴分量;UCd、UCq分别为电容电压的d、q轴分量;Udref、Uqref分别为VSG输出的虚拟励磁电动势与虚拟阻抗上压降的差值的d、q轴分量;iLd、iLq分别为电感电流的d、q轴分量;分别为外环d轴、q轴电流实际值;Labc、Cabc、Rabc分别为滤波电路中的三相滤波电感、电容、电阻;SVPWM(space vector pulse width modulation)为空间电压矢量;SOGI(second-order general integrator)为二阶广义积分器图1 VSG并网示意图Fig.1 Sketch map of a grid-connected VSG

先对式(4)求导，再将式(3)代入其中，得

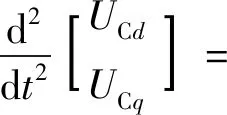
(5)

VSG的有功-频率控制方程为

(6)

式(6)中：J为虚拟转动惯量；D为虚拟阻尼系数；Pref、Pe分别为VSG有功功率参考值、并网有功功率；ω为虚拟转子角速度；θ为电角度。

有功功率控制框图如图2所示。

图2 有功频率控制框图Fig.2 The control block diagram of frequency

无功-电压控制方程为

(7)

式(7)中：Em为虚拟励磁电动势的幅值；Ugm、UCm分别为并网电压的幅值、电容电压的幅值；K0为无功-电压控制下垂系数；Qref、Qe分别为VSG无功功率参考值、并网无功功率；K1为比例系数。

1/s为积分图3 无功电压控制框图Fig.3 Control block diagram of reactive power

无功电压控制框图如图3所示。由于微电网线路呈阻性，而将VSG输出的虚拟励磁电动势Vabc与虚拟阻抗上压降Uvabc的差值作为电压电流双闭环中电压外环的参考值，能使系统呈一定感性，提高基于VSG的逆变器并网运行的鲁棒性，其控制框图如图4所示。

Ls为虚拟电感；Rs为虚拟电阻图4 引入虚拟阻抗控制框图Fig.4 Control block diagram of virtual impedance

可见，求解虚拟阻抗中电抗的压降需要对电网电流求导，且此微分环节将使得系统动态响应时间变长。由此引入基于广义二阶积分器(second-order general integrator,SOGI)的虚拟阻抗环节[21]，在计算其压降时，能避免微分运算，加快系统的动态响应。具体实现方式为：若Iin为输入正弦量，则输出Iout1与Iout2可表示为

(8)

式中:B为一常数。

由式(8)得

(9)

则虚拟电感Ls上的压降为

(10)

同理可得虚拟电阻Rs上的压降为

UR=RsIin=RsIout1

(11)

虚拟阻抗上的压降Uv为

Uv=UR+UL

(12)

由式(8)～式(12)得基于SOGI的虚拟阻抗框图(图5)。

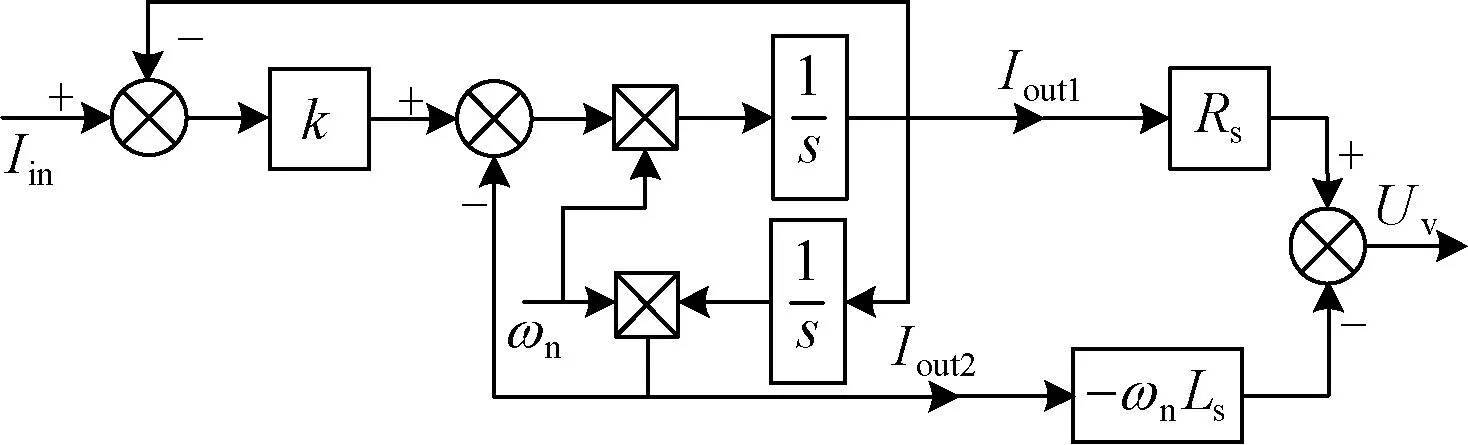
图5 基于SOGI的虚拟阻抗框图Fig.5 Block diagram of virtual impedance based on SOGI

引入基于SOGI虚拟阻抗的电压外环控制方程为

(13)

电流内环控制方程为

(14)

式中：Udref、Uqref分别为VSG输出的虚拟励磁电动势与虚拟阻抗上压降差值的d、q轴分量；UCd、UCq、ILd、ILq分别为电容电压、电感电流的d、q轴分量；Kp1、Ki1为电压外环PI控制参数；Kp2、Ki2为电流内环PI控制参数。

2 二阶LADRC+RC电压外环设计

由式(5)可知，基于VSG的逆变器并网系统是多变量、强耦合的，在精度要求较高的情况下，基于PI的电压电流双闭环控制已不再适用于并网，需设计新型双闭环控制策略来控制基于VSG的逆变器并网。LADRC根据跟踪误差调整其增益，从而与PI控制相比，加快系统的动态响应，通过补偿系统的不确定性和非线性，抑制系统的稳态扰动。然而作为一个线性控制器，采用LADRC的电压外环控制并不能显著提高跟踪精度，为提高其电压外环控制的跟踪精度，可在其中结合RC。由此提出一种采用LADRC+RC的电压外环控制，电流内环仍采用传统PI控制的新型双闭环控制策略。

2.1 二阶LADRC设计

LADRC由线性扩展状态观测器(linear extended state observer,LESO)和线性状态误差反馈律(linear state error feedback,LSEF)组成，其控制框图如图6所示。其中LESO的作用是估计总扰动；LSEF的功能类似线性PD控制器，获得所需信号；且LADRC的自抗扰效果主要取决于LESO对总扰动的估计精度。

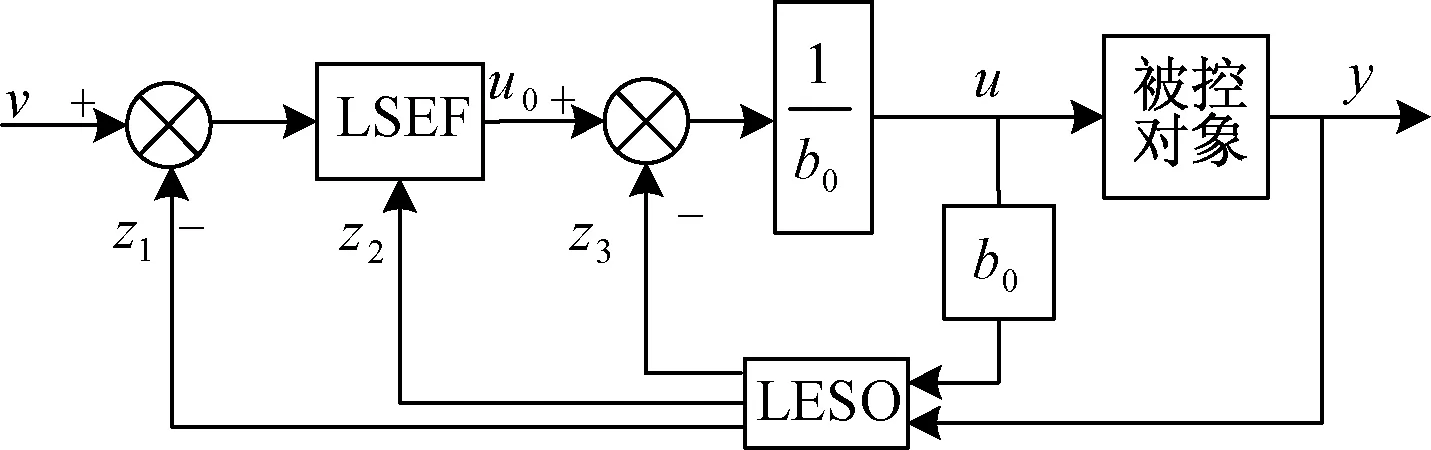
v为系统的输入;z1、z2、z3分别为对状态变量xi(t)的估计值，i=1、2、3;u0、u分别为LESF的输出、LADRC的输出;y为系统的输出图6 二阶LADRC控制框图Fig.6 Control block diagram of second-order LADRC

式(5)为时域二阶数学模型，因此需设计LADRC控制器的阶数为2，且式(5)中d、q轴形式相同，则LADRC控制结构也一致，所以可将d、q轴微分方程表示为一个通用的状态空间模型。

(15)

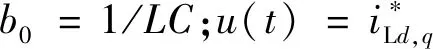
(16)

LESO为

(17)

式(17)中：zi(t)为对xi(t)的估计值，i=1,2,3；βi为观测器增益，决定了zi(t)对xi(t)估计精度；e(t)为状态变量xi(t)与估计值zi(t)的误差。

LSEF为

(18)

式(18)中：v(t)为LADRC的控制输入，v(t)=Ud,qref；kp、kd为LSEF的控制参数；观测器增益βi以及kp、kd可以通过带宽参数化方法得到，可表示为[19]

(19)

式(19)中：ω0为观测器带宽；ωc为控制器带宽。

2.2 RC设计

RC主要包括重复控制内模、周期延迟环节及补偿器，其控制框图如图7所示。在RC的作用下，累积周期内的误差，经补偿器后使RC能控制下一周期的输出量，从而减少总体误差。

RC的内部模型M可表示为

(20)

C(z)=krS(z)

(21)

式(21)中：kr为重复控制器增益，取kr=0.9；S(z)为二阶滤波器，主要作用是消除高次谐波。

S(s)为S(z)的拉普拉斯变换方程，可表示为

(22)

式(22)中：s为拉普拉斯变换中的微分算子；ω1为S(s)的截止频率，与VSG并网逆变器的截止频率相同；ξ为阻尼比，取ξ=0.707。

Q(z)Z-N为重复控制的改进内模；Q(z)起保持系统稳定的作用，一般为低通滤波环节或小于1的常数，取Q(z)=0.95；Z-N为周期性的延迟环节，其中N为基波周期内的采样次数，N等于采样频率与电网频率的比值；C(z)为补偿器，用于提供幅值补偿和相位补偿图7 RC控制框图Fig.7 The control block diagram of RC

将式(22)进行双线性变换，可得离散后的传递函数S(z)为

(23)

2.3 LADRC+RC复合控制策略

LADRC+RC电压外环控制、电流内环PI控制框图如图8所示。当系统稳定运行时，在LADRC+RC电压外环中，电压参考值与电容电压值的d、q轴分量分别做差，经LADRC+RC电压外环控制得到电流内环的参考值；在电流内环中，电流参考值与电感电流值的d、q轴分量分别做差，经PI控制后得到电压控制量。

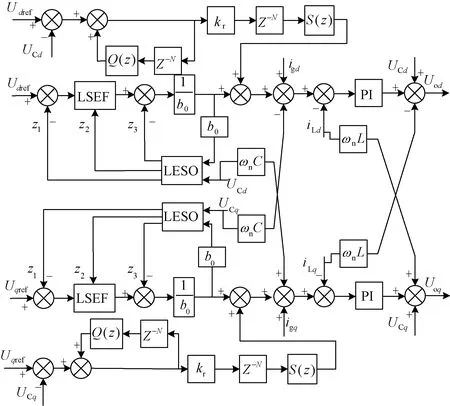
图8 LADRC+RC复合控制框图Fig.8 The composite control block diagram of LADRC and RC

此复合控制策略结合了LADRC与RC的优点，能同时获得更快的动态响应速度和更高的跟踪精度。图8中外环控制仍主要基于LADRC，保证并网的动态响应速度，且新增的RC减小了参考值与实际值之间的稳态误差，从而提高了跟踪精度。由于LADRC的等效带宽比RC大，因此可在不损害双闭环控制性能的情况下结合这两种控制策略。

3 仿真分析

在MATLAB/Simulink环境下，按照图1搭建基于VSG的逆变器并网系统模型，对比基于LADRC+RC的电压外环与电流内环PI控制策略(以下简称LADRC+RC双闭环控制策略)、基于LADRC的电压外环与电流内环PI控制策略(以下简称LADRC双闭环控制策略)和电压电流双闭环PI控制策略(以下简称PI双闭环控制策略)3种控制策略的性能，验证所提LADRC+RC双闭环控制策略的有效性及优越性。仿真模型的关键参数如表1所示。

表1 VSG仿真关键参数Table 1 Key parameters of VSG simulation

3.1 功率扰动下基于VSG的逆变器并网仿真分析

为验证所提LADRC+RC双闭环控制策略在功率扰动下的控制性能，设置0.6 s后VSG给定参考功率发生扰动，由10 kW跃变为15 kW，仿真结果如图9～图11所示。

图9 3种控制策略下功率扰动时的电网电流波形Fig.9 Current waveform during power disturbance under three control strategies

为更加直观地对比PI、LADRC、LADRC+RC这3种双闭环控制策略在功率扰动下的控制性能，对图10、图11中仿真结果进行量化，结果如表2、表3所示。

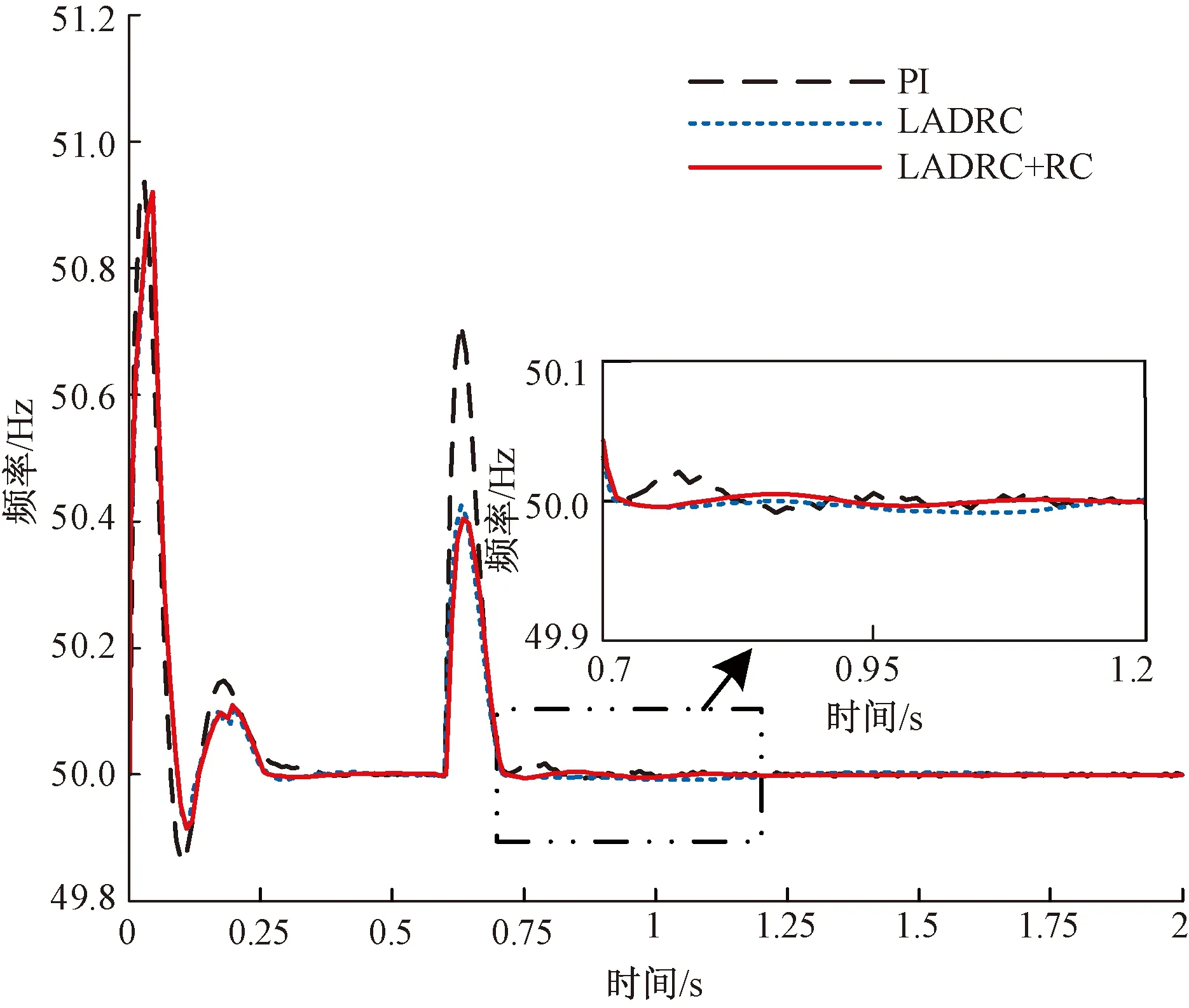
图10 3种控制策略下功率扰动时的频率比较Fig.10 Comparison of frequency during power disturbance under three control strategies

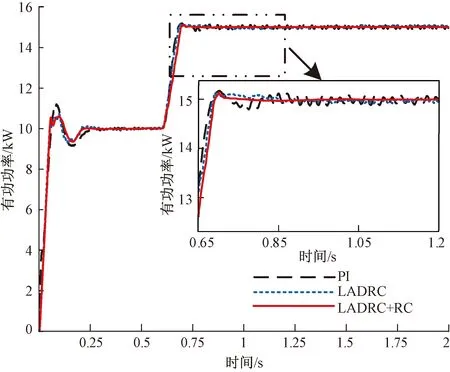
图11 3种控制策略下功率扰动时的有功功率比较Fig.11 Comparison of active power during power disturbance under three control strategies

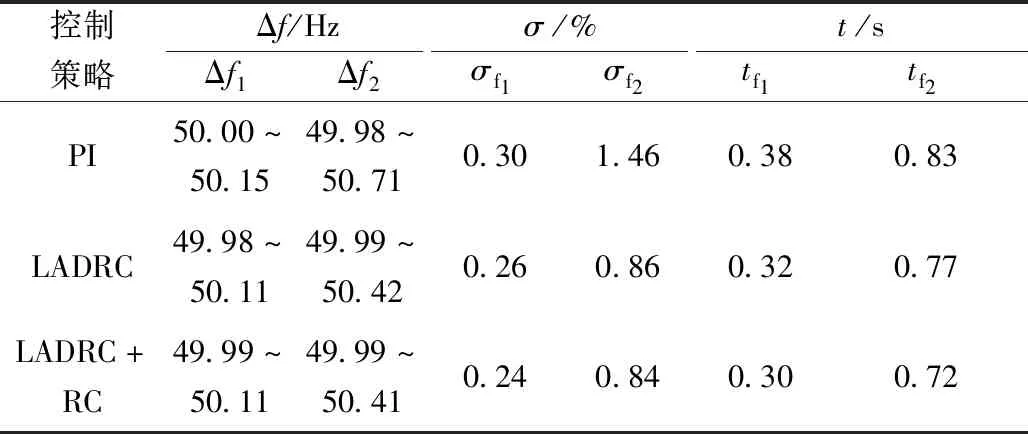
表2 功率扰动下频率波动及响应时间指标Table 2 Frequency fluctuation and response time index under power disturbance

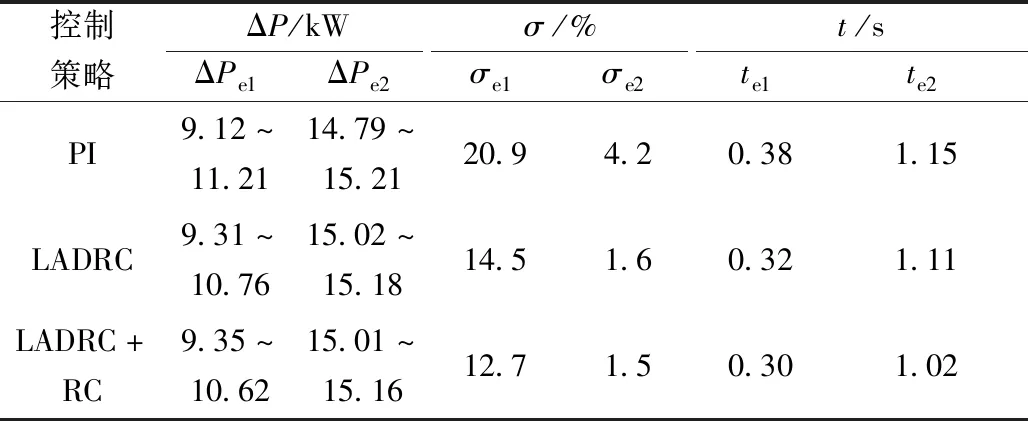
表3 功率扰动下有功功率波动及响应时间指标Table 3 Active power fluctuation and response time index under power disturbance

由图10、图11和表2、表3可知，基于VSG的逆变器并网启动时会有一定的冲击，经短暂波动后，采用LADRC+RC、LADRC双闭环控制策略分别在0.30、0.32 s时达到稳态，而PI双闭环控制策略在0.38 s时才达到稳态；与PI双闭环控制策略相比，LADRC+RC、LADRC双闭环控制策略的频率、有功功率波动误差指标σ都较小，抗干扰能力强。

如图9所示，LADRC+RC、LADRC双闭环控制策略的动态响应时间明显少于PI双闭环控制策略，电网电流在0.6 s功率增加后能快速进入新的稳态。由图10、图11、表2、表3可知，在0.6 s功率增加后LADRC+RC、LADRC双闭环控制策略的抗干扰能力强，能很好地抑制频率、有功功率波动，明显优于PI双闭环控制策略；且LADRC+RC双闭环控制策略的动态响应速度最快，仅在0.72 s就可达到稳态，比PI双闭环控制策略快0.11 s。在恢复稳定运行后，PI双闭环控制下的频率、有功功率在基准值上有微小波动，LADRC双闭环控制策略能抑制此微小波动，但略微偏离基准值，而LADRC+RC双闭环控制策略的跟踪精度高，能在抑制波动的同时使频率、有功功率紧跟基准值。

3.2 三相短路故障下基于VSG的逆变器并网仿真分析

为验证所提LADRC+RC双闭环控制策略在三相短路故障下的控制性能，设置0.8 s时基于VSG的逆变器并网线路发生三相短路故障，三相电压跌落至0.8 p.u.，1.2 s时故障切除，得到仿真结果如图12～图15所示。

图12 三相短路故障时电网电压输出波形Fig.12 Grid voltage output waveform when three-phase short-circuit fault occurs

为更加直观地对比PI、LADRC、LADRC+RC三种双闭环控制策略在电网三相短路故障时的控制性能，对图14、图15中仿真结果进行量化，分别如表4、表5所示。其中，Δf′、ΔP′分别为三相短路故障下频率、有功功率的波动范围，σ′为波动的误差量，t′为三相短路故障下的动态响应时间，Δf′1、ΔP′e1分别为基于VSG的逆变器刚并网时频率、有功功率的波动范围，σ′f1、σ′e1分别为对应的波动误差量，t′f1、t′e1分别为对应的动态响应时间，Δf′2、ΔP′e2分别为三相短路故障发生时频率、有功功率的波动范围，σ′f2、σ′e2分别为对应的波动误差量，t′f2、t′e2分别为对应的动态响应时间。Δf′3、ΔP′e3分别为三相短路故障切除时频率、有功功率的波动范围，σ′f3、σ′e3分别为对应的波动误差量，t′f3、t′e3分别为对应的动态响应时间。

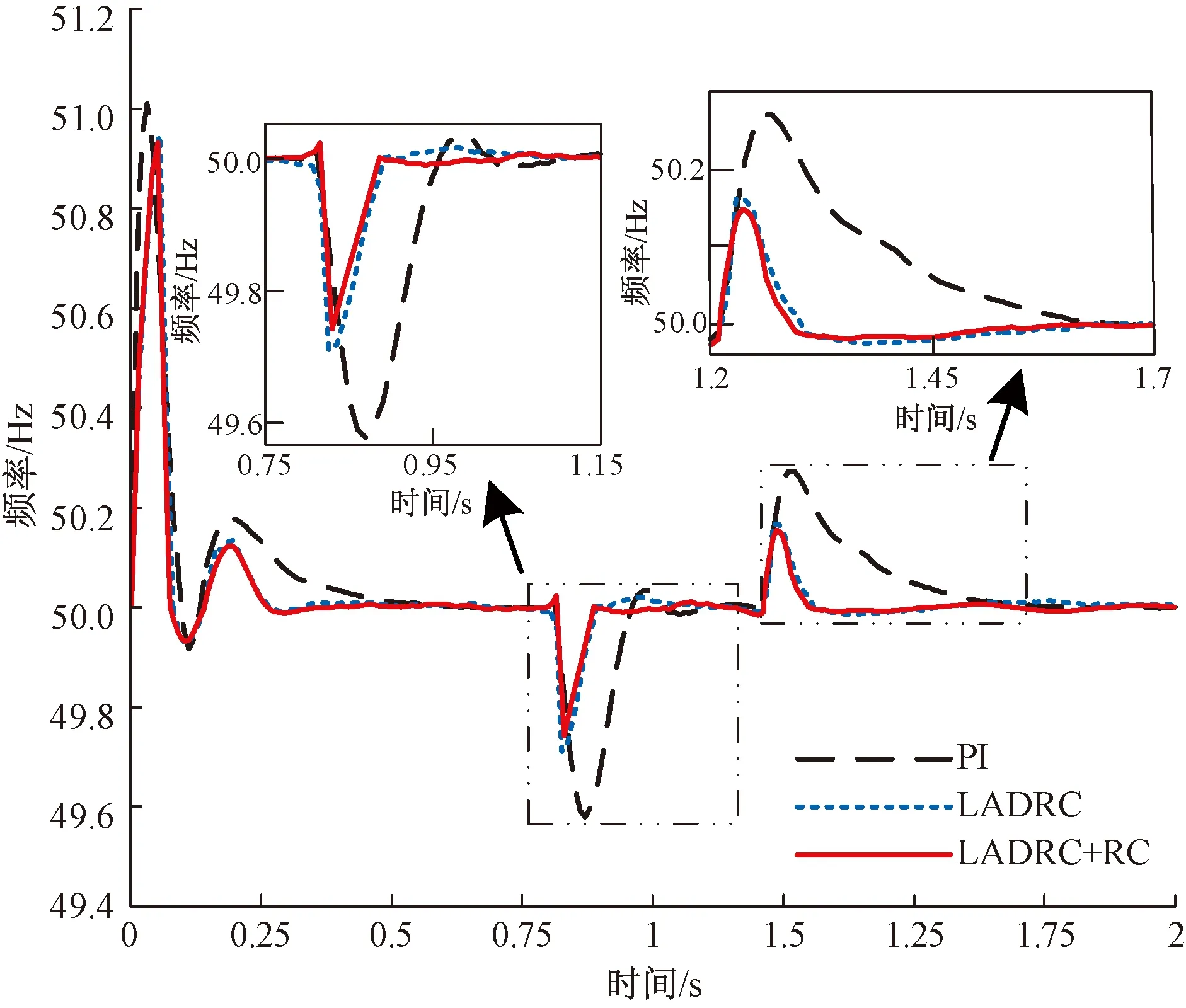
图14 3种控制策略下三相短路故障时的频率比较Fig.14 Comparison of frequency when three-phase short-circuit fault occurs under three control strategies

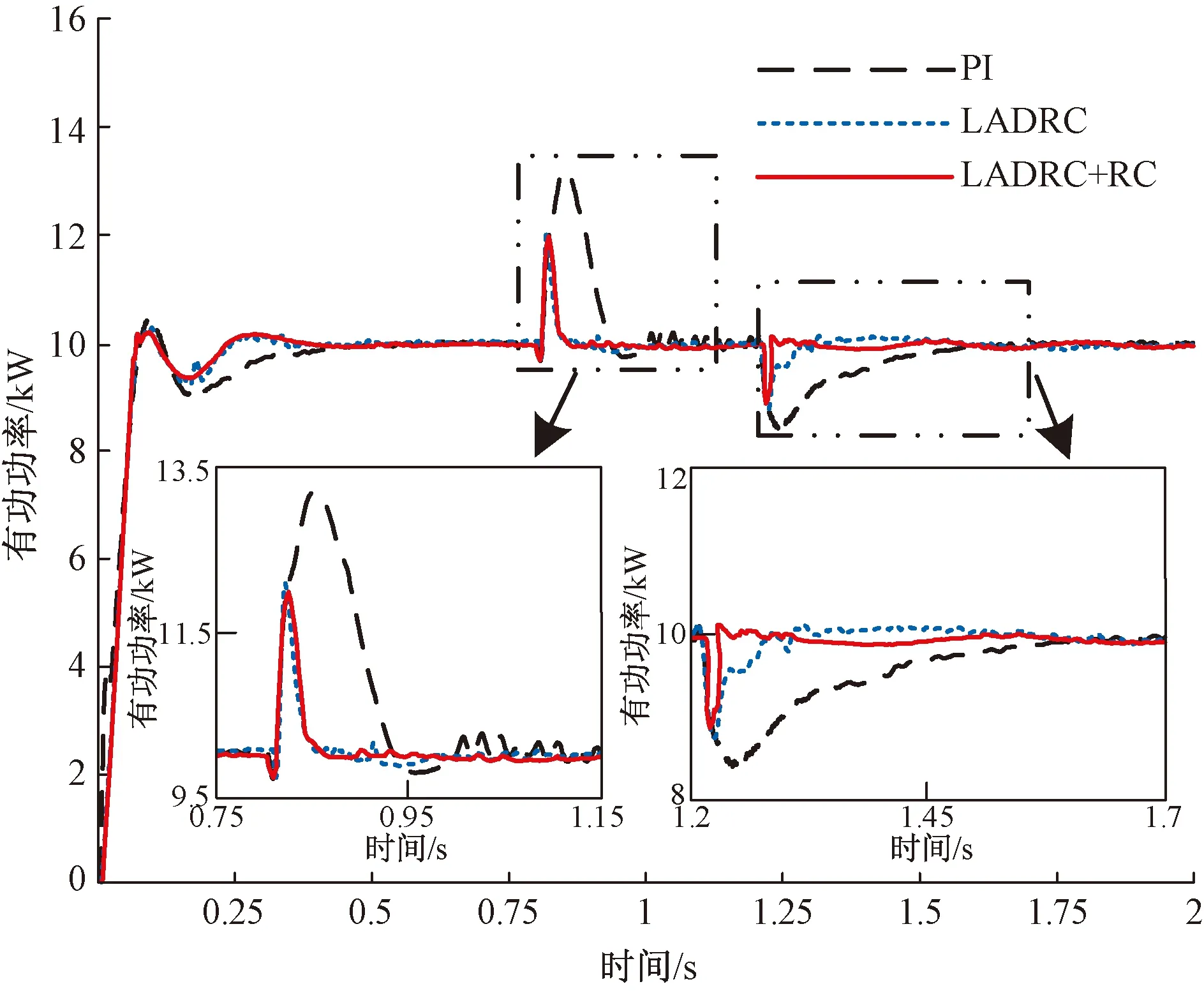
图15 3种控制策略下三相短路故障时的有功功率比较Fig.15 Comparison of active power during three-phase short-circuit fault under three control strategies

表4 三相短路故障时频率波动及响应时间指标Table 4 Frequency fluctuation and response time index when three-phase balance fault occurs

表5 三相短路故障时有功功率波动及响应时间指标Table 5 Active power fluctuation and response time index when three-phase balance fault occurs

如图13所示，在0.8 s发生故障时LADRC+RC、LADRC双闭环控制下的冲击电流都要远小于PI双闭环控制，且在故障发生时和故障切除后动态响应时间明显少于PI双闭环控制策略，电网电流均能快速进入新的稳态。由图14、图15和表4、表5可知，在0.8 s故障发生时LADRC+RC、LADRC双闭环控制策略的频率、有功功率波动误差小，抗干扰能力强，明显优于PI双闭环控制策略；且LADRC+RC双闭环控制策略的动态响应速度最快，仅在0.88 s就达到故障持续时间内的稳态，比PI双闭环控制策略快0.08 s。同理1.2 s故障切除后LADRC+RC双闭环控制策略的抗干扰能力最强、动态响应速度最快。在切除故障恢复稳定运行后，LADRC+RC双闭环控制策略能在抑制波动的同时紧跟基准值，具有较好的跟踪精度。

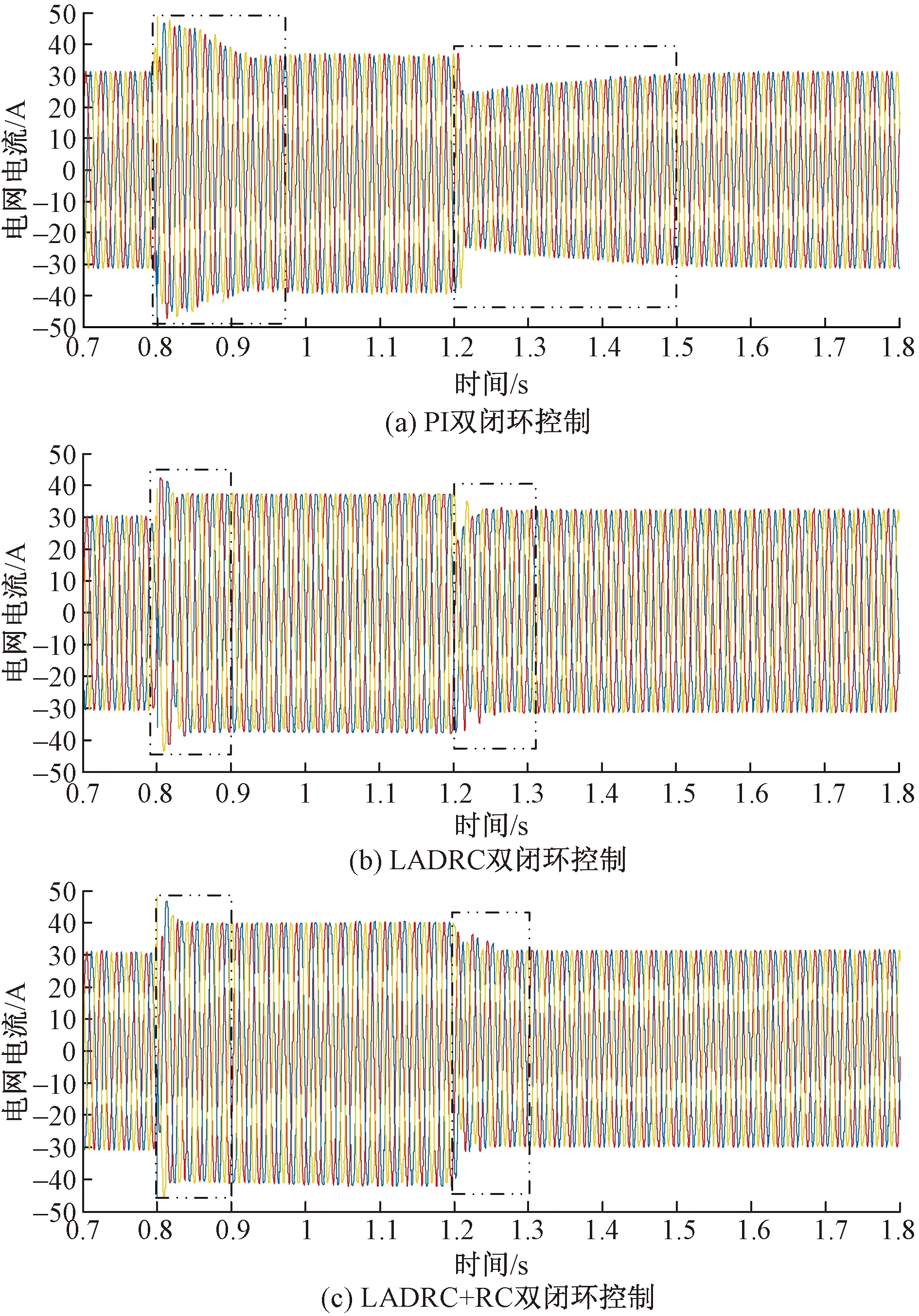
图13 3种控制策略下三相短路故障时的电网电流波形Fig.13 Grid current waveform during three-phase short-circuit fault under three control strategies

4 结论

基于VSG的逆变器并网采用电压电流双闭环PI控制策略，使系统动态响应时间长，抗干扰能力差的问题。结合线性自抗扰控制动态响应快，抗干扰能力强以及重复控制跟踪精度高的优势，提出线性自抗扰控制与重复控制相结合作为电压外环控制，电流内环仍采用PI控制的新型双闭环控制策略。功率扰动与三相短路故障下的仿真结果表明：对比电压电流双闭环PI控制策略，该策略动态响应速度加快、抗干扰能力强、跟踪精度高，从而使基于VSG的逆变器并网后能够安全可靠地运行。