滑坡碎屑流纵向作用下埋地天然气管道变形规律
2022-01-14麻宏强丁瑞祥陈海亮罗新梅王霁月朱烈忠王圣寻李安英
麻宏强 丁瑞祥 陈海亮 罗新梅 王霁月朱烈忠 谢 越 王圣寻 李安英
1. 华东交通大学土木建筑学院 2. 兰州理工大学土木工程学院
0 引言
随着国民经济的发展及工业化水平的提高,我国石油天然气的需求量逐步增大[1]。管道输送是目前最为经济有效的运输石油和天然气的方式,在全世界得到了广泛的应用,是关系国际民生的基础设施,集输管道的正常工作与生产生活密切相关。就油气长输管道而言,在地质灾害多发区,容易发生变形破坏,严重时会发生油气泄漏等安全事故,因而管道安全技术成为近几年研究的热点问题[2]。滑坡碎屑流作为滑坡灾害的一种,其滑坡体中含有较多碎石,且能以较高速度沿着山体运动,具有极强的破坏力[3-6]。对于滑坡区埋地集输管道灾变风险研究,目前主要以穿越滑坡体管道的位移变形、应力应变分布及各类因素对管道变形和应力应变的影响规律研究为主[7-10]。在这些研究中,主要采用解析法和数值法,如Rajani等[11-13]先后采用简单解析方法,利用弹性地基梁理论简化管土作用,分析了纵横向管道穿越滑坡作用的力学响应,得到纵向滑坡危险性小于横向滑坡的结论;梁政等[14-16]的相关研究也证明了这一点。随着计算机技术的提升,相关研究方法由解析法转变到数值法。相对于解析法,数值法可以考虑管土材料弹塑性材料特性和管土相互作用,进而得到管道受土壤性质、管道材料的影响规律,滑坡对埋地管道的影响作用计算结果也更符合实际[17-23]。如郝建斌等[21]在考虑管土相互作用过程分析的基础上,利用极限平衡法推导了横穿敷设情况下滑坡对管道推力的计算方法,并利用数值模拟验证了该计算方法的合理性。
实际工程中,受降雨、地震等因素的影响,产生的碎屑流流经埋地管道表面时,由于其通过土壤对管道的推挤或拖拽作用,导致埋地管道变形失效;而穿越滑坡体管道研究中的滑坡多数为蠕滑,即滑坡体使管道沿滑坡方向进行微小的移动,造成管道拉伸或者压缩变形。两者受力存在较大差异,埋地管道力学状况迥然不同,目前针对滑坡碎屑流灾害作用下埋地管道灾变影响方面的研究较少。因此,笔者基于热弹塑性理论和管道与土体非线性接触理论,采用管—土耦合方法,建立了滑坡碎屑流灾害作用下埋地天然气管道变形分析模型,分析了埋地集输管道的变形影响规律。
1 有限元模型分析
1.1 模型简化
小型滑坡碎屑流在土体表面滑动过程中,其堆积形态类似于半椭球体[24]。因此,将土体表面滑坡碎屑流运动过程中的堆积形态近似为半椭球体。图1是小型滑坡碎屑流在土壤表层作用示意图。
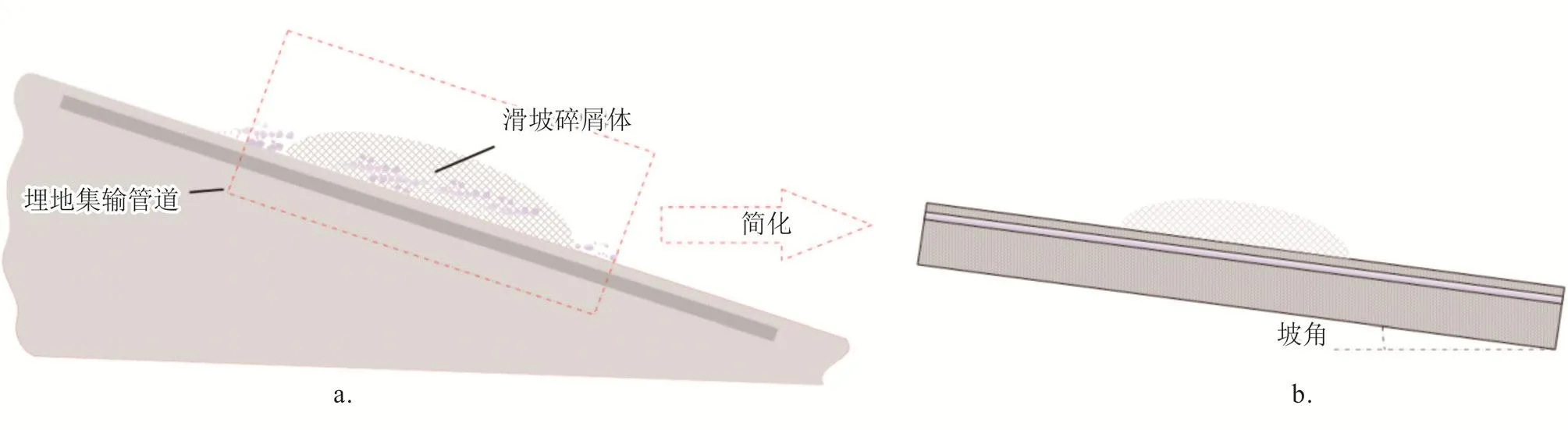
图1 滑坡碎屑在土壤表层作用示意图
依据滑坡碎屑流颗粒流理论,滑坡碎屑流流动是其底部剪力和自身重力共同作用的结果,所以,滑坡碎屑流对埋地集输管道顶层土体表面的作用可等效为其对土体表面的摩擦力和压力的作用。滑坡碎屑流对埋地集输管道顶层土体表面的作用力计算公式如下:
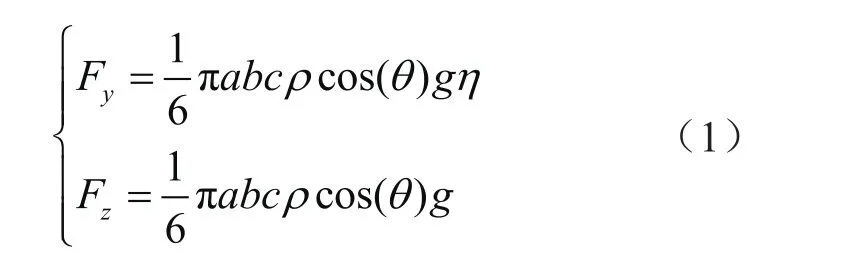
式中Fy、Fz分别表示滑坡碎屑流y、z方向上的等效作用力,N;a、b、c分别表示埋地集输管道顶层土体表面滑坡碎屑流的长、宽、高,m;g表示重力加速度,一般取9.8 m/s2;ρ表示滑坡碎屑流密度,kg/m3;θ表示坡体与水平夹角,(°);η为滑坡碎屑流与土体表面间的摩擦系数,依照岩土勘查工程手册设定为0.3[25]。
当埋地集输管道弯曲或受外部挤压作用时,管道横截面可能出现椭圆化变形,截面形状改变导致管道流体受阻或者内检测器无法通过。椭圆化变形率(Δθ)定义为:
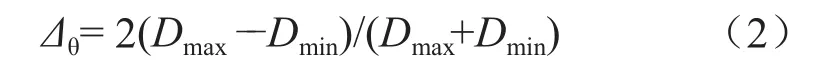
式中Dmax和Dmin分别表示集输管道最大和最小外径,m。为了保证埋地天然气管道的安全运行,管道椭圆化率需满足以下条件:

式中表示临界椭圆化变形率,一般通过分析或实验确定。
为便于分析,选取沿管长方向65 m、管道两侧宽度为30 m的管土区域进行集输管道变形分析。为减小埋地管道底层土体对模拟结果的影响,经大量试算将管道顶部距离底层土体的距离确定为6.2 m,图2是滑坡碎屑流纵向作用下埋地集输管道变形分析简化模型。
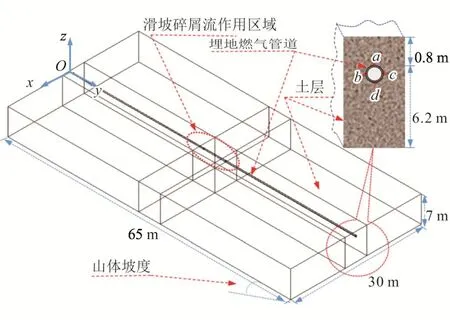
图2 滑坡碎屑流纵向作用下埋地集输管道变形分析简化模型图
同时,要进行滑坡碎屑流作用条件下埋地管道应变分析,还需要对管土材料、管土接触等做一定的合理假设,假设如下:
1)管道焊缝力学性能与管道母材相同,且为双折线理想弹塑性。
2)土体的力学性能为理想弹塑性。
3)管道与土体间的界面采用有限滑动非线性接触。
4)采用温度边界和压力边界代替管道内天然气作用。
5)滑坡碎屑流作用采用颗粒流模型简化成滑坡碎屑流自身重力和剪应力。
1.2 边界条件
采用有限元软件ANSYS建立管土作用模型,滑坡体作用等效为竖直方向的力和切向的力;ANSYS实体建模通过关键点、线、面和体构成几何模型,实体模型适用于庞大复杂模型,尤其适合三维实体模型,管道相应采用实体单元SOLID185,SOLID185三维实体单元具备超弹性、应力钢化、蠕变、大变形、大应变能力,且收敛效果良好,土壤单元采用SOLID65,SOLID65单元适合传统D—P模型,适合非线性材料,同时可以模拟塑性变形过程。
1)接触:管道与周围土壤作用选择更为精确的面面非线性接触模型,管土之间的界面采用有限滑动接触属性,管土之间接触采用库伦摩擦模型,考虑摩擦作用,设置管土之间摩擦系数为0.3。
2)边界约束:管道模型两端约束y方向,模拟远离滑坡区域管道轴向零位移;土壤底部全约束,管土轴向约束y方向,两侧约束x方向。
3)模型载荷:管道内部设置垂直于管壁面的压力(正常工况下为8.9 MPa),以模拟管线运行时的内部压力载荷;管道施加体温度328.7 K,模拟正常运行温度;考虑埋地集输管道纵向滑坡多发生在边坡处,管线铺设存在坡度,改变模型施加的重力加速度方向和大小模拟坡度的影响效果(某气田边坡处管线铺设坡度介于π/9~5π/18);滑坡区域施加滑坡作用等效载荷,沿y方向和z方向。
2 网格无关性及模型验证
2.1 网格无关性
有限元模型采用结构化网格划分,相比非结构化网格,结构化网格能以较小的网格数量达到较高计算精度,关键区域加密不影响整体网格质量。
按照网格数量划分为A、B、C、D类型,将径厚比(D/t)为323.9 mm/14.2 mm管道,在滑坡碎屑体长5 m、宽5 m、厚1 m、天然气温度328 K、运行压力8.9 MPa、坡度π/9、埋深0.8 m条件下,依据管道等效应力、等效应变对不同网格数量的计算误差、计算时间进行分析比较,结果如表1所示,得到A类型27万网格,应力、应变误差与更高网格数量工况相比,误差在2%以内,计算时间仅需2 h,满足计算精度要求,计算效率更高。
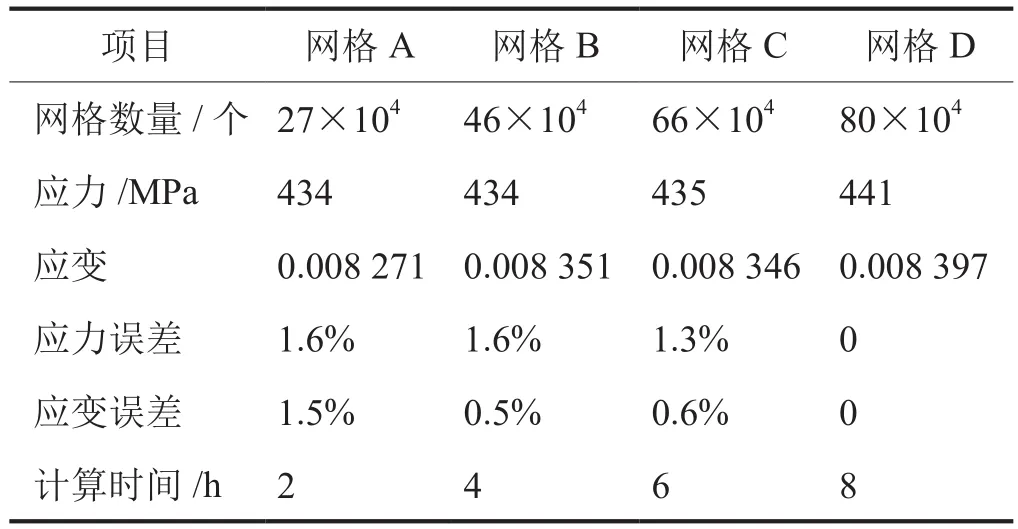
表1 网格无关性验证表
2.2 模型验证
采用普光气田现场监测数据对模型进行可靠性验证,由于监测安装时,埋地管道存在运行压力和运行温度,所以应变传感器监测到的应变数值并不是管道本身的应变值,而是管道运行工况的变动值。故选取当日管道运行压力波动值为1 MPa、管道运行温度变化差为10 ℃时的监测值。监测过程中,并未出现滑坡碎屑流情况,因此在模型验证过程中,选取Fz、Fy均为零;在管道埋深为0.8 m、坡度角为π/9、天然气温度为328 K,压力为8.9 MPa的条件下,选择管土模型y=25 m截面处管道轴向应变值与监测值进行比较,结果如表2所示。结果表明,监测应变和数值模拟工况的a、b、c处上的管道的轴向应变差异并不大,之间误差在10%以内,即数值模拟得到的结论基本是可靠的。
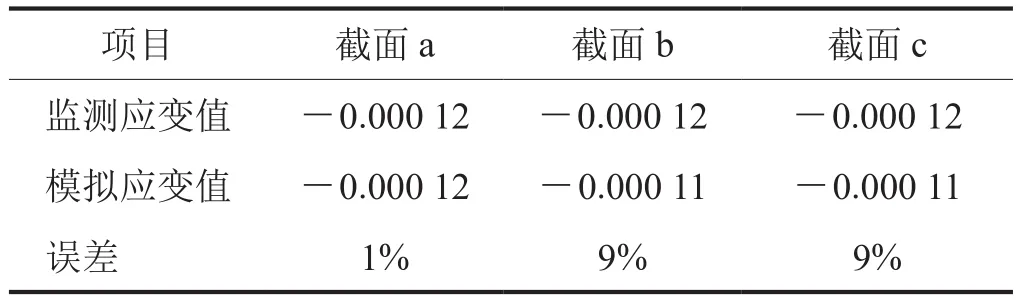
表2 监测与模拟工况对比表
3 结果与分析
3.1 最大椭圆化率变化规律研究
3.1.1 运行压力
图3 所示为在天然气温度为328 K、山体坡度为π/9、埋深为0.8 m、滑坡碎屑流长度为5 m、宽度为5 m条件下,D/t为323.9 mm/14.2 mm的管道最大椭圆化率随运行压力的变化规律。结果表明,滑坡碎屑流作用条件下,管道最大椭圆化率与管道运行压力负相关,管道椭圆化率随着运行压力的增加而减小,并且伴随滑坡碎屑流厚度(TH)的增加,管道最大椭圆化率的减小率也随之增加。TH为0.5 m时,随着运行压力的增大,管道最大椭圆化率降低了0.15%;TH为2.0 m时,最大椭圆化率降低了1.60%。由此可见,滑坡碎屑流作用条件下,较大运行压力在一定程度上可以起到增强管道抵抗变形能力的作用。
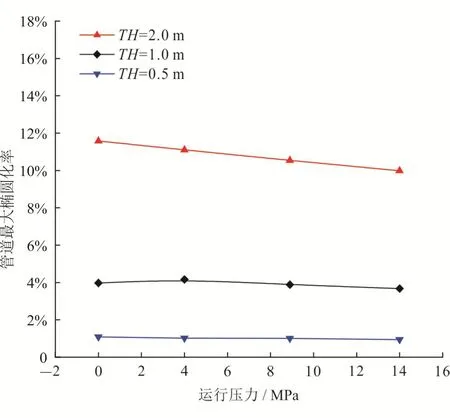
图3 管道运行压力与管道最大椭圆化率的关系图
3.1.2 管道温升
图4所示为在天然气温度为328 K、运行压力为8.9 MPa、山体坡度为π/9、埋深为0.8 m、滑坡碎屑流长度为5 m、宽度为5 m条件下,D/t为323.9 mm/14.2 mm的管道最大椭圆化率随运行温度的变化规律。结果表明,对于管道运行温度而言,滑坡碎屑流作用条件下,管道温升对管道最大椭圆化率的影响并不明显,整体看来,管道温升对管道最大椭圆化率影响较小。所以,运行温度并非是影响管道安全的主要影响因素。
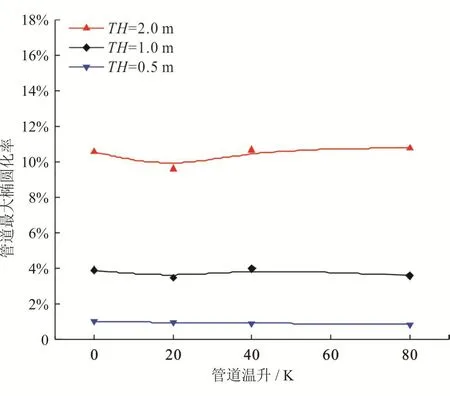
图4 管道温升与管道最大椭圆化率的关系图
3.1.3 管道径厚比
图5所示为天然气温度为328 K、运行压力为8.9 MPa、山体坡度为π/9、埋深为0.8 m、滑坡碎屑流长度为5 m、宽度为5 m时,不同TH条件下,管道最大椭圆化率随径厚比的变化规律。结果表明,随着径厚比的增加,管道最大椭圆化率也随之增加,增加趋势呈对数函数形式。也就是说,滑坡碎屑流作用条件下,对于同一管材,随着管道径厚比的增大,管道的失效风险也随之增加。其主要原因是随着管道径厚比的增加,管土的接触面积也随之增加,滑坡碎屑流将更多的作用力传递到管道上,而不是作用在管道周围的土体上。
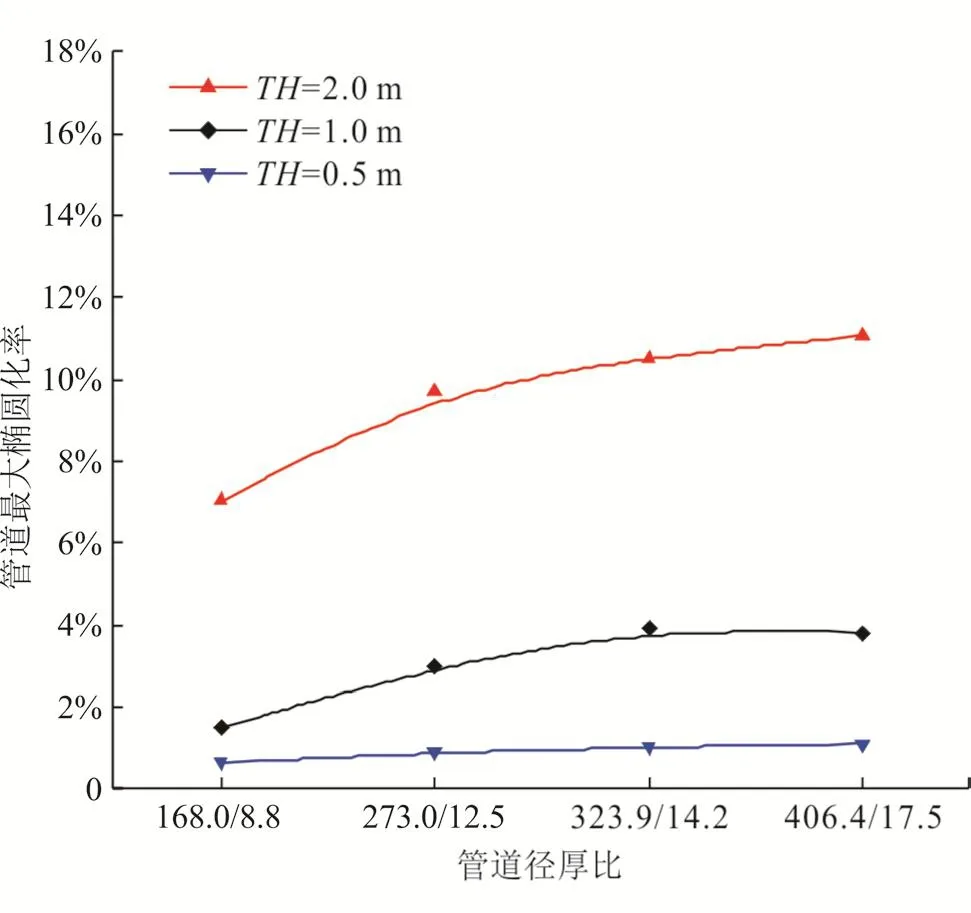
图5 管道径厚比与管道最大椭圆化率的关系图
同样,此处也可以得到,TH越大,管道最大椭圆化率随管道径厚比的变化率越大,径厚比对管道椭圆化率影响越明显,TH为0.5 m时,管道最大椭圆化率升高了0.48%;TH为2.0 m时,管道最大椭圆化率升高了4%。
3.1.4 壁厚减薄率
图6 所示为天然气温度328 K、运行压力8.9 MPa、山体坡度π/9、埋深0.8 m、滑坡碎屑流长度为5 m、宽度5 m时、厚度为2 m时,不同径厚比条件下,管道最大椭圆化率随管道壁厚减薄的变化规律。从图6可以看出,随着壁厚减薄加剧,不同规格管道的最大椭圆化率随之呈线性函数形式急剧增加,因而壁厚也是影响管道安全的重要因素,对于埋地管道应注意腐蚀防护,减小管道管壁减薄诱发的失效风险。
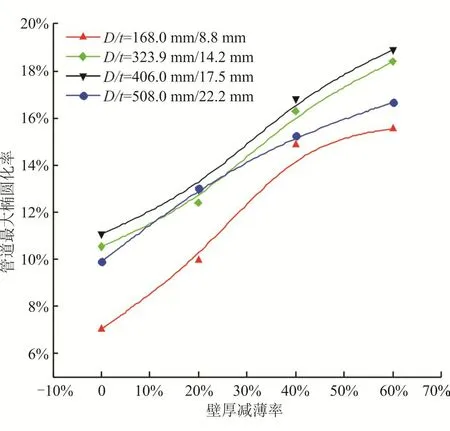
图6 管道壁厚减薄率与管道最大椭圆化率的关系图
3.2 敏感性分析
3.2.1 滑坡碎屑流规模特征系数对管道椭圆化率的敏感性
为了更好地研究滑坡碎屑流规模特征系数对管道最大椭圆化率的敏感性,将滑坡碎屑流的特征系数进行归一化处理,其公式为:
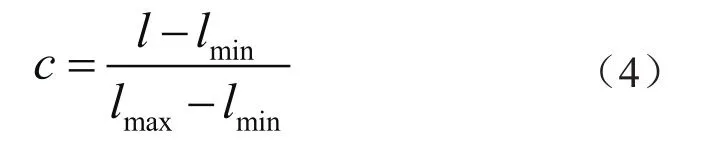
式中c表示特征系数;l表示特征参数的值;lmax和lmin分别表示模拟中所设定的特征参数的最大值以及最小值。
本节特征系数为碎屑流的厚度、长度和宽度。图7所示是天然气温度为328 K、运行压力为8.9 MPa、山体坡度为π/9、埋深为0.8 m时,管道最大椭圆化率随滑坡碎屑流规模特征系数的变化规律。结果表明,管道最大椭圆化率与滑坡碎屑流规模呈正相关;在同样的运行条件下,管道椭圆化率随滑坡碎屑流厚度增大而增长了14.2%,随长度和宽度增大而分别增长了9.9%和3.0%,也就是说对比滑坡碎屑流厚度、长度、宽度对管道最大椭圆化率影响,宽度影响程度最小,长度次之,厚度对管道最大椭圆化率的影响最大。
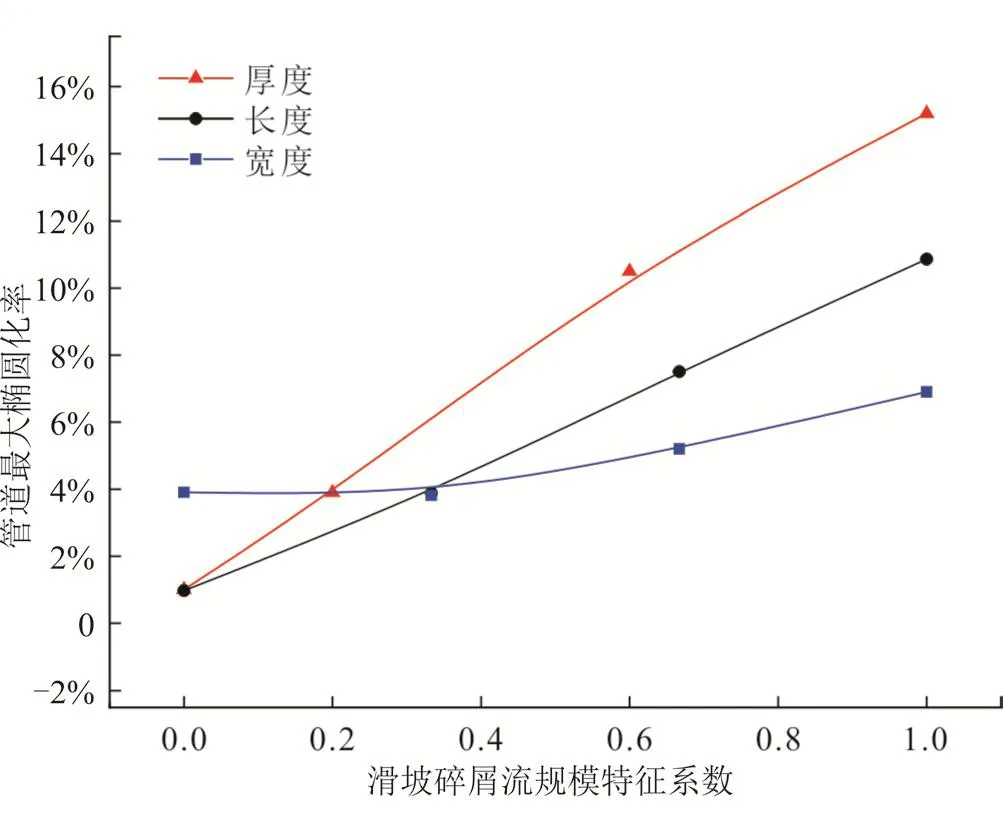
图7 滑坡碎屑流规模特征系数对管道最大椭圆化率的敏感性图
3.2.2 运行、结构特征系数对管道椭圆化率的敏感性
利用式(4)将天然气管道运行、结构特征系数进行归一化处理,得到了管道最大椭圆化率随各个特征系数的变化趋势(图8)。本节的特征系数为管道的运行压力、管道温升、径厚比和壁厚减薄率。如图8所示,管道最大椭圆化率与运行压力呈负相关,随着运行压力增大,管道最大椭圆化率降低了1.6%;与温升关系非常小,随温度升高管道最大椭圆化率增长了0.2%。管道最大椭圆化率与径厚比和壁厚减薄率呈正相关,管道最大椭圆化率随着径厚比和壁厚减薄率增大而分别增长了4.0%和7.9%。显然,在滑坡碎屑流作用条件下,管道最大椭圆化率受运行参数的影响较小,受管道自身结构的影响更大。因此,在满足天然气管道强度要求条件下,合理设计结构,适当提高管道运行压力,可以减小埋地天然气管道失效的风险,提高其安全性。
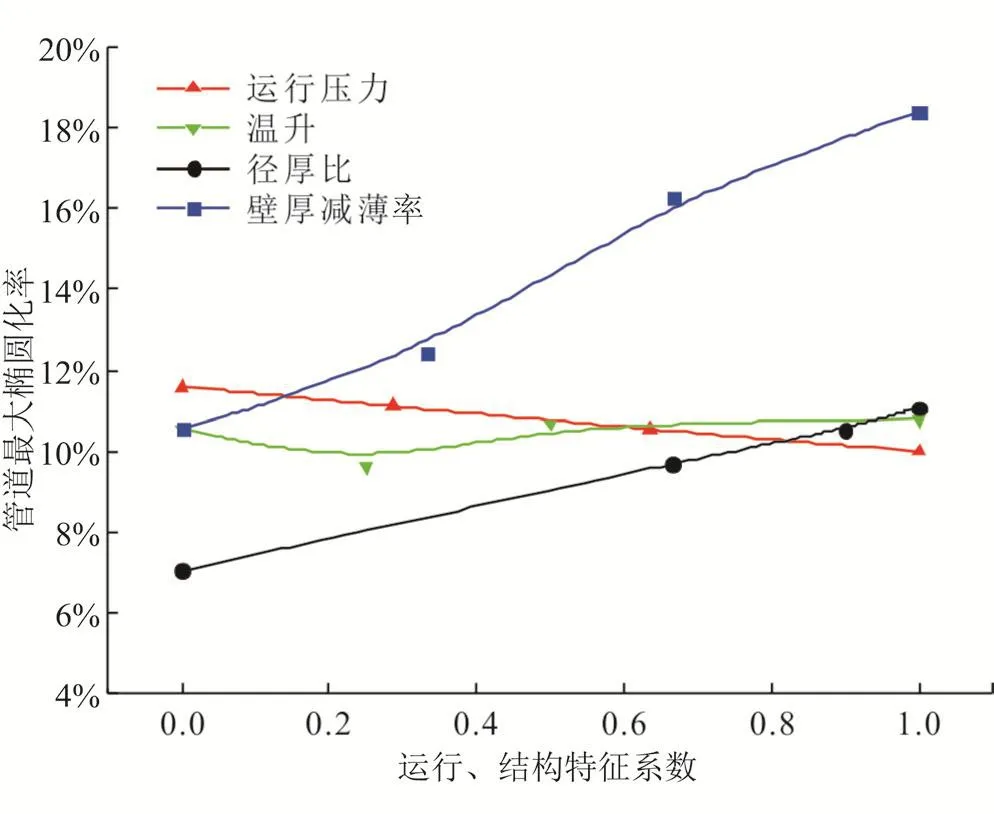
图8 运行、结构特征系数对管道最大椭圆化率的敏感性图
4 结论
1)滑坡碎屑流作用下,管道最大椭圆化率随着运行压力的增加而减小,并且伴随滑坡碎屑流厚度的增加,管道最大椭圆化率的减小幅度也随之增大。所以,较大运行压力在一定程度上可以起到增强管道抵抗变形能力的作用。但管道温升对椭圆化率的影响不大。
2)管道径厚比与管道最大椭圆化率成正相关,并且随着滑坡碎屑流厚度增大,管道最大椭圆化率受径厚比的影响越大。随着壁厚减薄加剧,不同规格管道的管道最大椭圆化率随之急剧增加,可见壁厚也是影响管道安全的重要因素,对于埋地管道应注意腐蚀防护,从而减小管道管壁减薄诱发的失效风险。
3)对比滑坡碎屑流厚度、长度、宽度对管道最大椭圆化率影响,宽度影响程度最小,长度次之,厚度的影响最大。
4)在滑坡碎屑流作用条件下,管道最大椭圆化率受运行参数的影响较小,受管道自身结构的影响更大。因此,在天然气管道强度要求条件下,合理设计其结构对增强管道抵抗变形的能力有积极意义。
