中国老年人口死亡模型

梅 丽，王丽娜，姜全保

（西安交通大学 公共政策与管理学院，陕西 西安 710049）

一、引言

随着生育水平的下降和人口预期寿命的延长，中国人口老龄化趋势加剧。《第七次全国人口普查公报》显示2020年中国65岁及以上人口的数量达到1.91亿，比例为13.50%，比2010年的1.19亿增加了7 180万人，提高了4.63个百分点。根据2000年和2010年人口普查数据计算，65岁时老年人口的预期寿命分别为15.25岁和17.53岁。老年人口数量增加、比例上升和预期寿命的延长加深了中国人口老龄化程度。对老年人口死亡水平、死亡模式和预期寿命的研究有助于对人口老龄化水平的理解。

已经有很多学者用数学模型描述和拟合老年阶段的死亡模式。比较经典的包括冈泊茨（Gompertz）模型、［1］冈泊茨-麦克汉姆（Gompertz-Makeham）模型、［2］比尔德（Beard）模型、［3］莰尼斯托（Kannisto）模型，［4］这些模型是逻辑斯蒂（Logistic）模型［5］的特殊情况。还有幂函数形式的威布尔（Weibull）模型［6］和二次方程式（Quadratic）模型［7］等。比尔德尝试使用一种含伽玛（Gamma）分布的个体风险的人口异质性模型解释高龄人口死亡率趋势。［8］近年来，基于极值理论的统计建模方法也开始应用于高龄人口死亡率的研究。［9-12］Watts 等人使用广义帕累托（Generalized pareto）分布和广义极值（Generalized extreme value）分布研究加拿大和日本人口寿命的上尾分布。［9］Li 等人利用极值理论提出了使用门限生命表（Threshold life table）对高龄人口死亡率进行建模分析。［10］段白鸽和孙佳美基于门限生命表方法，使用冈泊茨分布和广义帕累托分布研究了我国高龄人口死亡率变化特征。［11］段白鸽和石磊将高龄人口死亡率的极值建模方法和分层建模技术纳入动态死亡率建模中，度量寿命分布的尾部风险特征。［12］

这些参数模型具有形式简洁、概括性强的优点，但因模型中参数较少，会降低模型的适应范围。例如，冈泊茨模型［1］低估了40 岁以下年轻成年人口死亡率，高估了80 岁及以上老年人口死亡率。［13］麦克汉姆提出在冈泊茨模型的基础上增加一个常数项，该方法改善了年轻成年人口死亡率的拟合，但未解决高龄老年人口死亡率高估的问题。［2］解决冈泊茨模型高估高龄老年人口死亡率问题的一种简单有效的模型是逻辑斯蒂模型。［14-17］Horiuchi 和Wilmoth 建议使用逻辑斯蒂模型来拟合85 岁及以上年龄别人口死亡率。［14］Thatcher 等人使用冈泊茨、威布尔、二次方程式、逻辑斯蒂和莰尼斯托五种模型拟合了13 个国家80-120 岁年龄别人口死亡率，发现莰尼斯托模型拟合效果最好。［15］Zeng 和Vaupel 使用冈泊茨、威布尔、二次方程式、海力戈曼-朴拉德（Heligman-Pollard）、逻辑斯蒂和莰尼斯托六种模型对我国1990年80-96岁年龄别人口死亡率进行了估计，发现莰尼斯托模型对我国高龄人口死亡率的拟合效果比较好。［17］

鉴于已有研究对中国老年人口死亡水平和模式的关注较少，本文尝试使用相关死亡模型，使用MATLAB R2019b 软件实现对65 岁及以上老年人口死亡累计概率的拟合，检验死亡模型的适用性。因此，本文使用不同年份、分城镇乡以及分性别数据，分析并选择出适合老年人口死亡模式的模型，并对死亡最高年龄组进行拓展，以进一步验证模型适用性。希望通过本文分析，能较为准确地选择适合中国老年人口的死亡模型，为相关研究提供方法借鉴。

二、参数模型

目前使用特定模型拟合观测的累计比例在人口学研究中应用广泛。［15］［17-18］本文使用10 种累计概率分布来拟合65岁及以上人口累计死亡概率。把累计死亡概率作为一个累计分布函数（CDF），为了得到累计分布函数，通过人口普查死亡数据中得到年龄别死亡率（mx），然后计算得到年龄别死亡概率，可表示为qx=；以65岁年龄为基点，通过年龄别死亡概率计算得到年龄别存活概率，可表示为；通过年龄别存活概率，进一步计算得到累计死亡概率L65x=1-S65x，以此作为累计分布函数。在模型中，统一使用θ表示尺度参数，κ表示形状参数，μ表示位置参数。模型中设定死亡的起始年龄为sa，文中的年龄数字统一减去起始年龄，从而拟合的曲线是从0 岁开始，但实际描述的是从年龄65 岁开始的情况。具体使用的累计分布函数和公式如下：

指数分布（Exponential distribution）：

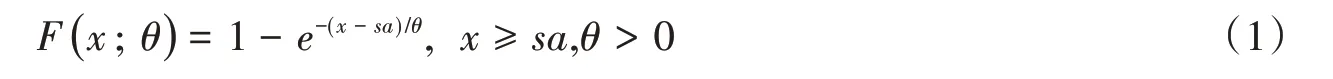
伽玛分布（Gamma distribution）：

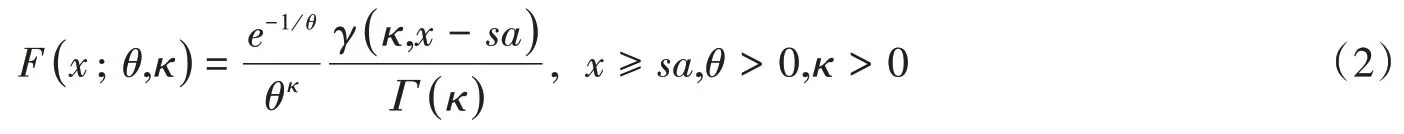
其中，γ(κ,x)是下不完全伽玛函数（The lower incomplete gamma f unction），定义为：

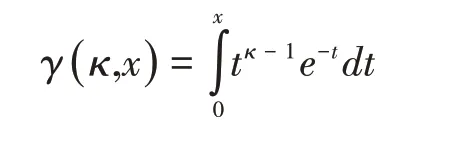
冈泊茨分布（Gompertz distribution）：

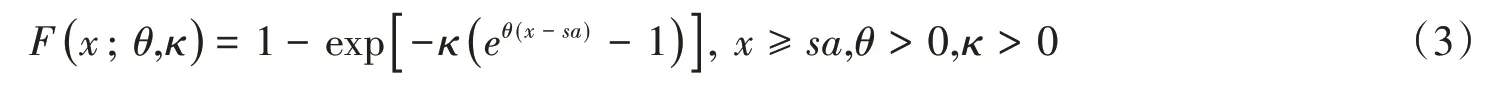
冈泊茨-麦克汉姆分布（Gompertz-Makeham distribution）：

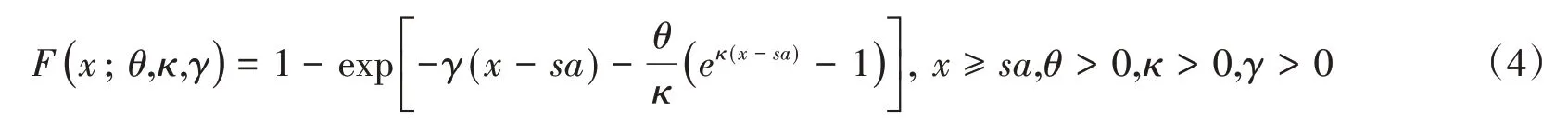
广义极值分布（Generalized extreme value distribution）：

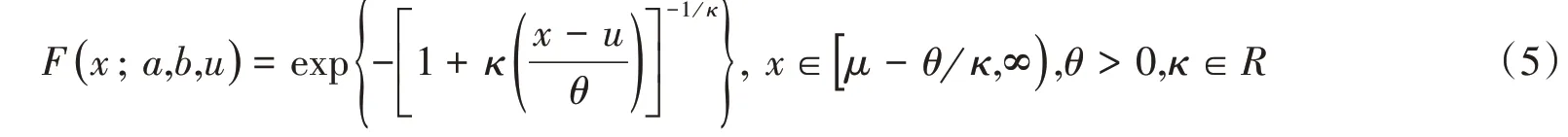
逆高斯分布（Inverse Gaussian distribution）：

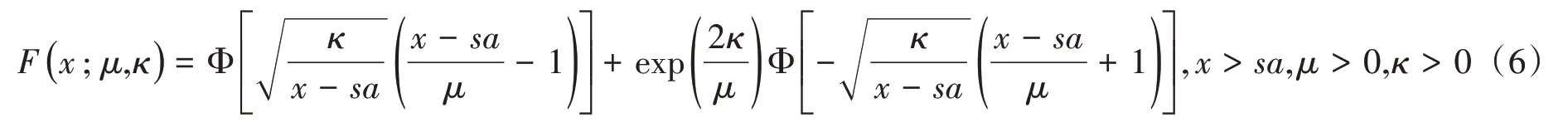
逻辑斯蒂分布（Logistic distribution）：

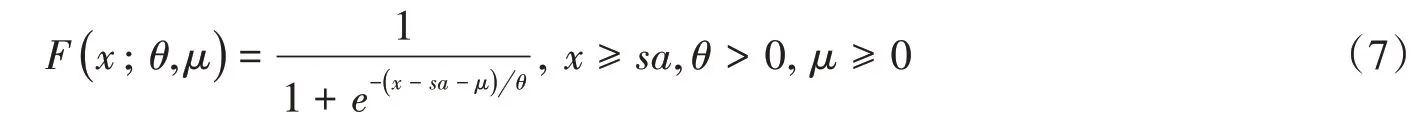
对数-逻辑斯蒂分布（Log-logistic distribution）：

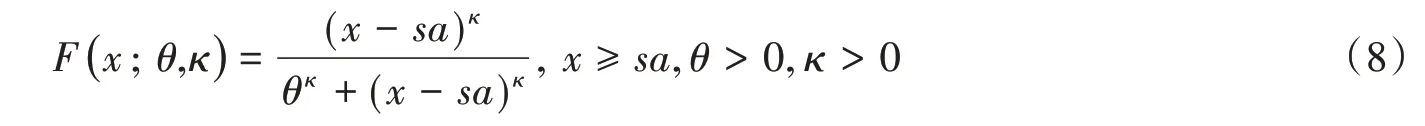
对数-正态分布（Log-normal distribution）：

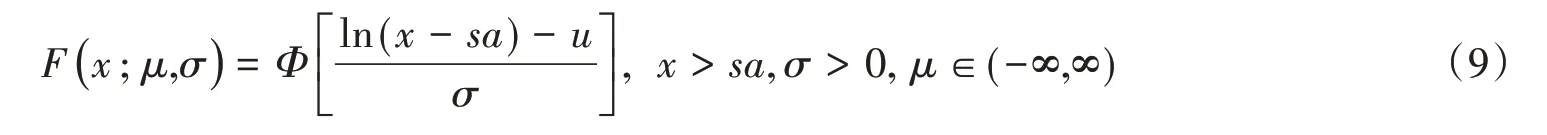
威布尔分布（Weibull distribution）：

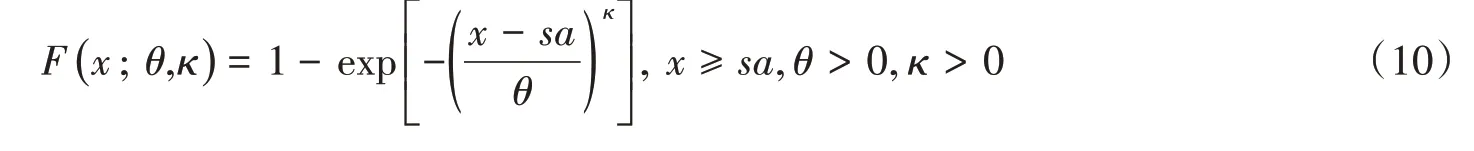
三、数据来源

中国有多个部门登记死亡人口信息。国家卫生健康委员会的人口死亡登记系统（负责开具和收集死亡医学证明信息）、全员人口系统和全国妇幼保健机构监测信息系统；公安部负责户籍登记系统（公民死亡要在户籍系统中注销户口）；民政部的殡葬服务等登记死亡信息数据库；国家统计局的人口普查资料和人口变动情况抽样调查数据也调查死亡人口信息。不同来源的数据由于登记部门不同，目的不同，搜集方法不同，数据之间会存在差异。［19］

国家统计局公布的1982 年、1990 年、2000 年、2010 年四次人口普查资料中老年人口死亡数据漏报程度较轻，但存在老年人口死亡之后不愿申报或者延迟申报等问题。［20-22］许多学者对普查数据进行了修正和调整，李成等使用DCMD 模型生命表系统发现2010 年男性老年人口漏报率男性为2.3%、女性为7.0%。［20］王金营和戈艳霞通过年龄移算方法得出2010 年老年人口的死亡漏报平均在5%以上。［21］崔红艳等使用人口分析技术和与历史数据、行政记录资料比较等方法发现老年人口登记的完整性较高。［22］学者对单独或者分别对某一次或两次普查数据进行研究，或者是使用不同的修正方法，很难有较统一的标准判断人口死亡情况。［21］［23］因此，本文直接使用1982 年、1990 年、2000 年和2010 年全国人口普查资料中65 岁及以上老年人口死亡数据以及2010 年分城镇乡、分性别的死亡数据，计算老年人口死亡率、死亡概率和累计死亡概率等指标，选择累计死亡概率作为累计分布函数，通过lsqcurvefit函数对累计分布函数进行拟合，得到死亡模型拟合结果。

四、拟合结果

1.历次人口普查拟合结果

我们通过MATLAB R2019b 软件拟合1982 年、1990 年、2000 年和2010年65岁及以上老年人口累计死亡概率，得到模型参数和拟合结果的残差平方（SSE）和拟合优度（AdjustedR2）。表1至表4为10 种参数模型对65 岁及以上老年人口累计死亡概率拟合的参数结果。从拟合效果来看，冈泊茨、冈泊茨-麦克汉姆、广义极值、逻辑斯蒂和威布尔五种模型拟合结果中SSE 较小，AdjustedR2更接近于1，拟合效果比较好。而指数模型、伽玛模型的SSE较大，AdjustedR2较小，拟合效果较差。

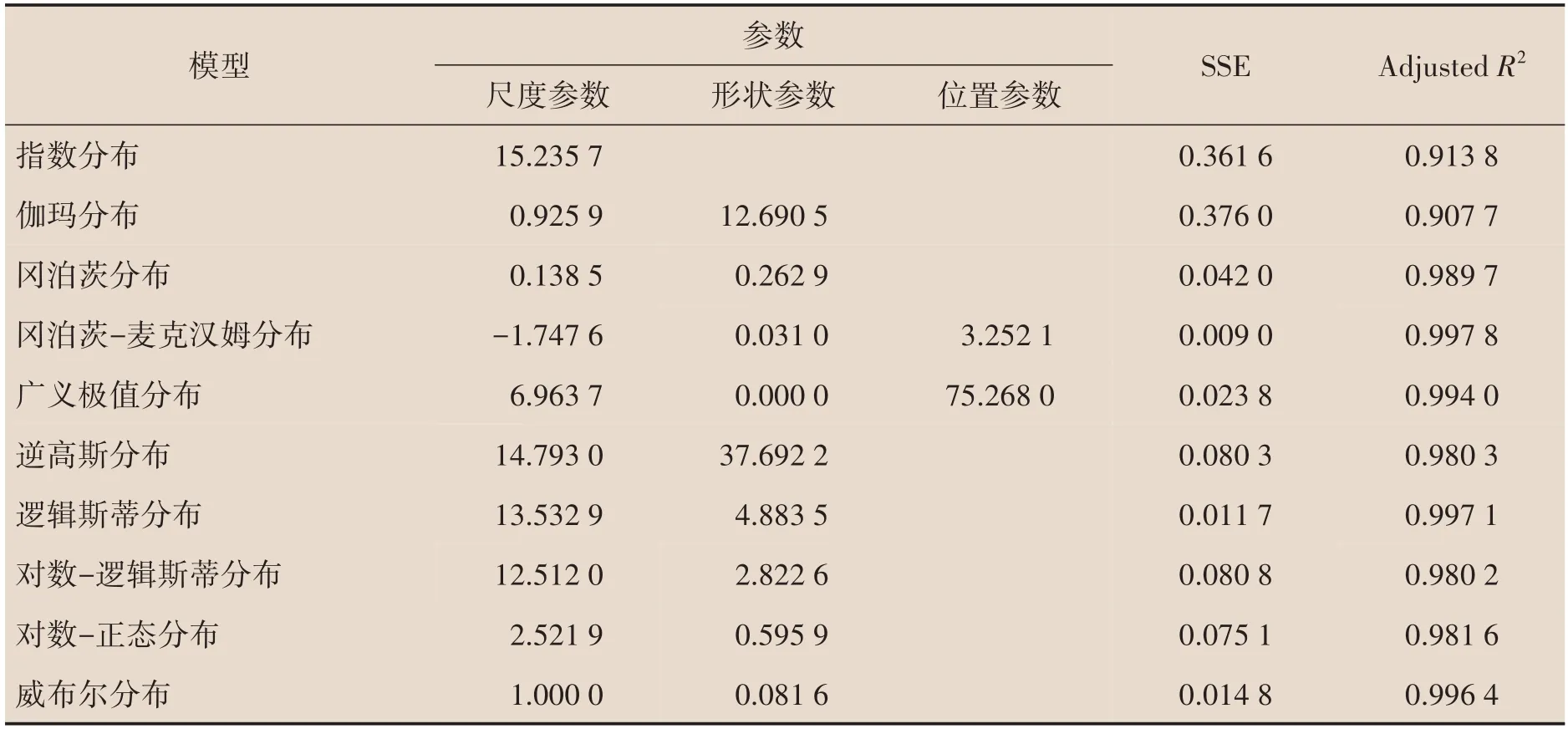
表1 1982年模型参数估计值

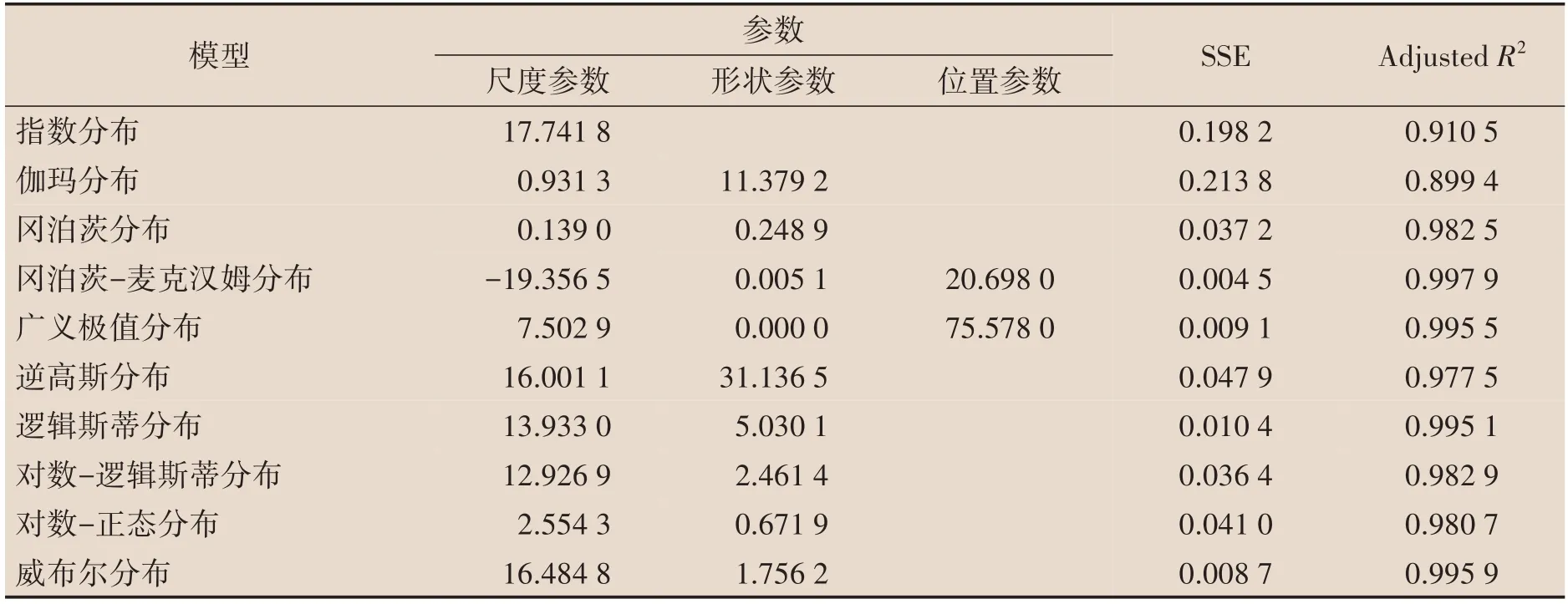
表2 1990年模型参数估计值

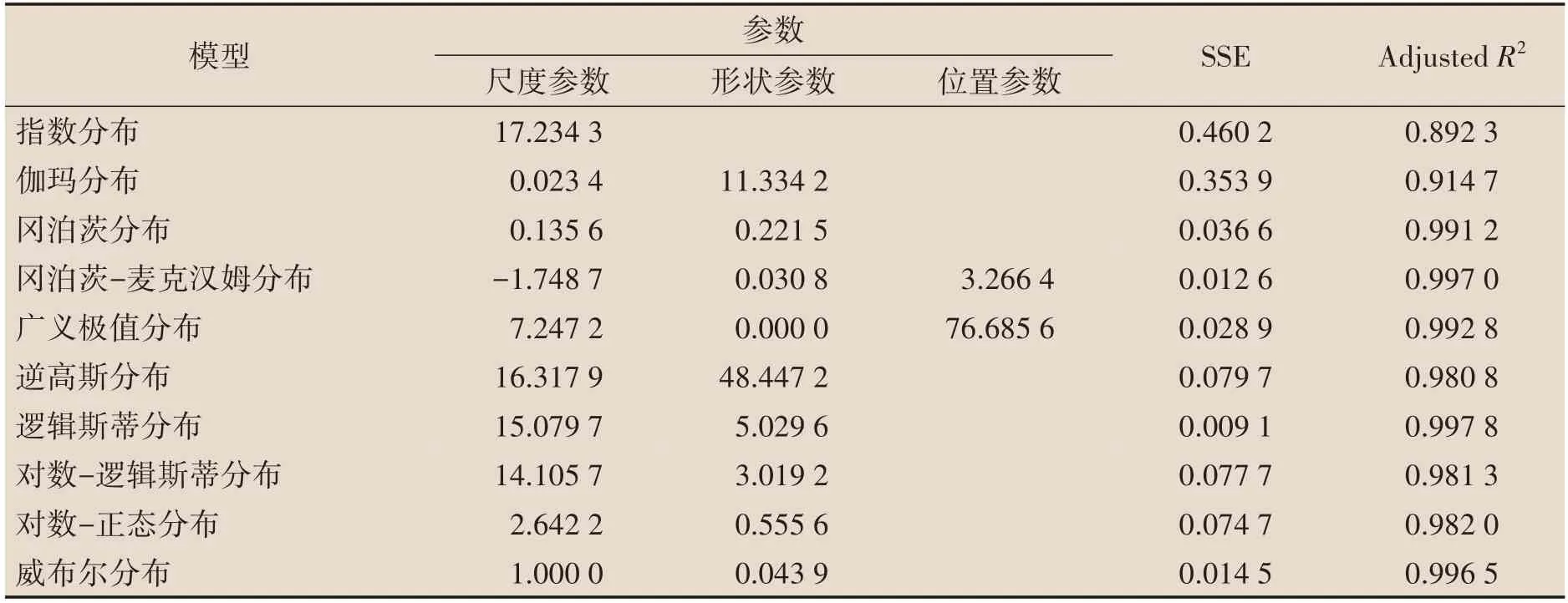
表3 2000年模型参数估计值

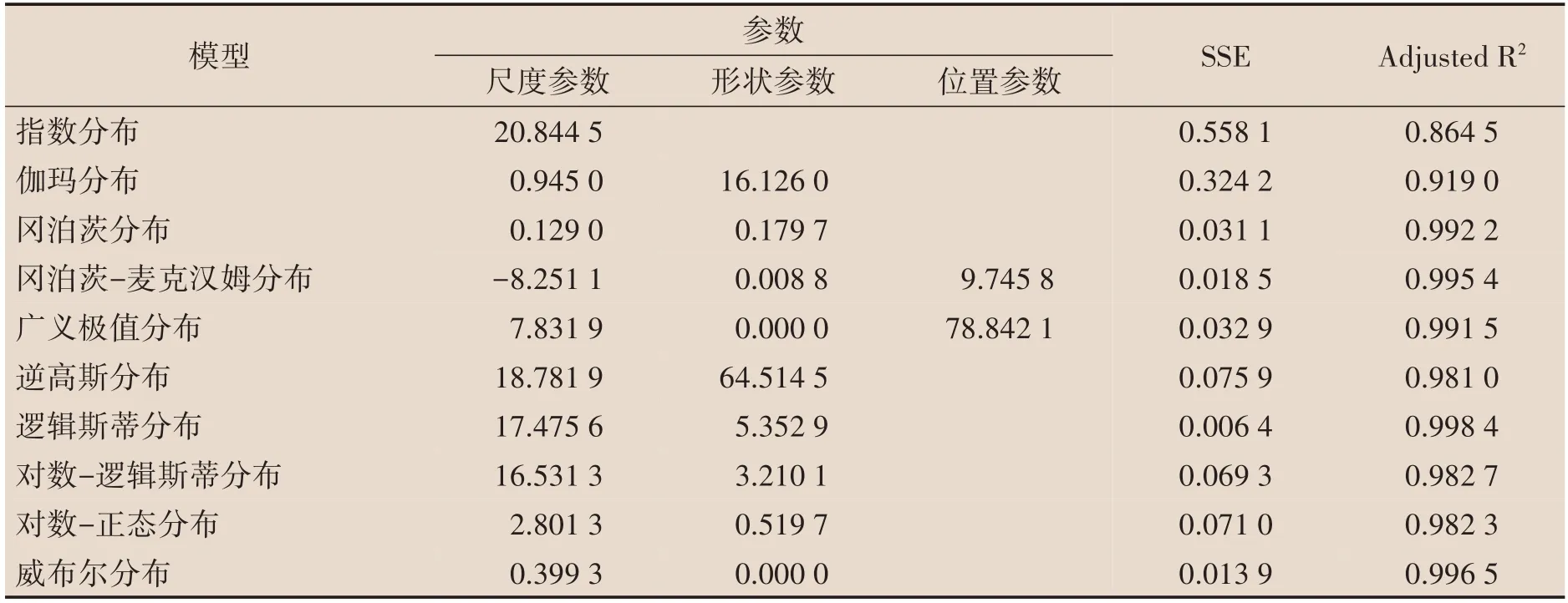
表4 2010年模型参数估计值

通过多种参数模型拟合1982 年、1990 年、2000 年和2010 年四次普查数据老年人口累计死亡概率（见图1）。浅蓝色曲线表示由历次人口普查死亡数据计算得到的累计死亡率概率，称之为观测值；其他颜色表示10 种参数模型的拟合结果，称为拟合值。考虑SSE、AdjustedR2和拟合曲线，1982 年、2000年和2010年三次普查的拟合结果有相同趋势，结果如下：

拟合结果较好的是逻辑斯蒂、冈泊茨-麦克汉姆、威布尔和广义极值四种模型，模型拟合值与观测值之间的差异绝对值较小。逻辑斯蒂模型的拟合值更接近观测值，拟合值和观测值之间差异的绝对值最小，在65-70岁和80-90岁之间拟合值高于观测值，其他年龄的拟合值低于观测值；冈泊茨-麦克汉姆、威布尔和广义极值3 种模型的拟合值与观测值之间的差异值变化一致，大致在65-75 岁和88-100岁之间拟合值低于观测值，76-87岁之间拟合值高于观测值。

拟合结果一般的是冈泊茨、逆高斯、对数-逻辑斯蒂、对数-正态四种模型，模型拟合值和观测值之间差异大于上面模型。逆高斯、对数-逻辑斯蒂、对数-正态三种模型的拟合结果在65-75 岁和87-100 岁之间低于观测值，76-86 岁之间高于观测值；而冈泊茨模型拟合值和观测值之间差异的变化与其他三种模型相反，冈泊茨模型在85 岁之后拟合值高于观测值，例如，1982 年模型拟合结果在95岁时为0.997 9，99岁则达到1。

拟合结果较差的是指数模型和伽玛模型，模型拟合值和观测值之间的差异较大。指数模型的拟合值在65-83 岁之间高于观测值，84-100 岁之间低于观测值；而伽玛分布在65-78 岁和90-100 岁之间的拟合值低于观测值，79-89岁之间的拟合值高于观测值。

相比其他三次人口普查资料中统计的最高死亡年龄是100岁，1990年人口普查资料中最高死亡年龄为90岁，其参数模型拟合结果也发生变化。按照模型拟合值与观测值之间差异大小，1990年参数模型拟合结果的顺序依次是冈泊茨-麦克汉姆模型、威布尔模型、广义极值模型、逻辑斯蒂模型、逆高斯模型、对数-逻辑斯蒂模型、对数-正态模型、冈泊茨模型、指数模型和伽玛模型。

2.分城镇乡拟合结果

使用参数模型对2010年分城镇乡的65岁及以上老年人口累计死亡概率进行拟合（见图2）。

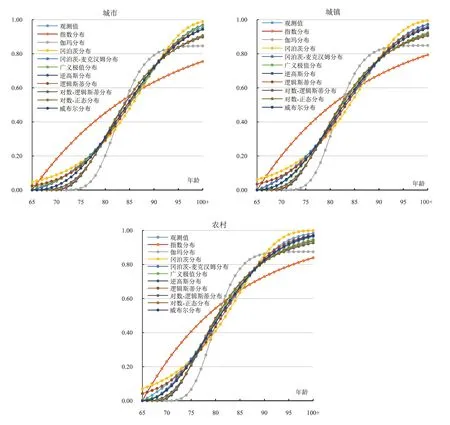
图2 2010年分城乡模型拟合结果

模型拟合结果较好的是冈泊茨-麦克汉姆、广义极值、逻辑斯蒂和威布尔四种模型，模型拟合值与观测值之间差异绝对值较小。冈泊茨-麦克汉姆模型在城市和城镇老年人口的拟合值更接近观测值，在65-75岁和86-95岁之间的拟合值低于观测值，其他年龄的拟合值高于观测值。在农村老年人口中，冈泊茨-麦克汉姆模型与威布尔模型、广义极值模型的拟合值与观测值之间差异变化一致。而在城市和城镇老年人口中，冈泊茨-麦克汉姆、广义极值、逻辑斯蒂和威布尔四种模型拟合值与观测值之间差异的变化趋势均不相同，广义极值模型在65-69 岁、79-88 岁和97-100 岁之间的拟合值均高于观测值；威布尔模型在65-78 岁和91-100 岁之间的拟合值低于观测值，79-90 岁之间的拟合值高于观测值；逻辑斯蒂模型在65-70岁和83-91岁之间的拟合值高于观测值，71-82岁和92-100岁之间的拟合值低于观测值。

模型拟合结果一般的是冈泊茨、逆高斯、对数-逻辑斯蒂和对数-正态四种模型，模型拟合值与观测值之间差异绝对值大于上面模型。逆高斯、对数-逻辑斯蒂和对数-正态三种模型的拟合值与观测值之间差异的变化是一致的，在65-79 岁和91-100 岁之间的拟合值均低于观测值，80-90 岁之间的拟合值均高于观测值；而冈泊茨模型拟合值和观测值之间差异的变化与其他三种模型相反。

模型拟合结果较差的是指数模型和伽玛模型，模型拟合值和观测值之间差异绝对值较大。指数模型的拟合值在65-86 岁之间高于观测值，87-100 岁之间低于观测值。而伽玛模型的拟合结果在65-82岁和94-100岁之间低于观测值，83-93岁之间高于观测值。

3.分性别拟合结果

本文使用模型对2010年分性别的65岁及以上老年人口累计死亡概率进行拟合（见图3）。

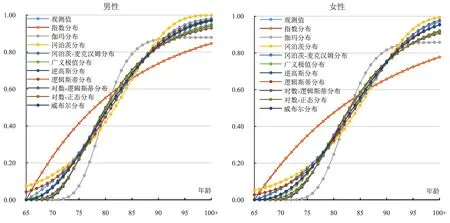
图3 2010年分性别模型拟合结果

拟合结果较好的是冈泊茨-麦克汉姆模型、威布尔模型、逻辑斯蒂模型和广义极值模型，模型拟合值与观测值之间差异绝对值较小。冈泊茨-麦克汉姆模型在女性老年人口的拟合值更接近观测值。同时，在男性老年人口和女姓老年人口中，冈泊茨-麦克汉姆、威布尔和广义极值三种模型的拟合值与观测值之间差异变化一致，在65-75 岁和87-100 岁之间的拟合值低于观测值，其他年龄的拟合值低于观测值；逻辑斯蒂模型在65-70岁和82-91岁之间的拟合值高于观测值，71-81岁和92-100岁之间的拟合值低于观测值。

拟合结果一般的是冈泊茨模型、对数-逻辑斯蒂模型、对数-正态模型和逆高斯模型，模型拟合值与观测值之间差异绝对值大于上面模型。逆高斯、对数-逻辑斯蒂、对数-正态三种模型的拟合结果在65-76岁和89-100岁之间低于观测值，77-88岁之间高于观测值；而冈泊茨模型的拟合结果在65-73岁和87-100岁之间高于观测值，74-86岁之间低于观测值。

模型结果较差的是指数模型和伽玛模型，模型拟合值与观测值之间差异绝对值较大。指数模型的拟合值在65-84岁之间高于观测值，85-100岁之间低于观测值。而伽玛模型的拟合值在65-79岁和91-100岁之间低于观测值，80-90岁之间高于观测值。

4.预测结果

由于中国人口普查的最高年龄组是100 岁，无法知道100 岁之后存活情况。由于联合国模型生命表和寇尔绪曼模型生命表的年龄组拓展到130岁，因此本文将最高年龄组由100岁拓展至130岁。

本文使用2010 年人口普查数据中65 岁及以上累计死亡概率，采用不同模型预测101-130 岁的累计死亡概率，检验10 种模型的拟合效果（见图4）。可以看出指数模型预测的累计死亡概率到130岁达到0.96，即130岁之后超过4%的人口存活，这说明指数模型低估了中国高龄老年人口累计死亡概率。伽玛模型和冈泊茨模型预测值在100 岁之后保持不变，分别为0.86 和1，不符合人口死亡规律。冈泊茨-麦克汉姆、威布尔、逻辑斯蒂、广义极值、逆高斯、对数-逻辑斯蒂和对数-正态七种模型中，逻辑斯蒂模型和威布尔模型，在101 岁的时候达到0.97，之后预测值随着老年人口年龄缓慢上升，接近中国老年人口死亡规律。其他几种模型在100 岁时的累计死亡概率较低，可能低估了死亡水平。

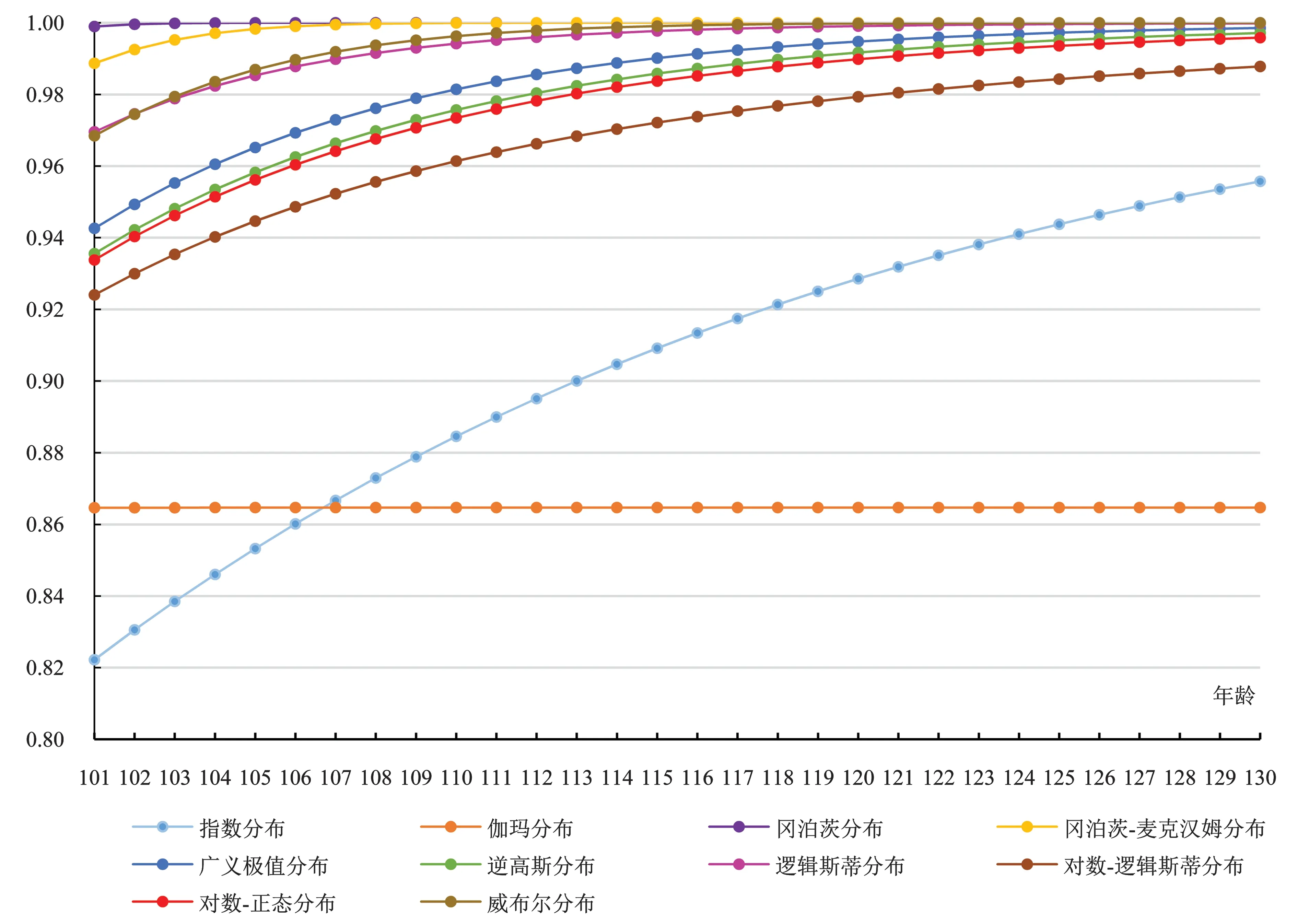
图4 2010年10种模型预测结果

五、结论与讨论

本文使用10种统计模型拟合1982年、1990年、2000年和2010年人口普查中65岁及以上老年人口累计死亡概率，分析了不同模型拟合结果以及模型拟合值与观测值之间的差异，得到结论如下：

从模型拟合结果来看，逻辑斯蒂、冈泊茨-麦克汉姆、威布尔和广义极值四种模型拟合结果较好。已有的研究也表明逻辑斯蒂模型可以较好地拟合老年人口死亡率，［14-15］［17］［24-25］广义极值模型也能很好地反映中国高龄老年人口死亡率曲线，［11-12］冈泊茨-麦克汉姆模型相比冈泊茨模型能更好拟合老年人口死亡模式，但未解决高估高龄老年人口死亡率问题。［2］［13］指数模型和伽玛模型拟合累计分布函数效果较差，不适合拟合老年人口累计死亡概率。

从模型拟合值与观测值之间的差异分析，发现不同模型的拟合值在不同年龄段存在高于或者低于观测值的问题。冈泊茨-麦克汉姆、广义极值、逆高斯、对数-逻辑斯蒂、对数-正态和威布尔六种模型的拟合结果大致在低龄老年阶段和高龄老年阶段低于观测值，在中龄老年阶段高于观测值。冈泊茨模型在低龄老年阶段和高龄老年阶段的拟合值高于观测值，并且拟合值与观测值之间的差异较大。逻辑斯蒂模型的拟合结果与观测值之间的差异值高于冈泊茨-麦克汉姆模型，其差异值在低中高老年阶段呈波动式的变化，能较好地体现中国老年人口死亡模式。［15］［17］2010 年城市、城镇和女性老年人口中，冈泊茨-麦克汉姆模型的拟合值与观测值之间差异的绝对值最小，说明冈泊茨-麦克汉姆模型对城市、城镇和女性死亡数据的拟合结果最好。

使用各种模型将2010年人口普查最高年龄组由100岁拓展到130岁，预测结果发现指数模型和伽玛模型低估了高龄老年人口累计死亡概率，冈泊茨模型高估了高龄老年人口累计死亡概率，逻辑斯蒂和威布尔模型预测结果较好。

本文也存在一定的局限。首先，本文使用不同的模型拟合了老年人口累计死亡概率，虽然可以平滑累计死亡概率曲线，但是不能对死亡数据的漏报做出修正。其次，本文依据时期死亡指标计算得到的累计死亡概率，一定程度上会受到死亡漏报等事件的影响。例如，100岁时老年人口累计死亡概率为0.97，而现实情况中百岁老人的存活率不超过3%。因此，模型拟合结果可能会因为死亡漏报的存在而出现一定偏差。再次，就各种模型来说，针对不同的数据可能有不同的拟合效果，因此，不同的数据需要选择不同的模型。最后，本文使用的是概率分布模型，更多的是认识和应用模型，了解模型的适用性，还需要从更多视角例如分年龄段模型等探讨老年人口死亡模式。