Boundary effects on the sojourn time of two-dimensional inverted inverse quadratic oscillator in a wedge
2022-01-14LeJiayiCHENYinPANXiaoyin
Le Jiayi, CHEN Yin, PAN Xiaoyin
Boundary effects on the sojourn time of two-dimensional inverted inverse quadratic oscillator in a wedge
Le Jiayi, CHEN Yin, PAN Xiaoyin*
( School of physical science and technology, Ningbo University, Ningbo 315211, China )
boundary effect; sojourn time; path-integral; wedge
1 Introduction
Boundary conditions play important roles in almost all areas of classical and quantum physics, including classical electrodynamics[1], quantum field theory[2]and its applications on condensed matter (such as quantum Hall effect[3-6], quantum dots and wires[7-11], graphene[12-14], etc), and fundamental physics like quantum gravity[15]and cosmology[16], as well as in quantum mechanics (QM)[17]. It is well known that the original approach to QM due to Heisenberg and Schrödinger is based on the Hamiltonian formalism, while the Feynman’s path integral method[18-20]is a Lagrangian approach. However, Feynman’s approach becomes more intricate than the Hamiltonian operator approach and requires a sophisticated implementation for systems constrained to bounded domains[21].
The wedge problem, namely the propagation of radiation or particles in the presence of a wedge, as a typical example that shows the significance of boundary condition both in classical and quantum physics has a long history. The earlier work could date back to Sommerfeld’s[22]calculation of diffraction of light by a wedge in 1896. Later, Pauli also studied the wedge problem[23]in the context of diffraction of light.
The quantum version of the wedge problem has been attacked by several groups using path integral techniques independently. Crandall[24]and DeWitt- Morette[25]calculated the propagator for a free particle interacting with a rational wedge. Schulman[26]and Wiegel et al[27]obtain, respectively, the exact propagator of a free particle interacting with a harmonic oscillator, both interacting with an infinite half-plane barrier. Later Cheng[28]generalized their results to the case in the additional presence of a harmonic oscillator potential, the case when the wedge is irrational[29], and further to the case of a two-dimensional inverse quadratic oscillator interacting with a wedge[30].
On the other hand, the calculation of sojourn time which measures the limited time for a particle to sojourn near an unstable equilibrium, is a fundamental problem in quantum mechanics[31-36]. The problem is often idealized drastically and reduces to the behavior of a particle in an inverted harmonic oscillator potential which is exactly solvable and has wide applications in many areas such as evolution of cosmology[37], reactive scattering[38], masers[39], and can serve as a test ground for various approximation methods[40]. Especially, the AB effect on the sojourn time of an inverted two-dimensional (2D) harmonic oscillator under a perpendicular uniform magnetic field has been studied recently[41], and the quantum effect of the integer part of the flux quantum number is manifested for the first time.
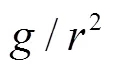
2 The model and evolution of the Gaussian wave packet
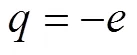
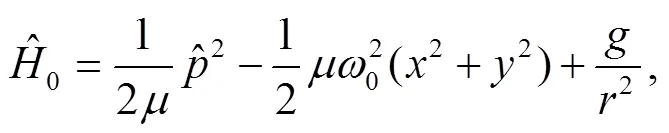
where is the strength of the inverse square potential, . Thus, the particle moves only in the x-y plane with an infinite barrier at angle and , i.e. the wave function must vanish at and . This boundary condition is obviously different from the case in the absence of the wedge, which has a periodic boundary condition . As we shall see below, the change of boundary condition will change the sojourn time dramatically.
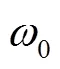
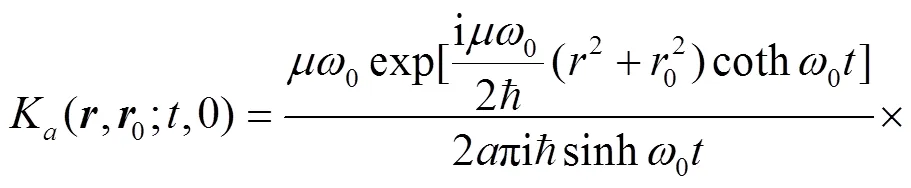
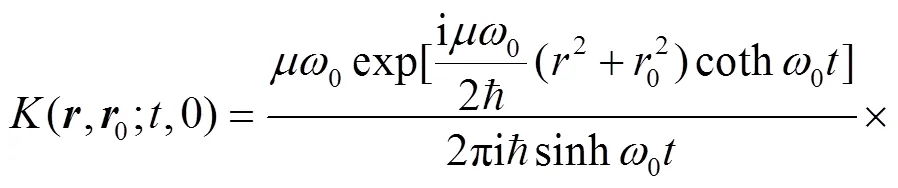
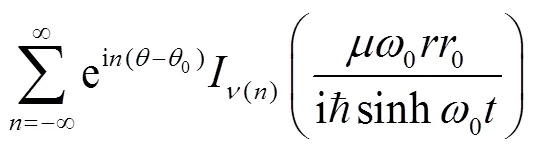
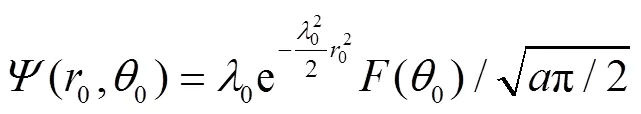
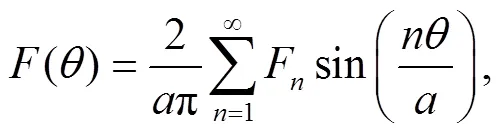
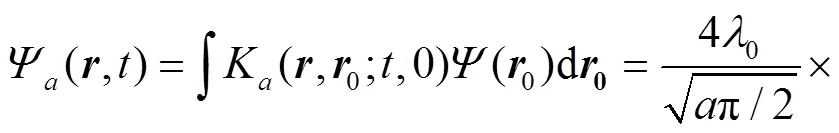
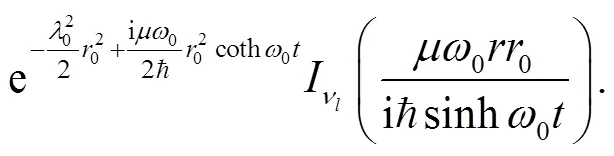
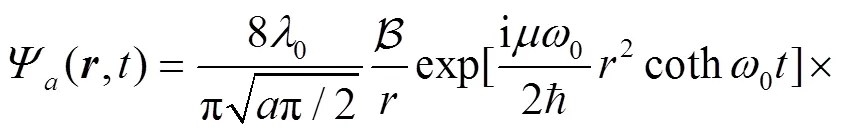
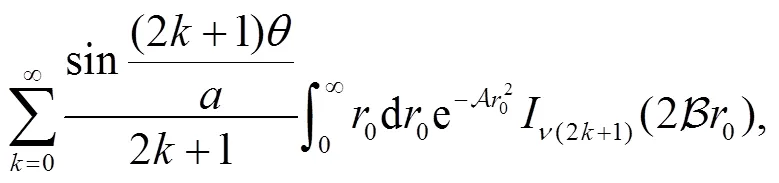
Employ the following identity[43],
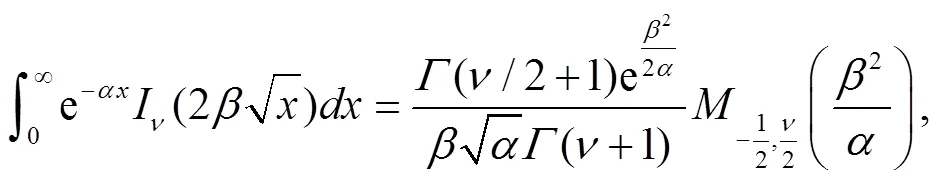
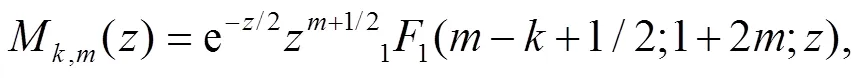
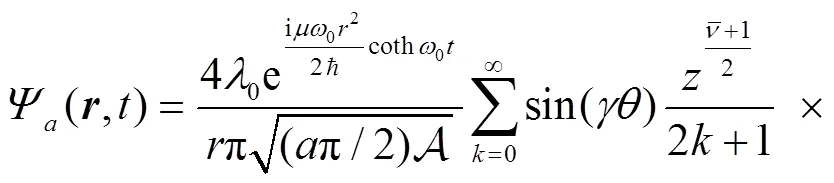
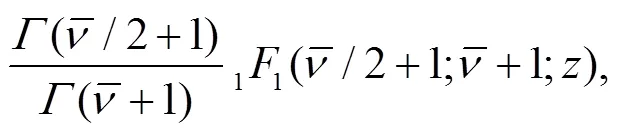
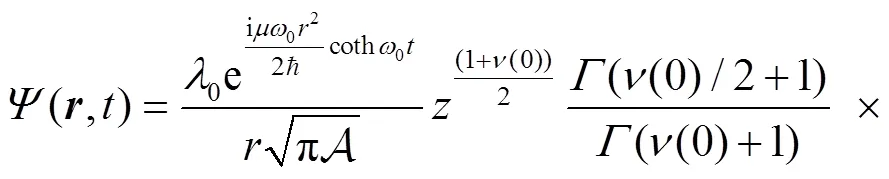
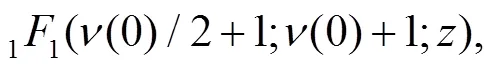
3 Calculation of the sojourn time and numerical results
From the wave function of Eq. (9) we can obtain the corresponding density,
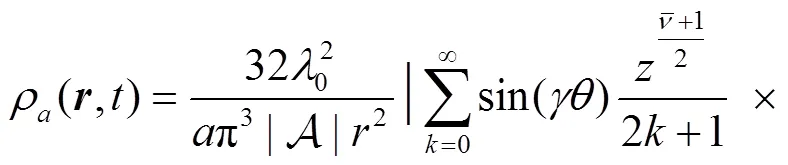
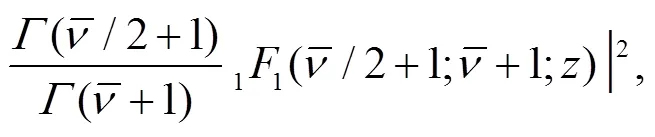
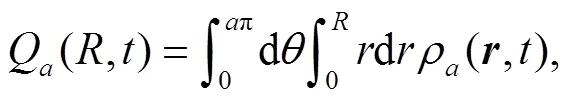
which describes the descent from equilibrium in detail. Substitution of Eq. (12) into Eq. (13) and performing the angle integral yields
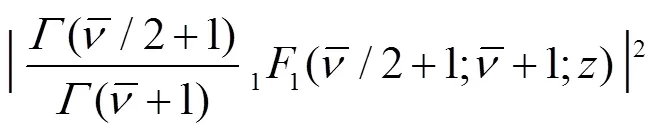
For comparison, we also give the result for the case when the wedge is absent. In this case
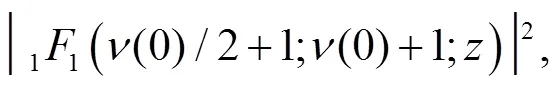
and
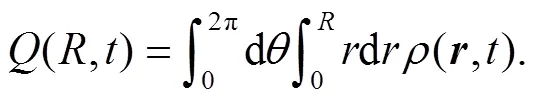
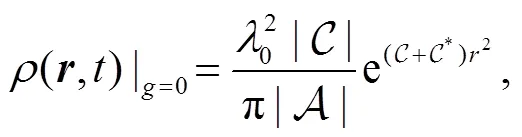
and
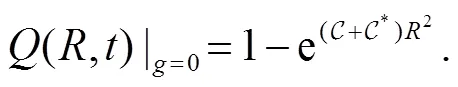
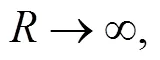
Adopting the definition as that in Ref. [31], we have the expression for the sojourn time,
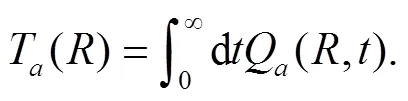
Unfortunately, the integral in Eq. (19) cannot be performed analytically, in order to investigate the effects of the wedge, we have to resort to numerical calculations.
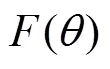
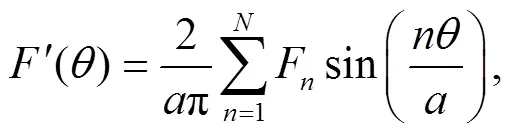
where N is a large integer number. The results for (which is essentially the same as since the difference between the two cases is too small to detect) are presented in Fig. 2. From the graph, it is clear that the sojourn time monotonically increases as the external angle increases as expected. Of particular interest is the case when as shown in Fig. 3. In this case the wedge becomes a singular line and does not occupy any area. It appears that the sojourn time in this case should not differ much from the case without a wedge. However, from the results presented in Fig. 2, it is evident that the sojourn time T has a big jump at (for instance, at , the value of T jumps from 0.3091 to 1.2994, while the value of T jumps from 0.0970 to 0.1500 for , see more in Table 1), implying that there is a huge difference between the case when the wedge becomes a singular line and the one without a wedge. In other words, a singular line which does not occupy any area in 2D space, but counter- intuitively can reduce the sojourn time dramatically to about or more than 30 percentage less. Namely, the time for the particle to stay in the circle with radius is reduced to less than 70 percentage of the original value when the circle is cut by a singular line. Particularly, the sojourn time is reduced to about 24 percentage of the value of in the case when . This surprising huge amount of difference indicates that the boundary indeed plays an important role in this problem.
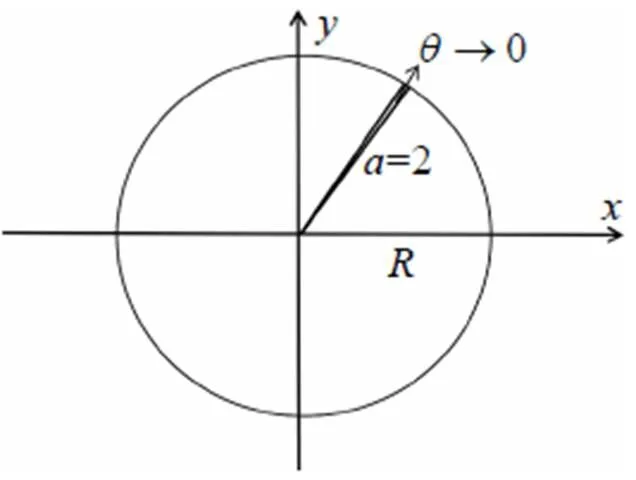
Fig. 3 The wedge in the limit of
Table 1 The values of the sojourn T (R=1) at and for different values ofg
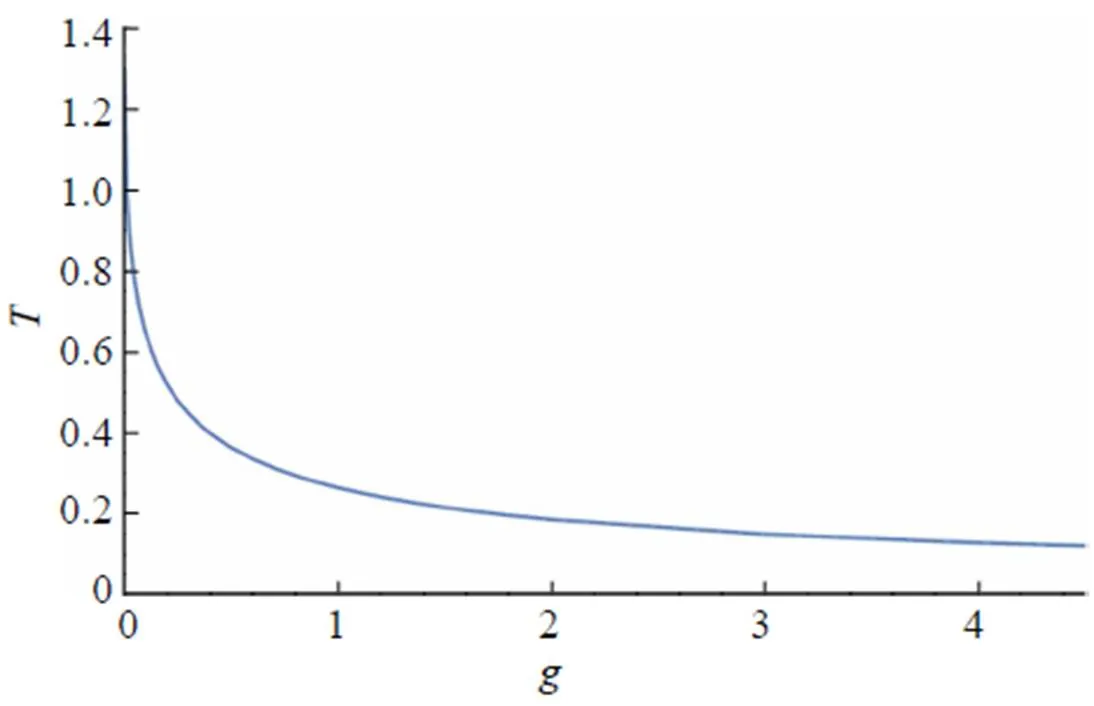
Fig. 4 Sojourn time as a function of g at in the absence of the wedge ()
4 Discussions and concluding remarks
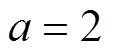
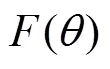
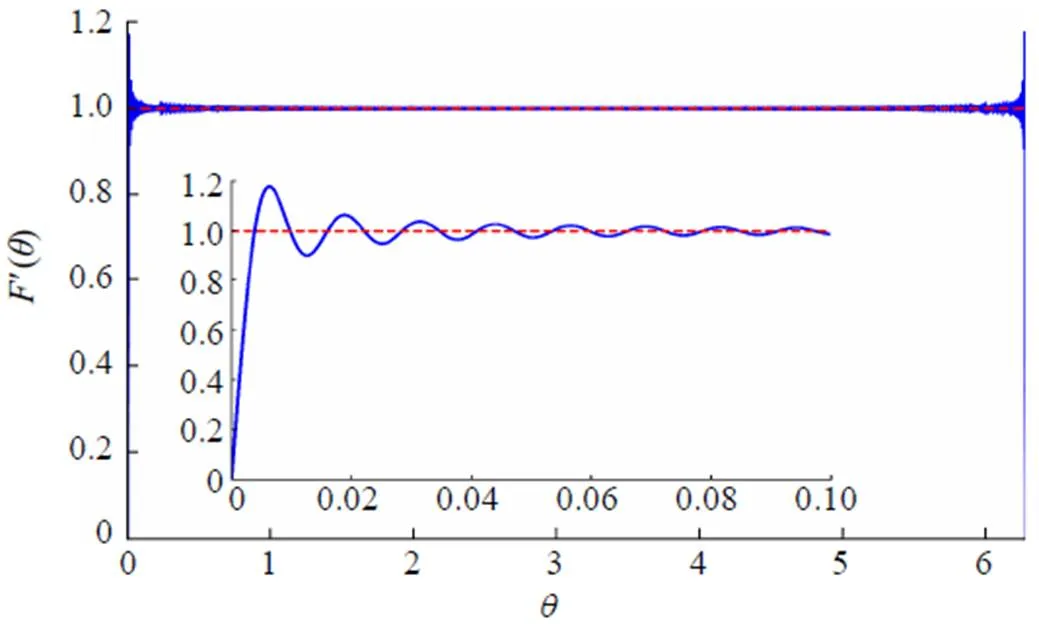
Fig. 5 The plot of function for ,
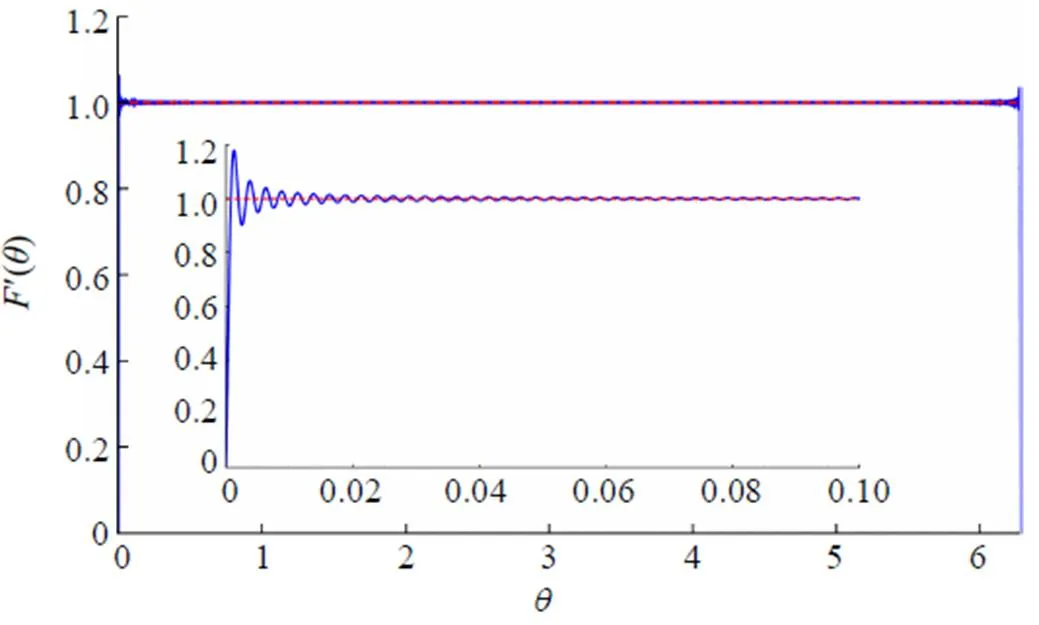
Fig. 6 The plot of function for ,
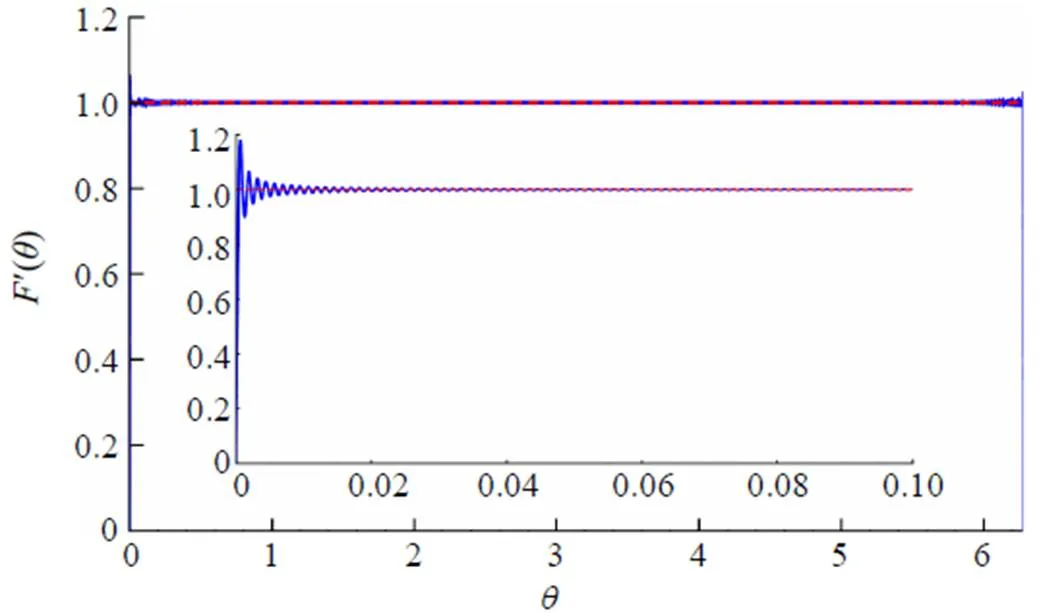
Fig. 7 The plot of function for ,
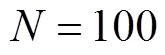
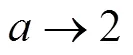
[1] Jackson J D. Classical Electrodynamics[M]. 3rd ed. Zurich: Wiley-VCH, 1998:832.
[2] Glimm J, Jaffe A. Quantum Physics—A Functional Integral Point of View[M]. Berlin: Springer-Verlag, 1987.
[3] Klitzing K V, Dorda G, Pepper M. New method for high-accuracy determination of the fine-structure constant based on quantized Hall resistance[J]. Physical Review Letters, 1980, 45(6):494-497.
[4] MacDonald A H. Quantum Hall Effect: A Perspective[M]. Dordrecht: Springer Netherlands, 1989.
[5] Chakraborty T, Pietiläinen P. The Fractional Quantum Hall Effect[M]. Heidelberg: Springer-Verlag, 1988.
[6] Prange R E, Girvin S M. The Quantum Hall Effect[M]. New York: Springer, 1990.
[7] Chakraborty T. Quantum Dots[M]. Amsterdam: Elsevier, 1999.
[8] Jacak L, Harylak P, Wojs A. Quantum Dots[M]. Heidelberg: Springer-Verlag, 2013.
[9] Reimann S M, Manninen M. Electronic structure of quantum dots[J]. Reviews of Modern Physics, 2002, 74(4):1283-1342.
[10] Hanson R, Kouwenhoven L P, Petta J R, et al. Spins in few-electron quantum dots[J]. Reviews of Modern Physics, 2007, 79(4):1217-1265.
[11] Harrison P, Valavanis A. Quantum Wells, Wires and Dots: Theoretical and Computational Physics of Semiconductor Nanostructures[M]. 4th ed. Hoboben, NJ: John Wiley & Sons, 2016:505-542.
[12] Novoselov K S, McCann E, Morozov S V, et al. Unconventional quantum Hall effect and Berry’s phase of 2π in bilayer graphene[J]. Nature Physics, 2006, 2(3): 177-180.
[13] Castro Neto A H, Guinea F, Peres N M R, et al. The electronic properties of graphene[J]. Reviews of Modern Physics, 2009, 81(1):109-162.
[14] Kotov V N, Uchoa B, Pereira V M, et al. Electron- electron interactions in graphene: Current status and perspectives[J]. Reviews of Modern Physics, 2012, 84(3): 1067-1125.
[15] Birrell N D, Davies P C W. Quantum Fields in Curved Space[M]. Cambridge: Cambridge University Press, 1984.
[16] Preskill J. Cosmic strings and other topological defects[J]. Science, 1996, 272(5264):966-971.
[17] Grosche C.-Function perturbations and boundary problems by path integration[J]. Annalen der Physik, 1993, 505(6):557-589.
[18] Müller-Kirsten H J W. Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral[M]. Singapore: World Scientific Publishing, 2006.
[19] Feynman R P, Hibbs A R. Quantum Mechanics and Path Integrals[M]. New York: McGraw-Hill, 1965.
[20] Feynman R P. Space-time approach to non-relativistic quantum mechanics[J]. Reviews of Modern Physics, 1948, 20(2):367-387.
[21] Asorey M, Clemente-Gallardo J, Muñoz-Castañeda J M. Boundary conditions: The path integral approach[J]. Journal of Physics: Conference Series, 2007, 87:012004.
[22] von Sommerfeld A. Über verzweigte potentiale im raum [J]. Proceedings of the London Mathematical Society, 1896, 28(1):395-429.
[23] Pauli W. On asymptotic series for functions in the theory of diffraction of light[J]. Physical Review, 1938, 54(11): 924-931.
[24] Crandall R E. Combinatorial approach to Feynman path integration[J]. Journal of Physics A: General Physics, 1993, 26(14):3627-3648.
[25] DeWitt-Morette C. Feynman path integrals: I. Linear and affine techniques; II. The Feynman-Green function[J]. Communications in Mathematical Physics, 1974, 37(1): 63-81.
[26] Schulman L S. Exact time-dependent Green’s function for the half-plane barrier[J]. Physical Review Letters, 1982, 49(9):599-601.
[27] Wiegel F W, Michels J J. Dynamics of unwinding of a simple entanglement[J]. Journal of Physics A: General Physics, 1987, 20(14):4653-4659.
[28] Cheng B K. The two-dimensional harmonic oscillator interacting with a wedge[J]. Journal of Physics A: General Physics, 1990, 23(24):5807-5814.
[29] Inomata A. Remarks on the Time Transformation Technique for Path Integration[M]//Gutzwiller M C, Inomata A, Klauder J R, et al. Path Integrals from meV to MeV. Singapore: World Scientific Publishing, 1986:433-448.
[30] Cheng B K, Luz M E. Exact propagator for a two- dimensional inverse quadratic oscillator interacting with a wedge[J]. Journal of Physics A: General Physics, 1992, 25(7):2033-2042.
[31] Barton G. Quantum mechanics of the inverted oscillator potential[J]. Annals of Physics, 1986, 166(2):322-363.
[32] Baskoutas S, Jannussis A, Mignani R. Study of the generalized parametric oscillator[J]. Physics Letters A, 1992, 164(1):17-22.
[33] Baskoutas S, Jannussis A, Mignani R. Quantum tunnelling of a damped and driven, inverted harmonic oscillator[J]. Journal of Physics A: General Physics, 1993, 26(23):7137-7147.
[34] Guo G J, Ren Z Z, Ju G X, et al. Quantum tunneling effect of a time-dependent inverted harmonic oscillator[J]. Journal of Physics A: Mathematical and Theoretical, 2011, 44(18):185301.
[35] Guo G J, Ren Z Z, Ju G X, et al. Quantum tunneling effect of a driven inverted harmonic oscillator[J]. Journal of Physics A: Mathematical and Theoretical, 2011, 44(30): 305301.
[36] Guo G J, Ren Z Z, Ju G X, et al. The sojourn time of the inverted harmonic oscillator on the noncommutative plane[J]. Journal of Physics A: Mathematical and Theoretical, 2011, 44(4):425301.
[37] Felder G, Frolov A, Kofman L, et al. Cosmology with negative potentials[J]. Physical Review D, 2002, 66(2): 023507.
[38] AbuSalbi N, Kouri D J, Shima Y, et al. Quantum mechanical study of the D+H2→HD+H reaction[J]. The Journal of Chemical Physics, 1985, 82(6):2650-2661.
[39] Fahyan S E. Laser physics[D]. Malang, Indonesia: Universitas Negeri Malang, 1993.
[40] Bender C M, Cooper F, Milton K A, et al. Discrete-time quantum mechanics. III. Spin systems[J]. Physical Review D, 1987, 35(10):3081-3091.
[41] Wang Y J, Guo W, Pan X Y, et al. The Aharonov-Bohm effect on the sojourn time of the two-dimensional inverted harmonic oscillator under a perpendicular magnetic field[J]. Europhysics Letters, 2019, 124(6):60007.
[42] Bogachek E N, Landman U. Edge states, Aharonov- Bohm oscillations, and thermodynamic and spectral properties in a two-dimensional electron gas with an antidot[J]. Physical Review B, 1995, 52(19):14067-14077.
[43] Gradshteyn I S, Ryzhik I M, Jeffrey A, et al. Table of integrals, series, and products[J]. Journal of Biomechanical Engineering, 1981, 103(1):58.
[44] Wang Z, Guo D. An Introduction to Special Function[M]. Beijing: Peking University Press, 2000. (in Chinese)
边界对二维反谐振子在平方反比势和楔子中逗留时间的影响
乐家怡, 陈 寅, 潘孝胤*
(宁波大学 物理科学与技术学院, 浙江 宁波 315211)
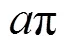
边界效应; 逗留时间; 路径积分; 楔子
2021−10−08.
宁波大学学报(理工版)网址: http://journallg.nbu.edu.cn/
国家自然科学基金(11375090).
乐家怡(1996-), 女, 浙江慈溪人, 在读硕士研究生, 主要研究方向: 量子力学. E-mail: 592981258@qq.com
潘孝胤(1974-), 男, 浙江宁海人, 研究员, 主要研究方向: 凝聚态理论. E-mail: panxiaoyin@nbu.edu.cn
O413.1
A
1001-5132(2022)01-0105-07
(责任编辑 韩 超)
