变截面格构式结构轴压临界力的高效分析方法
2022-01-13孟丽霞于傲群刘士明
孟丽霞,于傲群,刘士明
(沈阳建筑大学机械工程学院,辽宁 沈阳 110168)
1 引言
由众多梁杆组成的复杂格构式结构,广泛应用于建筑钢结构、起重机械臂架、输电塔架以及某些桥梁结构中,其中变截面格构式结构凭借自重轻、材料利用合理、容易实现等强度原则,在工程实际中应用更加广泛。结构的轴压稳定性问题明显区别强度问题,结构失稳破坏由于事发前没有明显的征兆,一旦失稳破坏即会对人身安全、社会经济造成不可逆的损害。因此,许多学者将结构的稳定性分析作为关注的焦点。现阶段,采用有限单元法、静力法等分析等截面实腹式构件以及简单组合结构的轴压稳定性问题已相对成熟[1-3]。而相较于等截面梁单元研究,目前变截面梁单元的传统做法是将其密分成多段等截面梁单元进行模拟,这种方法已经被证明是相当低效的。文献[4]利用数值计算求解出一种具有轴向力和剪切变形的梁单元精确刚度矩阵。文献[5]利用有限差分法对变截面悬臂梁单元进行了计算分析。文献[6]基于Euler-Bernoulli梁理论研究了具有不同截面形状的变截面梁单元沿长度的惯性矩变换,然后采用Bessel函数,获得了包括轴向力影响的刚度矩阵。文献[7]将变截面构件载荷转换为等效节点载荷,采用增量割线刚度方法,推导出工程中常见截面类型统一表述的新型变截面梁单元。
文献[8]提出一种TTH弯曲梁柱单元,并计入二阶效应影响对变截面工字梁单元进行研究。针对复杂格构式结构或桁架结构的稳定性分析,目前主要采用有限单元法,一个结构进行一次建模,建模工作量大,计算效率不高。为了提高计算准确率和效率,许多学者对格构式结构的稳定性和非线性变形进行了深入的研究[9-13]。其中,在等截面格构式结构研究方面,学者们采用共旋坐标法、弧长法等对其进行了研究[9-10]。在变截面格构式结构研究方面,Theodore G.假设变形曲线,采用加辽金法获得含有锥形截面的多跨梁与框架结构的失稳临界力[11]。文献[12]通过惯性矩等效方式将臂架从格构式结构简化为实腹式梁结构进行稳定性研究。文献[13]利用多项式函数进行变截面梁单元的高阶计算,采用五次Hermit插值获得形函数,刚度矩阵具有较精确的表达形式,但其获得的变截面梁单元光滑连续性不高,并且插值函数阶数过高会导致收敛性较差,最终使得求解精确度降低。
使用三次样条函数构建变截面格构式梁单元位移场,基于非线性有限元法推导计及二阶效应的变截面格构式梁单元的切线刚度矩阵,结合静力凝聚法获得一种新型的两节点梁单元,利用该单元对由梁杆组成的变截面格构式结构的轴压稳定性进行分析。
2 三次样条变截面梁单元位移场
变截面格构式梁单元,如图1所示。单元长度为l,在任意截面x处的截面惯性矩I(x)、面积A(x)与原点o处的截面惯性矩I0、面积A0的关系为:

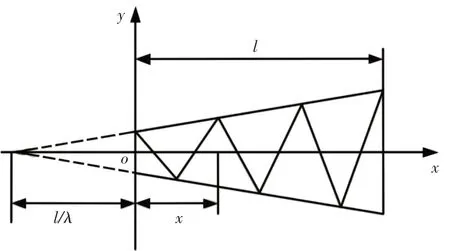
图1 变截面格构式梁单元Fig.1 The Lattice Beam Element with Variable Section
利用三次样条插值推导变截面梁单元切线刚度阵时,对梁单元进行基本假定:
(1)梁单元变形时,单元横截面与变形前保持一致;
(2)遵循广义Hooke定律,单元材料为各向同性;
(3)梁单元横截面在变形后仍垂直于法线。
通过以上假定得到函数形式:

式中:λ—变截面构件锥度的无量纲参数,λ>-1。
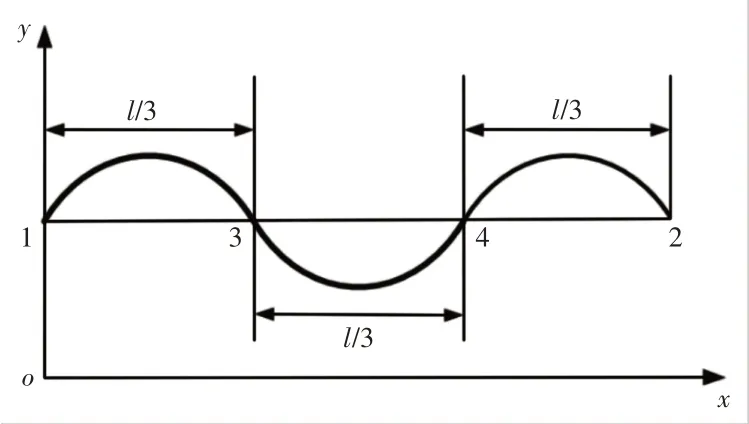
图2 三次样条变截面格构式梁单元描述Fig.2 Cubic Spline Description of Variable Section Lattice Beam Element

根据三次样条插值定理,由于梁单元样条曲线等分为3份,每份样条曲线的横向位移场均可表示为三次多项式,并且多项式参数是由节点的边界条件和单元变形的连续条件决定的,如下所示。

式中:ξ=x/l。结合上述条件,获得变截面格构式梁单元的横向位移场形函数向量:


式(6)两侧同时对y取积分得:


3 变截面梁单元切线刚度矩阵
在大位移大转角小应变条件下,忽略格林应变中与纵向位移相关的高阶项得:

其中各变量的具体表达式详见附录。当刚度矩阵式(17)中锥度系数λ→0且轴力P→0时,所得的变截面梁单元刚度矩阵KT即可转化成传统等截面梁单元刚度矩阵K′T:

4 算例分析

选取无量纲稳定系数mcr=pcrl2/(EI2),分析该悬臂变截面格构式构件的整体稳定性。采用本文新型变截面格构式梁单元,将构件划分为一个单元,得到对应刚度矩阵:

由结构失稳临界力方程Det[KT]=0,获得轴压失稳临界力,进而可得稳定系数mcr,并与文献[14]的理论精确解进行对比,对比结果,如表1所示。
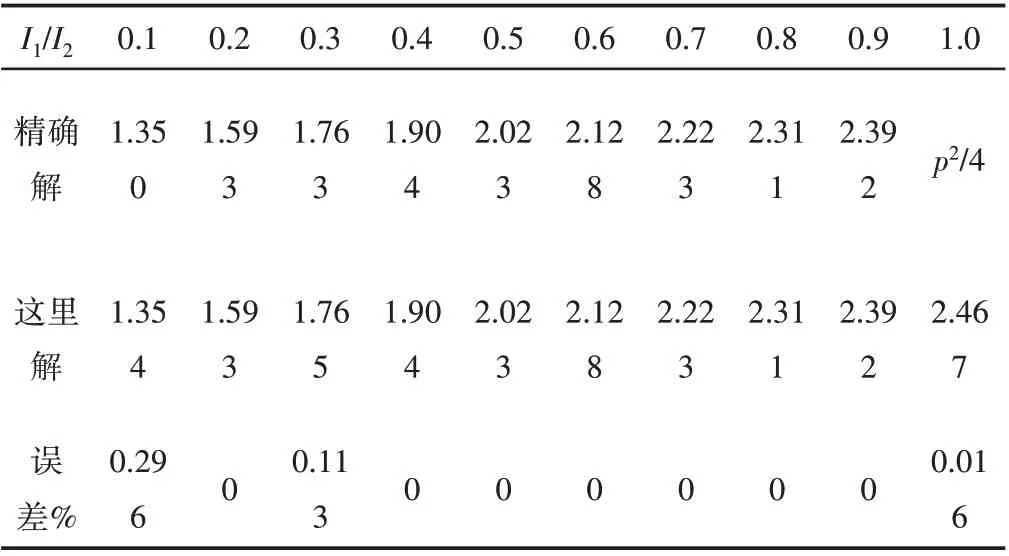
表1 悬臂格构式构件稳定系数mcr计算比较Tab.1 Comparison of Stability Coefficients mcr of Cantilever Lattice Structure
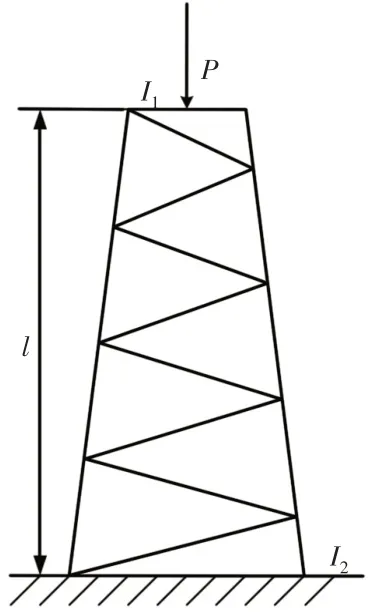
图3 悬臂变截面格构式构件Fig.3 Cantilever Variable Section Lattice Structure

将该组合构件中每个变截面段划分为一个单元,其中变截面单元1和3利用这里获得的新型梁单元刚度阵进行计算,等截面单元2利用这里刚度阵令λ=0退化得到的等截面梁单元刚度阵进行计算。通过刚度矩阵组装集成求解可得到该梭形构件的失稳临界力。计算出不同I1/I2和x/l情况下的mcr值,这里结果与文[14]理论结果对比,如表2所示。

图4 简支梭形格构式组合构件Fig.4 The Combined Spindle Lattice Structure with Simple Support
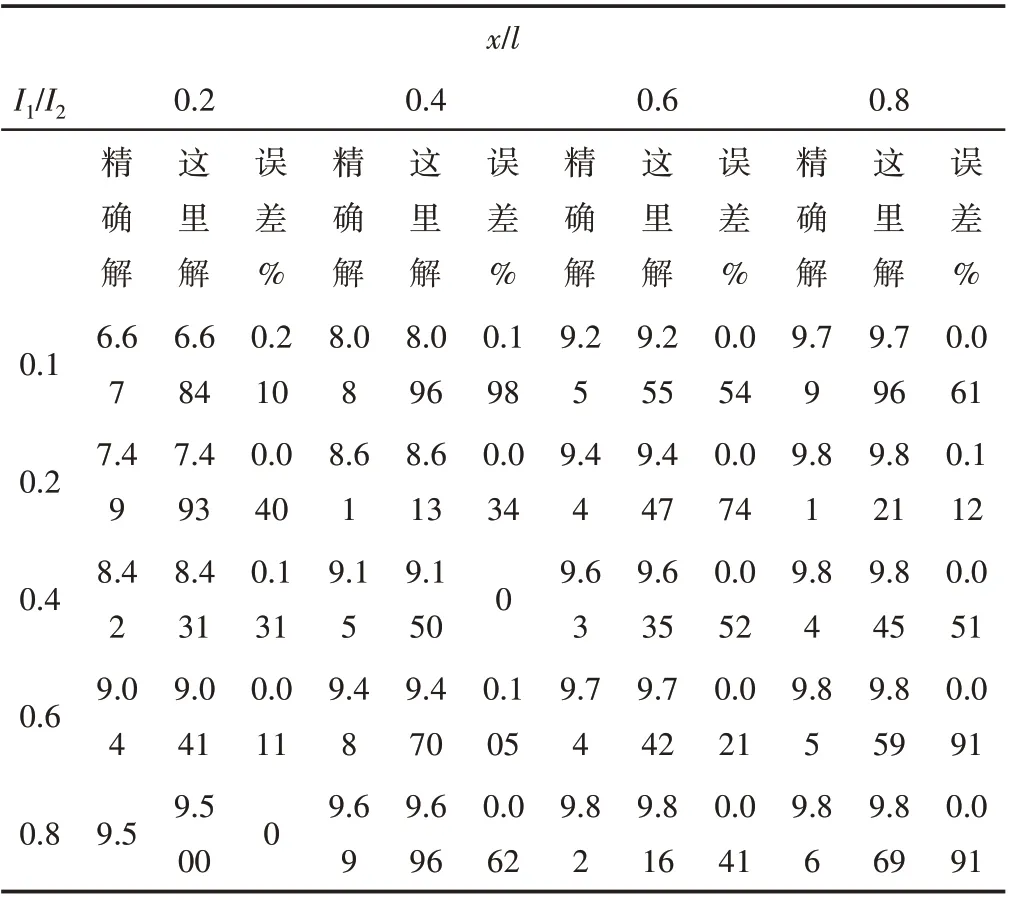
表2 梭形格构式构件稳定系数mcr计算比较Tab.2 Comparison of the Stability Coefficient mcr of the Combined Spindle Lattice Structure
由表1、表2结果可见,这里所推导的变截面格构式梁单元切线刚度矩阵在进行结构的稳定性分析时,具有非常高的计算精度。本文获得的新型梁单元不仅可用于单构件轴压稳定性分析,也可用于变截面、等截面组合构件的轴压稳定性分析。同时,所形成的整体刚度阵与传统两节点梁单元具有相同的阶数,可以方便实现变截面梁到等截面梁的转化。
5 结论
(1)基于有限元插值理论,采用三次样条插值推导变截面格构式梁单元的切线刚度矩阵,随后结合静力凝聚法消除单元节点的曲率自由度,推导出一种新型的变截面格构式梁单元;(2)利用推导的变截面格构式梁单元刚度矩阵对变截面格构式悬臂结构和简支梭形格构式组合结构进行轴压稳定性分析,计算结果与Timoshenko精确解几近相同,表明这里方法可高效地分析由梁杆组成的复杂变截面格构式结构的稳定性问题;(3)这里凝聚后的变截面梁单元刚度阵与传统有限元法所得梁单元刚度阵的阶数保持一致,可与传统梁单元刚度阵集成组装,方便统一分析求解;且当λ趋于0时,这里刚度阵可退化为计及二阶效应的等截面梁单元刚度阵。
附录:

