旋压皮带轮疲劳安全因子的研究
2022-01-13翁剑成
翁剑成
(龙岩学院物理与机电工程学院,福建 龙岩 364000)
1 引言
皮带轮是机械设备中重要的传动部件,在传动动力和运动工作过程中,承受着交变载荷作用,在应力集中位置容易产生微裂纹,在疲劳载荷持续作用下,微裂纹会扩展成宏观裂纹,最后导致皮带轮断裂失效。
为了避免旋压皮带轮工作过程中发生疲劳断裂失效,生产前需要设计其疲劳强度,使其工作承受的交变应力小于材料的疲劳极限[1]。
目前,对旋压皮带轮进行疲劳实验主要是把皮带轮悬挂起来进行旋转,一直转到出现微裂纹为止。
为了避免疲劳试验耗人时,耗材力和周期长等缺点,伴随计算机硬件技术的飞速发展和有限元软件功能的不断强大,有限元数值模拟方法在旋压皮带轮设计中的应用越来越广泛,相应地获得了一系列研究成果,而纵观这些有关旋压皮带轮的数值模拟研究成果中[2-4],不难发现有关皮带轮成型工艺模拟及设计方面的研究文献居多[5-7],而旋压皮带轮疲劳寿命的相关研究文献较少。
在疲劳寿命研究中,主要是基于修正的材料应变-寿命曲线进行评估[8-9],材料应变-寿命曲线主要通过实验获取,耗时长,成本高。
这里以某公司生产的皮带轮为研究对象,应用极限应力图是对其疲劳安全工作范围进行控制,并借助有限元计算结果计算其疲劳安全因子,为皮带轮安全工作提供科学手段。
2 极限应力图及疲劳安全因子计算理论
在工作过程中,零部件往往不是受到单一应力循环特性而是承受着不同循环特性,根据文献[10]可知不同循环特性下,结构的疲劳极限不同,它们之间的相互关系可以通过极限应力曲线图进行描述。
结构受到的应力幅σa随结构承受的平均应力σm变化关系,如图1所示。
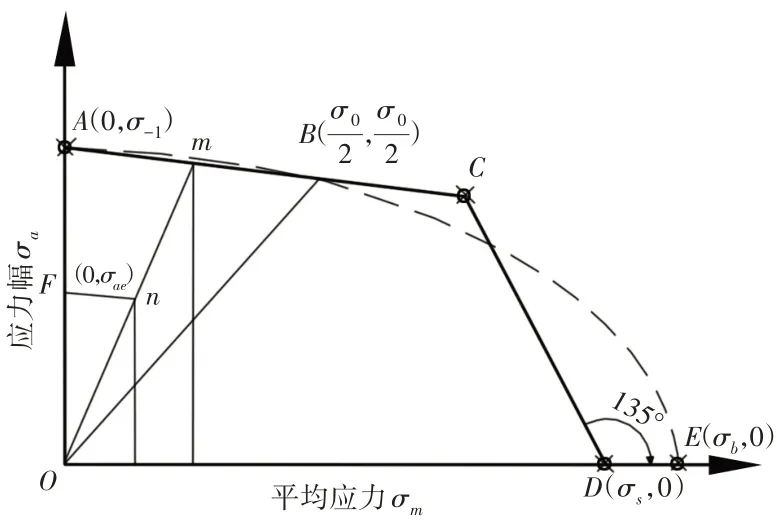
图1 极限应力曲线简化图Fig.1 Simplified Diagram of the Ultimate Stress
图中极限应力曲线由虚线ABE表示,其中A点应力坐标为(0,σ-1),是对称循环特性点,B点应力坐标为(σ0/2,σ0/2),是脉动循环特性点,E点应力坐标为(σb,0),是静强度极限应力点;A点应力坐标中σ-1为对称循环极限应力,B点应力坐标中σ0为脉动循环极限应力,σs为材料屈服极限,E点应力坐标中σb为材料抗拉强度极限。
图中简化的极限应力曲线由折线ACD表示,其中射线OB为结构脉动循环工作线,处于∠AOD角平分线位置;线段DC为结构的屈服极限线,C点由D点作的135°射线与AB延长线相交得到,D点应力坐标中σs为材料屈服极限应力。
由此得到简化后的封闭区域0ABCD,该区域即为结构疲劳设计标准限制疲劳安全的工作范围,基于该工作范围研究旋压皮带轮疲劳安全。

式中:Sσ—结构材料弯曲的疲劳安全因子;
σlim—材料疲劳极限应力。
对称循环下零件弯曲疲劳安全因子为:

由于应力幅影响因数较复杂,如零件形状尺寸、应力集中情况、表面质量等。
考虑到应力幅影响因数,根据[1,11]结构发生弯曲时,式(1)可以修正为:

式中:Kτ—结构剪切时有效应力集中因数;
β—表面质量因数;
ετ—结构剪切时形状尺寸因数;
λτ—剪切时的等效因数。
塑性材料同时存在弯曲变形和剪切变形时,其零件的工作应力应在椭圆范围内,如图2所示。
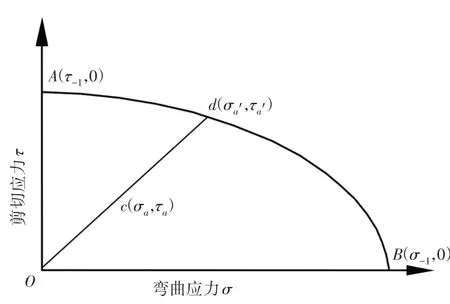
图2 复杂极限应力曲线Fig.2 Complex Limit Stress Curve

式中:S—复合变形下塑性材料疲劳安全因子;
S σ—材料弯曲时材料疲劳安全因子;
S τ—材料弯曲时材料疲劳安全因子。
3 旋压皮带轮有限元分析
3.1 问题描述及有限元模型
某公司生产的皮带轮由塑性材料旋压而成,这里根据[12]的设计参数,其包角设计为122.8°,包角范围内承载1.2MPa压力负荷,设计最高转速为10000r/min(1047rad/s)。
该塑性材料的力学参数,如表1 所示。需研究其在(100~1047)rad/s工作范围内的疲劳寿命。

表1 力学参数Tab.1 Mechanical Parameters
3.2 有限元模型
采用三维Solidwork软件对旋压皮带轮进行几何建模后导入有限元软件ANSYS Workbench。
为提高有限元求解精度,对导入的整个皮带轮采用六面体网格扫描划分,如图3(a)所示。划分的单元数为124630,节点数为607904。
载荷模型,如图3(b)所示。图中显示模型的边界条件分别有包角范围内的压力1.2MPa,内孔的固定支撑,旋转速度1047rad/s。

图3 皮带轮有限元模型Fig.3 The Finite Element Model of Pulley
3.3 应力仿真结果
皮带轮应力云图,如图4所示。
从图4(a)可以看出第一主应力最大值σmax为42.213 MPa,位于皮带轮受分布压力的带槽底部;
从图4(b)可以发现第三主应力最大值σmin为-27.46MPa,位于皮带轮受分布压力的带轮相对内侧;
从图4(c)可以得到最大剪应力最大值τmax为20.74MPa,位于皮带轮受分布压力的带槽底部,最小剪应力τmin约等于0。

图4 应力云图Fig.4 Stress Cloud Diagram
3.4 疲劳安全因子计算
等效因数为:

其中,Kτ剪切变形时,结构应力集中因数为1.88;
ετ尺寸因数为0.76;λτ不对称循环因数为0.21。
复合应力下,根据式(5)得复合疲劳安全因子:

4 转动速度对疲劳安全因子的影响
为了研究皮带轮旋转速度对疲劳安全因子的影响,转速从高到低分别取ω=900 rad/s、700 rad/s、500 rad/s、300 rad/s、100rad/s,计算结果,如表2所示。
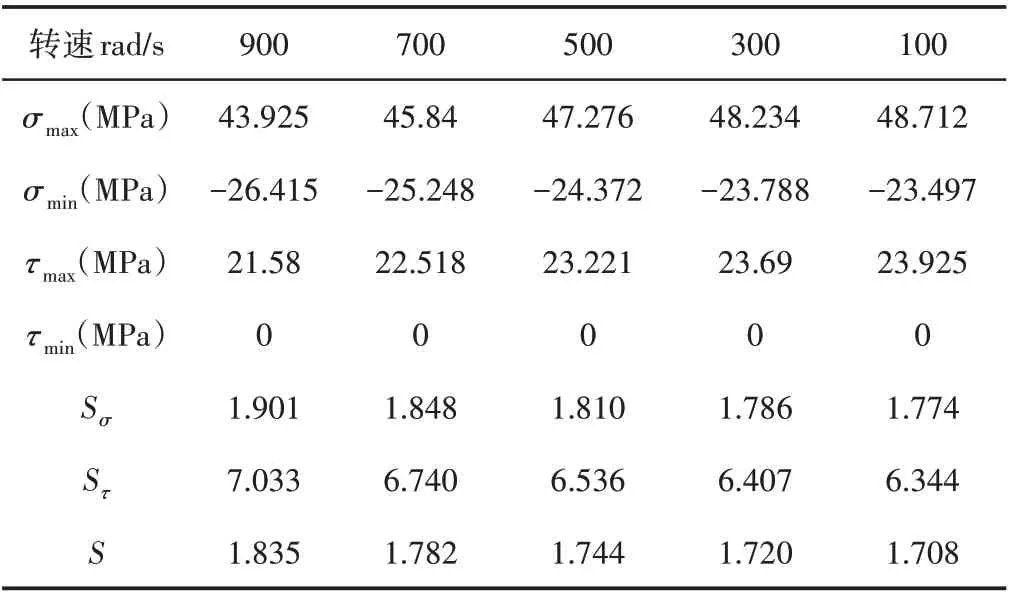
表2 疲劳安全因子Tab.2 Fatigue Safety Factor
对表2 数据进行分析,不同转速下,疲劳安全因子的变化,如图5所示。

图5 转速对疲劳安全因子的影响Fig.5 Effect of Rotational Speed on Fatigue Safety Factor
可以看出,Sσ、Sτ、S随转速提高而提高,但是提高幅度均不大,这是因为随着转速提高,其最大主应力和最大剪应力而减小,而最小主应力反而增大。
另外S最小为1.708,最大为1.835,均在许用综合疲劳安全因子[S]=(1.3~2.5)范围内,故该旋压皮带轮转速从100rad/s 变到1047rad/s,其疲劳寿命均安全。
5 结论
这里探讨了极限应力图和塑性材料同时存在弯曲变形和剪切变形时的疲劳安全工作范围,并借助有限元技术计算了旋压皮带轮的疲劳安全因子和研究旋转速度了从100rad/s 变到1047rad/s,其疲劳寿命均安全。
对疲劳安全因子的影响,得出如下结论:
(1)皮带轮在复杂应力状态下,其疲劳安全工作范围为椭圆形。
(2)皮带轮各疲劳安全因子Sσ、Sτ、S随转速提高而提高,但提高幅度不大,其中复合疲劳安全因子S最小为1.708,在许用疲劳安全因子范围[S]=(1.3~2.5)内。
