听骨链仿生隔振模型的动态特性分析与实验研究

张金萍，王婉莹，李允公，李明智

（1.沈阳化工大学机械工程学院，辽宁 沈阳 110142；2.东北大学机械工程与自动化学院，辽宁 沈阳 110004）

1 引言

中耳是人耳中声音传导的重要组成部分，人的中耳起阻抗分配的作用，具有在强声下的保护功能，其中中耳的听小骨起到了至关重要的作用。听小骨是由锤骨、砧骨、镫骨三块骨头组成的听骨链，具有减小镫骨与锤骨位移比的功能，是一个典型的动力学系统。对中耳三维模型进行动力学分析有助于研究中耳的减振机理，尤其是韧带等对中耳减振作用的影响，对听骨链系统减振特性的设计研究具有重要意义。

早期学者们多采用电路模型、多体模型[1]等对中耳进行建模来模拟中耳在某些特定条件下的传声规律，但更多的学者采用有限元方法观察听骨链的力学行为和细致的振动模式[2]。文献[3]用有限元方法建立了包括砧镫关节、肌肉韧带等的三维模型来研究中耳压力传导以及听骨链的振动模式。文献[4-5]使用Solidworks软件建立人体中耳的有限元立体模型，这种方法对体积小、几何构造复杂的结构更有优势。通过学者们的研究发现，声波经过外耳道引起鼓膜振动，振动信号经过听骨链的传递后压力增强，振幅减小，听骨链可作为设计隔振系统的参考模型。Adams是一种用于机械系统动力学自动分析的软件，它可以输出位移曲线、速度曲线以及加速度曲线[6]，可用于预测机械系统的性能以及运动范围等[7]。文献[8]通过Adams建立的振动模型对同步振动沉桩系统的设计提供理论和实际工程依据；文献[9]借助Solidworks软件建立Stewart并联机构的三维模型并导入Adams中进行运动学仿真分析，为义耳成型方案的样机制造和控制系统设计奠定基础。因此在听骨链的仿真分析中使用Adams虚拟样机技术是发展迅速和前沿的方法。

综上所述大部分对中耳的研究都只是单独针对听小骨，对包括韧带系统的整体研究较少；对听骨链的机械化应用少有涉及，也没有将听骨链的振动特性应用到更多的领域，现有研究中很少有使用Adams分析听骨链的运动学特性。

通过建立听骨链的Adams虚拟样机模型来对听骨链的运动状态进行仿真，设置不同的激振力，得到对应不同频率下听骨链的动态特性。通过对听骨链仿生隔振系统进行建模并打印实体，测试了其在不同频率及不同负载下振动特性，从而对仿真结果进行实验验证。

2 听骨链模型的建立

2.1 听骨链的简介

听小骨由韧带和肌肉固定在鼓室中，锤骨主要由锤骨上悬、锤骨前、锤骨侧三条韧带固定在中耳腔中。

砧骨韧带系统包括砧骨上悬和砧骨后两条韧带，镫骨仅由镫骨环韧带控制。听骨链周围还有鼓膜张肌和镫骨肌。当传递高频声波信号时，锤骨因鼓膜张肌收缩作用沿声波压力方向内移；镫骨肌控制镫骨位移量，使其绕镫骨中轴线转动。

姚文娟[10]得到听骨链系统中实际韧带结构及位置，如图1所示。

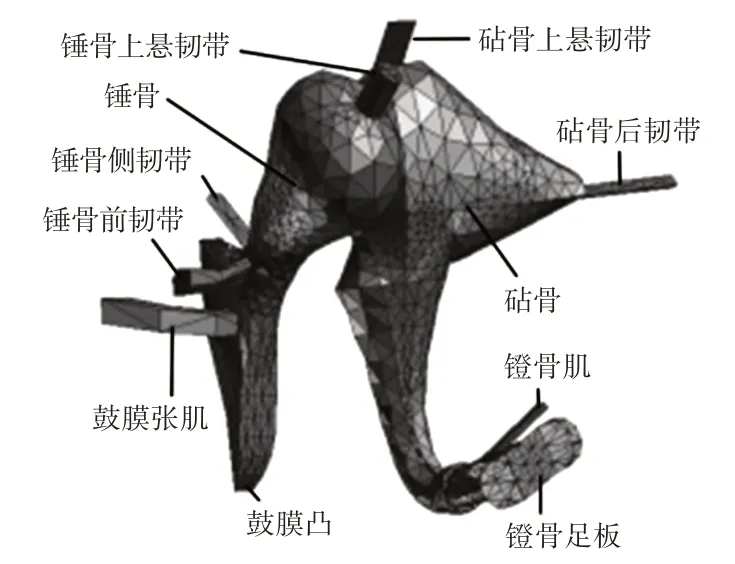
图1 听小骨结构模型Fig.1 Auditory Ossicles Structure Model

2.2 听骨链建模基本假设

对比有关学者对听骨链材料属性[11]的研究后，发现听骨链泊松比约为0.3，由于锤骨和砧骨不同位置的杨氏模量也不同，选取每块小骨的杨氏模量均值作为听骨链的材料参数。不同于锤砧骨材料的属性，镫骨材料的杨氏模量和密度是均匀的。

2.3 参数及模型的建立

2.3.1 仿真三维模型的建立

根据人耳中听骨链形态结构进行建模优化以及分析，采用三维软件对锤骨、砧骨以及镫骨进行建模，并导入到仿真软件中实现建模。

听小骨各结构材质属性，如表1所示。

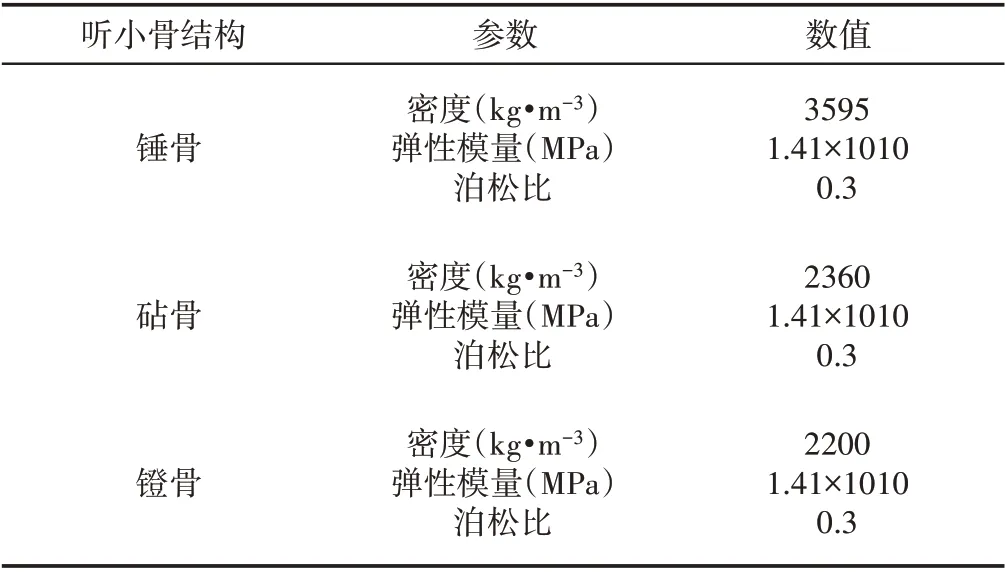
表1 材质属性Tab.1 Material Properties

2.3.2 仿真模型的约束添加

建模过程中设置镫骨底板以及箱体外壳和大地固定连接，设置砧骨与镫骨以及镫骨与镫骨底板之间为移动连接。

通过柔性连接模块来建立锤砧关节以及韧带，由于人耳在受到较小声强刺激时引起鼓膜振幅较小，锤砧骨呈整体运动状态，受到外部声强较大时锤砧关节会产生相对滑移，从而减小镫骨位移量来保护内耳，本文采用扭转弹簧来模仿锤砧关节。

通过研究听骨链空间结构的形态[12]发现，三块小骨大概呈N形固定于中耳腔中，在声传导过程中其角度大小允许在一定角度范围内变化。听小骨角度参数，如表2所示。

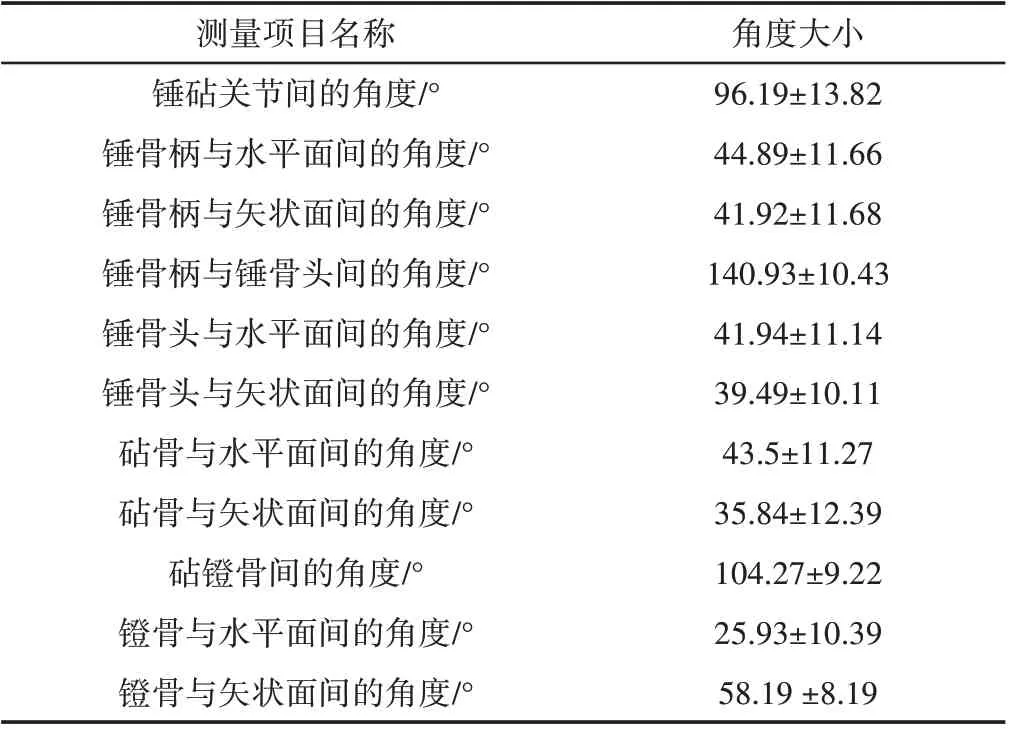
表2 听骨链角度参数Tab.2 The Angle Parameters of Ossicular Chain

借鉴图1三维模型，在建模时采用弹簧来模拟韧带的功能，从而实现对听骨链系统的仿真，得到最终的听小骨仿真模型，如图2所示。

图2 听小骨仿真模型Fig.2 Auditory Ossicles Simulation Model

相应的弹簧模拟韧带的参数，如表3所示。

表3 各弹簧参数Tab.3 Spring Parameters

3 听骨链运动特性仿真分析

通过调整函数的幅值以及频率来仿真听小骨结构受到不同力的时候的运动状态，设置激励函数为F=10sin(350t)，仿真时间t=5s，进行运动学仿真。得到锤骨、镫骨的位移、速度、加速度随时间变化的仿真曲线，放大后，如图3所示。由图3可知，当振幅为10时听骨链系统运动较为稳定，可在此振幅下观测锤镫骨在不同频率下运动状况，幅值比仿真结果，如图4所示。

图3 听小骨仿真曲线Fig.3 Auditory Ossicles Simulation Model

图4 振幅为10时不同频率下听骨链系统运动幅值仿真结果Fig.4 Simulation Results of Oscillating Chain System Motion Amplitude at Different Frequencies with Amplitude of 10

4 实验验证

为验证听骨链系统的振动特性，进行听骨链系统的不同频率以及不同振幅的振动测试，搭建的实验台，如图5所示。在锤骨底板和镫骨底座上各安装一个传感器，锤骨为输入端，镫骨为输出端。采样频率为5120Hz，采样时间为6s，采集30组数据。采用DASP信号采集分析系统进行信号分析。

图5 听骨链隔振系统实验台Fig.5 Ossicular Chain Vibration Isolation System Test Bench

4.1 简谐激励实验结果

由于听骨链系统往往会受到不同大小的激振力，所以采用偏心轮电机来模仿系统工作时受到简谐激振力。通过在底板上施加不同重量的砝码来模拟不同负载下即不同振幅下系统的频率特性。通过采集不同频率下锤、镫骨的加速度信号来分析该系统的动力学特性和相关的性能。采集锤骨底板和镫骨底板输出信号加速度幅值变化曲线，如图6所示，由图可知，动力机械产生的简谐振动信号经该减振系统的传递后，镫骨底板输出信号较锤骨足板输出信号更为光滑。

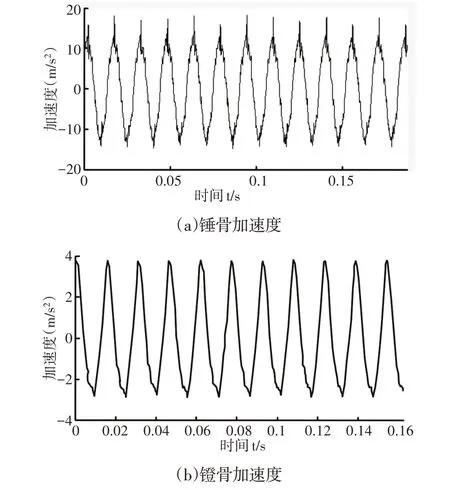
图6 减振器的输入与输出加速度Fig.6 Input and Output Acceleration of Shock Absorber

图7 显示的是系统正常工作时，负载为100N、300N、500N、800N时锤、镫骨在不同频率时加速度幅值比，实验中通过调节电压的大小来控制偏心轮电机的转速从而调节其频率。

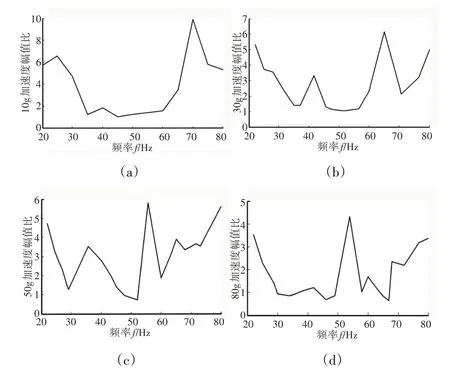
图7 不同负载时隔振系统频率特性Fig.7 Frequency Characteristics of Vibration Isolation System under Different Loads

将仿真获得的振幅为10时不同频率下锤镫骨加速度幅值比曲线，如图4（b）所示。实验中采集数据生成的曲线进行比较，如图7（a）所示。对比结果表明，所绘制模型的锤骨与镫骨的频率特性仿真曲线与实验采集数据生成曲线的趋势几乎是一致的，验证了听骨链仿真结构设计过程中机构模型参数设置的正确性。系统在（30～50）Hz 的频率范围内减振效果相对较为稳定，在50Hz后随着负载的增加系统的隔振峰值依次降低，且达到隔振峰值所对应的频率也依次减小，可能与负载改变了系统的固有频率有关，所以对系统的共振特性进行研究。

4.2 冲击激励实验结果

实验采用锤击法模拟系统受到冲击载荷，通过敲击锤骨底板分别测得锤骨加速度时域信号x(t)和镫骨加速度时域信号y(t)，通过傅里叶变换得到系统的幅值谱，如图8所示。

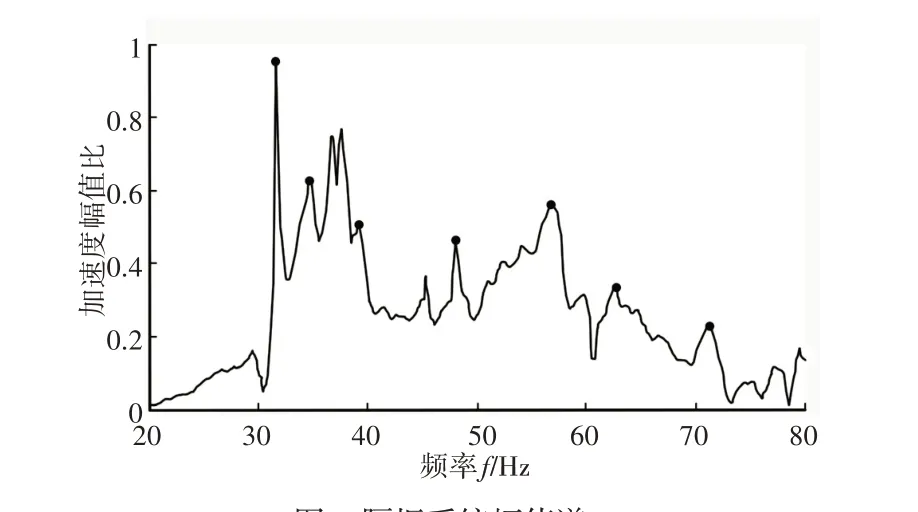
图8 隔振系统幅值谱Fig.8 Amplitude Spectrum of Vibration Isolation System

由上图可知，频率在31.5Hz，35Hz，39Hz，48Hz，57Hz，63Hz和72Hz时系统会出现共振峰，在（39～63）Hz频率范围内运行较为稳定，在72Hz以后系统趋于稳定状态。

为了验证负载会改变系统固有频率，对听骨链隔振系统在不同负载下频率响应进行实验测试研究，负载为100N、300N、500N、800N时系统的频率响应，如图9所示。

图9 不同负载隔振系频率响应Fig.9 Frequency Response of Vibration Isolation Systems with Different Loads

研究发现，当振源为简谐激励和冲击激励时隔振系统都具有减振特性，且随着负载的增加，隔振系统在达到最大峰值时所对应的固有频率减小，导致该隔振系统达到的极大值点和对应的频率都减小。随着负载的减小，隔振系统的隔振能力将会有所提高，最大隔振峰值所对应的频率逐渐增大。后期还需要进一步研制真实样机，进行听小骨模型的试制并分析、修正听小骨减振模型的效果。

5 结论

（1）建立了听骨链隔振系统的Adams仿真模型，并分析了锤镫骨加速度幅值比与频率之间的关系，结果表明，在（20～50）Hz频率范围内系统能较平稳的工作，在（50～80）Hz范围内，锤砧骨会发生相对扭转，80Hz后系统会继续稳定工作，从而达到减振的作用。（2）实验结果显示，在简谐激励作用下和冲击激励作用下隔振系统都具有减振特性，系统的频率特性的拐点与共振频率有关，随着负载的增加，隔振性能有所降低，由于系统达到最大峰值时所对应的共振峰的频率逐渐减小，所以系统工作时达到最大减振峰值所对应的频率也依次减小。（3）研究表明此听骨链隔振系统模型与人耳听小骨具有相似运动特性，仿真及测试信号可以有效的表征该系统的振动特性，在分析此听骨链隔振系统的频率特性、减振效果和研究其适用频率范围和将其应用于减振领域方面有一定的实际意义。