沙发框架T型和L型节点抗弯性能有限元分析

2022-01-13李伟康钟文翰胡玲玲姚腾飞余肖红

家具与室内装饰 2021年12期

■李伟康，张婷，钟文翰，胡玲玲，姚腾飞，余肖红

(1.浙江农林大学化学与材料工程学院，浙江杭州 311300；2.喜临门家具股份有限公司，浙江绍兴 312000； 3.浙江省轻工业品质量检验研究院，浙江杭州 311100）

ANSYS有限元软件由于其强大的结构分析、动力分析、磁电流体分析等功能，为工程师提供了一种有效的技术手段来预测模拟工程中的各类情况。有限元法在家具结构上的应用较多针对板式家具或整体的分析[1]，而对家具结构节点的分析需要进一步完善。对于家具的设计和生产，有限元分析的一个优势是在家具设计阶段能够评估家具整体或部件的力学性能，从而加快家具的设计生产周期。

1 有限元分析在家具节点中的应用概述

在一些家具设计中，家具的各个部件会被有意地做大尺寸，其目的在于确定不超过许用应力的情况下，保证每个部件都能够安全地承受所受到的力。但对于一些需要精确被加工的受力部件，有限元法无疑是一种可靠的设计方法来确定部件的有效尺寸。随着计算机的发展，有限元法已经成为有效的结构分析方法。相关学者将家具中的节点结构主要分成L型和T型结构，T型结构多用于实木框架的中档接合部位，L型结构多用于实木框架的端部接合处[2]。通过有限元法可以简化、模拟和分析结构中关键节点的抗拔能力和抗弯能力，进而来评估家具结构的性能。奚茜等[3]人通过试验测试和有限元分析，完成了对黄荆木重组材制备的3种典型家具节点的T型试件抗拔力研究，结果表明有限元法能有效地应用于该节点的抗拔力的测试。胡文刚等[4]人通过有限元分析法分析了不同过盈量下榉木椭圆榫接合T型节点抗弯强度，并通过实验测试进行了验证，也表明了测试结果与有限元结果有较好的相关性。Derikvand等[5]人利用ANSYS Workbench有限元软件和实验测试研究了T型试件中不同榫头长度和厚度对节点抗弯承载力的影响，结果表明了有限元预测的节点最大剪应力和破坏模式与测试的结果具有一致性。柯清[6]在验证田口试验方法结合ANSYS有限元模拟分析的可行性与有效性后，优化了榆木、松木、改性杨木三种材料家具L型试件双圆棒榫节点和整体椅子的最大等效应力与形变量。何风梅[7]通过有限元法对板式家具中的T型和L型角部试件强度的分析，优化了板式家具中的连接结构和连接方式，并通过试验测试得到了良好的验证。通过有限元的应用情况可知，有限元法可以有效便捷地分析出家具关键部位的受力情况，但不同材料的定义、荷载加载方式、试件尺寸、约束设定等都影响着仿真结果，因此，对于在有限元中家具受力结构的简化和影响因素的分析还需要进一步完善。

沙发框架的设计一定程度上决定了沙发的质量[8]，因此，有必要对沙发框架节点的不同试件形式进行抗弯性能分析。有限元法可以在构建沙发中关键结构部件模型后，对其在受载时的力与位移、应力与应变等力学情况进行快速准确的分析，从而有效地减少研究工作量。

本文首先对比了T型节点在刚性连接下的理论计算结果和有限元仿真结果，并进一步利用有限元法研究了半刚性连接中，沙发框架的L型和T型节点分别在圆钉和直榫两种连接方式下抗弯性能的差异。其次，在静力学分析的基础上，通过SPSS分析和响应面设计分析，分析了各因素对L型和T型节点的抗弯性能的影响。

2 ANSYS Workbench静力学模块分析

ANSYS Workbench软件静力学分析流程包括前处理、边界条件定义和后处理。前处理包含建模、材料定义和网格划分三个部分。建模时为了减少结果的应力集中和应力奇异的现象需要对模型进行简化[9]，可以根据理论和经验判断模型的几何细节的相关性。在完成模型的构建后，需赋予模型密度、弹性模量、泊松比等材料参数。网格的划分则需要考虑网格的数量，可以考虑求解的目的，若以位移求解为目标，网格数量相对减少有助于结果的收敛，而若以力值求解为目标，网格数量相对增加更有利于得到精确的结果。边界条件包括自由度的约束和荷载的定义，只有根据实际的工程情况设置边界条件，才能求解出正确的结果。后处理则可以根据需求对其应力与应变、力与位移、能量和体积变化等情况进行查看。

静力学分析主要是研究静止或者匀速状态下的结构响应，它不考虑惯性和阻尼效应，以及速率的变化。对于有限元的分析，其关键在于材料的定义、模型的简化和边界条件的设置三个部分。

2.1 沙发框架材料定义

本文沙发框架选用松木[10]和刨花板[11]两种材料进行分析，具体参数见表1和表2。由于松木材料的各向异性，因此，需要分别对X，Y，Z三个方向的弹性模量、泊松比和剪切模量进行定义。

表1 松木材料属性表

表2 刨花板材料属性表

2.2 沙发框架节点模型的建立

根据板式零件的测试方法[12-13]，确定刨花板尺寸为100 mm×150 mm×15 mm，两块板以T型和L型形式组成试件，接口采用市场上常用的几种圆钉连接，圆钉间距为32 mm。松木材料以木档榫接方式组成T型和L型试件，榫头与榫眼间隙配合0.5 mm厚的胶粘剂，沙发框架中木档的截面尺寸可取20 mm×30 mm[14]，本文横竖向试件尺寸均为20 mm×30 mm×150 mm。具体见表3和图1。

表3 模型整体尺寸参数

2.3 边界条件设置与后处理

2.3.1 节点刚性连接

■图1 沙发框架节点试件模型

■图2 边界条件设置示意图

■图3 总变形量和应变结果云图

■图4 L型和T型节点总变形结果（L型：松木木档连接方式④、刨花板连接方式⑤ T型：松木木档连接方式⑩、刨花板连接方式⑨）

■图5 刨花板连接方式①-⑨

■图6 刨花板连接方式①-③与④-⑥中最大位移与圆钉直径的关系

经典力学计算中，沙发框架节点的连接被视为刚性连接，这里以刨花板T型连接为例，对比理论计算的结果和有限元模拟的结果。首先将该结构视为悬臂梁模型[15]，并在横杆端部施加150N的竖向力，故横杆的挠度w和应力的计算如下：

式中：w为挠度量（mm）；F为端部载荷(N)；L为力到节点的力臂长度(mm)；E为材料的弹性模量(Mpa)；I为截面惯性矩(mm4)；M为弯矩(N·mm)；W为抗弯截面系数（mm3）；b为截面长度(mm)；h为截面高度(mm)；在ANSYS Workbench中将竖向板固定，横向板、圆钉与竖向板的接触设定为绑定，并在横向板端部施加150 N的荷载，边界设置如图2所示，有限元运行结果如图3所示。

查看有限元结果，其最大变形为1.9349 mm，Von Misses应力为5.8611 MPa。与力学公式计算的挠度和应力的偏差分别为1.33%和2.31%，二者的误差皆在合理范围之内。

2.3.2 节点半刚性连接

与经典力学理论不同的是，实际中沙发框架的T型和L型节点连接，一般都被认为半刚性连接[16]，在节点连接处存在一定分离量。因此，在有限元模拟时候需要考虑过盈配合或间隙配合，本文在模拟时考虑了试件之间的不同配合量。

通过改变刨花板和松木木档的连接接口的尺寸和连接形式，来比较沙发框架节点的抗弯性能。有限元在模拟节点半刚性连接时，仅对竖向试件的底部进行固定，圆钉和胶粘剂与试件的接触、横向试件与竖向试件的接触设定均为有摩擦（Frictional），摩擦系数为0.5。胶粘剂的弹性模量定义为400 MPa，泊松比为0.3。圆钉材料选用ANSYS中默认的结构钢。节点半刚性连接下T型和L型试件的总变形结果如图4所示。

近年来，高校大学生因心理疾病、精神障碍等原因发生的自杀、致伤、伤害他人的案例时有发生，引起社会的广泛关注和深刻反思。

2.4 仿真结果对比与分析

2.4.1 刨花板试件仿真结果

■图7 松木木档连接方式①-⑩

■图8 松木木档连接方式②与⑨中产生的Von-Mises

■图9 竖向作用力、刨花板的弹性模量与试件最大位移3D响应图

■图10 Matlab拟合结果

刨花板试件L型和T型在圆钉连接方式下的最大位移量（挠度）对比如图5所示。其连接方式①-③和④-⑥中的最大位移与圆钉直径的关系如图6所示。

从图5和图6中可以看出，圆钉直径的大小对刨花板试件的抗弯性能有着明显的影响，且在一定范围呈现出线性关系。比较图5中的④-⑥与⑦-⑨，可知在圆钉连接下L型试件的最大位移量略大于T型试件。

2.4.2 松木木档试件仿真结果

L型和T型松木木档试件在直榫连接方式下的最大位移量（挠度）如图7所示。为进一步分析L型和T型试件形式对节点的影响，选取了其中榫眼尺寸为16mm×11mm×12mm的L型和T型试件的Von-Mises应力进行比较，如图8所示。

从图7中可以看出增加榫头三个方向上的尺寸，能提高试件的抗弯性能。比较图7和图8中试件连接方式②和⑨的结果发现，T型试件的最大位移量73.016mm明显小于L型试件的最大位移92.125mm，而T型试件横向试件中产生的Von-Mises应力值为103.09Mpa明显大于L型试件的70.518Mpa，分析其原因主要是:相对于T型试件，L型试件接口在试件边部所产生的过大位移，导致了L型试件竖向试件的弯曲变形程度要大于T型试件，从而影响了其接合强度。

3 SPSS方差分析和ANSYSWorkbench响应面分析

3.1 SPSS方差分析

利用SPSS方差比较了T型和L型两种试件形式下节点的抗弯性能，同时进一步分析了圆钉直径和榫头尺寸对试件受力端最大位移量的影响。方差分析是将试验数据的总的离差平方和SST分解成各因素的离差平方和SSt与离差平方和或误差平方和SSe，并基于离差平方和SSt与离差平方和或误差平方和SSe除以各自自由度所得到的均方，以均方之比F统计值作为判断各因素显著程度的一种科学手段[17]。影响沙发节点抗弯性能的各因素的方差分析结果见表4-表7所示，其中因素a：T型和L型；因素b：圆钉直径；因素c：钉长；因素d：榫长；因素e：榫宽；因素f：榫深。

表4 T型和L型刨花板试件试验方差分析结果（④-⑨）

表7 L型实木木档中不同尺寸榫头试验方差分析结果（②-⑦）

由表4-表5可知，因素b的显著性分别为p=0.002<0.05和p=0.014<0.05，即圆钉的直径对T型和L型刨花板试件的抗弯性能存在显著影响。表6表明，因素a的显著性为p=0.005<0.05，同时，因素f的显著性为p=0.026<0.05，说明T型和L型试件形式对榫接下的实木木档的抗弯性能存在显著性影响，且榫头的深度与其抗弯性能也呈现显著性关系。由表7可以看出，因素d的显著性为p=0.018<0.05，即相对于榫宽与榫深，榫头的长度对榫接下的实木木档的抗弯性能存在显著性影响。分析原因：无论是增加圆钉的直径或增加榫头的深度和长度，都是增加了T型和L型试件在作用力方向上的受力面积，进而显著影响了其挠度[18-19]。

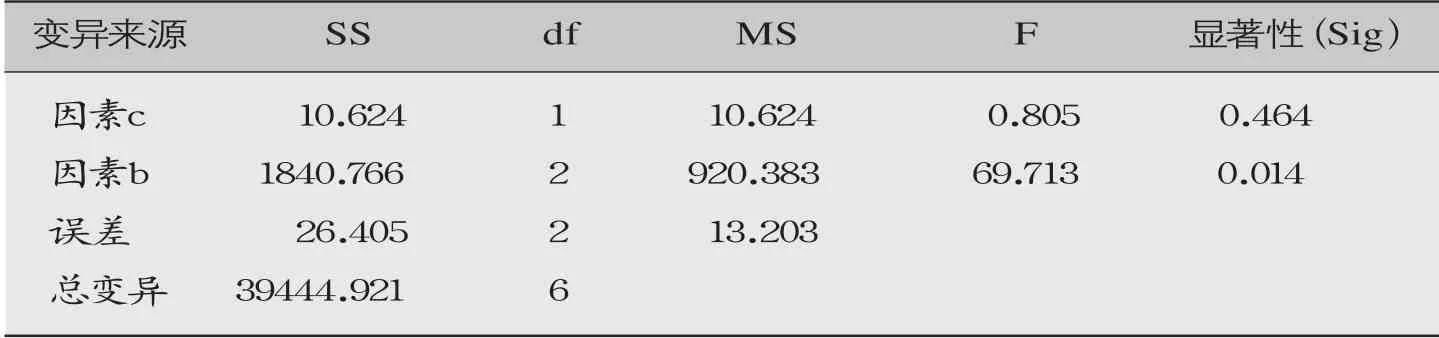
表5 L型刨花板试件试验方差分析结果（①-⑥）

表6 T型和L型实木木档试件试验方差分析结果（①-③与⑧-⑩）

3.2 ANSYS Workbench响应面分析

响应面分析的实质是通过一系列试验数据，采用多元二次回归方程来拟合因素和响应值之间的函数关系[20]。即在静力学求解的基础上，将ANSYS Workbench中模型参数化，对模型中的变量和因变量进行定义和分析。以刨花板连接方式⑨为例，基于静力学仿真结果，进一步研究刨花板的弹性模量和竖向作用力与L型节点的抗弯性能的三者关系。首先，在ANSYS Workbench中将刨花板的弹性模量、竖向作用力作为输入参数，将最大位移量作为目标参数。其次，选择Design Exploration 模块下的响应面分析，运用Response Surface 分析，选择默认的DOE类型中心组合设计，并设置参数上下界，在更新响应面上的输入和输出因素的关系后，在响应面类型中选择标准二阶响应模型查看结果[21]。Design Exploration 子模块组合设计点响应结果如表 8和图9所示。

表8 竖向作用力、刨花板的弹性模量与试件最大位移的响应结果

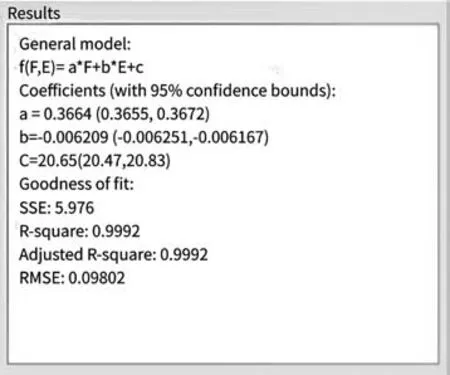
从表8和图9的响应面分析结果来看，可以明显看出T型节点的抗弯性能与弹性模量、竖向作用力存在线性关系。因此，可以构造多元回归方程，采用Matlab软件中的拟合工具（Curve Fitting Tool）进行参数拟合，拟合结果见图10，其关系式为f=0.3664F-0.006209E+20.65，其中F表示竖向作用力(N)，E表示弹性模量(Mpa)，f表示试件的最大位移(mm)，a、b、c表示系数。