对硬币在不同环境下转动的分析

方尤乐，王天骁

(北京大学 地球与空间科学学院，北京 100871 )

硬币(或圆盘)模型是实际应用中一类常见而重要的模型[1]．在以往的文献中，硬币的许多典型问题已经得到了很好的解决，如圆盘在理想粗糙平面上的绕圈转动问题[2]、滚动与转动的稳定性问题[2]、圆盘在一般平面上运动过程中的能量耗散问题[3]、各种摩擦耗散模型下的运动规律问题[4]等．但大多是基于拉格朗日力学方法分析运动模式，少有用普通物理的方法求解运动方程和给出直观运动表述．文献[2]中对硬币的特殊运动模式下稳定性问题进行了较为详细的讨论，但它对于不同运动问题采取了不同的分析方法．为了能给出系统性讨论，本文分析了硬币在空中、地面上、冰面上的运动情况，讨论了硬币稳定绕圈运动过程中的微小章动问题，并将其结果用于分析特殊运动模式．本文还利用解得的一般方程对硬币的运动进行了数值模拟，倾角随时间变化图像有助于更加透彻地理解硬币的运动，并有助于认识其他运动规律．

1 模型与基本方程的建立

我们约定，一枚硬币是质量为m、半径为r的均匀圆盘形刚体，厚度忽略不计，与实际情况有一点差异．硬币的中心(也是质心)为O．令I1为硬币绕自转轴的转动惯量，I2为硬币绕其一条直径的转动惯量．那么有

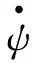
图1 硬币坐标系

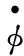
(1)

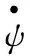
ω=ωr+Ω=

(2)

(3)

由硬币的对称性可知，x1、x2、x3三个坐标轴是硬币的一组惯性主轴．因此在坐标系Ox1x2x3中，硬币的惯性张量为

所以硬币相对于O点的角动量为

LO=Iω=I2ω1i+I2ω2j+I1ω3k

(4)

角动量随时间的变化率为

(5)

设硬币在相对于随O点做平动的参考系中的转动动能为Ekr，则

(6)

2 在空中转动

(7)

由于硬币只受到竖直方向的外力，硬币相对于O点的角动量在ez方向上的分量不变．设这一分量为b，由式 (1)、(3)、(4)可得

(8)

硬币的转动动能守恒，Ekr为常量．将式 (7)、(8)代入式 (6)，整理得关于θ的一维运动方程.

(9)

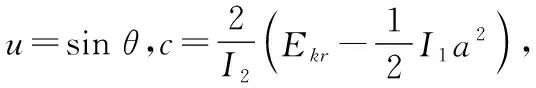
(10)

积分可得

(11)

(12)

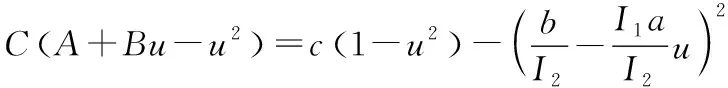
(13)

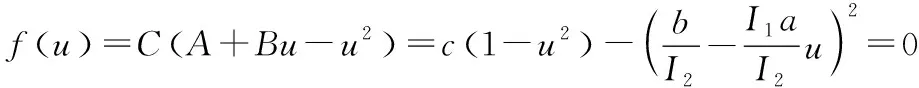
从另一个角度分析这个问题可以得到更直观的运动描述[5]．如图2所示，在硬币坐标系中画出角动量与角速度矢量．由ω×LO在k方向上无分量可知，ω、LO、x3轴共面(图中的阴影部分)．x3轴上所有点的瞬时速度在每时每刻都垂直于该平面，而LO在质心平动参考系中是不变的矢量．所以x3绕LO的方向匀角速转动，同时，硬币绕自身的轴匀角速转动，所以ω在x3轴上的投影ω3不随时间变化．设LO与k的夹角为θ1，则由式 (4)可得

(14)

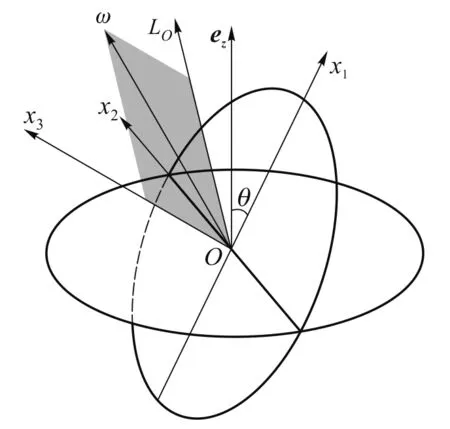
图2 角动量与角速度矢量

为了求硬币绕LO的进动角速度ωpr，应利用平行四边形法则将ω沿x3轴和LO的方向分解．其中第一个分量不会使x3轴移动，所以第二个分量就是ωpr，计算可得

(15)

3 在地面上转动

硬币在真实的地面上运动时可能会有滑动摩擦，导致复杂的难以分析的运动．这里假设地面的摩擦系数充分大，硬币与地面之间不会产生相对滑动，即硬币与地面的接触点P为速度瞬心，并且不计滚动摩擦．下面先求解特殊运动问题，再求出一般的运动方程，最后再利用一般方程深入分析特殊运动模式．

3.1 绕圈转动问题

图3 绕圈转动的正视图

-rω3=Rωpr

(16)

将式 (2)中的变量替换为ωpr、ω3，得硬币的转动角速度的新表达式

ω=ωprcosθi+ω3k

(17)

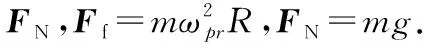
M=-Ffrcosθ+FNrsinθ=

(18)

将式 (4)、式(17)整理可以得到LO的表达式．LO的竖直分量不随时间变化，其水平分量为

L=-I1ω3cosθ+I2ωprcosθsinθ

(19)

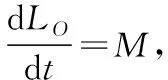
Lωpr=M

(20)

将式 (16)、(18)、(19)代入式 (20)化简，即可求出ωpr的表达式

(21)

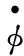
现对摩擦系数及绕圈运动半径的范围进行定量分析．设桌面的最大静摩擦系数为μ，则

所以，当 tanθ≤μ(1+I1/mr2) 时，绕圈运动的半径R可以是任意值．当 tanθ>μ(1+I1/mr2时，R应满足以下关系式

(22)

再定性分析该运动的稳定性．若倾角为θ的硬币在做匀速绕圈运动时，突然给硬币一个微小的扰动使它的进动角速度ωpr减小，此时摩擦力大小减小，合力矩增大，同时式(19)中角动量的水平分量L在减小，所以角动量水平方向的矢量转动的角速度会超过ωpr，这导致在下一时刻，图3中硬币的角动量有垂直纸面向外的分量，导致θ增大，这将使得ωpr恢复甚至超过原来的大小. 所以可以猜测，在一定条件下硬币的绕圈运动是稳定的，在微扰后可能会发生章动．

3.2 一般问题

由于硬币绕O的角速度为ω，O在绝对参考系下的速度为

(23)

由此可以计算O的加速度：

(24)

由质心运动定理可求出P点受力

FP=maO-mg=

mαO+mgcosθi+mgsinθk

(25)

(26)

比较i方向上的分量可得

(27)

再列出硬币的机械能守恒式:

mgrcosθ=E

(28)

式(28)两边对时间t求导，再将式 (26)、(27)代入整理得

(29)

式(26)、(27)、(29)及式(3)就是硬币在摩擦因数充分大的水平面上运动的基本方程．经过对照，它与文献[2]中推导的基本方程是一致的．该方程难以求解，但可以利用它做数值模拟以发现新的规律，还可以利用它验证一些特殊情况的运动方程．

再将式 (16)代入消去ω3，就求出了与式 (21)相同的ωpr的表达式．

3.3 绕圈转动中的微小章动

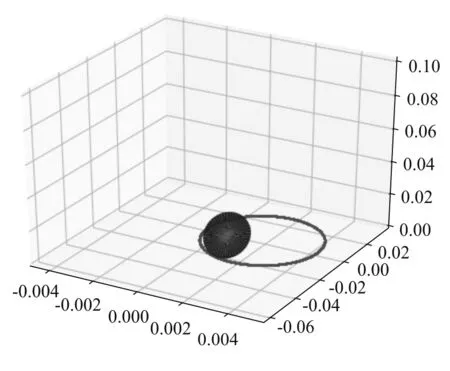
图4 绕圈转动的计算机模拟图像

在ωpr、ω3、θ符合式 (21)且满足另一些条件时，硬币会做稳定的匀速绕圈运动．当硬币受到微扰时，就会产生微小的章动，θ在小范围内“振动”．这一节主要利用上一节求出的基本方程 (26)、(27)、(29)来求解微小章动的周期及稳定的条件．这里定义θ从极小值处随时间增大，后又随时间减小到极小值的过程为一个章动周期．

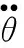
由式(26)、(27)可得

(30)

(31)

(32)

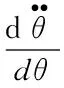
(33)

(34)

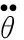
-k(θ-θ0)+o(θ-θ0)

因此，当k>0 时，绕圈半径为R，倾角为θ0的运动是稳定的．若对其做小扰动，则将发生微小章动，周期为

(35)

其中k是有关R、θ0、m、r的常量，表达式为式(34)．将5.1节的硬币数据代入 式(34)后，可得到与文献[4]的式(5.22)类似的结果．

3.4 一些特殊的运动模式

利用上一节的结果可以分析一些特殊的运动模式的稳定性．例如当硬币在做定点转动时，当转速较高时，硬币可以保持近似垂直且稳定不倒．此时可以看成θ0≈0,R≈0 的绕圈运动，所以 式(34)近似为

因此，为了使硬币的横向转动处于稳定状态，转动角速度需满足

(36)

这表明，以同样的角速度转动时，硬币的半径越大，转动越稳定．

我们用计算机程序对硬币的横向转动进行了数值模拟，并在开始时对硬币的状态进行微扰．利用5.1节中的硬币数据，式(36)的计算结果为 |ωpr|>25.3 s-1．图5中绘制了以4种角速度进行定点转动的硬币的θ关于时间的图像，可见当ωpr满足条件时，θ能在某一个极小的范围内“振动”，所以是稳定的．图线的形状近似于简谐波，其周期与 式(34)、(35)的结果是一致的．

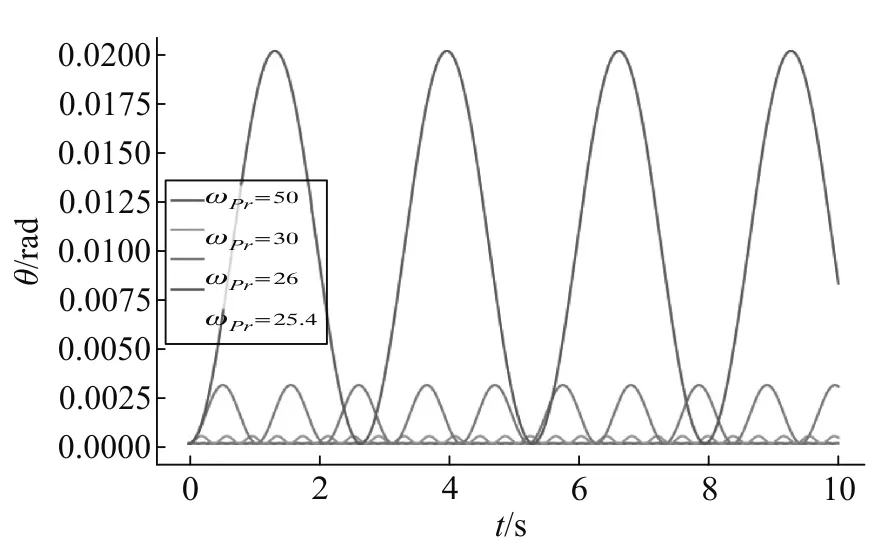
图5 硬币定点转动时倾角关于时间的图像(ωpr>25.3s-1)

图6显示了当 |ωpr|<25.3s-1时θ的变化图像．可见当ωpr小于 25.3s-1时，θ将大幅摆动，且随着ωpr的减小，摆动幅度增大，趋向于π/2．从图中还可以观察到新的规律，倾角θ虽然不会在 0 附近稳定振动，但仍存在周期性的变化，且周期随着ωpr的减小而减小；倾角过极小值点后一段时间突然增大，到了极大值点后又突然“反弹”．这种周期性变化可以由能量守恒以及系统的时间反演不变性解释．这种现象也在实验过程中出现，但由于有能量损失，所以实验中周期性变化幅度逐渐减小．

图6 硬币定点转动时倾角关于时间的图像(ωpr较小)

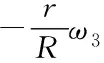
因此，为了使硬币沿直线滚动处于稳定状态，滚动角速度需满足：

(37)

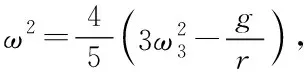
我们也对这种情况进行了数值模拟，在不同的滚动角速度下，硬币的θ关于时间的图像如图7和图8所示．(37)式的计算结果为 |ω3|>16.3s-1，这与图像的结果是一致的．当 |ω3|<16.3s-1时，硬币的倾角将产生大幅度地摆动，且呈周期性变化，而此时硬币不再沿直线滚动．

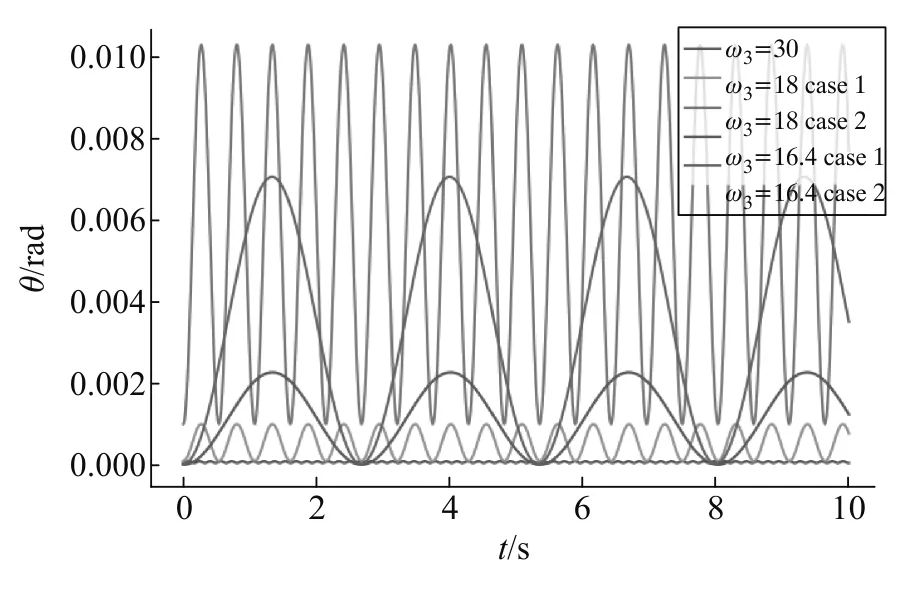
图7 硬币滚动时倾角关于时间的图像(ω3>16.3s-1)

图8 硬币滚动时倾角关于时间的图像(ω3较小)

从图7中还可以发现，当 |ω3|>16.3s-1时,对于相同的 |ω3|，微小章动的周期是相同的，与初始的扰动无关．经检验，章动的周期恰好符合 (34)(35)式推出的结果．

4 在冰面上转动

这里假设冰面是理想光滑的平面，则硬币在运动过程中受到重力以及冰面对它的支持力．由质心系的牛顿第二定律，硬币的质心在水平方向上的运动速度为恒定的vxy．考察同样以vxy运动的参考系，在此参考系中，硬币质心只做竖直方向上的运动，速度和加速度分别为

(38)

(39)

由质心运动定理，硬币在P点受到了向上的支持力FN=-mg+maO，由此可以计算力矩：

(40)

(41)

由于硬币只受到竖直方向的外力，硬币相对于O点的角动量的在ez方向上的分量不变. 设这一分量为b，则

I2ω1cosθ+I1ω3sinθ=b,

(42)

最后，由 (6)(38)式整理得能量守恒方程，设总能量为E，并将 (3)(41)式代入化简，

E-mgrcosθ

(43)

联立 (42)(43)式，消元后可得关于θ的一维运动方程．在解出θ(t) 后，就可以依次代入 (41)(42)式解出φ(t)、ψ(t)．

(44)

(45)

(46)

5 数值模拟

5.1 硬币数据

我们使用的是第五套人民币一元硬币的数据：

半径为r=12.5 mm．厚度为 1.85 mm(忽略不计)．质量为m=6.1 g．计算可得I1=4.8×10-7kg·m2，I2=I1/2=2.4×10-7kg·m2．

5.2 数值模拟方法

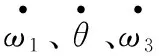
6 总结：

本文采用普通物理的分析方法，推导了硬币在3种环境下的一般运动方程，得到了硬币进行绕圈运动所需满足的条件，并进行了定性分析．在硬币绕圈运动问题中，推导了稳定运动的条件以及硬币做微小章动的周期，进而分析了硬币做定点转动和沿直线滚动的稳定性问题，最后用数值模拟的方法将这两种运动可视化，验证旧结论，并探索新规律．

致谢：本文撰写过程中得到了北京大学物理学院张国辉教授的热情指导，在此表示衷心感谢．