2种奖金制度下的双寡头产量竞争模型的动力学分析

彭建奎， 黎锁平， 杨兆兰， 周小燕

(1.兰州理工大学 电气工程与信息工程学院，甘肃 兰州 730050； 2.兰州文理学院 教育学院，甘肃 兰州 730030)

在经济市场中，企业主通常会雇佣职业代理人来管理公司，但是由于企业主和经理人之间存在利益冲突以及信息不对称的情况，因此企业主为了更好地约束经理人，需要建立激励机制对经理人进行有效的监督.目前，已有很多学者对职业经理人的激励机制进行了研究[1-8].Jansen等[1]提出了纯利润、销售委托、市场份额委托以及相对利润等4种奖金激励机制，并且利用委托游戏对4种激励机制所有可能组合的利润效应进行了研究，结果表明基于相对绩效的奖金制度相对最优；薛超凯等[2]在有限理性的假设下，建立了一种企业主与职业经理人的委托代理模型，但上述研究只是利用静态模型进行研究.为此，学者们相继建立了一些动态的博弈模型来研究系统的演化过程，如Fanti等[3]针对价格竞争和市场份额委托的动态双寡头博弈模型进行全局分析，结果表明在系统演化过程中初始条件尤为重要；Elsadany[4]研究了基于有限理性和企业追求相对利润最大化建立的Cournot模型[5-6]，分析了系统通往混沌的路径.基于上述研究，本文中，笔者利用市场份额和销售委托2种激励机制组合建立了一种动态双寡头产量竞争模型，并通过双参数分岔图、单参数分岔图、最大Lyapunov指数谱分析了系统通过flip分岔进入混沌的复杂的动力学行为，同时通过法里树及吸引盆进一步研究系统的动力学行为和吸引子的共存现象.

1 模型的建立

假设市场上仅存在2家生产同质产品的企业，分别记为企业1和企业2.由于所考虑的是同质产品，因此2家企业具有相同的技术与不变的边际成本，记为c.根据文献[7-8]的研究结果可知，相同质量的产品意味着2家企业生产的产品差异度d=1，假设消费者的效用函数为

(1)

其中：q1和q2分别表示企业1和企业2的产量；a表示市场上产品的最大价格，并且满足a>c>0；b>0表示企业对自己产品价格的敏感性程度，也称为价格敏感性系数[9].

假设消费者的预算约束为

pq1+pq2=M，

(2)

其中p表示产品的价格，M表示消费者对该产品的消费预算.在预算约束下，为了使消费者的效用函数达到最大，由此可得2个企业的逆需求函数

p=a-bQ，

(3)

其中Q=q1+q2,表示市场上2家企业的总产量.根据上述假设，2家企业的利润函数可以表示为

πi=(a-bQ-c)qi，i=1,2.

(4)

在经济市场中，企业主通常雇佣职业经理人并将产量决策权授予职业经理人.为了使经理人给企业带来更多的利益，企业主使用合适的激励合同去激励经理人的工作积极性.在激励合同中，2家企业将经理人的报酬设置为合同工资与合同中签订的奖金之和，2家企业具有相同的合同工资函数，记为si，企业给经理人的合同工资的函数为

si=α+βiπi，i=1,2,

(5)

其中α表示经理人的固定工资，βi表示企业i的经理人为企业做出的贡献值πi每增加一个单位，企业i给予经理人的报酬相应增加βi个单位，i=1,2.

在激励合同中，企业主对经理人表示只有在企业具有正的利润时，企业才履行相应的奖金制度，因此假设2个企业的利润都为正，并且考虑2种奖金形式，企业1根据市场份额的方式确定奖金，然而企业2根据销售委托的方式确定奖金.2家企业的奖金函数如下：

企业1的奖金函数

u1=π1+γq1/Q，

需要指出一点的是，网络舆论的思维方式具有很强的俘获能力，其语言求新求奇、泛娱乐化倾向严重，内容也大多以夺人眼球、追求刺激为要旨，同时它又有着很强的自我构建和寻求扩散的欲望。在构建和传播的过程中，随着各类舆论的合流，其表达方式呈现出强烈的自我肯定性，特别是在舆论发展的后期极易俘获其他网络主体对事物的认知态度。在这种江河汇海似的合流中，网络舆论逐渐逼近某个临界点，开始向现实社会释放能量。可以说，网络舆论的发展过程本身便是网络民主兴起的路径再现。

(6)

其中权重γ表示企业主1基于最大化自己的利益所雇佣的经理人1的委托变量，q1/Q表示市场份额；

企业2的奖金函数

u2=π2+σq2，

(7)

其中σ表示企业主2与经理人2在议价过程中共同选择的激励参数.然而，激励参数σ有正有负，这取决于企业主是激励经理人还是抑制经理人.激励参数σ>0意味着经理人进取心增加，σ<0意味着经理人缺乏积极性.

通过上述假设，给出2家企业经理人的目标函数

将(4)(7)代入上式得

(8)

使得经理人的目标函数最大的一阶条件，也称为边际目标函数，计算如下：

(9)

为了确定经理人随时间变化的行为，建立经理人关于目标函数的信息集十分重要.假设2家企业的经理人都具有有限理性，即经理人对竞争对手的决策和市场需求的信息的了解是有限的，并且假设在t(t∈Z+)时期，2家企业的经理人同时做出决策.因此经理人根据t时期对∂Oi/∂qi(i=1,2)的局部估计来决定t+1时期企业的产量，如果在t时期有∂Oi/∂qi>0，则经理人在t+1时期增加企业的产量，然而如果在t时期有∂Oi/∂qi<0，则经理人在t+1时期减小企业的产量.因此双寡头重复博弈的产量动态调整机制可表示为

(10)

其中ai(qi)是关于qi的正比例函数，描述经理人i(i=1,2)根据边际目标的符号给出的产量变化范围.假设ai(qi)=ψiqi，i=1,2，其中ψi>0为企业的产量调整速度.根据上述假设，动态模型就可以表示为二维非线性差分方程

(11)

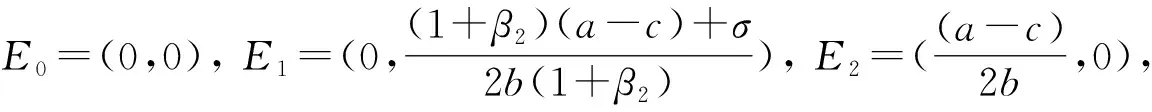
2 Nash均衡点数值分析

通过数值模拟来分析系统Nash均衡点在某一参数变化下的稳定性.固定的参数设置如下：a=0.172 4，b=0.237 0，c=0.022 2，γ=1.637 4，β1=0.213 7，β2=1.855 7，ψ1=2.396 4.激励参数σ与企业2的产量调整速度ψ2的二维分岔图如图1a所示.其中，不同的颜色表示不同周期，黄色区域表示Nash均衡点的稳定区域，绿色、橘色、红色区域依次表示2-周期、3-周期、4-周期，深黑色区域表示混沌区域.拟周期在图1a中用白色表示.由图1a可以看出，在参数平面(σ,ψ2)上，ψ2∈[0,6]时，随着ψ2的增大，系统依次通过黄色、绿色、红色、蓝色区域进入黑色区域，σ∈[0,2]时，随着σ的增大，系统依次通过黑色、蓝色、红色、绿色、黄色区域.为了更直观地分析系统的分岔路径，取ψ2=0.399 4，将σ作为分岔参数，图1a中红色线对应系统的单参数分岔图，如图1b所示.可以看出，随着σ的增加，系统分别经历1-周期、2-周期、4-周期、8-周期等周期后进入混沌状态，然后再由混沌状态分别进入8-周期、4-周期、2-周期和1-周期.由此可知，这一过程是典型的flip分岔与逆flip分岔.图1b还给出了系统在图1a参数下的最大Lyapunov指数谱.可以看出，当最大Lyapunov指数小于0时，系统处于周期状态；当最大Lyapunov指数接近0时，系统处于拟周期状态或者分岔点处；当最大Lyapunov指数大于0时，系统处于混沌状态.由上述分析可知，当σ逐渐增大时，系统由稳定状态逐步进入混沌状态，然后再由混沌状态进入稳定状态，由此可知，经理人应合理选择激励参数使其系统稳定.

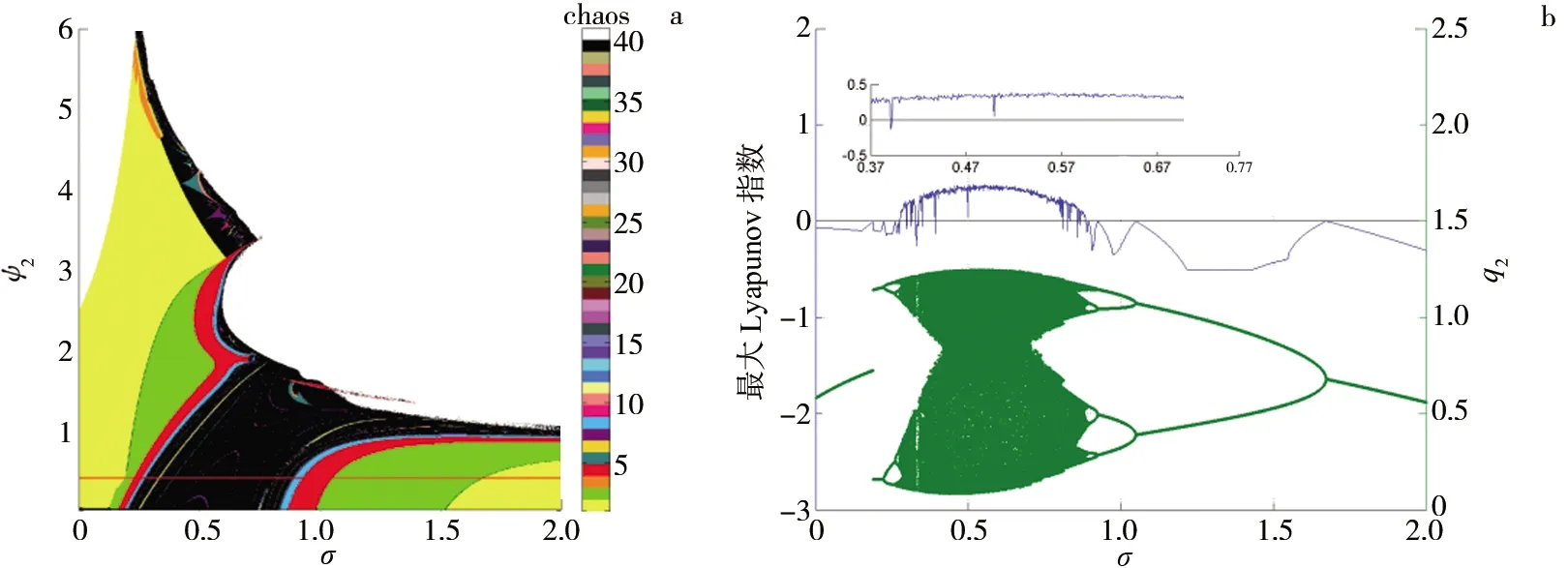
图1 参数平面(σ,ψ2)上的双参数分岔图、单参数分岔图及最大Lyapunov指数谱Fig.1 The Bifurcation Diagram with Two-parameters in Parameters Floor(σ,ψ2)，the Bifurcation Diagram and the Maximal Lyapunov Exponent Spectrum

由图1a还可以看出，在参数平面[0.37,7]×[3.2,4.6]存在复杂的动力学行为.该平面参数的局部放大结果如图2a所示.可以看出，在该区域内展示了类似“舌”的分形序列，并且在这个序列中增加的周期窗口具有自相似性，并且随着σ的增加，“舌”的面积逐渐减小.当取ψ2=3.45时，图2a的单参数分岔图如图2b所示，可以看到单参数分岔图在[0.53,0.63]对应的最大Lyapunov指数位于[-0.05,0.05]，表示拟周期运动.可以看出，系统首先从1-周期进入拟周期，经历周期窗口，最后进入混沌状态.由图1、图2可得，随着σ的增大，商品的市场供应量的波动逐渐变弱，所对应的系统的动力学行为变得越来越简单.这表明当企业的经理人更注重企业收入而非企业利润时，经济市场稳定性会更好，所管理的企业才能在经济市场上长久稳定地发展.

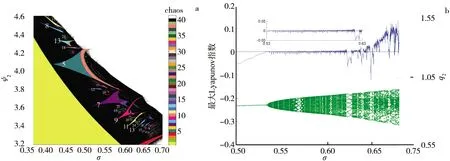
图2 参数平面(σ,ψ2)上的局部双参数分岔图(a)、单参数局部分岔图及最大Lyapunov指数谱(b)Fig.2 The Local Region Bifurcation Diagram with Two-parameters in Parameters Floor(σ,ψ2)(a)，the Local Region Bifurcation Diagram and the Maximal Lyapunov Exponent Spectrum(b)

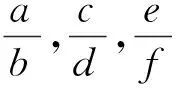
(12)

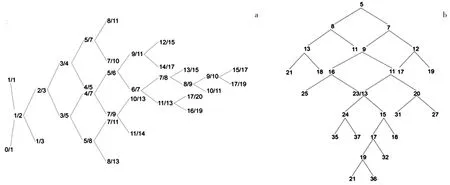
图3 法里树(a)及周期树(b)Fig.3 Farey Tree (a) and Periodic Tree (b)

3 系统多稳态分析

通过数值模拟研究非线性动力系统的过程中，均衡点的稳定性会随着参数的变化而变化.这些变化使得系统出现复杂的动力学现象，如具有分形结构的混沌行为以及吸引子共存等现象[9-11].由于系统的分岔行为使得其解的数量随着参数的变化而发生变化，解的数量的变化导致了系统的吸引子共存现象[12-15].多个吸引子共存意味着系统存在多稳态.接下来通过单参数分岔图以及吸引盆对系统的多稳态进行讨论.由图1a可观察到当ψ2=1.84时，双参数分岔图中的颜色会有部分重叠，这说明此时可能存在吸引子共存.因此在图1参数基础上选定ψ2=1.84，系统对应的单参数分岔图如图4a所示，可以看出，系统经历1-周期、2-周期、4-周期等周期，最后进入混沌状态，并且与图1a相对应.为了更加清楚地观察系统的分岔行为，[0.7,0.8]的单参数分岔图以及最大Lyapunov指数谱如图4b所示，可以观察到系统在σ=0.705 5，0.709 0等分岔点处产生了跳跃现象，这也进一步证明存在吸引子共存现象.以下通过吸引盆进一步解释吸引子共存.

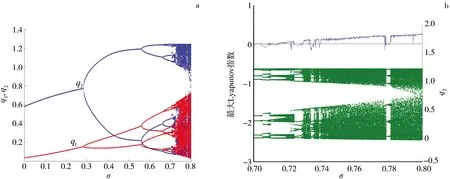
图4 单参数分岔图和最大Lyapunov指数谱Fig.4 The Parameter Bifurcation Diagram and Maximal Lyapunov Exponent Spectrum

通过上述分析说明系统存在多吸引子共存现象，以下通过变化参数来研究吸引子共存以及吸引盆.由图4b可发现，系统吸引子存在跳跃现象，因此给出每个跳跃点处的吸引盆.当σ=0.705 5时，系统的吸引盆如图5a所示，存在2组吸引子，并且都显示为周期点.红色表示16-周期的周期点，其吸引域用白色表示，黑色表示9-周期的周期点，其吸引域用淡蓝色表示，红色区域表示逃逸域.当σ=0.709 0时，如图5b所示，黑色吸引子由9-周期变为24-周期.当σ=0.71时，如图5c所示，红色吸引子的吸引域没有明显变化，黑色吸引子表示为9片混沌吸引子.当σ=0.724时，如图5d所示,黑色吸引子为16-周期的周期点，红色吸引子变为4片混沌吸引子，并且红色吸引子的吸引域逐渐变小，黑色吸引子的吸引域逐渐增大.可以观察到，系统发生了全局分岔，吸引盆不连通.这种吸引子的共存现象说明经理人在竞争过程中有更多的选择.在经济市场中，企业可以据此制定相应的调整策略以实现企业的长期稳定发展，并获得更大的收益.

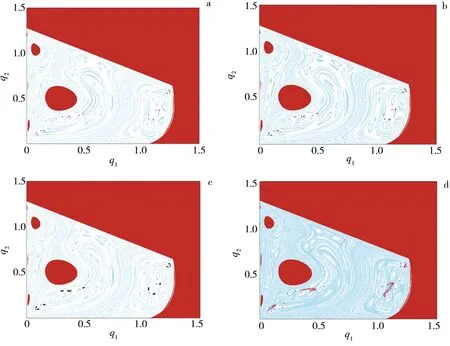
图5 吸引子的演化及吸引盆Fig.5 Attractor Evolution and Attractor Basin

4 结 论

通过建立动态双寡头产量竞争模型对经济市场中常见的职业经理人的奖金激励问题进行研究发现，系统存在4个均衡点.利用数值模拟对系统的Nash均衡点的局部稳定性进行分析发现，系统在参数平面(σ,ψ2)上存在复杂的类似于“舌”的分形结构，通过“法里树”以及“周期树”对这种分形结构进行了研究.通过参数的变化发现，参数的变化对系统的演化过程有着重要的影响，并发现系统存在多稳态情况，同时发现系统可呈现出多种不同形式的吸引子共存现象，此外，吸引盆的分形结构也证明了系统的规律性.这表明在竞争过程中，企业经理人可以有更多的选择，同时这些结论对研究经济系统性质提供了极大的便利.

通常，企业可以在混沌市场中获得一定的利益，但实体经济中的混沌不利于企业的长期稳定发展.因此，对经济市场混沌系统的研究和对未来市场动态的预测就显得尤为重要，同时使得所建立的经济系统模型更加符合实际的经济和市场环境，解决更多的实际问题.以后的研究中还需要对所构建的模型进一步优化、创新，运用分岔与混沌理论进一步分析和预测经济系统的复杂动态行为，为企业做出相应的策略性调整以实现企业的长期稳定发展提供更加准确有效的理论依据.