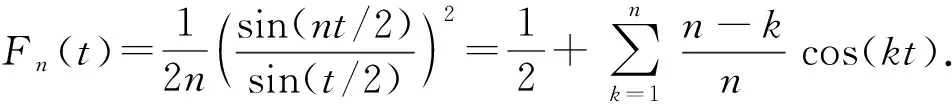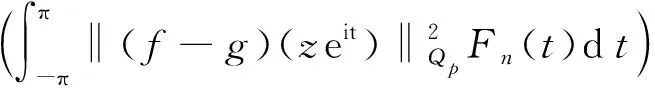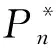Qp空间中的q-光滑模与算子逼近
2022-01-13王志军陈英伟常之魁
王志军, 陈英伟, 常之魁
(河北经贸大学 数学与统计学学院,河北 石家庄 050061)
0 引 言
令g(.,w)为复平面中单位圆盘D上极点在w的Green函数,
g(z,w)=-log|φw(z)|,z,w∈D,
其中φw为D到其上的Möbius变换,
记H(D)为单位圆盘上全纯函数的全体,m(z)为圆盘上lebesgue测度,则称函数f(z)∈H(D)属于Qp空间(0≤p<∞),是指满足
易知[1]‖·‖Qp为半模.若取模为|f(0)|+‖f‖Qp,Qp则为Banach空间.并且Q1为BMOA空间,Q0为Dirichlet空间,当p∈(1,∞)时,Qp为Bloch空间.更多关于BMOA及Qp函数空间的理论,可参考文献[1-2].
Qp空间中的多项式逼近理论近年来已得到一些研究成果[3-5],得到了多项式逼近的正逆定理,即Jackson定理和Bernstein定理等逼近结果.
连续模有多种定义方式,熟知经典全纯光滑模ωr(δ,f,Qp)定义如下
(1)
其中差分为
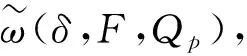
在这点上其延续了实连续模的性质.相比较,经典复连续模对于多项式并不消零.自然会想到作为Hardy空间的极限情况BMOA空间中考虑逼近问题,而BMOA空间可作为Qp空间的特例,故将其纳入Qp空间来统一考虑.
首先在全纯Qp空间中给出一种新的基于差分的q-光滑模及其性质,再由推广的Abel-Poisson平均构造算子获得多项式逼近阶和slice边界光滑性之间的一些内在逼近关系.在Qp中获得基于q-光滑模的Jackson逼近定理.并考虑了de la Valiée Poussin算子的定量最佳逼近.
本文中,符号C表示正的常数,不同的地方值有所不同,但都不依赖于f和n.
1 q-光滑模
对任意f∈H(D),易知均有Taylor展开式
(2)
现在引入一种基于Newdon插值均差的q-光滑模.函数f在各节点zk∈D的插值[8]记为
[z0;f]=f(z0),
…,
易知
另外上述均差还有另一种表达式
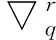
(3)
通过归纳法等直接计算,可推出r阶q-有限差分的一些性质[6]:
a) 另一种表达式
其中Pr,k(q)为Gauss多项式
易知,
Pr,0(q)=1.
b) 递推公式
c) 对n∈N,
d) 积分表示

易知,|z(t1+q(ti-t2)+…+qr-1(tr-1-tr)+qrtr)|≤|z|.

(4)
由上述定义及q-有限差分性质易得,Qp空间中q-光滑模仍具有的典型性质(关于实的情况可参见文献[8]):
(5)
(6)
(7)
其中(5)利用q-有限差分性质(1),(6)可由性质c)得到.
特别地,由(3)和(4)或性质d),易知q-光滑模对代数多项式具有消零性质,

2 Jackson定理
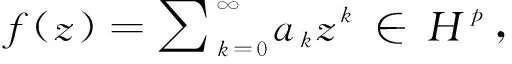
‖f(reiθ)-f(eiθ)‖p≤Cω(1-r,f)p,0 引入推广的Abel-Poisson平均 (8) 其中h=ρeit,0 令h=ρeit,n∈N,α>0,则有 构造积分算子 其中n>r,α>r, 后面定理3中将证明Rn[f](z)与参数p无关,并用作函数f的n次逼近多项式. 广义Jackson核函数为 引理1[8]对于任意的β∈N,存在正常数C(β),使得对任意u=0,1,…,2β-2和k∈N,有 引理2令r,k∈N,则r≤2β-2时, 证由引理1可得 现给出q-光滑模形式的Jackson定理. 定理1设f∈Qp(0≤p<∞)及给定r∈N,α>r,则存在一多项式Rn,其次数n≥r+1,满足 证显然只需证明 由推广的Abel-Poisson平均来构造逼近算子 下面证明Rn(z)=Rn[f](z)=Rn(z;f,r,α)为独立于ρ且为次数至多为n的代数多项式.由f的Taylor展开及 则 h-(n-r+1)h-k(k-1)/2-k(r-k)f(zqk)(1-q)-(1-α)Pr,k(h)= (9) 注意到高斯多项式Pr,k(h)=∑cshs为关于h=ρeit次数至多为k(r-k)的多项式.对t在[-π,π]上积分,并利用留数定理,可知剩下不为0的项满足 -(n-r+1)-k(k-1)/2-k(r-k)+jk+l+s= k(j-r)-(n-r+1)+k(k+1)/2+l+s=0. 再由0≤k≤r,0 为简化,令m=n-r+1并取α>r,有 从而 (10) 特别取η=1,故由(3)可得 不妨取ρ=1-m-1易知 令r≤1+α-2,即α>r,再由积分型Minkowski不等式及引理2,得 定理得证. 对于f∈H(D),引入卷积算子 经由Fejér算子Fk(f)(t)引入de la Vallée Poussin平均算子[12-13] Vn(f)(z)=2F2n(f)(z)-Fn(f)(z). 在Qp空间中该算子可达定量的最佳逼近结果,即说明可构造具体算子在一定程度上达到最佳逼近. 定理2设f∈Qp(D),p>0和n∈N,则Vn(f)(z)次数至多为2n-1的代数多项式,且满足 证算子Vn(f)(z)为次数至多为2n-1的代数多项式[13],由三角函数的积分正交性计算可知 为n次多项式,从而推知算子Vn(f)(z)为次数至多为2n-1的代数多项式. 令f,g∈Qp,p>0,则由函数φ(t)=tp的凸性,可得不等式(a+b)2≤2(a2+b2),对所有的a,b≥0.利用引理3,可得 再由Fn(t)dt为概率测度,故 作为Qp空间的特殊情况,Q1为BMOA空间,故给出有界平均震荡解析函数BMOA的相应逼近结果. 推论1设f∈Q1和n∈N, a) 对给定r∈N,则存在一多项式Rn,其次数n≥r+1,满足 其中常数C独立于n,f; b)Vn(f)(z)次数至多为2n-1的代数多项式,且满足估计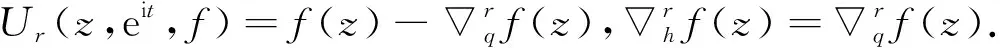



3 de la Vallée Poussin算子逼近