Li2—F体系的基态势能面
2022-01-13李庆玲刘国庆杨晶晶章成文
王 悦, 李庆玲, 刘国庆, 杨晶晶, 章成文
(铜陵学院 电气工程学院,安徽 铜陵 244000)
Li2—F分子属于超碱金属化合物和氟化物,与最外层8电子的稳定结构不同,其最外层共有9个价电子,所以该体系存在弱相互作用,基态电离能很小,有关理论分析有一定困难.
目前,关于Li2—F的基态和激发态势能面的研究报道并不多.Yokoyama等[1]于2000年在气相质谱分析时首次发现了Li2—F自由基,把Li2—F看成是氟-掺杂锂团簇LinFn-1中最简单的一种,采用激光质谱电离方式进行了质谱分析,研究所得Li2—F的电离能为3.78±0.2 eV;2003年,Olivera等[2]用表面电离在热金属表面生成中性原子、分子或者离子的方式,通过研究得出Li2—F分子的电离能也为3.78±0.2 eV;2007年,Velicˇkovic'等[3]用高温电离与Cs+比较的方法得到LinF(n=2~4)几种超价化合物,讨论了它们的质谱,分析了电离能,得到的Li2F分子的电离能为3.8±0.2 eV;2012年,Dustebek等[4]把Li2F也看成是锂-掺杂氟团簇LinF中最简单的一种,采用三倍高热质谱电离方式,改进了之前的质谱分析,得到的Li2F的电离能为4.06±0.2 eV.
理论上,最早是1999年Sengupta等[5]采用MP2-full/6-311(11) G**和单、双迭代(含三重激发微扰校正)耦合簇CCSD(T)计算水平,得出了Li2F的电离能,为3.87 eV;2002年,Haketa等[6]采用6-311+G(d)基组,Mpuer Plesset微拢理论MP2和密度泛函理论B3LYP 2种方法计算出的Li2F的电离能分别为4.47,4.78 eV;2009年,Kris等[7]用CCSD(T)/aug-CVTZ all electrons方法做了更进一步的研究,其算法和基组都比之前的理论计算更复杂,在此基础上,画出了LiF分子的X2A’和A2A’两态势能曲线.近几年,科学家们对Li2F分子研究的兴趣更加浓厚,2015年,Srivastava等[8]利用非线性光学理论,在MP2水平上用Gaussian 09程序6-311++G(d,p)基组对LinF(n=2~5)团簇特性进行了分析,得到的Li2F电离能为3.85 eV,此数据与2000年所得数据的相对误差为1.9 %,与2013年所得数据的相对误差为5.2 %.2016年,Bhowmick等[9]针对基态势能计算比较困难的问题,采用了大基组和显关联多参考组态相互作用MRCI-F12方法分析了Li2F的11A1,13B2等态的势能曲线;2016年,Srivastava等[10]仍采用非线性光学理论、Gaussian09程序,改用大的基组aug-cc-pVTZ和高级别算法二次组态相互作用QCISD算出的Li2F电离能为3.89 eV,此数值与2013年所得数据的相对误差为4.2 %,说明大的基组和高级别算法能较好地改善势能面计算结果.1999年,厦门大学物化研究所Cao等[11]用自洽场VBSCF方法理论计算出了12B2-X2A1第一激发态的活化能,为1.236 1 eV;2007年,吉林大学Wang等[12]详细讨论了Li2F-和Li6F-的基态和低激发态的量子动力学行为.以上研究均未涉及Li2—F分子体系的势能函数表达式,关于Li2—F分子体系的三维势能面的研究也未见报道.
本文中,笔者采用大基组,从头算ab initio方法研究Li2—F体系的相互作用势,得到了三维势能面,可以为Li2—F体系理论研究提供依据.
1 模型的构建
Li2—F聚合体属于三原子分子体系,可以采用Jacobi坐标系(r,R,θ),如图1所示.把Li—Li固定于x轴,坐标原点处于Li—Li中点位置,r表示Li—Li间距,R表示原点到F原子的距离,F原子与Li—Li中心连线(x轴)夹角为θ,由于F与Li—Li靠得太近会出现相互排斥,选取中心键函数Bq,并放置在原点到F原子的连线中点.通过变换角度θ(从0 °~90 °取30 °为间隔),R=0.2a0~13a0,对于非势阱区域取点较稀疏,接近势阱区域取点密集.在G09程序包中[13]先进行预算,发现在θ=90 °出现势阱,所以在势阱附近计算时取ΔR=0.1a0,在弱相互作用的长程区域取ΔR=1a0,三维空间中一共计算了456个位置的势能值.
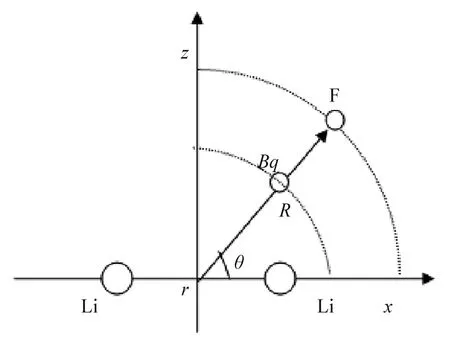
图1 Li2—F体系的计算坐标Fig.1 Coordinates Used in the Fitting Formula
2 计算方法
计算中,选取短程和势阱区相对误差比较小的aug-cc-pVQZ/F,aug-cc-pCVTZ/Li作为基组,进行三维势能面扫描,采用FCP(full couterpoise)方法[14]消除.在超分子近似中,势能为相应能量的差值
V(R,θ)=EF-Li2[BessF+BessLi—Li]-EF[BessF+BessLi—Li]-ELi2[BessF+BessLi—Li],
(1)
其中Bess表示基组.采用最小二乘法拟合方法将从头算得到的空间势能值描述一个解析势能函数
V(q,R,θ)=Vsh(q,R,θ)+Vas(q,R,θ).
(2)
短程部分用Vsh(q,R,θ)表示,长程部分用Vas(q,R,θ)表示[15].短程部分的函数形式为
Vsh(q,R,θ)=G(q,R,θ)e[D(q,θ)-B(q,θ)R].
(3)
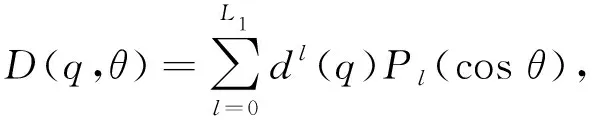
(4)
(5)
(6)
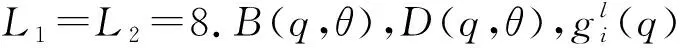
长程区域函数形式为
(7)
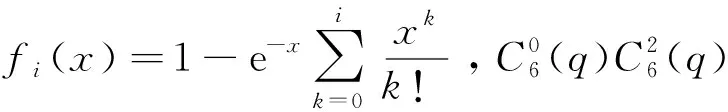
3 结果分析
按照间隔30 °变化角度描绘出不同角度的势阱位置.图2给出了0 °,30 °,60 °,90 °的势能曲线.对比这几条曲线可得,随着角度的增大势能越来越向短程靠近,势阱也越来越大,在60 °出现了鞍点.其中0 °对应倒“T”型结构,RLi—Li=5.6a0时,势阱的阱深约为-0.18 cm-1,而90 °对应线型结构,RLi—Li=2a0时,势阱深度约为-0.23 cm-1.可以看出,Li2—F体系势能面上势阱相对比较浅,这说明Li2—F体系相互作用势比较弱.
经过拟合得出了平衡位置Li2—F体系的二维势能面,如图3所示.可见,图3与图2是吻合的,整个势能曲线在总体上呈现出弱的相互作用,势能阱比较浅,当F靠近Li2分子时出现明显的排斥,当F距离Li2分子比较远时,势能面以各向同性为主.
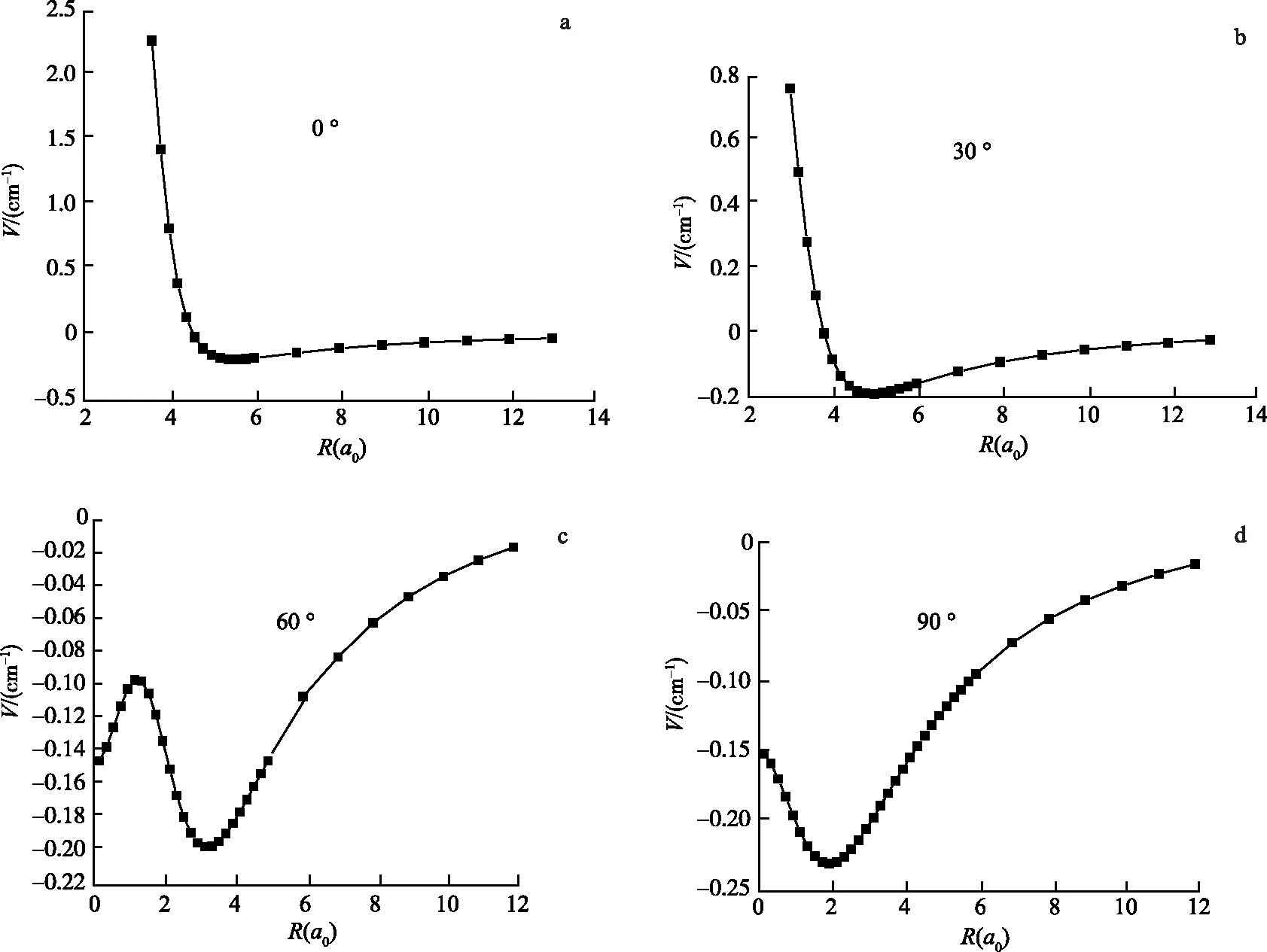
图2 Li2—F体系各不同角度基态势能的对比结果Fig.2 Orientational Features of the PES of Li2—F
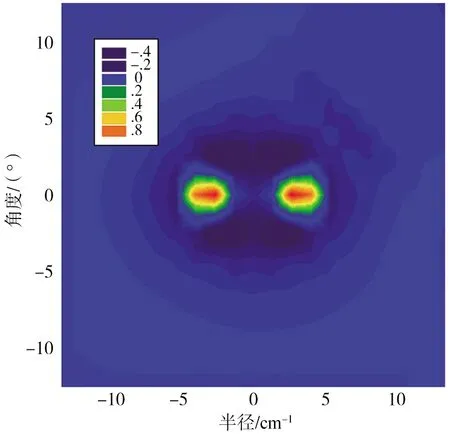
图3 Li2—F体系基态二维势能面Fig.3 Contour Plots of the Potential for Li2—F Complex at r=re Contours Are Labeled
图4为0≤R≤10a0三维空间势能图.可以清晰地看到势阱位置,势能面整体上呈现出弱的相互作用.在长程区域随着R的增大电子间因为关联产生的范德瓦尔斯吸引作用逐渐增强,所以相互作用的吸引力占主导,排斥作用逐渐减弱.在短程区域随着R的减小,由于F原子受到的Li—Li双原子分子形成电子云的排斥作用增加,势能面呈现出很明显的排斥势.因此在Li—Li双原子与F单原子共同作用下,整个三维势能面形成了长程弱吸引短程强排斥和浅势阱的特性.
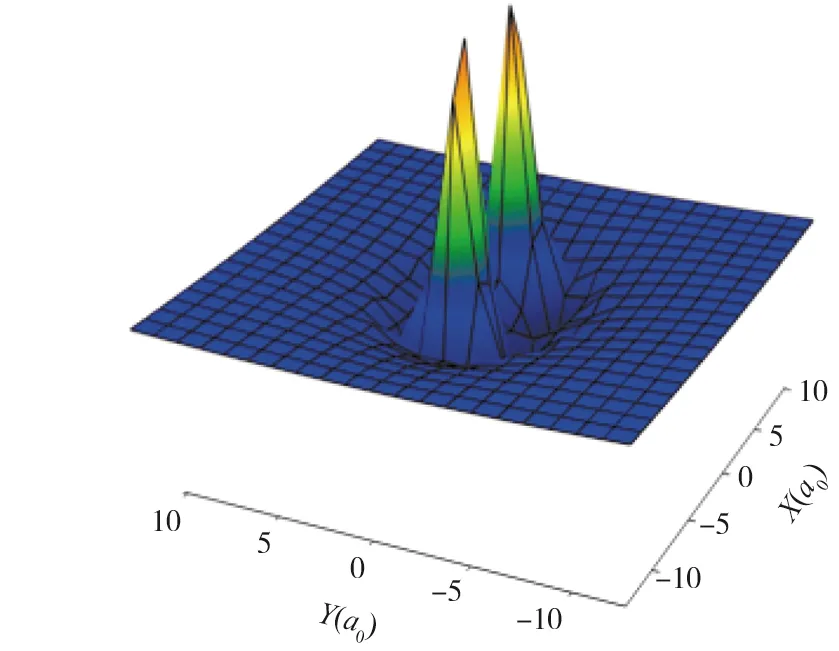
图4 Li2—F体系三维势能图Fig.4 The Close Shot for the Three-dimensional PES for Li2—F
4 总 结
选用大基组,采用单双耦合CCSD(T)方法,计算了Li2—F聚合体基态的全程势能面;通过最小二乘拟合的方法绘制了该体系的二维、三维势能图,发现势能面上有2个比较浅的势阱,分别对应90 °线型结构(RLi—Li=2a0时,势阱深度约为-0.23 cm-1)和0 °倒“T”型结构(RLi-Li=5.6a0时,势阱深度约为-0.18 cm-1).所得结果可以为Li2—F体系的研究提供理论基础.
