列车循环荷载下交叠隧道结构疲劳寿命预测分析

陈长江 李琪睿 田志尧

(1.中铁第六勘察设计院集团有限公司,300308,天津；2.同济大学道路与交通工程教育部重点实验室,201804,上海；3.上海轨道交通基础设施耐久性与系统安全重点实验室,201804,上海∥第一作者,高级工程师)

随着城市轨道交通建设的发展，上下线路交叠隧道工点与日俱增。在近距离交叠隧道中，列车运行产生的振动荷载具有叠加放大效应，会使隧道结构疲劳损伤加剧，进而影响服役期限[1]。

既有研究表明，在列车荷载循环作用下，与接头螺栓相比，隧道管片结构的疲劳寿命更低[2]。因此，本文更关注隧道混凝土结构的疲劳寿命。目前，针对列车荷载下交叠隧道结构动力响应的研究多基于双孔交叠隧道，针对隧道结构疲劳寿命的研究多基于单线隧道。文献[3]研究了近距离立体双孔交叉隧道列车运营期间振动对隧道结构的影响；文献[4]探讨了高速铁路单线隧道衬砌结构在列车荷载作用下的疲劳寿命和破坏机理。较多文献分析了双孔交叠隧道的动力响应或单线隧道的疲劳寿命，但尚未有对于四孔交叠隧道疲劳寿命的研究。考虑到四孔交叠隧道结构振动激励放大效应更为复杂，有必要对其疲劳寿命进行预测分析。

本研究以南京地铁某双线四孔交叠隧道线路项目(以下称为“目标线路”)为研究对象，基于Miner疲劳损伤线性累积准则(以下简为“Miner准则”)，采用FE-SAFE疲劳寿命计算软件，建立交叠隧道-土体系统动力计算模型，探讨软土地区四孔交叠隧道在列车循环动荷载作用下的振动放大效应，预测交叠隧道结构疲劳寿命，对相关地区近距交叠隧道结构长期性能保障技术具有重要借鉴意义。

1 隧道-土体结构疲劳寿命计算原理

1.1 损伤理论

文献[5]指出，在随机疲劳荷载作用及四周疲劳区范围内，结构疲劳寿命分析采用Miner准则可准确地满足工程需求[5]。假设ni为结构经历的应力循环次数N为结构发生破坏时的应力循环次数，则Miner准则认为,在不同应力水平S的循环荷载作用下，结构产生的累积损伤为ni/N，当线性累加得到的损伤总和达到1时，就认为结构已经疲劳失效。可见，结构不发生疲劳破坏应满足：

(1)

1.2 疲劳寿命计算方法

FE-SAFE软件是进行结构疲劳耐久性分析的专用软件。在隧道结构疲劳寿命预测时，先开展ABAQUS动力有限元分析计算结构动力响应，与Miner准则相结合，再将其嵌入FE-SAFE软件分析，预测盾构隧道不同部位的结构疲劳寿命。具体计算过程见图1。

图1 疲劳寿命计算流程图

目标项目的交叠隧道工点处于富水软土地区。考虑最大应力水平参数与最小应力水平参数，在潮湿环境下通过混凝土典型疲劳试验可得疲劳寿命曲线。本文以该曲线来拟合目标项目的混凝土材料疲劳S-N曲线[6]：

lgN=16.67-16.76Stmax+5.17Stmin

(2)

式中：

Stmax——最大应力水平参数，Stmax=σmax/fc；

Stmin——最小应力水平参数，Stmin=σmin/fc。

其中，σmax、σmin分别为最大主应力及最小主应力，可由后续有限元计算得到；fc为混凝土材料抗拉强度。

南京地铁运营时间大致为06:00—23:00，共17 h，按发车间隔6 min计算，每天发车170列，一年发车62 050列。由于南京地铁列车为6节编组，故1年振次Na=372 300次。据此计算疲劳寿命对数值，进而计算疲劳寿命年限：

(3)

列车荷载作用下的隧道结构疲劳寿命振次计算可采用按列车对数计算[7]、按列车编组数计算[8]及按轮轴计算[5]三种方法，目前学术界并无统一。本文采用按列车编组计算的方法，并引入疲劳寿命折减系数η作为定量分析交叠区振动放大效应对疲劳寿命折减影响的评价指标。

2 隧道-土体动力耦合计算模型

2.1 工程概况

A线(下方隧道)交叠B线(上方隧道)节点如图2所示。两线最小净距约为3.5 m，交叉区段长宽均约为20 m，场地潜水位埋深约为0.5 m。

图2 交叠节点工程概况

A线与B线均采用南京地铁标准制式混凝土管片，外径为6 200 mm，内径为5 500 mm。管片厚度均为350 mm，环宽为1.2 m，纵缝设置凹凸榫，纵向采用全旋转错缝拼装。两线均采用整体式浇筑道床。A线与B线均采用6节编组的A型地铁列车，最高运行速度为80 km/h。

2.2 隧道-地层三维动力数值计算模型

采用有限元软件ABAQUS建立轨道-隧道-土层的三维动力计算模型，如图3所示。为消除边界效应，提高计算精度，模型长度取隧道直径的8～10倍，则模型尺寸为100 m×100 m×50 m。为消除低通效应，模型中，重点研究区域的网格尺寸为0.25 m×0.25 m，远场网格尺寸为2.0 m×2.0 m，二者之间网格尺寸逐渐过渡。

图3 交叠隧道有限元模型

2.3 列车荷载模拟

本文通过在扣件对应位置施加随时间变化的集中力的方式来模拟列车运行。扣件集中力作用位置设置为距模型边界10 m，以避免边界效应。扣件集中力时程曲线由车辆-轨道垂直耦合动力学模型获得，如图4所示。一系悬挂系统、二系悬挂系统及轨道的扣件系统用并联的线性弹簧和粘性阻尼模拟。钢轨采用离散支承的无限长欧拉梁模拟。车轮与钢轨间垂向接触采用赫兹非线性接触。

图4 地铁列车运行扣件力

为模拟双线四孔交叠隧道运行的最不利情况，模型中4列列车同时由模型边界对向驶向交叠区域。

2.4 计算参数

隧道、整体式道床及地层均以实体单元建模，以等效刚度法对隧道结构管片间接头作用下的刚度折减，并合并参数相近的土层。交叠节点的地层-结构模型材料参数如表1所示。

表1 交叠隧道模型材料参数表

采用瑞利阻尼来反映振动在土层材料中的能量耗散。选取地铁运行引起地表响应的频率范围上下限分别为wi=5 Hz、wk=100 Hz，令阻尼比ξ=0.05，计算得瑞利阻尼系数α=2.991 993，β=1.515 761×10-4[9]。

2.5 工况设计

在影响四孔交叠隧道疲劳寿命的因素中,列车运行速度及交叠隧道净距尤为显著。保持双线四孔交叠隧道模型其他参数不变，在交叠隧道净距为3.5 m时将列车运行速度依次取20 km/h、40 km/h及80 km/h，并在速度为60 km/h时将交叠隧道净距依次取2.0 m、6.0 m及12.0 m，建立有限元模型，以研究列车运行速度及交叠隧道净距对四孔交叠隧道结构疲劳寿命的影响。具体计算工况见表2。

表2 计算工况

3 计算结果及分析

3.1 最小疲劳寿命断面

通过ABAQUS有限元软件计算测点的动应力，研究双线四孔交叠隧道结构交叠区动力放大效应和疲劳寿命。疲劳寿命最小处即为主应力最大处。按照表2中原始工况相关参数建立双线四孔交叠隧道有限元模型，计算列车运行时程内4条隧道的动应力变化值。计算结果如图5所示。由图5可见，在列车运行时程内，隧道结构最大主应力出现在4列列车交汇时的上方隧道拱底a点位置。图6中的a点最大主应力时程曲线变化情况也验证了这一点。此外，在上方隧道拱底设置b、c、d、e、f、g等测点以进一步研究动力放大效应影响范围。

图5 观测测点平面图(最大主应力出现处)

图6 a点最大主应力时程曲线

将a点的隧道结构最大主应力作为σmax代入式(2)，并嵌入FE-SAFE软件进行耦合计算，得到a点盾构隧道疲劳寿命对数云图，如图7所示。

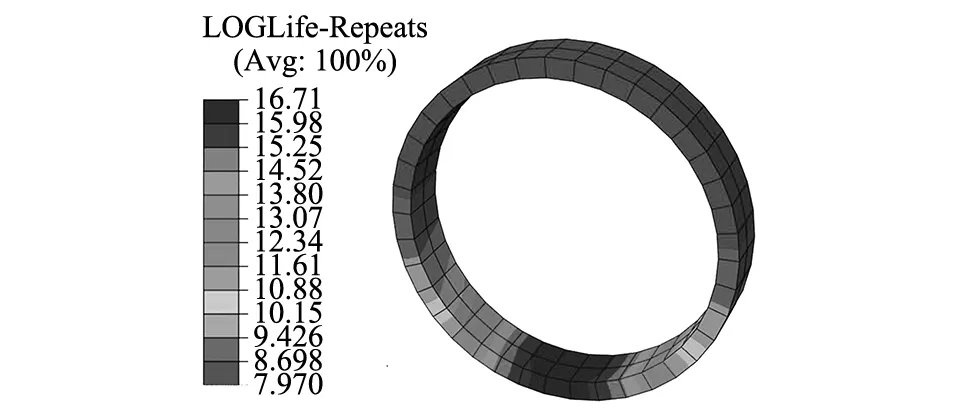
图7 a点隧道结构疲劳寿命对数云图

由疲劳寿命对数计算值及式(3)计算疲劳寿命年限。经计算，双线四孔交叠隧道在原始工况下，疲劳寿命薄弱位置为四孔交叠隧道中心处上方隧道拱底a点处，且疲劳寿命为251年。

3.2 动力放大效应影响范围

为分析交叠隧道动力放大效应影响范围，计算b、c、d、e、f、g测点的最小疲劳寿命，并绘制图8。其中，b点与a点间范围为双线四孔交叠隧道的交叠区。

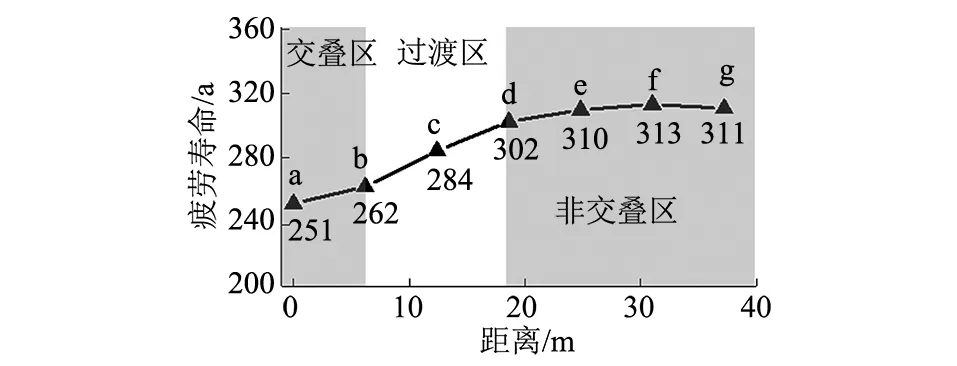
图8 各测点的疲劳寿命

根据计算结果，在距离双线四孔交叠隧道交叠区2D以上的区域(d、e、f、g测点)疲劳寿命变化平缓，说明动力放大效应明显衰退，对结构疲劳寿命影响已不大，故将距a点3D以上区域定义为非交叠区，并将距a点D～3D之间区域定义为过渡区。

考虑到影响疲劳寿命的因素众多，计算误差难以避免，基于归一化的思想，本文定义疲劳寿命折

减系数η为交叠区最短疲劳寿命与非交叠区疲劳寿命的比值。η不仅能较直观地反映交叠隧道动力放大效应对隧道结构疲劳寿命的影响程度，还能直观地指导普通线路隧道与交叠隧道区域长期维养成本的投入比例。例如，普通线路隧道服役寿命设计为100年，交叠隧道区域可按照服役寿命为η×100的标准展开维养。在此基础上，进一步探讨列车运行速度与交叠隧道净距对η的影响。

3.3 列车运行速度对η的影响

保持双线四孔交叠隧道轨道-隧道-土层模型其他参数不变，依次取列车运行速度为20 km/h、40 km/h、80 km/h，计算交叠隧道在不同列车运行速度下的疲劳寿命，进而得出η与列车运行速度的关系，如图9所示。

图9 列车运行速度与η的关系

由图9可见：列车运行速度对交叠隧道疲劳寿命有较大影响；列车运行速度越小，η越大，说明交叠动力放大引起的结构疲劳衰减效应越小。当列车运行速度仅为20 km/h时，η仍达0.92，说明即使列车速度较低(在车站端头处)，动力放大效应也对交叠隧道疲劳寿命有一定影响。当地铁列车运行速度达到80 km/h时，η=0.80，即交叠区疲劳寿命约为非交叠区的0.8倍，说明动力放大效应对交叠隧道疲劳寿命有较明显影响。

3.4 交叠隧道净距对η的影响

保持交叠隧道模型其他参数不变，依次取交叠隧道净距为2.0 m、6.0 m及12.0 m，计算交叠隧道在不同净距下的疲劳寿命，得出η与交叠隧道净距的关系，如图10所示。

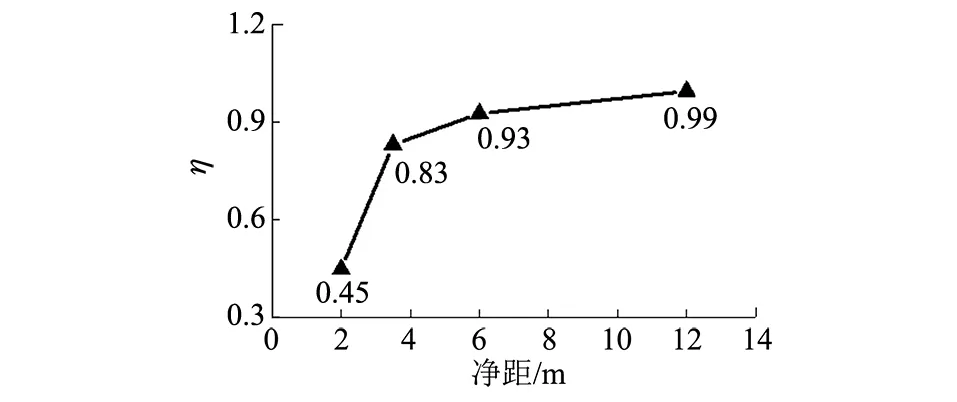
图10 交叠隧道净距-疲劳寿命折减系数图

由图10可见：交叠隧道净距对交叠隧道疲劳寿命有较大影响；交叠隧道净距越大，η越大，说明交叠动力放大引起的结构疲劳衰减效应越小；当双线四孔交叠隧道净距达到6.0 m(约1D)时，η发展趋于收敛；当双线四孔交叠隧道净距达到12.0 m(约2D)时，η高达0.99，说明此时交叠区域隧道结构疲劳寿命基本不受交叠隧道动力放大效应的影响。

4 结论

1) 四孔交叠隧道具有动力放大效应。疲劳寿命薄弱点为四孔交叠隧道中心处。

2) 距离四孔交叠隧道交叠区2倍隧道直径以外的区域可视为非交叠区。非交叠区内动力放大效应衰减明显，对结构疲劳寿命影响已不大。

3) 定义交叠区最短疲劳寿命与非交叠区疲劳寿命的比值为疲劳寿命折减系数η。η能够较为直观地指导普通线路隧道与交叠隧道区域长期维养成本的投入比例。

4)η与列车运行速度的关系为:列车速度越小，η越大(即交叠动力放大引起的结构疲劳衰减效应越小);列车运行速度即使较低，动力放大效应也仍对交叠隧道疲劳寿命有一定影响。

5)η与双线四孔交叠隧道净距的关系为:四孔交叠隧道净距越大，η越大(即交叠动力放大引起的结构疲劳衰减效应越小);交叠区域隧道结构疲劳寿命基本不受动力放大效应的影响。