Low-rank constrained weighted discriminative regression for multi-view feature learning

Chao Zhang | Huaxiong Li

Department of Control and Systems Engineering,Nanjing University,Nanjing, 210093,China

Abstract In recent years,multi-view learning has attracted much attention in the fields of data mining,knowledge discovery and machine learning, and been widely used in classification, clustering and information retrieval,and so forth.A new supervised feature learning method for multi-view data,called low-rank constrained weighted discriminative regression(LWDR),is proposed.Different from previous methods handling each view separately,LWDR learns a discriminative projection matrix by fully exploiting the complementary information among all views from a unified perspective. Based on least squares regression model, the highdimensional multi-view data is mapped into a common subspace,in which different views have different weights in projection. The weights are adaptively updated to estimate the roles of all views. To improve the intra-class similarity of learned features, a low-rank constraint is designed and imposed on the multi-view features of each class,which improves the feature discrimination. An iterative optimization algorithm is designed to solve the LWDR model efficiently. Experiments on four popular datasets, including Handwritten,Caltech101,PIE and AwA,demonstrate the effectiveness of the proposed method.

1 | INTRODUCTION

Owing to the rapid growth of multimedia data, multi-view learning aroused much interests of researchers from data mining, knowledge discovery and machine learning areas in recent years [1–8]. In real world, one object can be described by different kinds of data or from different views.For example,a news can be expressed by texts, audios and videos. One person can be identified by the face, fingerprint and DNA information. Although these features may be heterogeneous and very different, they naturally reflect some inherent structures or characteristics of the object. Compared with single view data, multi-view data contains more underlying information. How to effectively and efficiently exploit the correlative yet complementary information among diverse views is an important research topic for multi-view learning [9].

Many researchers tried to develop effective information fusion techniques for multi-view learning, including unsupervised [9], semi-supervised [10] and supervised [11, 12]. Some researchers proposed multi-view learning methods by cotraining[13,14]and co-regularization[15,16].However,these methods neglect the problem caused by the high dimension of multi-view data. Canonical correlation analysis (CCA) is a classical unsupervised multi-view subspace learning method,which seeks a low dimensional feature space by maximizing the correlation between different views [9]. However, CCA can only deal with two views which limits its further application on more complex data.Luo et al.proposed a tensor CCA method,which extended original CCA for multiple views[17].To make use of the label information for better classification performance, Kan et al. proposed a multi-view discriminant analysis(MvDA) method by maximizing the inter-class distance and minimizing the intra-class distance from both inter-view and intra-view [11]. MvDA can be regarded as the extension of linear discriminant analysis (LDA) on multi-view data. These methods mentioned above can be categorized into subspace learning based methods,which assume that different views can be generated from a common latent feature subspace.

Regression-based method is one of the most popular methods in machine learning [18–22], and it provides another effective and efficient way for multi-view feature learning[23].Specifically,regression-based methods seek a linear mapping by transforming data to fit the label matrix.Zheng et al.extended low-rank regression model for single view data to multi-view fully low-rank regression (FLR), in which multiple projection matrices were learned and the final classification was performed by majority voting [23]. However, FLR does not consider the differences among all views.Yang et al.proposed an adaptiveweighting discriminative regression(ADR)by learning a unified transform matrix for multi-view classification [24]. ADR introduces an adjustment matrix to enlarge the distance between different classes which improves the model robustness to some extent. However, the intra-class compactness is destroyed in ADR,which is also important for pattern analysis.In[25],the authors incorporated feature selection into linear regression model by l2,1-norm regularization.Wen et al.adopted a graphregularized matrix factorization model to handle the multi-view clustering problem with incomplete views[7].

In this article,we propose a multi-view low-rank weighted discriminative regression(LWDR)method for feature learning.LWDR learns a common feature subspace across all views.Adaptive weights learning mechanism is adopted to automatically learn different views and the important views containing more discriminative information is enforced to contribute more to subspace learning. To improve the intra-class similarity,a class-wise low-rank constraint is imposed on the multiview features.Besides,a flexible error term based on l2,1-norm is introduced to relax the label matrix. Experiments on four datasets demonstrate that LWDR outperforms previous single view feature learning methods and related multi-view learning methods.

The rest of this paperarticle is organized as follows.In Section 2,we briefly review the related works about linear regression methods for multi-view learning. Section 3 introduces the formulation of our proposed method and the optimization algorithm in detail.Section 4 reports the experimental results and analysis.Section 5 concludes this article.

2 | RELATED WORKS

where Wkis the projection matrix of the k-th view. It can be observed that Equation (2) is equivalent to simply concatenating multi-view features into one single view feature and performing traditional linear regression on it.Such operation is not physically meaningful and treats all views equally.However,different views usually have different characteristics and contribute differently to pattern analysis. For example, to identify a person, the face appearance is more important than voice. Thus, adaptive weights learning strategy is introduced into multi-view linear regression model by weighting different views, which can be generally described as follows.

where δkis the weight of the k-th view. The first term and constraints force the model to learn optimal weight for each view automatically.However,in Equation(3),the latent multiview features are directly regressed to approximate the binary label matrix Y, which may be too strict and is not appropriate as the regression target. To improve the model robustness, in[24], the authors relaxed the label matrix and proposed the following auto-weighted discriminative regression model for multi-view classification (ADR):

where b ∈Rcis a bias vector and M is a non-negative matrix.By introducing the adjustment matrix M,the one-zero labelvectory=[1,0,…,0]Tisrelaxedto[1+Mij,0,…,0]T(Mij≥0), where Mijis the corresponding element in M. By introducing non-negative matrix M, Equation(4)uses the ϵ-draggings technique to enlarge the distances between true and false classes and improve the model robustness. Such label relaxation strategy is widely used in other regression-based methods [26, 27].

3 | PROPOSED METHOD

In this section, we present our proposed LWDR method and the optimization algorithm in detail, then we will make some discussions on the computational complexity of LWDR.

3.1 | Formulation

From Section 2, although the ϵ-dragging technique used in ADR [24] enlarges the distance between different classes or inter-class separability to some extent,the same class may have different labels after relaxation(i.e.Y+Y ⊙M)because of the dynamic of M. Thus, the intra-class similarity cannot be guaranteed in ADR and two samples from same class may be projected distant from each other.Both inter-class separability and intra-class similarity are important for good classification performance. In low-rank representation (LRR) [28–30], a set of instances are generally drawn from a union of multiple subspaces, and the instances of each subspace are regarded from the same class, which illustrates that the instances from the same class should locate in the same subspace and the data matrix of each class should be low-rank.Inspired by this issue,we propose the following low-rank constrained adaptive weighted discriminative regression(LWDR)model to improve the intra-class similarity of learned multi-view features:

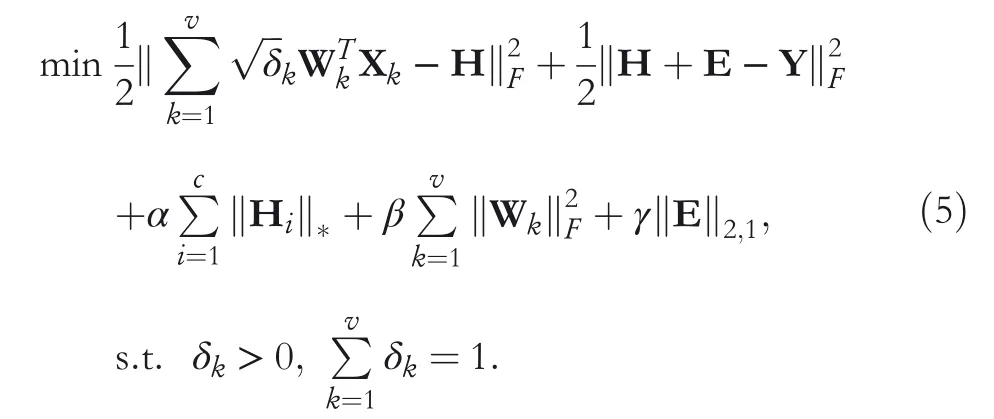
3.2 | Optimization

To make the variables separable in Equation(5),we introduce an auxiliary variable T and rewrite the original problem as follows:

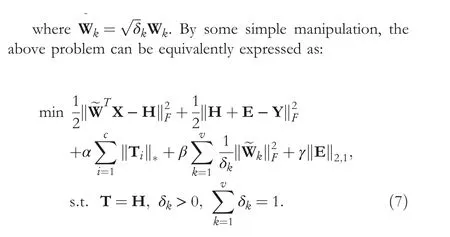
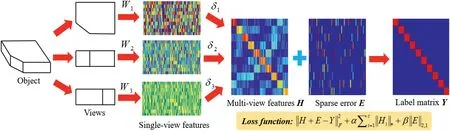
FIGURE 1 The overall framework of LWDR model for multi-view feature learning.LWDR adaptively learns a projection matrix and a weight for each view.Then the multi-view features H can be obtained by integrating the single-view features using learned weights.Label matrix Y is used as regression target to guide the feature learning in a supervised way,and a sparse error matrix E is introduced to compensate the regression error.To improve the intra-class compactness of multi-view features, a class-wise low-rank constraint on multi-view features is incorporated into LWDR

where ～W=[～W1; ～W2;…; ～Wv],X=[X1;X2;…;Xv]. To solve, Equation (7) is equivalent to minimize its augmented Lagrange function Lθdefined as:

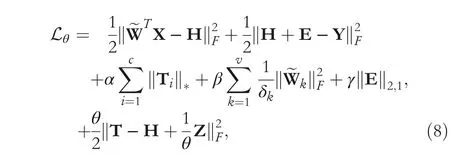
where θ ＞0 is a penalty factor and Z is the augmented Lagrange multiplier. We adopt the iterative strategy to minimize it, in which a sequence of sub-problems with respect to each unknown variable are solved respectively[31–33]. In specific, it contains following six steps in each iteration.

where Qiis the i-th row of matrix Q.

According to Theorem 1, we can get the solution to Equation (14):

(4) Update T with other variables fixed by solving the following optimization problem:

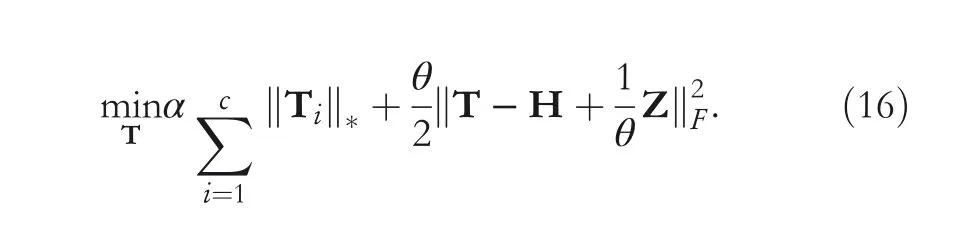
Equation (14) can be solved by the following theorem.

Algorithm 1 Iterative algorithm for solving LWDR Input: Multi-view data ｛Xk｝vk=1, parameters α, β,γ.Output: Projection matrix ～W.1: Initialization: H = Y, E = W = Z = 0,θ = 10-3, θmax = 105, ϵ = 10-6.2: t = 0.3: while not converged do.4: Update ～W by Equation (11);5: Update H by Equation (13);6: Update E by Equation (15);7: Update Ti by Equation (18) and update T = [T1, …, Tc];8: Update ｛δk｝v k=1 by Equation (21);9: Update Z and θ by Equation (22);10: Check convergence conditions:‖Wt+1-Wt‖2F+ ‖Et+1-Et ‖2F +‖Ht+1-Tt+1‖2F <ϵ;11: t ←t + 1;12: end While

It can be transformedto solve each Tirespectively.

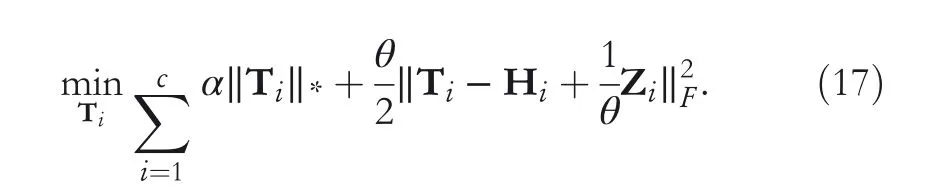
In this article,θmax=106and ρ=1.1.By performing steps(1)–(6) iteratively, the original loss function can be minimized until convergence or reaching the maximum iterations. Algorithm 1 summarizes the iterative algorithm for solving LWDR model in detail.

3.3 | Computational complexity analysis

3.4 | Connections to other methods

· Connections to FLR [23]: Similar to our proposed LWDR,FLR also adopts regression model for multi-view feature learning. FLR learns a projection matrix for each view with low-rank constraint,which is helpful to explore the low-rank structure of data.However,FLR treats all views equally and ignores the fact that different views have different roles for pattern analysis, which may degrade the classification performance. Differently, our proposed LWDR adaptively learns the weights of all views and enforces those informative views to contribute more to feature learning. Thus,the proposed method can achieve better performance than FLR, which will be demonstrated in experiments.· Connections to ADR [24]: ADR learns a weighted multiview regression model for multi-view feature learning,which considers the different weights of different views.To avoid a rigid regression target,ADR utilizes the relaxed label matrix for regression as presented in Equation(4),which is beneficial to enlarge the margins of samples from different classes.However,according to[34],the margins of samples from the same class may be also enlarged, and the discriminative power of projection matrix will be compromised. To address this problem, LWDR introduces the class-wise low-rank constraint, which enforces the transformed samples of the same class to have the same structure. In this way, the margins of the transformed samples from the same class will be reduced and the intra-class compactness can be improved. Therefore, the proposed method has the potential to perform better than ADR.

4 | EXPERIMENTS

In this section, we conduct the experiments on Handwritten[36], Caltech101 [37], PIE [38] and AwA [39] datasets to validate the effectiveness of proposed LWDR, compared with single view and related multi-view learning methods.

FIGURE 2 Some typical images from Handwritten, PIE and Caltech101 datasets from top to bottom (images of AwA dataset are unavailable due to the copyright problem)

4.1 | Datasets

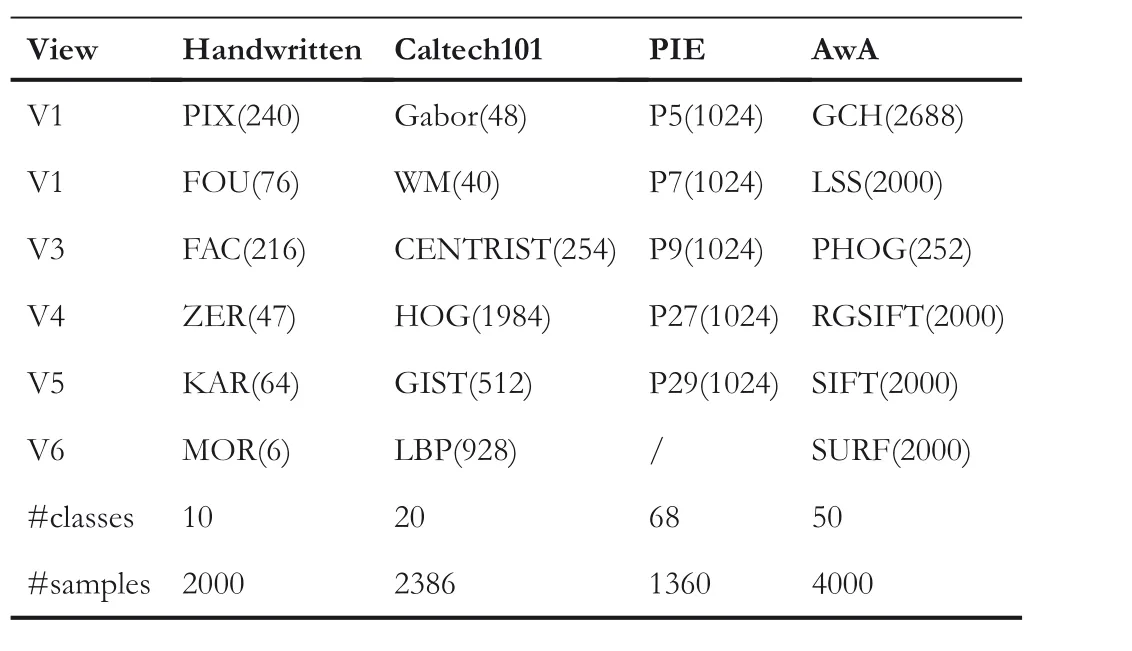
Handwritten dataset contains total 2000 images about 10 number (i.e. 0–9) with 200 images per subject. It contains six feature views, including Pixel Averages (PIX), Fourier Coefficients(FOU),Profile Correlations(FAC),Zernike Moment(ZER), Karhunen-Loeve Coefficients (KAR) and Morphological (MOR) features.

Caltech101 dataset contains 9146 images of 101 different subjects. In our experiments, total 2386 images of 20 classes are used.These images have six feature views,including Gabor,Wavelet Moments (WM), CENTRIST, HOG, GIST and LBP features.

The whole PIE dataset consists of over 40,000 face images of 68 individuals, collected under different pose, illumination and expression conditions.Total 1360 images of 68 individuals are used in our experiments,which contains five different facial poses. The five poses are used as five different views.

AwA dataset contains 30,475 images of 50 kinds of animals.In our experiment,4000 images with 80 images per class are used. AwA dataset contains six feature views, including Global Color Histogram (GCH), Local Self-Similarity (LSS),Pyramid HOG (PHOG), RGSIFT, SIFT and SURF features.

Figure 2 shows some samples images used in our experiments.Table 1 presents the views,feature dimensions,number of classes and samples of these datasets.

4.2 | Experimental setup

For Handwritten and Caltech101 dataset, we randomly select 10 images per subject for training and the rest for testing. For PIE, five face images per person are randomly chosen for training. For AwA, the training size of each class is 20.

We compare our proposed LWDR with single view and multi-view approaches. For single view method, each view is handled separately. LDA is performed on each view for feature learning [40]. The reduced dimension of LDA is c - 1. For multi-view methods, all views are simply concatenated and LDA is used for feature extraction, that is, LDA(all). Also, we concatenate the top three views and then perform LDA, that is, LDA (top three). The top three views are selected based on the performance of single view method.Multi-view methods FLR [23] and ADR [24] are performed for comparison. The parameter settings of FLR and ADR are followed the author's suggestions. Nearest neighbour with cosine distance is used for classification. We repeat the experiments 20 times by randomly sampling data partitions and report the experimental results by the mean recognition rate with standard deviation.

TA B L E 1 Descriptions of four datasets used in our experiments

4.3 | Experimental results

4.3.1 | Classification accuracy comparison

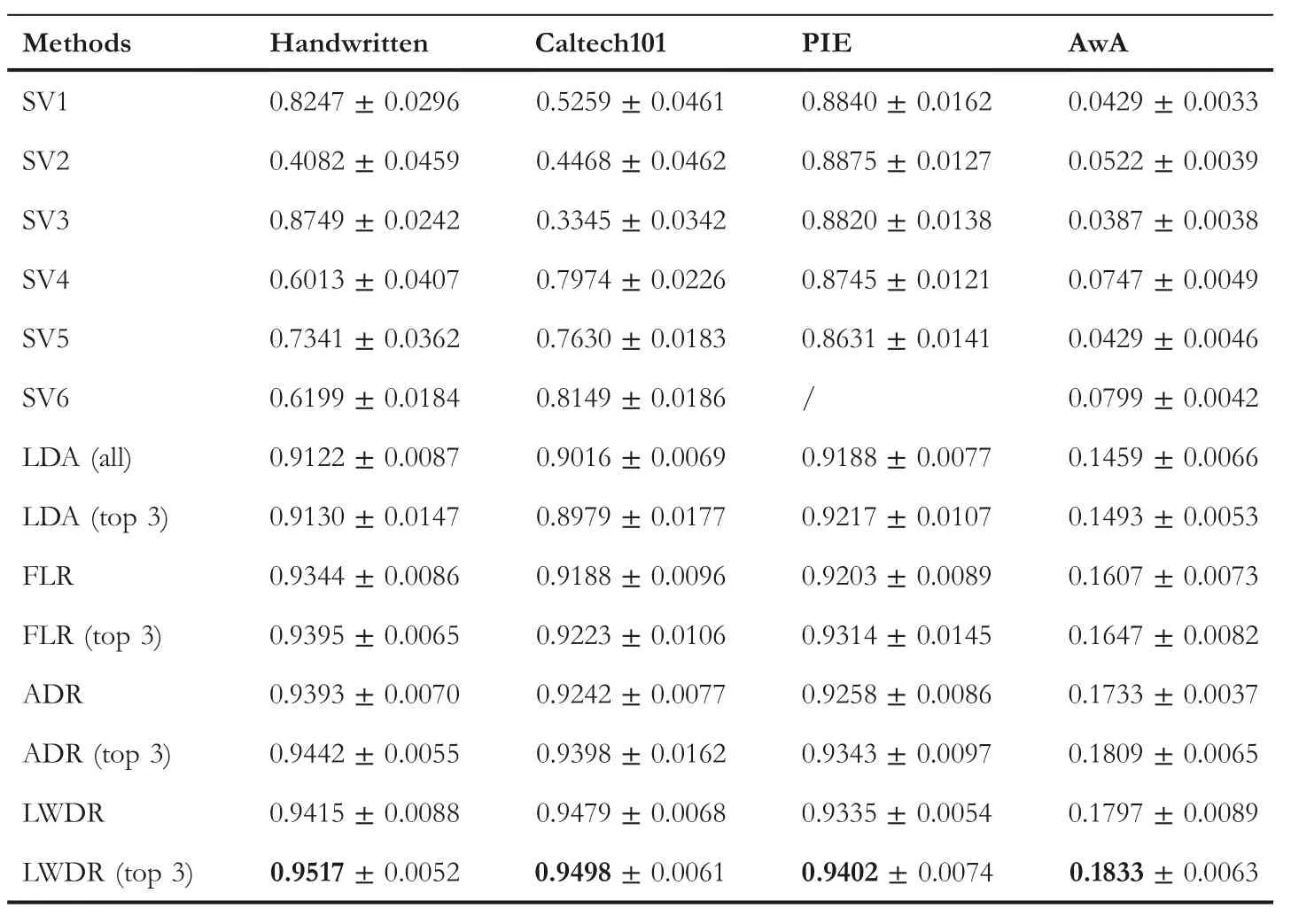
Table 2 lists the classification accuracies of single view and multi-view methods on Handwritten, Caltech101, PIE and AwA datasets.As can be clearly seen,our LDWR achieves the best performance on four datasets.SVi(i=1,2,…,6)denotes the single view method which performs LDA on the i-th view.The performance of SV varies significantly, which indicates that these views have different roles for classification. The simple concatenation of all views makes effects to improve the performance and LDA(all)is superior to all SV methods.LDA(top three)can generally produce better performance the LDA(all)except Caltech101 dataset.FLR learns a projection matrix for each view and adopts majority voting for classification,which obtain better performance than simple concatenation.ADR uses adaptive weight learning strategy and ϵ-dragging technique, and it performs better than FLR. However, our proposed LWDR still outperforms ADR on multi-view feature learning. For FLR, ADR and LWDR, the tops three views of four datasets are also tested.We can observe that by using the most informative top three views,these methods can generally better performance.

4.3.2 | Adaptive weights analysis

LWDR can automatically learn the weights of different views.The large weight means its corresponding view makes more contribution in feature learning. Table 3 lists the adaptive weights learned by LWDR on all views of Handwritten, Caltech101, PIE and AwA datasets. V1, V4, V3 and V6 have thelargest weight for the four datasets,respectively.From Table 2,these views also have good performance among all SV methods.These experimental results demonstrate that our LWDR can automatically pay more attention to those views which contain more discriminative information and make full use of them to learn discriminative features.

TA B L E 2 Classification accuracies of single view and multi-view feature learning methods on Handwritten, Caltech101, PIE and AwA datasets with nearest neighbour classifier. The best results are in bold

4.3.3 | Ablation study

In our proposed LWDR model (Equation 5), each view is assigned with an adaptively learned weight and a low-rank constraint is imposed on class-wise multi-view features to improve the intra-class compactness. To evaluate the effect of them separately, we conduct ablation experiments in this section.Two variations are derived from LWDR,that is,LWDR-s and LWDR-t.LWDR-s discards the weights learning in LWDR,that is, δk= 1. LWDR-t discards the low-rank constraint and directly uses the label matrix to guide the feature learning.The experimental results of LWDR and its two variations on four datasets are reported in Table 4. We can observe that LWDR outperforms LWDR-s and LWDR-t, which demonstrates thatthe adaptive weights and class-wise low-rank constraint are effective to boost the performance.

TA B L E 3 Adaptive weights learned by LWDR on four datasets

4.3.4 | Convergence analysis

In Section 3.2, we propose an iterative algorithm for solving our LWDR model. Here we illustrate its good convergence property by experiments. Figure 4 shows the convergence curves of proposed algorithm versus iterations on Handwritten, Caltech101, PIE and AwA datasets. It is obvious that the objective function value gradually decreases to a stable value with the increase of iterations.In particular,the proposed algorithm can generally converge within 20 iterations. The experimental results demonstrate that our algorithm is effective and efficient for solving LWDR model.

4.3.5 | Parameter analysis

There are three parameters, that is, α, β, γ, in LWDR which influence the performance of proposed method.To analyse the parameter sensitivity, we first define a candidate set {10-3,10-2,10-1,1,10,102,103}for α and γ,and{10-3,10-2,10-1,1,10,102}for parameter β.Then LWDR is conducted on four datasets with different combinations of the three parameters.Figure 3 shows the experimental results of LDWR versus α, γ and β on Handwritten, Caltech101, PIE and AwA datasets. It can be observed that,although all three parameters impact the performance of LWDR, LWDR can generally achieve satisfactory classification accuracy when α, γ and β locate in the range of [10-2, 10-1], [10-3, 10-2] and [10-2, 1] respectively.For example,when α,β,γ are selected from[10-2,10-1],[10-3,10-2] and [10-3, 10-1] respectively, the classification accuracy of LWDR is satisfactory.

TA B L E 4 Classification accuracies of LWDR and two variations

FIGURE 3 Classification accuracy (%) of LWDR versus α, β and γ on Handwritten, Caltech101, PIE and AwA datasets

FIGURE 4 The convergence curves of proposed algorithm for solving LWDR on Handwritten, Caltech101, PIE and AwA datasets

However,it is still difficult for optimal parameter selection on different datasets. In this article, we use the simple grid search for parameter selection[34]. We first fix β as a value in[10-3, 10-1] like 0.01, then find the optimal α and β by different combinations of the two parameters. After obtaining the optimal α and β,we can find the optimal β by searching in its candidate set.

5 | CONCLUSION

We propose a low-rank constrained weighted discriminative regression method for multi-view feature learning (LWDR).LWDR learns a common space across all views from a unified perspective. Each view is assigned with an adaptive weight, which enables the model to focus on the important views automatically. A low-rank constraint is imposed on the features of each class, which improves the intra-class similarity and enhances the model robustness. The strict sparse label matrix is relaxed by an l2,1-norm based regularization term. It is more flexible to deal with the errors in learning process. Experimental results on several popular datasets demonstrate the effectiveness of proposed method compared with some other single view and multi-view learning methods.

ACKNOWLEDGEMENT

The authors would like to thank the editor and anonymous reviewers for their constructive and valuable comments and suggestions. This work was partially supported by National Key Research and Development Program of China(No. 2018YFB1402600, 2016YFD0702100), and National Nature Science Foundation of China (Nos. 71671086,71732003).