Constrained tolerance rough set in incomplete information systems

Renxia Wan| Duoqian Miao | Witold Pedrycz

1School of Mathematics and Information Science, North Minzu University,Yinchuan,Ningxia,China

2Hongyang Institute for Big Data in Health,Fuzhou, Fujian,China

3Department of Computer Science and Technology,Tongji University, Shanghai,China

4Department of Electrical and Computer Engineering,University of Alberta,Edmonton,Canada

Abstract The tolerance rough set is developed as one of the outstanding extensions of the Pawlak's rough set model under incomplete information, and the limited tolerance relation is developed to overcome the problem that objects leniently satisfy the tolerance relation.However,the classification based on the limited tolerance relationship cannot reflect the matching degree of uncertain information of objects. In this article, we explore the influence of null values in an incomplete system, and propose the constrained tolerance relation based on the matching degree of uncertain information of objects.The proposed rough set based on the constrained tolerance relation can provide a more detailed structure of an object class through threshold.Proofs and example analyses further show the rationality and superiority of the proposed model.

1 | INTRODUCTION

The classical rough set model[1,2],proposed by Pawlak in the early 1980s, is a powerful mathematical tool for data analysis.The rough set theory has been widely used in pattern recognition, machine learning, decision analysis, knowledge acquisition and data mining [3–10]. In the past few decades, due to the diversity of data and different requirements of analysis purposes,the extended rough set models have been developed,such as the variable precision rough set model[11],probability rough set model [12, 13], game-theoretic rough set [14, 15],fuzzy rough set model [16, 17], local neighborhood rough set[18] and so on.

However,there are two factors that limit the application of the rough set:firstly,the classical rough set model and most of its extensions are basically based on the equivalence relation which possesses reflexive,symmetric and transitive properties.The equivalence relation is relatively strict condition in many practical application, and classes clustering on this relation cannot well reflect the natural characteristic of the overlapping data set; secondly, the classical rough set requires the information of processed object should be complete,however,quite a few data objects in practical applications are incomplete or inconsistent, and even with null values [19].

Many scholars have conducted research works for substitution of the equivalence relation [20–23], some scholars also describe the concept of target through multiple indiscernibility relations and propose a multi-granularity rough set model[24–27]. In these works, Skowron and Stepniuk [28] replaced the equivalence relation with the tolerance relation and proposed the tolerance approximation spaces, Skowron and Stepniuk [28] replaced the equivalence relation with the tolerance relation and proposed the tolerance approximation spaces, and Kryszkiewicz [19] defined a similarity relation in incomplete information systems. Kryszkiewicz's similarity relation is an extension of Skowron's tolerance relation,therefore, both of them are referred to as tolerance relation collectively by later researchers.The tolerance relation discards the transitivity requirement of indiscernibility relation in the classical rough set and relaxes the symmetry requirement for incomplete information. Hence, the tolerance classes can well reflect the overlapping relation between groups of objects.Dai[29] defined the fuzzy tolerance relation in the complete numerical data set and established the fuzzy tolerance rough set;Kang and Miao [30] proposed an extended version of the variable precision rough set model based on the granularity of the tolerance relation. Xu et al. [27] extended the singlegranulation tolerance rough set model to two types of multigranulation tolerance rough set models from a granular computing view. Stefanowski and Tsoukias [20] introduced non-symmetric similarity relation which can refine the results obtained using the tolerance relation approach, and they also proposed valued tolerance relation in order to provide more informative results; however, Wang [21] found that the symmetric similarity relation may lose some important information and valued tolerance relation requires accurate probability distribution of all attributes in advance, Wang then proposed the limited tolerance relation.Deris et al.[31]used conditional entropy to handle flexibility and precisely data classification in limited tolerance relation. There are also some scholars who studied alternatives to missing values. Nakata and Sakai [32]used possible equivalence classes to approximate the set of attributes having missing values.Yang[33] computed attribute reduction with the related family.Hu and Yao[34]introduced a logic formula to describe incomplete information tables.

In this article,we propose the constrained tolerance rough set model in the term of matching degree of incomplete information. The rest of the article is organized into four parts.In Section 2,we review some related concepts.In Section 3,we present constrained tolerance relation as an improved version of limited tolerance relation and analyse the properties of the proposed rough set model. In Section 4, the method of measuring the uncertainty of the proposed roughed set model is given and the superiority of the model is further verified.Finally, Section 5 concludes the paper.

2 | RELATED CONCEPTS

In this section, we review some basic concepts such as information system,Pawlak's rough set,tolerance rough set,limited tolerance rough set.

Definition 2.1 [19, 31]. An information system (IS)is a 4-tuple S=(U,TA,V,f), where U=｛x1,x2,…,x｜U｜｝ is a non-empty finite set of objects,TA=｛a1,a2,…,a｜TA｜｝ is a non-empty finite set of attributes, V =∪a∈TAVa,Vais the value set of attribute, f :U×TA →V is a total function such that f(x,a)∈V, for every (x,a)∈U ×TA, called information function.If U contains at least one object with an unknown or missing value (so-called null value),then S is called incomplete information system(IIS). The unknown value is denoted as “*” in the incomplete information system. In this article, we also use the quadruple S=(U,TA,V,f) to denote an incomplete information system.TA=C ∪D If,where C is the set of condition attributes, Dis the set of decision attributes,then S is called Decision Information System.

Each subset of attributes A ⊆TA determines a binary indiscernibility relation IND(A) as follows:

IND(A)=｛(x,y)∈U ×U｜∀a ∈A,a(x)=a(y)｝.

The relation IND(A)is an equivalence relation since it is reflexive, symmetric and transitive.

Definition 2.5 [21]. Let S=(U,TA,V,f) be an IIS,A ⊆TA, and PA(x)=｛a｜a ∈A ∧a(x)≠*｝. A binary relation L(limited tolerance relation)defined on U is given as L is reflexive and symmetric, but not transitive. The limited tolerance class ILA(x) of an object x with reference to an attribute subset A is defined as ILA(x)=｛y｜y ∈U ∧LA(x,y)｝.

3 | ROUGH SET BASED ON CONSTRAINED TOLERANCE

From Definition 2.5,we can easily derive an equivalent form of the limited tolerance relation as following:

It means that the objects with all attributes being null will be judged to be limited tolerating and then should be grouped into the same limited tolerance class. However, in practical application, the risk of classifying those objects whose attributes filled with a quit mount of null values will greatly arise. In fact, we prefer to control the scale of null-valued attributes within a certain range. Meanwhile,the more the properties of the two objects with the same value, the greater the probability of being divided into the same class and the higher the classification accuracy.However, the limited tolerance may group those objects with only one attribute of the same value into the same class.

We can illustrate the above phenomena considering the following example with an IIS described as Table 1.

Example 3.1 Suppose Table 1 is a IIS, where x1,x2,…,x16, are objects, a1,a2,a3,a4are four condition attributes,d is a decision attribute. The domains of these four condition attributes are all {0, 1, 2, 3}. The domain of the decision attribute d is {H, J}

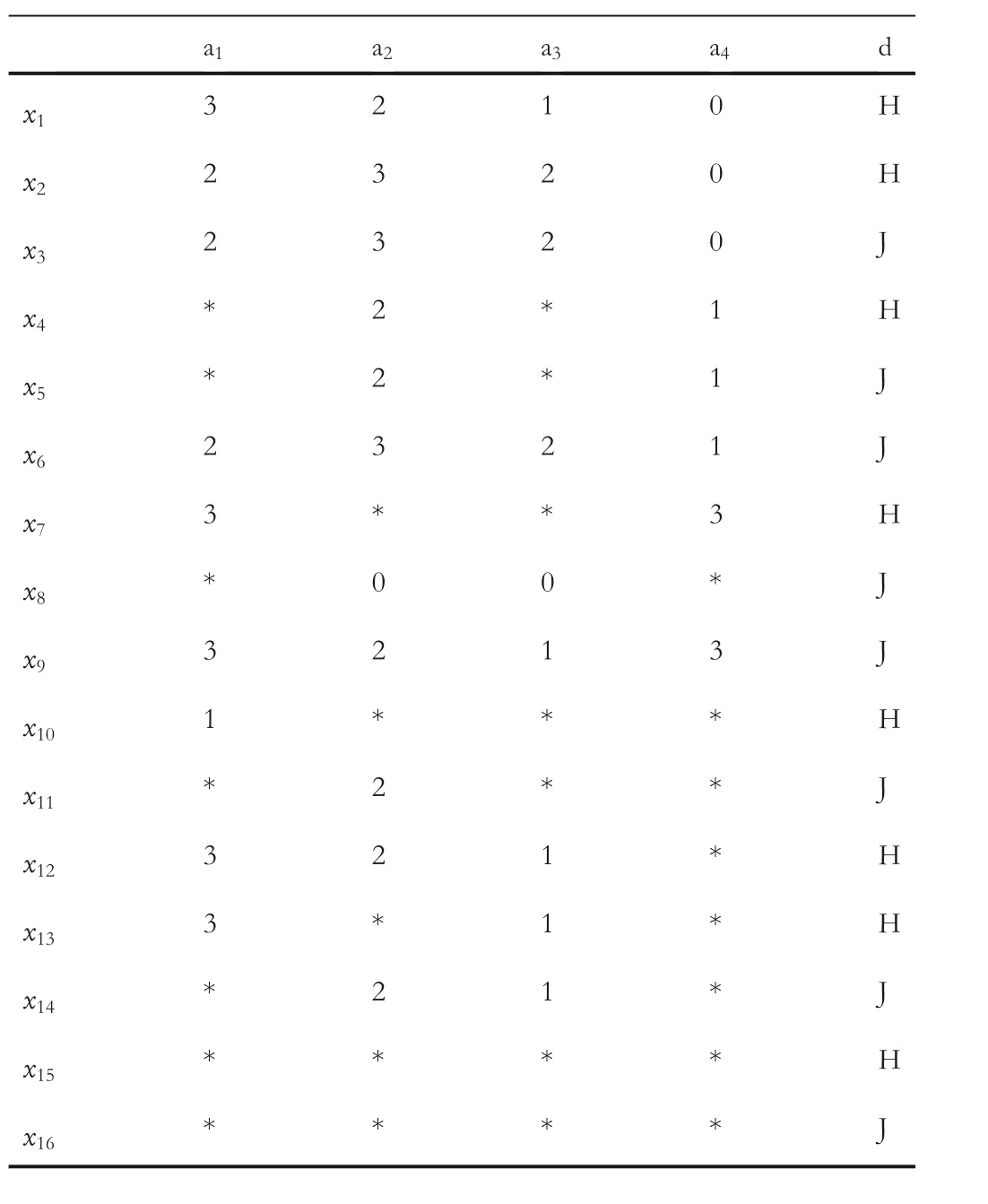
TABLE 1 An incomplete information table

Let A=｛a1,a2,a3,a4｝,we can easily obtain the following results by analysing Table 1 with the limited tolerance relation.

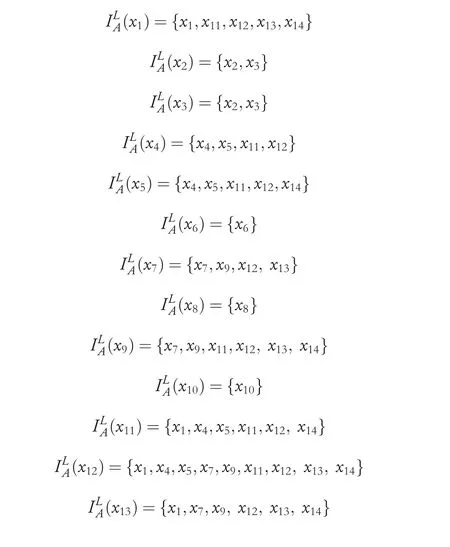
For data analysis, the elements in the lower approximation of the data set are expected to be representative of the final classes. In Table 1, all conditional attributes of x15and x16are null; intuitively, they should be classified as outliers (special classes) in most practical applications, but from the above results, the particularity of x15and x16is not shown in the lower approximation of ‘H’ or ‘J’, because the classification based on the limited tolerance relation is not able to distinguish the influence degree of the null value attribute.

In order to improve the accuracy of object classification based on tolerance relations and reflect the influence degree of null value,in this article,we propose the constrained tolerance relation.Definition 3.1 Let S=(U,TA,V,f) be an IIS,and QA(x)=｛a｜a ∈A ∧a(x)=*｝,A ⊆C,x,y ∈U,the incomplete matching degree ρ of x and y is defined as

Herein, a(x)=a(y) involves the situation that(a(x)=*)∧(a(y)=*).

Obviously,the constrained tolerance relation is symmetric,reflexive, but not transferable.

Since ∀a∈A(a(x)=a(y)≠*) means that ρA(x,y)=0 is always true. Thus, similar to the limited tolerance relation, we can easily derive an equivalent form of the constrained tolerance relation.

Proposition 3.1 reveals the relationship between the constrained tolerance relation and limited tolerance relation when τ ∈[0,1),then if τ=1,what structure the constrained tolerance relation may have?

From Definition 3.2,we know the inequality ρ(x,y)≤1 is always true when τ=1. If ρ(x,y)=α, where α is a constant for a given pair(x,y),and α ＜1,from Proposition 3.1,we have(x,y)∈Tcτ(A)⇒(x,y)∈L(A); If ρ(x,y)=1, it means that,for any α ∈A, at least one of a(x)and a(y) is null. At this point,x and y become outliers of each other's class in terms of the constrained tolerance class or the limited tolerance class.

That is,when τ=1,the constrained tolerance relation will retrograde into the tolerance relation and the constrained tolerance class will retrograde into the tolerance class.

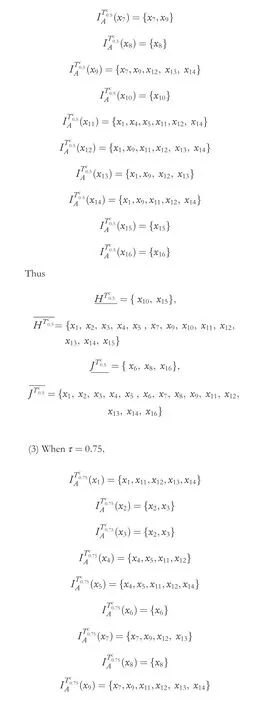
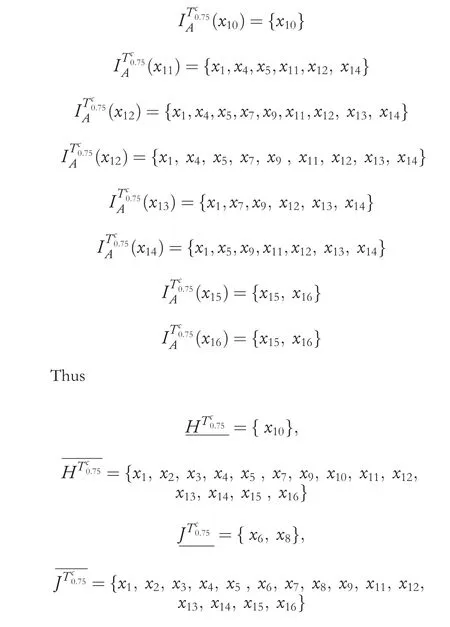
From the above results,we can find that the scale of lower approximation of ‘H’ (or ‘J’) decreases when the threshold τ increases. It intuitively indicates that the classification boundary area or the classification uncertainty of objects will increase with the increment of τ. It echoes exactly to Proposition 3.3.With a further discuss,due to the objects in Table 1 only have four condition attributes,τ=0.75 means that two objects can be of the same constrained tolerance class if there are no more than three attribute values between them that are alternately or simultaneously null. That is, the two objects have no less than one attribute value being simultaneously non-null and completely satisfy the judgement criteria of the limited tolerance class.Thus,under this condition,the produced classes of objects and the upper and lower approximations of ‘H’ or ‘J’are the same as what Example 3.1 shows.

4 | MEASUREMENTS IN CONSTRAINED TOLERANCE ROUGH SET

There may be uncertainty of an object set(category)because of the existence of a borderline region.The greater the borderline region of set,the lower may be the accuracy of the set.In order to measure such uncertainty, similarly to literatures [1, 27, 35],we develop the accuracy measure of the constrained tolerance rough set.

Definition 4.1 Let S=(U,TA,V,f) be an IIS,A ⊆TA,∀X ⊆U (X ≠∅). The accuracy measures of X in constrained tolerance rough set is defined as

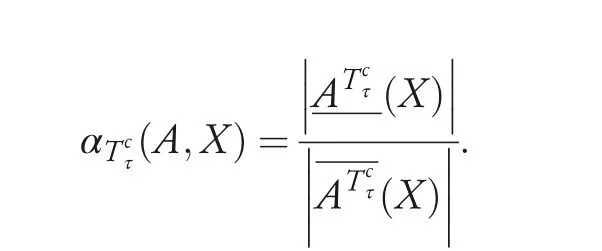
Similarly,we can give the accuracy measures of X in limited tolerance rough set as follows:

TABLE 2 Accuracy measures

The above theorem delivers a further understanding of the relationship between limited tolerance sets and constrained tolerance sets.

Example 4.1 From the results of Examples 3.1 and 3.2, we can directly calculate accuracy measures of the limited relation rough set and the constrained rough set as shown in Table 2.

5 | CONCLUSION

The tolerance rough set is developed as one of extensions of Pawlak's rough set model under incomplete information.Wang[20] proposed the limited tolerance relation to overcome the problem that objects leniently satisfy tolerance relation.However, the classification based on the limited tolerance relationship cannot reflect the matching degree of uncertain information of objects, while, in some practical applications,the matching degree of uncertain information of objects is of great influence on the final classification.

In this article,we propose the constrained tolerance rough set model in the term of matching degree of incomplete information.The proposed rough set not only inherits the merit of the limited tolerance rough set, but also provides a more detailed structure of object class through threshold.

Further research may include the multi-granulation version of the constrained tolerance rough set and extensions of other rough set under constrained tolerance.

ACKNOWLEDGMENTS

The authors wish to thank Prof. Yiyi Yao for his constructive suggestions on this study. This work is supported by the National Natural Science Foundation of China (61,662,001,61,762,002), Young and Middle-aged Talents Training Program of National Ethnic Affair Commission (2016GQR06),Ningxia First-class Construction Discipline Program(NXYLXK2017B09), Open Foundation of Ningxia Key Laboratory of Intelligent Information and Big Data Processing(2019KLBD006).

ORCID

Renxia Wan https://orcid.org/0000-0003-1966-0597