钢板剪力墙-RC 框架结构基于能量平衡的大震塑性设计
2022-01-12金双双白久林李梦依
金双双,谢 雨,白久林,李梦依
(1. 省部共建山区桥梁及隧道工程国家重点实验室,重庆交通大学,重庆 400074;2. 重庆交通大学土木工程学院,重庆 400074;3. 重庆大学土木工程学院,重庆 400045)
钢板剪力墙结构是一种具有承载力高、耗能能力强、延性好等优点的抗侧力体系。通过在普通钢板剪力墙两侧增加约束盖板来抑制薄钢板的屈曲,即形成屈曲约束钢板剪力墙;约束盖板不参与结构受力,仅对钢板剪力墙的屈曲起约束作用。已有的研究[1− 4]表明,屈曲约束钢板剪力墙的抗侧力滞回曲线饱满,承载能力和耗能能力强,具有良好的抗震性能。两边连接屈曲约束钢板剪力墙(SPSW)是一种仅与框架梁连接的抗侧力体系构件,SPSW 能够减小对框架柱的作用力,避免框架柱过早发生破坏,而且布置灵活,便于门窗洞口的开设,受到设计人员和科研人员的关注并对其性能与应用进行了广泛的研究[5−8]。将SPSW 设置在钢筋混凝土框架结构(RCF)中形成双重抗侧力结构体系(如图1 所示),RCF 将会产生附加的刚度和强度,提高结构的抗震性能,降低结构的震后损伤。

图1 两边连接屈曲约束钢板剪力墙-钢筋混凝土框架结构Fig. 1 SPSW-RCF structure
目前,钢板剪力墙结构的抗震设计主要有基于强度和基于性能的设计方法。基于强度的设计方法已广泛应用于规范[9− 11]中,但该方法无法预测和评估结构的性能,因此基于性能的抗震设计方法应运而生。金双双等[12]通过考虑钢板剪力墙极限塑性状态以及框架对其承载力的贡献,提出了考虑边缘框架贡献的钢板剪力墙结构设计方法。Ghosh 等[13− 14]以最大层间位移角为性能指标,基于目标延性和预设的屈服机制,提出了钢板剪力墙基于性能的塑性设计方法。孙国华等[15]通过考虑结构损伤与地面运动加速度的关系,引入延性比,并结合标准化的滞回耗能谱,提出了钢板剪力墙结构基于能量的性态抗震设计方法。郝际平等[16]通过修正楼层剪力来考虑结构的P-∆效应,选用目标位移和预期的破坏模式作为结构的两个关键性指标,提出了钢板剪力墙结构基于性能的塑性设计方法。Driver 等[17]提出了以延性和极限延性为性能指标的SPSW 基于性能的抗震设计方法,并对钢板剪力墙的屈服机理进行了研究。于金光等[18]基于“强框架,弱墙板”的设计理念以及钢板剪力墙的破坏顺序,根据叠加原理确定部分组合柱内力计算原则,提出了部分组合框架-钢板剪力墙框架柱的设计方法。上述提出的抗震设计方法多应用于四边连接钢板剪力墙与钢结构的组合体系中,而将SPSW 设置在RCF 中形成SPSW-RCF 双重抗侧力结构体系的性能设计方法还鲜见报道。在大震作用下,SPSW-RCF 结构将产生较大的侧向变形,RCF 以剪切变形为主,SPSW以弯曲变形为主;RCF 的承载力逐渐退化,而SPSW 的承载力有强化现象;RCF 体系与SPSW 体系具有明显不同的变形模式和承载机制。
为此,在前期钢筋混凝土框架结构和BRBRCF 结构基于能量平衡的塑性设计方法[19− 20]的基础上,提出SPSW-RCF 结构基于能量平衡的大震塑性设计方法。通过综合考虑SPSW 和RCF 的耗能特性、预期的屈服机制和目标位移,构建SPSW-RCF 结构大震一体化破坏模式可控设计;采用塑性设计方法设计两个5 层和10 层结构,并对两个结构进行非线性动力分析,验证一体化塑性设计方法对实现预期抗震性能的有效性。
1 SPSW-RCF 双重抗侧力结构体系
在设计的过程中考虑结构的竖向荷载和水平地震作用,将SPSW-RCF 双重抗侧力结构体系离散成SPSW 体系和RCF 体系,如图2 所示。RCF体系承担整个结构的竖向荷载和部分水平地震作用FF,SPSW 则承担另一部分的水平地震作用FB。考虑结构的最优破坏模式和预期的“强柱,弱梁,更弱的墙板”的屈服机制,全部钢板剪力墙、所有梁端以及首层柱柱底将发生屈服。

图2 SPSW-RCF 结构在竖向荷载和大震作用下的整体破坏模式Fig. 2 Schematic of SPSW-RCF structure yielding in a global mechanism under vertical load and great earthquake action
在水平地震作用下可以分别用双线性能力曲线来近似表示SPSW 体系和RCF 体系的能力曲线,SPSW-RCF 结构的能力曲线可用两个结构体系的能力曲线之和表示,则能力曲线变为三线性曲线,如图3 所示。SPSW-RCF 结构体系的基底剪力、SPSW 体系的基底剪力以及RCF 体系的基底剪力分别为:


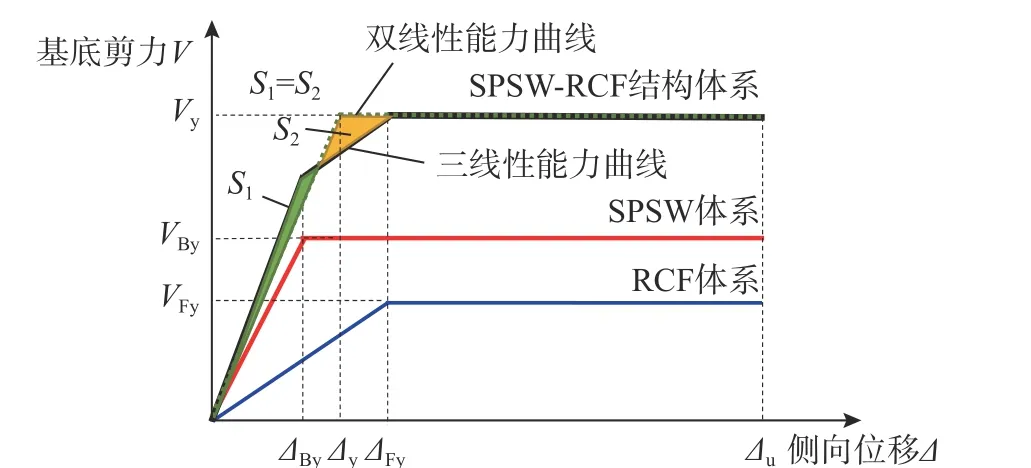
图3 SPSW-RCF 结构的能力曲线及其双线性近似Fig. 3 Capacity curves of SPSW-RCF structural system and its bilinear approximation
假设RCF 体系和SPSW 体系的屈服位移分别为∆Fy和∆By,根据能量平衡原理(S1=S2)将结构的三线性能力曲线等效为双线性能力曲线,如图3所示,可以计算SPSW-RCF 结构的屈服位移:

式中, ρ为SPSW 体系屈服位移与RCF 体系屈服位移的比值,即ρ=∆By/∆Fy。
2 基于能量的SPSW-RCF 结构塑性设计方法
2.1 设计基底剪力和设计侧向力
从Housner[21]提出能量平衡的抗震设计理念后,诸多学者对此设计理念进行了研究[22−24],现在基于能量平衡的设计方法已成为抗震设计的重要手段。大震塑性设计方法根据能量平衡的原则和结构的屈服机制来对结构进行设计,该方法将多自由度SPSW-RCF 结构体系(MDOF)的能力曲线等效成理想弹塑性单自由度体系(EPP-SDOF),如图4 所示。通过修正的能量平衡方程使未重合部分的面积近似相等,即EPP-SDOF 体系消耗的能量近似等效为其对应的多个弹性单自由度体系(E-SDOF)消耗的能量之和。
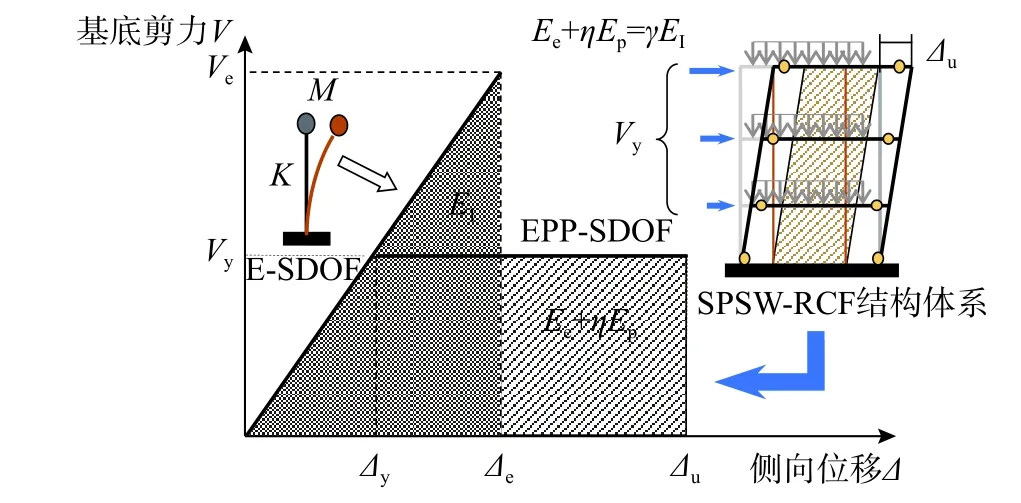
图4 SPSW-RCF 结构的能量平衡示意图Fig. 4 Illustration of energy balance concept for SPSW-RCF structure
文献[19]通过考虑结构滞回性能对结构耗能能力的影响和高阶模态能量的贡献,提出了修正能量平衡方程:


式中:∆Fi为重力二阶P-∆效应的附加侧向力;Wi第i层的楼层重量; θu为结构的目标位移角。
2.2 结构塑性内力设计
根据2.1 节FDi以及SPSW 体系所承担的剪力比p分别计算SPSW 体系的楼层侧向力FBi和RCF 体系的楼层侧向力FFi:
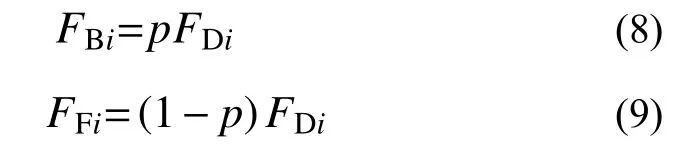
FFi和FBi分别独立作用在RCF 体系与SPSW体系中形成预期的屈服机制,如图5 所示。
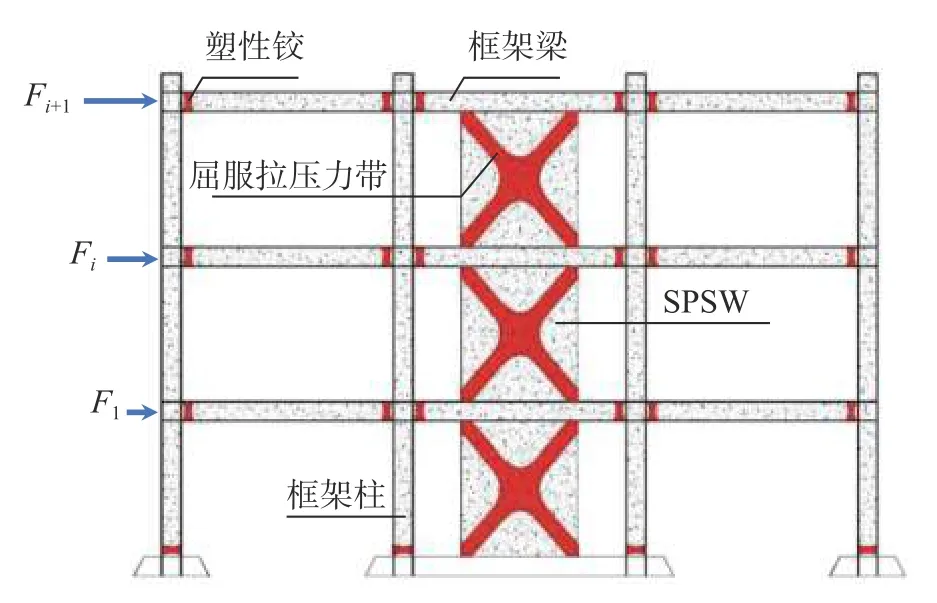
图5 SPSW-RCF 结构屈服机制Fig. 5 Yielding mechanism of SPSW-RCF structure
对于RCF 体系的内力计算可参考文献[19]。
对于SPSW 体系,楼层分布侧向力FBi完全由SPSW 剪切屈服来抵抗。先通过FBi计算出楼层剪力VBi,钢板墙的厚度可参照钢板剪力墙技术规程[26]进行计算:
当0.5≤b/h≤1.0时,

根据实际选用的钢板墙厚度tb计算钢板墙的屈服承载力Vywi以及楼层剪力VSi。
要精确地模拟钢板墙的受力行为,必须确定合理的交叉带倾角和交叉支撑偏心距,等效支撑模型如图6 所示(钢板墙设置在跨中)。文献[27]提出当钢板墙高宽比较小时(h/b<1.5),支撑点的位置可取在距钢板墙边缘e=0.1h处;当钢板墙高宽比较大时(h/b≥1.5),支撑点的位置可取在距钢板墙边缘e=b/6处;文献[28]表明在等效支撑点处,支撑力可等效为垂直力0.5Vywitanα 和水平力0.5Vywi,受力情况如图7 所示。
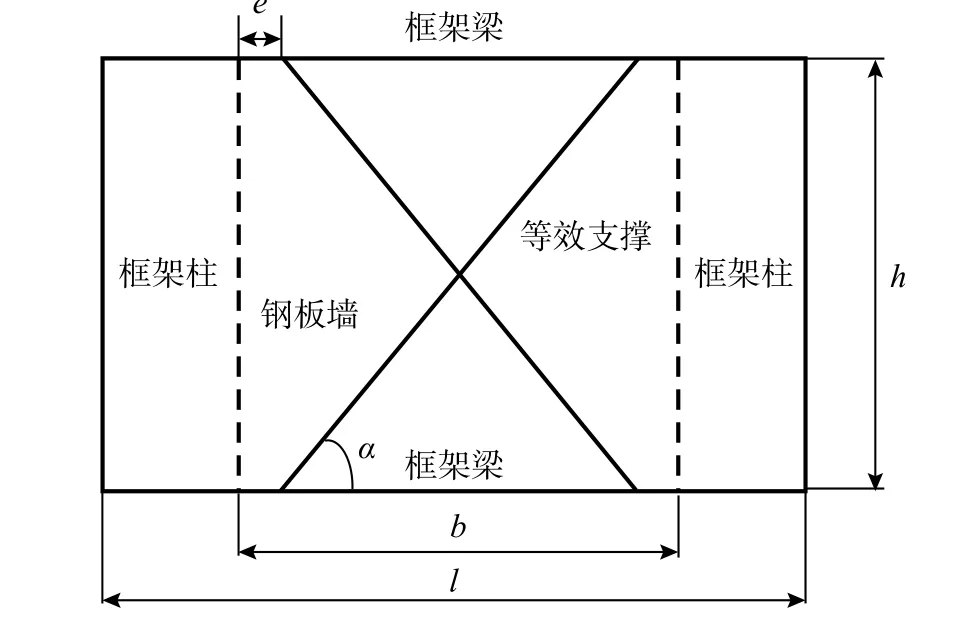
图6 SPSW 等效支撑模型Fig. 6 Equivalent cross brace model for SPSW
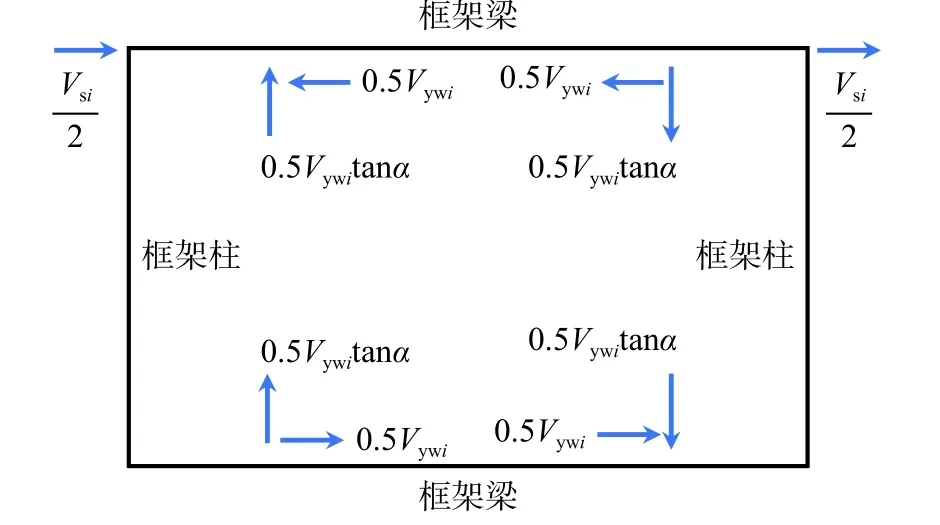
图7 SPSW 边缘构件受力图Fig. 7 Bracing force on frame for SPSW

2.3 设计流程
1)根据抗震设计规范[11]要求以及工程经验,选取SPSW-RCF 结构的目标屈服位移角 θu、整体破坏模式以及SPSW 承担的基底剪力比p。
2)设计框架结构梁、柱截面尺寸以及钢板墙的高度h和宽度b,计算结构塑性位移角和设计位移延性。根据规范[26]SPSW 的屈服位移角可表示为:

式中: εy为钢筋屈服应变;Lb为梁净跨;hb为梁截面高度。计算出 θBy和 θFy后,计算SPSW 体系与RCF 体系的屈服位移比ρ=θBy/θFy,再按照式(4)计算出SPSW-RCF 结构的层间位移角 θy。SPSWRCF 结构的塑性位移角 θp和设计转角延性μs为:θp=θu−θy,μs=θu/θy。
3)对弹性结构和刚度折减结构(结构在目标侧移下混凝土会出现开裂和破碎,结构刚度会降低,按照规范设计要求,应对弹性结构进行刚度折减,折减系数取值为0.85)进行模态分析,得到弹性结构的基本周期和刚度折减结构的前3 阶模态参数。
4)计算结构的能量修正系数 γ以及滞回耗能修正系数 η。
5) 按照式(6)计算结构的设计基底剪力Vy,并根据式(7)计算结构的楼层侧向力FDi。
6)根据SPSW 体系所承担的剪力比p计算出SPSW 的楼层剪力VBi,按照式(10)或式(11)计算出钢板剪力墙的厚度t。
7)迭代上述第3)步~第6)步,直到迭代前后结构通过模态分析所得的周期基本相近,确定SPSW 设计参数tb。需要注意的是,第一次迭代没有添加SPSW 体系,先按照纯RCF 体系获得设计基底剪力。
近年,城市暴雨洪涝灾害凸显出城市防灾教育宣传不足,城市居民普遍缺乏防洪减灾意识。特别是城市外来务工、出差、旅游、临时来访等人员,往往成为宣传教育死角,其防灾避险意识和知识更加缺乏,易造成不必要的人员伤亡。2013年第19号强台风“天兔”袭击广东,在防御台风过程中,有14名群众因顶风外出,被倾倒树木、电线、高空坠物等砸中导致死亡,暴露出公众面对灾害时避险意识和自救知识的严重匮乏,应急处理能力亟待提高,防灾减灾知识宣传教育工作需要进一步加强。
8)根据文献[19]计算RCF 的构件内力。
9)按照式(12)~式(15)计算钢板剪力墙传递给梁、柱的内力。
10)将第8)步和第9)步计算出的内力叠加,根据内力需求进行框架梁、柱构件的截面设计,并满足规范最小配筋要求[11,29]。
3 设计实例
为了验证SPSW-RCF 结构塑性设计方法的有效性,本文以5 层结构和10 层结构为例,通过详细的塑性设计和非线性动力分析来验证。
3.1 结构的参数设定
5 层和10 层的结构具有相同的平面布置,结构平、立面布置图如图8 所示,层高为3.3 m。考虑到SPSW 沿纵跨布置,仅选取纵跨中间榀框架作为分析对象。SPSW 布置在中间跨,SPSW 采用Q235B 钢材,钢板墙两侧的约束盖板采用100 mm厚的混凝土板,钢筋采用HRB400,混凝土强度为C30;结构屋面活荷载和恒荷载分别为2.0 N/mm2和6.0 N/mm2。对于5 层的结构,梁、柱尺寸分别为250 mm×500 mm 和500 mm×500 mm。对于10 层的结构,1 层~5 层梁、柱尺寸分别为300 mm×550 mm 和550 mm×550 mm,其他梁、柱尺寸同5 层结构梁、柱尺寸;SPSW 的宽度取值为2 m。结构的抗震设防烈度为8 度,场地的特征周期为0.35 s。由于计算大震下的地震作用,场地特征周期增加0.05 s。两个结构的设计参数见表1。
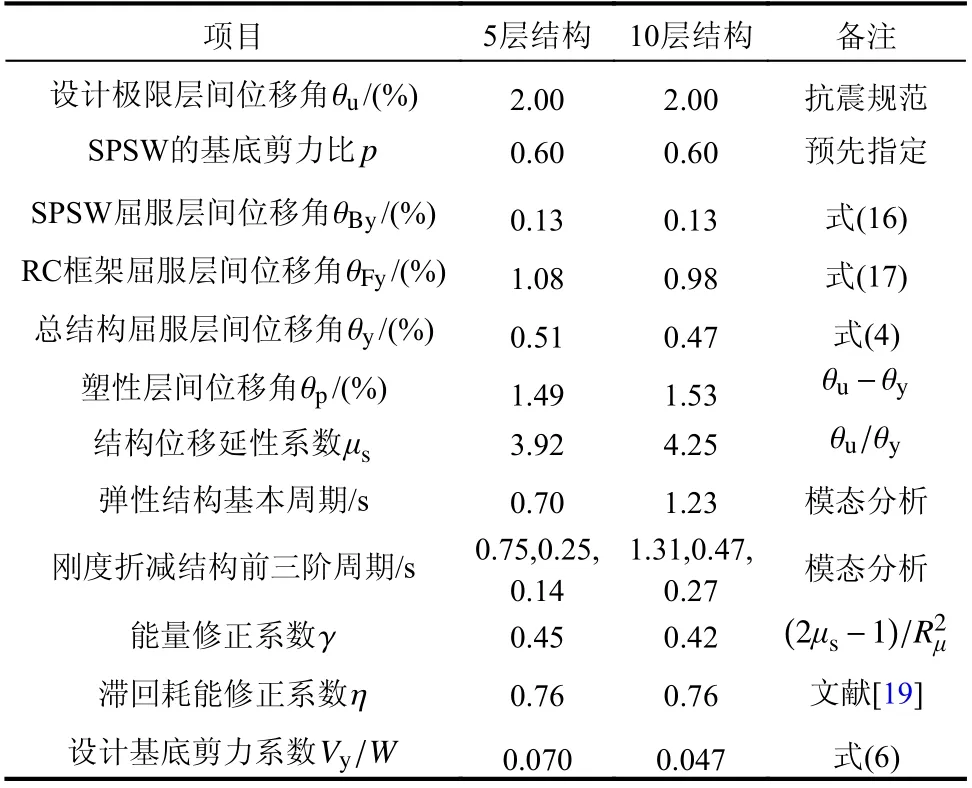
表1 结构设计参数Table 1 Parameters for structural design
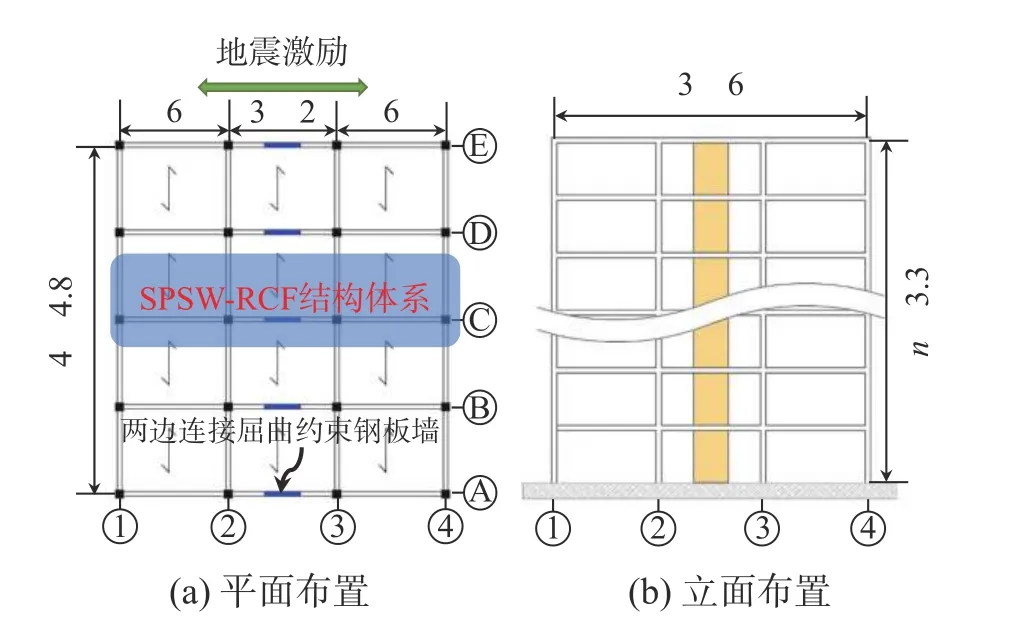
图8 结构布置图 /mFig. 8 Structural model schematic diagram
3.2 结构的塑性设计
根据2.3 节设计流程进行钢板剪力墙参数设计,RCF 梁、柱内力计算。由于梁轴力小,梁截面配筋主要由弯矩控制,SPSW 对柱的弯矩影响小,对柱轴力影响大,因此给出梁弯矩、柱轴力的内力图,分别为图9、图10(5 层结构和10 层结构计算过程相同,因篇幅所限只给出5 层结构的内力图)。根据构件内力和规范[11,29]需求,梁、柱的配筋率以及SPSW 截面设计如表2 所示。
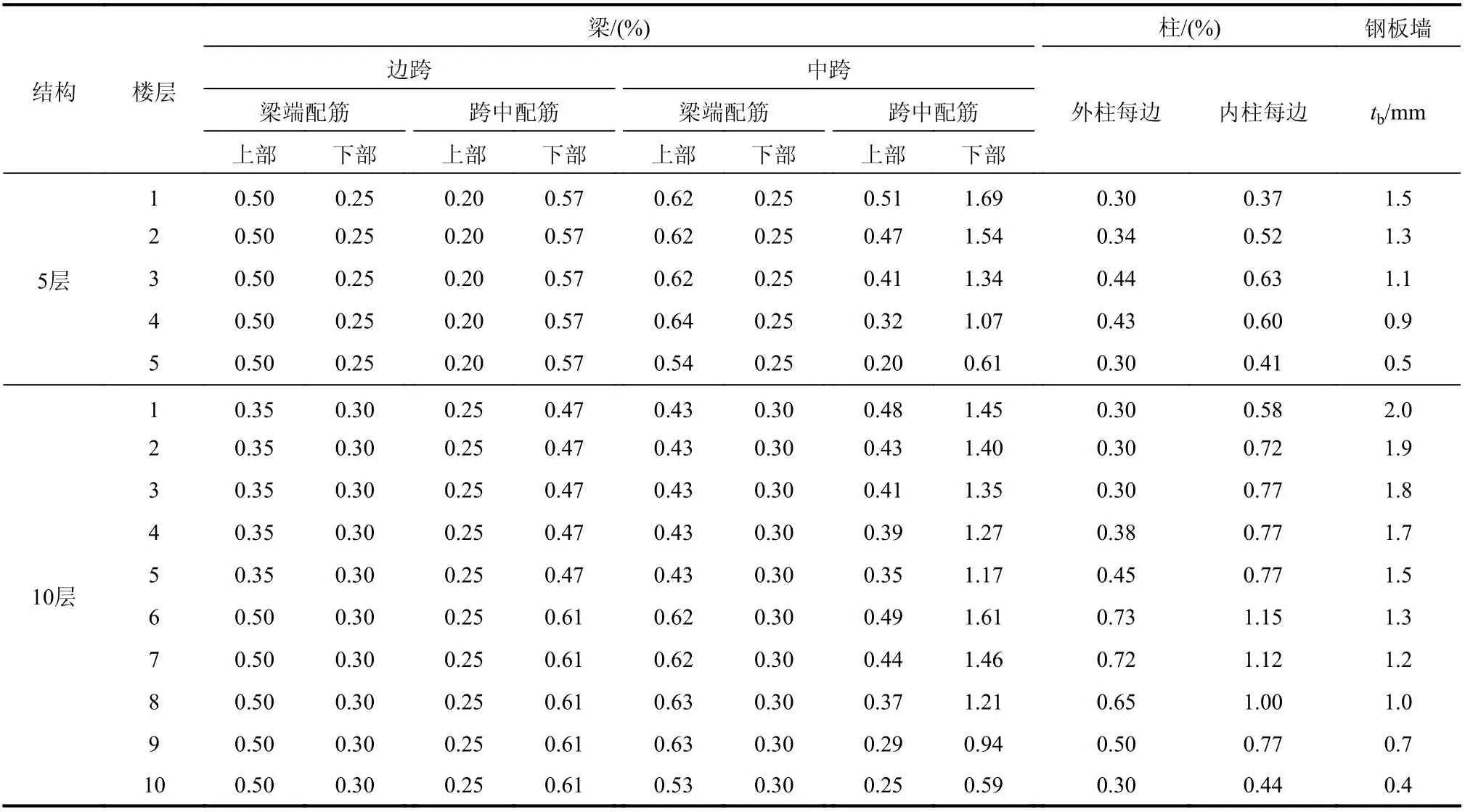
表2 RCF 构件纵向配筋率和钢板墙参数确定Table 2 Sectional longitudinal reinforcement ratio for RCF and determined SPSW configurations
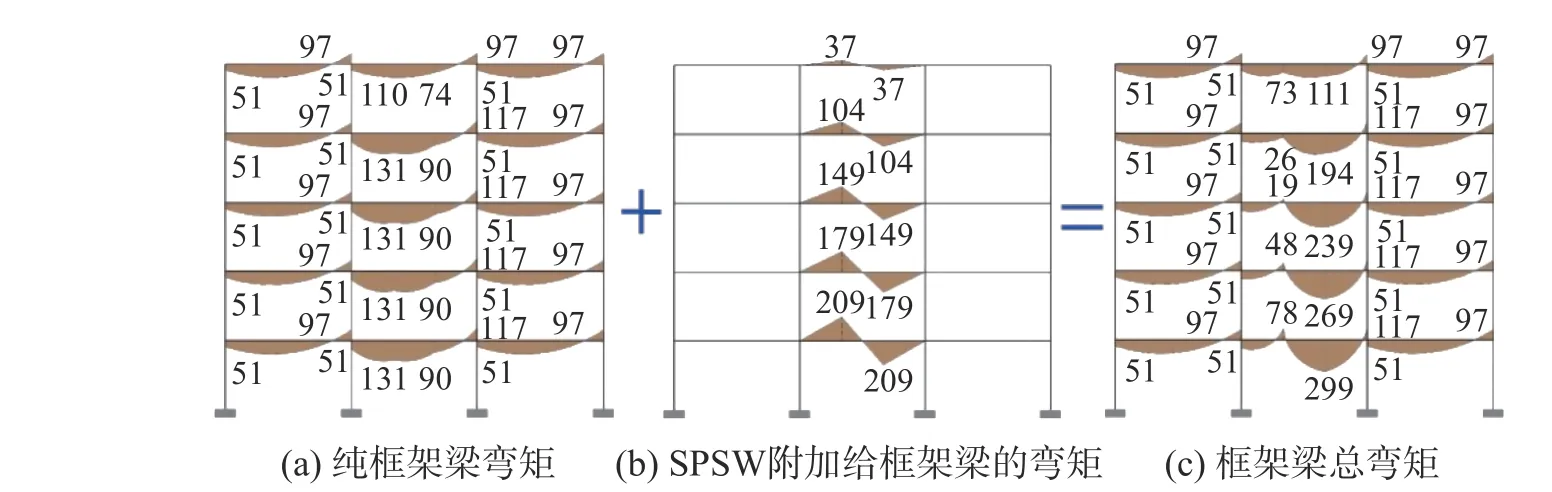
图9 5 层结构梁弯矩图 /(kN·m)Fig. 9 Moment of beam for 5-story building

图10 5 层结构柱轴力图 /kNFig. 10 Axial force of column for 5-story building
4 分析结果
4.1 结构模拟方法
用OpenSees 软件建立非线性动力分析模型并对其进行分析。考虑结构中框架梁端和首层柱底会出现塑性铰,梁和首层柱采用Beam With Hinges单元进行模拟,并且取梁截面有效高度作为塑性铰的长度[19];其他层柱采用Nonlinear Beam Column单元进行模拟;混凝土采用Concrete01 本构模型,钢筋采用Steel02 本构模型;采用纤维模型来模拟截面轴力和弯矩的耦合效应。考虑混凝土开裂会降低结构的刚度,则梁的有效刚度取弹性刚度的0.5 倍,柱的有效刚度取弹性刚度的0.7 倍。分析时,考虑结构重力二阶P−∆效应并取5%的Rayleigh 阻尼。
分析时若采用实体模型模拟SPSW 性能,过程复杂、计算量大,则将SPSW 等效为交叉杆模型。本文根据文献[30]采用Truss 单元来模拟SPSW等效交叉杆,通过杆件在拉压荷载作用下的滞回规律来模拟SPSW 的滞回性能。两根交叉杆具有相同的本构关系,在模拟的过程中交叉杆采用Hysteretic 材料模型,其应力-应变关系如图11所示。图中: σy为杆的屈服强度, εy为杆的屈服应变, σu为杆的极限强度, εu为杆的极限应变,Es为钢板墙的弹性模量,As为杆的截面面积,Py、Px分别为钢板墙不同高厚比和跨高比的捏缩因子,Ky为钢板墙的初始刚度, α为杆的倾角。
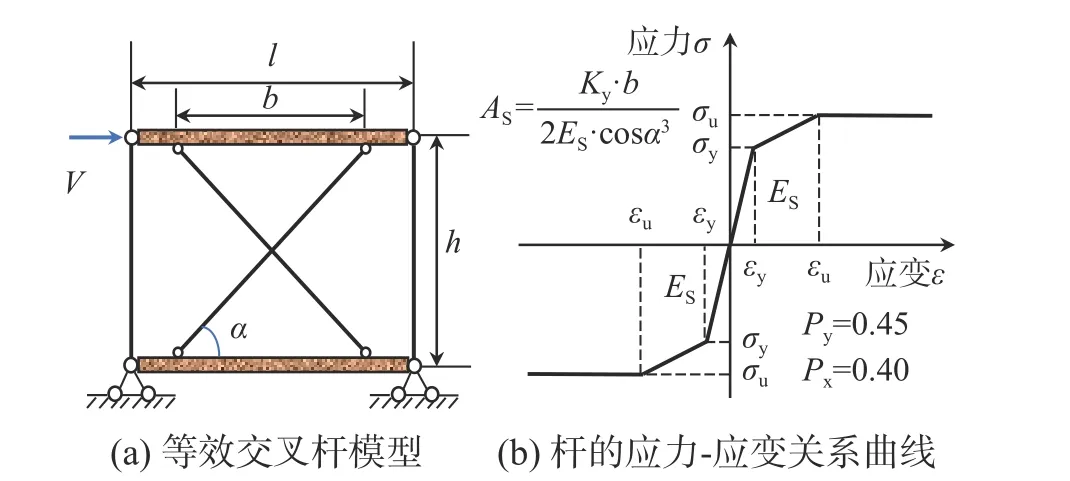
图11 等效交叉杆模型及杆应力-应变关系曲线Fig. 11 Equivalent cross truss model and stress-strain curve of truss
为验证上述模型能较好地模拟SPSW 体系,采用文献[30]实验中的F2CSW1 作为模拟对象,OpenSees 模拟值与实验值对比如图12 所示,可以看出模拟的滞回曲线与试验的滞回曲线拟合较好,证明了等效交叉杆模型的适用性。需要注意的是,在分析过程中,SPSW 仅承担水平地震荷载,因此在RCF 施加完竖向荷载后,再添加SPSW 体系。
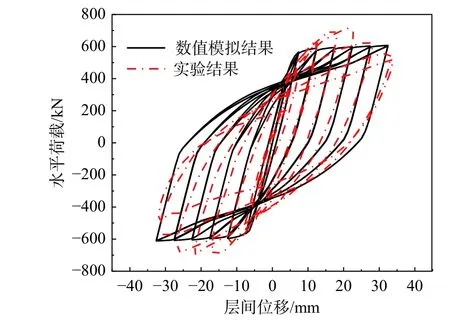
图12 数值模拟值和实验对比Fig. 12 Comparison between model and experimental date
4.2 地震动选取
选用FEMA P695 中22 条远场地震动对结构进行非线性动力分析,地震动的信息参考文献[19],每条地震动,选取两个分量中反应谱更加接近规范反应谱的地震动。根据我国抗震规范[11],将所有地震动调幅到PGA 为4.0 m/s2,调幅后的地震动反应谱如图13 所示。
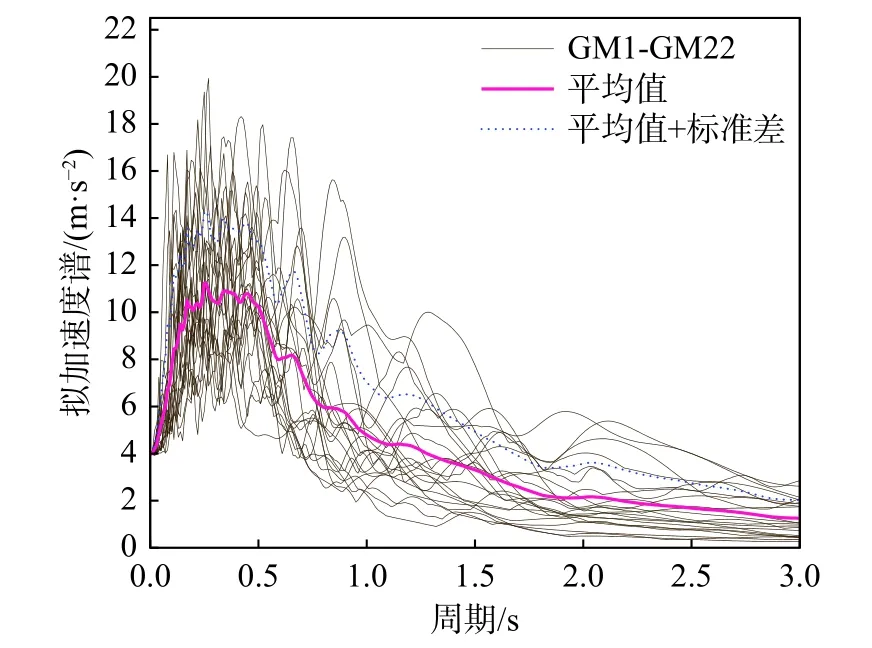
图13 调幅后地震动的反应谱(5%阻尼比)Fig. 13 Response spectra of scaled ground motions (damping ratio 5%)
4.3 非线性动力分析
选用地震动来对结构进行非线性动力分析。分析内容包括层间位移角响应、楼层剪力比、损伤机制及结构残余变形。根据分析结果来评估结构在大震作用下的抗震性能以及验证塑性设计方法的有效性。
4.3.1 层间位移角
图14 为两个结构在大震作用下的最大层间位移角响应,同时给出了22 条地震动下最大层间位移角的平均值和平均值±标准差。从图中可以看出,5 层结构仅有2 条地震动的最大层间位移角大于2%,最大值为2.12%,10 层结构只有1 条地震动的最大层间位移角大于2%,最大值为2.26%;两个结构平均最大层间位移角的最大值出现在中间层,最大值分别为1.06%和0.90%,平均值 ±标准差均小于2%,满足抗震设计规范规定的限值和塑性设计时结构的目标位移角。两个结构的最大层间位移角响应表明:由于在设计过程中考虑了结构的非弹性性能和结构的整体破坏模式,结构在大震作用下的层间变形得到控制,证明了本文设计方法的有效性。
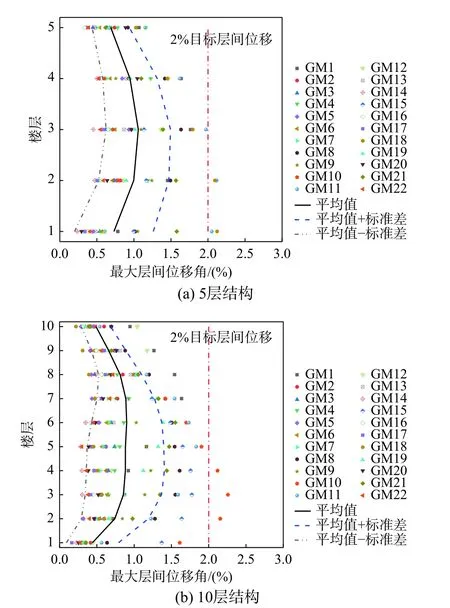
图14 强震下结构的最大层间位移角分布Fig. 14 Interstory drift ratio distribution of structures under severe earthquakes
4.3.2 楼层剪力比
图15 为两个结构在大震作用下SPSW 的楼层剪力比分布,同时给出了22 条地震动下楼层剪力比的平均值和平均值±标准差。从图中可以看出,5 层结构和10 层结构在每条地震动下SPSW 的楼层剪力比和在22 条地震动下楼层剪力比的平均值以及平均值±标准差都在0.4 左右,且最大值出现在中间层。两个结构SPSW 的楼层剪力比分布表明:SPSW 充分发挥其耗能能力,SPSW 楼层剪力比的离散性小,SPSW-RCF 结构能离散成2 个独立的结构体系;验证了本文设计方法能使钢板墙充分耗能并能离散双重抗侧力体系,为双重抗侧力体系的设计提供了设计依据。
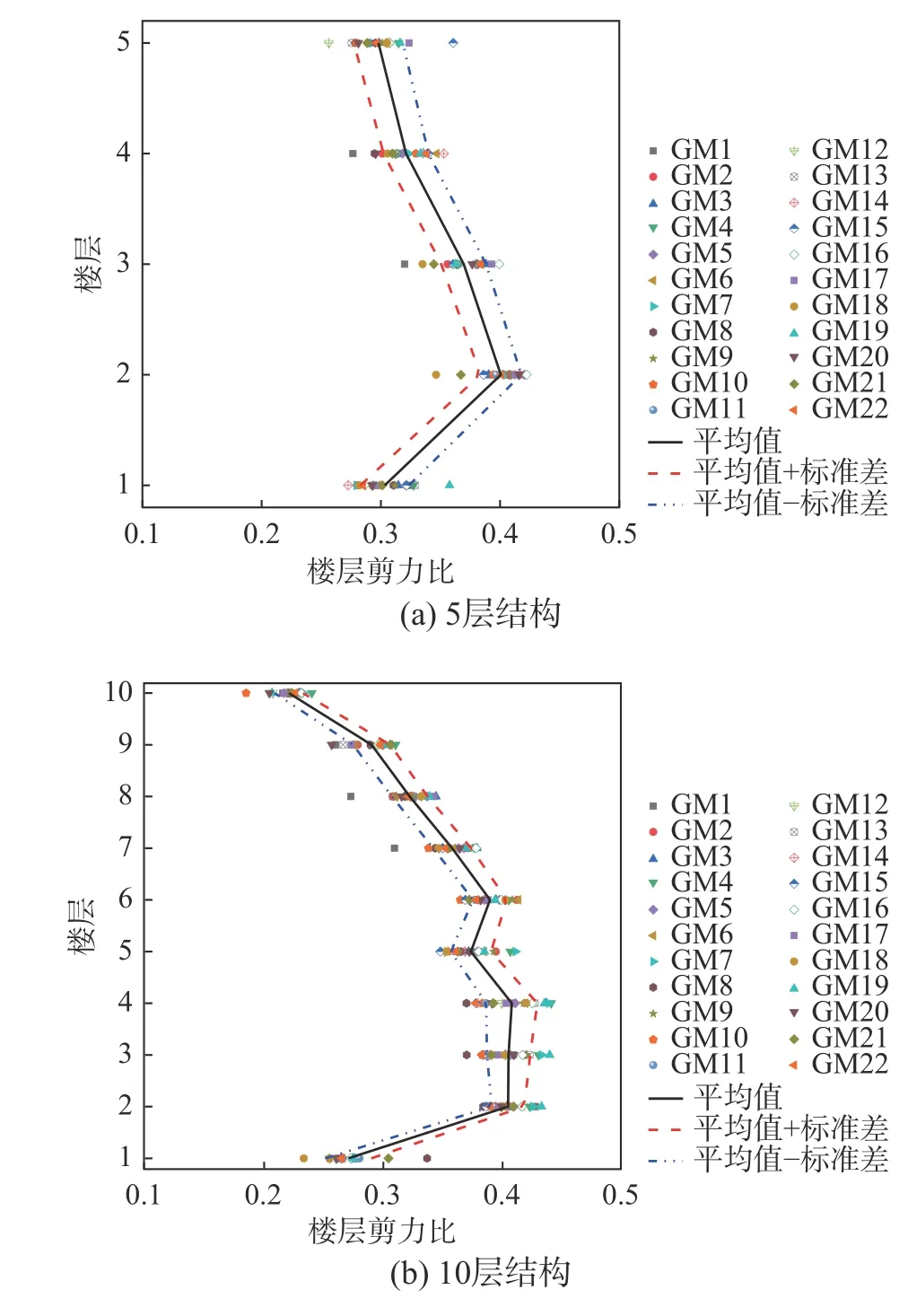
图15 两边连接屈曲约束钢板剪力墙的楼层剪力比Fig. 15 Median normalized story shear resisted by SPSW system
4.3.3 损伤机制
图16 为两个结构的在22 条地震动下的屈服机制和RCF 梁、柱构件平均塑性转角;在不同地震动下结构会形成不同的屈服机制,若22 条地震动中有一条地震动使构件发生屈服,便认为构件屈服。从图中可以看出,在22 条地震动作用下,首层柱柱底和所有梁端均出现塑性铰,其他层柱保持弹性状态,所有的钢板墙屈服;中间层梁端的塑性铰转动较大,但结构首层柱柱底和梁端塑性转角平均值均小于0.013 rad。两个结构的损伤机制表明:本文设计方法不仅能实现SPSW-RCF结构的最优破坏模式和“强柱,弱梁,更弱的墙板”的屈服机制,还使SPSW-RCF 结构具有极强的鲁棒性。
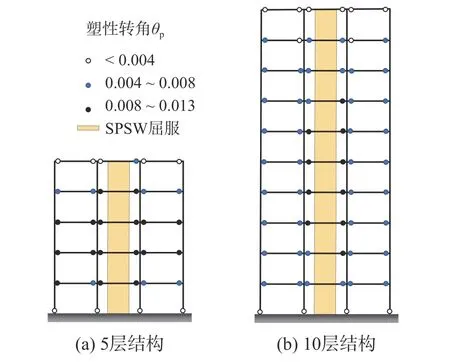
图16 22 条地震动下结构塑性铰分布和平均塑性转角Fig. 16 Plastic hinges distribution and mean plastic rotation demands under 22 ground motions
4.3.4 结构残余变形
图17 为两个结构在大震作用下的结构残余变形,同时给出了22 条地震动下残余层间位移角的平均值和平均值+标准差。从图中可以看出,在每条地震动下,结构的残余层间位移角均小于2%,残余层间位移角的平均值和平均值+标准差都小于0.5%;结构的残余层间位移角与最大层间位移角密切相关,5 层和10 层结构的残余层间位移角的最大值也出现在中间层。结构的残余变形表明:通过本文设计方法设计的SPSW-RCF 结构具有较好的可修复性能。
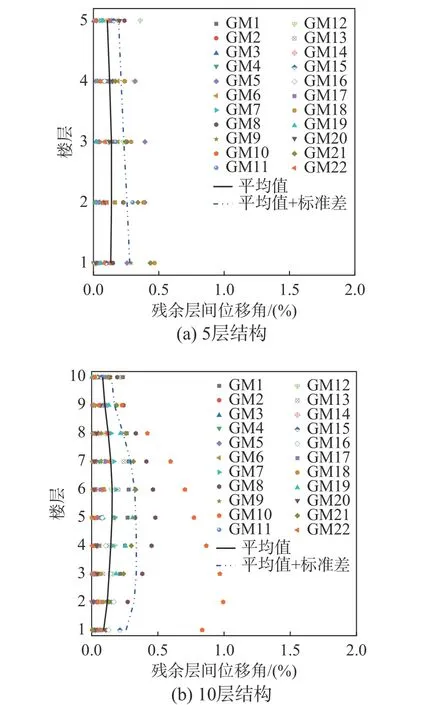
图17 结构残余层间位移角Fig. 17 Residual drift ratio demands of structures
5 结论
本文提出了SPSW-RCF 结构基于能量平衡的大震塑性设计方法,通过对两个结构算例的设计与分析,得出以下结论:
(1)通过预设SPSW 承担的剪力比p将总结构体系离散为SPSW 体系和RCF 体系,便于计算结构的屈服位移和各独立体系的层间剪力,使得SPSW 和RCF 的设计更加明确。
(2)本文设计方法以预定目标位移和整体破坏模式为主要的性能指标,在设计的过程中可考虑SPSW 体系屈服后的性能和RCF 体系梁、柱塑性内力的分配机制。
(3)本文设计方法能直接体现结构“强柱,弱梁,更弱的墙板”的抗震设计思想,结构最大层间位移角和残余位移角均满足规范要求,SPSW 能充分耗能,表明了基于能量平衡的大震塑性设计方法的有效性。
