考虑损伤的软弱夹层剪切流变模型及程序实现

2022-01-12魏二剑

水利水运工程学报 2021年6期

祝鑫，胡斌，李京，崔凯，魏二剑，刘杨

(1. 武汉科技大学资源与环境工程学院，湖北武汉 430081； 2. 冶金矿产资源高效利用与造块湖北省重点实验室，湖北武汉 430081)

岩土体的流变性质复杂，其本构模型研究是流变力学理论研究的一大难点、热点问题，同时也是数值试验研究的模型基础。国内外许多学者经过对岩体微细观破裂机制的不断研究，发现岩体在荷载作用下的应变与破坏主要表现为断裂形式与损伤形式，且越来越多的学者更倾向于应用损伤的观点来构建相应的流变模型。赵延林等[1]将伯格斯模型和摩尔库仑塑性损伤元件串联建立了新的蠕变损伤模型；杨圣奇等[2]结合损伤力学与有效应力观点，推导了岩石在两阶段中的损伤演化方程，建立了能较好描述岩石流变三阶段的损伤流变模型；Ma等[3]应用Lemaitre应变等效理论引入损伤变量，提出了基于广义Hoek-Brown准则的非线性损伤模型；胡波等[4]考虑蠕变起始的应力阈值，将一种阶跃函数表示的开关与广义K体并联，并引入损伤变量对CVISC模型进行了改进；徐卫亚等[5]在流变不同阶段引入不同函数和损伤变量，建立了绿片岩的改进的广义Bingham模型；伍国军等[6]建立了适用于工程岩体的黏弹塑性损伤本构模型；陈铁林等[7]将结构性黏土看作由结构体和结构面双重介质组成，在堆砌体模型的基础上，采用过应力理论，建立了结构性黏土的流变模型；张强勇等[8]将岩体流变力学参数看作是非定常的，构建了变参数的蠕变损伤本构模型；Yang等[9]根据不同围压下煤的短期和蠕变试验结果，提出了新的损伤演化方程，建立了一个新的非线性蠕变损伤模型；陈卫忠等[10]建立了盐岩蠕变损伤的本构方程和损伤演化方程；张亮亮等[11]推导出损伤变量的演化方程，用于黏塑性模型中的黏性参数，得到了一种新的岩石损伤蠕变模型。

随着计算机软硬件的不断发展，各种数值分析软件应运而生，适用于岩土体领域的软件也与日俱增，使得岩土体的数值研究不断涌现出新成果。但是，实际工程岩体具有非均质性，其各向异性明显，力学性质复杂，与数值模拟软件自带的本构模型差别较大。因此，进行自定义本构模型的开发成为了一种研究趋势，目前已取得一定的研究成果。胡浩[12]提出一种基于分数阶微积分的本构模型，基于FLAC3D软件进行开发，并用隧道注浆加固的算例验证了其有效性；褚卫江等[13]给出了西原流变损伤模型在FLAC3D中实施的程序流程；徐平等[14]研制了广义Kelvin模型的FLAC3D接口程序，并对基坑开挖进行了实例分析；杨文东等[15]基于FLAC3D开发了改进Burgers蠕变损伤模型，并验证了黏弹性、塑性和损伤的力学性质；谢秀栋等[16]开发了软土弹黏塑性流变模型，通过模拟侧向卸荷流变试验，并与修正剑桥模型作比较，验证了二次开发的可行性；何利军等[17]使用C++语言实现了含SMP强度准则的黏弹塑性模型的开发，为其他强度准则的开发提供了参考；蒋邦友等[18]同时考虑岩石材料的塑性及损伤共同作用，完成了基于Mogi-Coulomb准则的岩石弹塑性损伤本构模型的程序实现。

在自然界中，岩体多数处于挤压、剪切的状态，其变形和破坏的主要形式是沿着滑面的剪切破坏，且主要表现为剪切流变损伤特征，对岩体破坏主要考虑的因素是剪切应力[19]。本文通过对软弱夹层不同剪切应力水平下的试验数据进行分析，建立一个考虑流变损伤的软弱夹层剪切流变模型，并基于FLAC3D软件，使用C++语言进行自定义模型的代码编写，最后验证开发模型的正确性。

1 剪切流变损伤本构模型建立

软弱夹层的剪切流变一般经历减速、稳定及加速流变阶段。其中，加速流变阶段的变形速率会越来越快，变形迅速增大，且无法收敛，最终发生破坏。现有的软弱夹层流变模型的建立主要有两种方法，其一是在经典流变模型的基础上增加新的非线性元件进行组合；其二是将损伤力学等新理论、观点引入本构模型中，以此建立非线性流变模型。

本文基于Kachanov流变损伤理论[20]，引入流变损伤变量D来描述流变过程中软弱夹层参数的变化。损伤变量D是流变过程中岩体材料不断劣化，强度不断减小的量化指标，其具体表现形式为：

式中：t为时间。当t=tD（临界破坏时间）时，D=1，则可得：

由式（2）、（3）可得损伤演化方程为：

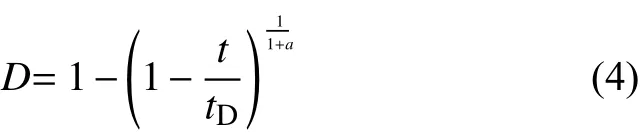
图1 为随时间增加，不同a取值情况下流变损伤变量D的变化，可以看到，a取值不同，流变损伤变量D的变化快慢也不相同，但是在时间t趋近破坏时间tD时，其变化率趋近于无穷大，此时D趋近于1，表明已完全损伤，处于破坏状态。

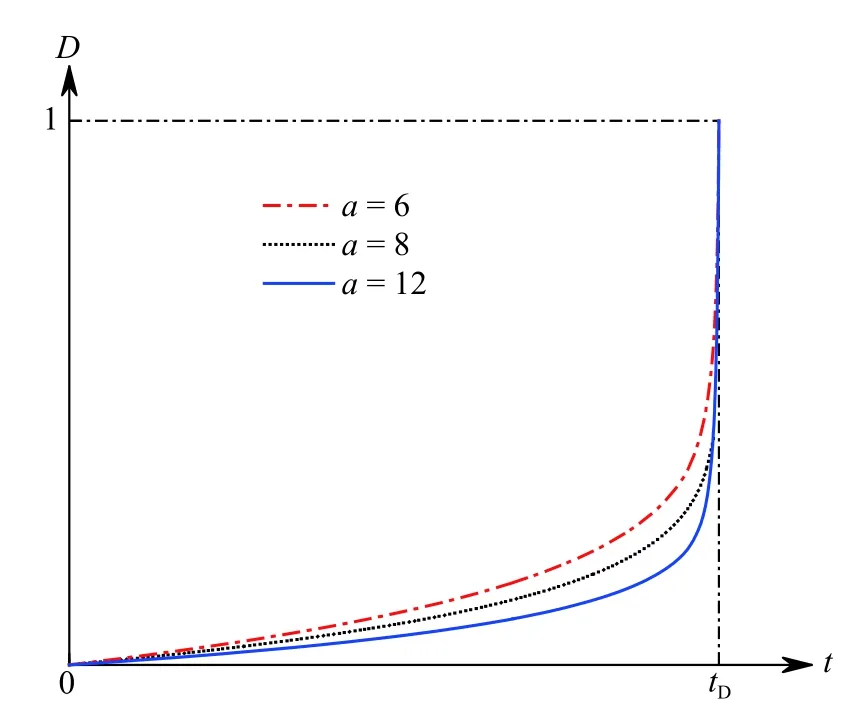
图1 a不同取值下损伤变量D的趋势曲线Fig. 1 Trend curve of damage variable D under different values of a

基于流变损伤变量D，提出一个能够描述软弱夹层加速流变阶段的黏弹塑性流变模型，见图2所示。

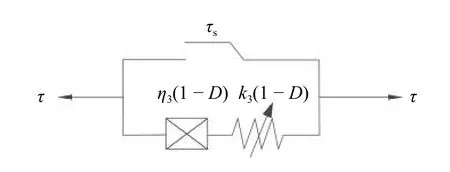
图2 黏弹塑性流变模型Fig. 2 Viscoelastic plastic rheological model

软弱夹层的剪切流变是黏、弹、塑性等多种变形共同作用的过程，要使用基本线性元件及其他非线性元件的串并联组合形式进行描述，对于减速、稳定两个阶段可以采用常规的伯格斯模型进行描述，对于加速流变阶段需要采用能够描述黏弹塑性特征的模型进行模拟。因此，本文将黏弹塑性流变模型与伯格斯模型串联起来，可以同时描述软弱夹层的减速、稳定及加速流变3个阶段的流变过程（图3）。

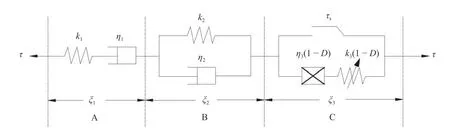
图3 非线性流变损伤模型Fig. 3 Nonlinear rheological damage model

由模型的串联关系可知，建立的软弱夹层非线性流变损伤组合模型满足以下条件：

式中：τ1、τ2、τ3分别为模型A、B及C组件剪应力（MPa）；ξ 为总应变量，ξ1、ξ2、ξ3分别为模型A、B及C组件产生的应变量。

根据剪切屈服应力τs与 τ 之间的关系，所建立的软弱夹层非线性流变损伤模型的流变方程需分为以下两种情况：

（1）τ ＜τs时，模型中C组件不工作，流变方程为：

式中：k1、η1、k2、η2分别为A和B组件中的弹性系数（GPa）及黏性系数（GPa·h）。

（2）τ ≥τs时，C组件开始工作，流变方程为：

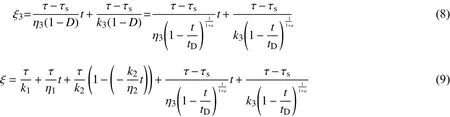
式中：k3、η3分别为C组件的弹性系数（GPa）和黏性系数（GPa·h）。

式（9）可以同时描述软弱夹层的减速流变、稳定流变和加速流变3个阶段的流变变形过程。

2 流变损伤模型的三维差分形式

为了将本文所提出的损伤本构模型导入FLAC3D，需要将模型的流变方程改写为FLAC3D所能识别差分格式，主要包括偏应力增量和流变时间的关系及应变增量与流变时间的关系。

由模型串联规则可以得到，总偏应变增量为A组件马克斯韦尔体、B组件开尔文体、C组件黏弹塑性体3个偏应变增量的和。即：

式中：ij表示各个分量方向分别为马克斯韦尔体、开尔文体、黏弹塑性体的偏应变增量。

对于A组件的马克斯韦尔体，由弹性元件与黏性元件串联而成，其偏应变增量为：

对于B组件开尔文体，由弹性元件与黏性元件并联而成，其偏应力与模型总偏应力Sij相等，且与其偏应变平均值偏应变增量的关系为：

式中：k2、 η2分别为开尔文体的弹性系数（GPa）和黏性系数（GPa·h）。

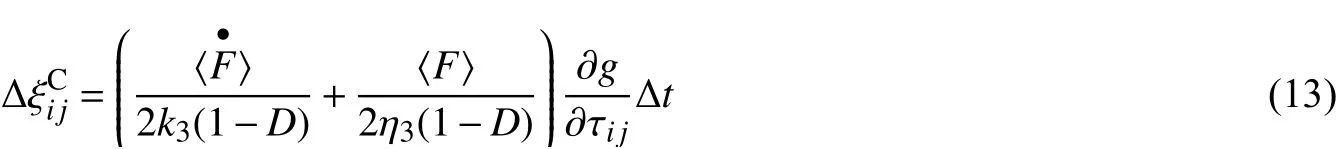
又因为式中：

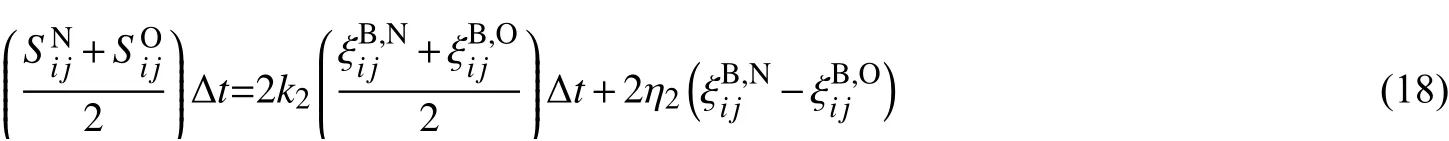
求解可得：

将式（11）、（13）、（16）、（18）代入式（10）并化简可得：

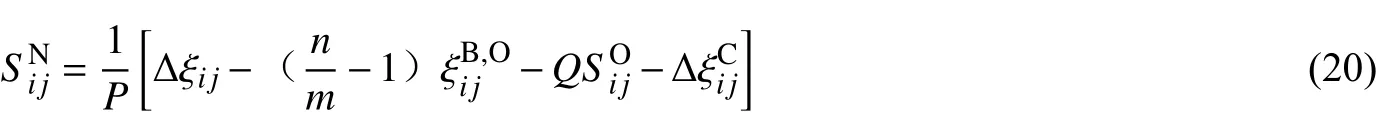
其中：

模型中的球应力张量不发生塑性应变，满足下列关系式：

最终的总应力张量可以分解为球应力张量σm和偏应力张量Sij，即：

3 剪切流变损伤模型二次开发

流变损伤本构模型的开发在Microsoft Visual Studio 2015软件环境下完成。由于在FLAC3D中，损伤变量D形式较为复杂，无法写成流变时间的增量差分格式，因此，损伤变量的定义采用FLAC3D软件自带的FISH语言进行编写，具体为使用FISH语言将本文推导的损伤演化方程定义为一个函数，随着流变时间的变化，损伤变量也发生变化，进而相应的模型参数也发生变化，以此实现参数的损伤演化过程。

本文开发的软弱夹层剪切流变损伤模型主要包括：（1）模型开发插件、开发平台软件及解决方案的生成；（2）模型的名称、注册ID、版本号、自定义变量k1、n1、k2、n2、k3、n3及部分中间变量等头文件的定义与修改；（3）核心Initialize（）函数、Run（）函数流变计算指令的输入、偏应力核心公式（20）的编写及其公式中必要参数P、Q、m、n的准备、计算过程中的单元剪切屈服准则的代码编入、模型剪切破坏的识别及应力修正；（4）FLAC3D软件可以识别、调用的动态链接库DLL文件。在完成主要的头文件和源文件的编译和修改后，将其重新生成解决方案，并储存在Release文件夹中，命名为modelmknp.dll之后，将其拷贝到FLAC3D安装地址中的exe64文件夹中以供使用。

4 剪切流变损伤本构模型验证

4.1 计算模型

为验证本文提出的非线性软弱夹层剪切流变损伤本构模型数值模拟的正确性，选择文献[21]中室内剪切流变试验不同剪切荷载的应变时间曲线来进行对比验证，模型尺寸大小、加载条件及方式、加载时间等条件相同。数值计算的模型形状为正方体，边长为150 mm，共划分为1 000个单元、1 331个节点。具体的数值计算模型及加载条件见图4。

由图4可得，该数值模型的下半部分剪切盒全固定，不能产生位移，而对上半部施加剪切荷载，剪切荷载分5级从0.10 MPa增加到0.59 MPa，且每级剪切荷载保持的时长为34 h，上表面再施加轴向荷载，轴向荷载为0.5 MPa，由文献[21]的试验数据可知，该条件下对应的屈服强度为0.423 MPa，临界破坏时间为34 h。流变本构模型采用自定义的modelmknp模型，共进行5级不同剪切应力水平下的剪切流变数值模拟计算，对试件的顶部左侧顶点M（0，0，0.15）进行水平切向变形监测，数值试验计算采用的参数见表1。

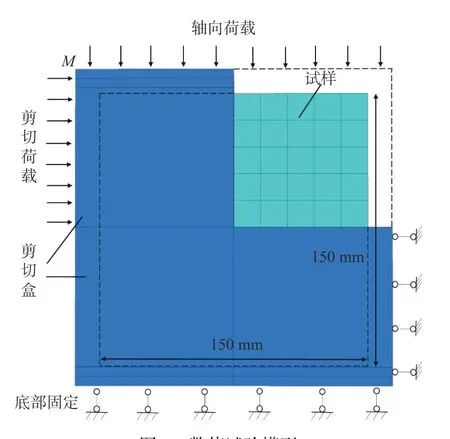
图4 数值试验模型Fig. 4 Numerical test model

表1 软弱夹层力学参数Tab. 1 Mechanical parameters of weak interlayer

4.2 数值计算结果分析

根据不同剪切应力水平下的数值模拟试验计算，获得了该软弱夹层在5级剪切荷载下的非线性流变损伤模型参数的最优组合，最优组合的确定具体为：在每一级剪切应力水平下，先通过不断模拟调整参数取值，得到一组拟合效果较好的参数组合，在此基础上，再进行参数的细微调整，得到10组模型参数组合，进行每组参数的模拟，将得到的位移时间曲线与室内试验位移时间曲线进行对比，选择曲线最接近、相关度最高的参数组合即为最优组合（表2）。

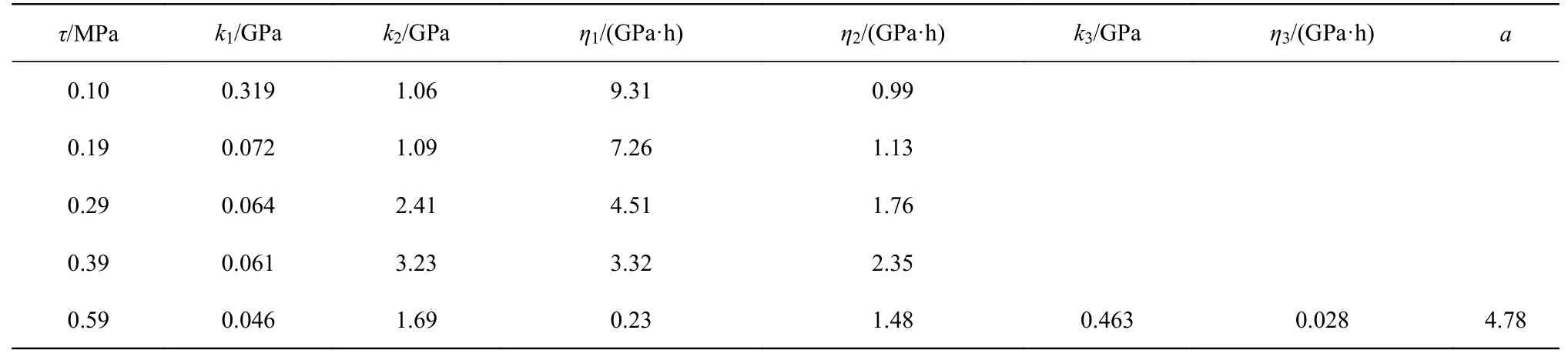
表2 不同剪切应力下流变模型参数Tab. 2 Parameters of creep model under different shear stress levels

图5 为数值模拟试验结果的塑性区分布，图中shear-p表示单元在试验过程中受剪，tension-n表示单元直到试验加载结束时受拉，tension-p表示单元在试验过程中受拉的塑性区分布情况，即上半部模型右下角单元在试验过程中受剪，而其他单元在试验过程中既有受拉也有受剪，且直到试验加载结束时受拉。

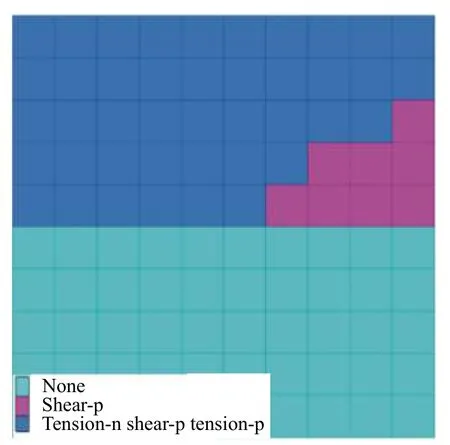
图5 数值试验结果塑性区分布Fig. 5 Plastic zone distribution of numerical test result

图6 为5级剪切应力下的试验曲线和非线性流变损伤本构模型中M点的位移曲线的对比。由图6可见，在相同的加载时长下，模型每级剪应力的应变值变化都较为接近，且每级剪应力下流变变形的变化趋势也大致相同，总体上吻合度较高，但也存在部分差异性。

图6 数值曲线与试验数据曲线Fig. 6 Numerical and experimental data curves

当施加的剪切荷载较小而未到达屈服应力，即在前4级剪切应力水平下时，其应变变形都只有减速流变阶段和稳定流变阶段，应变的变化速率先不断减小然后保持不变，应变变形量逐渐稳定，趋向于一个不变的值。而当施加的水平方向的剪切应力较大，超过其屈服应力阈值即0.59 MPa时，其应变变形阶段会历经减速过渡到稳定最后再加速共3个阶段；应变速率先减小后不变再迅速增大；应变值不断增大，不会趋于一个定值，直至破坏。对于每级剪应力下应变的增量值，其瞬时应变都较为接近，且经过相同时间的应力加载后，无论是稳定后的应变值还是加速阶段的应变值都较为接近。差异性主要表现为本文数值模拟试验在施加的剪切荷载较小而未到达屈服应力，即在前4级剪切应力水平下时得到的位移时间曲线，其减速阶段历时较室内试验减速阶段历时短，即更快地达到稳定流变阶段；而在施加的水平方向的剪切应力较大，超过其屈服应力阈值时得到的位移时间曲线，其加速流变阶段位移变化速率较室内试验位移变化速率大，且最终的位移比室内试验位移稍大。因此，可以说明本文开发的非线性剪切流变损伤本构模型是可靠的。