改善不平衡配电网电压质量的分布式储能序次优化配置方法

李英量，蔡鹤鸣，王康，孙西瑶，周丽雯，高兆迪

(西安石油大学电子工程学院，西安市 710065)

0 引 言

随着国家能源结构的改革，越来越多的可再生能源代替传统化石能源为电网提供电能。大规模新能源发电并网导致了谐波污染、电压波动、打破系统三相平衡等一系列问题，对配网的安全运行带来了极大考验[1]。新能源发电的强随机性与波动性会明显影响配电网的电压质量，易造成系统电压越限[2]。分布式储能(distributed energy storage，DES)装置具有“低充高放”、就近平抑负荷等功能特点[3]，被广泛应用于配电网的调峰、调压、降损、提供备用容量[4]等。针对分布式电源(distributed generation，DG)接入给配电网带来的电压质量问题，DES能量响应迅速，可有效服务于配电网的电压管理，提高系统接纳新能源发电的能力[5-6]。配电网通常运行在三相不平衡状态，且DES的接入会改变原始潮流分布，其接入的位置及运行方式将直接影响网络电压与网络损耗。与此同时，储能系统投运成本高昂，限制了其在电力系统中的发展[7]。为充分发挥DES在不平衡配电网中的电压管理能力，对其进行优化配置研究则必不可少。

目前，各国学者从不同角度对储能配置问题展开了广泛研究。文献[8]基于二阶锥松弛建立了储能多变量协调规划模型。文献[9]基于集群划分建立了分布式光伏与储能双层优化配置模型。文献[10]结合粒子群与精英非支配排序遗传算法，提出了混合多目标粒子群优化算法(hybrid multi-objective particle swarm optimization，HMOPSO)。上述研究均未考虑储能接入对系统电压的影响。文献[11]考虑系统电压偏差最小，建立了源、网、荷侧不同场景下的储能优化配置模型。文献[12]基于电压灵敏度等指标，构建了储能选址的多属性综合评估指标。文献[13]提出了一种加权电压灵敏度来选择DES的并网节点集，以系统净收入最大为目标建立了DES选址定容模型。文献[14]基于网损灵敏度方差确定DES的接入位置，考虑节点电压波动最小确定DES的最优配置容量。文献[15]结合储能投资的经济性建立了考虑整体节点电压偏差的储能多目标优化配置模型。上述研究均未考虑实际系统中普遍存在的三相不平衡现象，其由不对称元件及不对称负荷，以及近年来大量单相DG的接入引起。文献[16]以DES运行经济性为优化目标，提出一种含高比例DG的不平衡配电网DES优化配置方法。文献[17]同样考虑了网络的三相不平衡状态，以最大限度减小网络运营商支出为目标建立了不平衡配电网DES序次优化配置模型。但文献[16-17]同样未讨论不平衡配电网的电压质量问题，忽略了分布式储能的电压管理能力。

基于以上问题，本文以改善不平衡配电网电压水平为导向，提出一种适用DG接入的不平衡配电网DES两阶段序次优化配置策略。优化选址阶段，综合考虑不平衡配电网不同节点的不同调压需求，通过计算各节点的综合电压灵敏度方差确定DES接入位置，大大降低模型的求解维度；容量优化配置阶段，计及负荷与DG的时序特征，以最小化一次投资成本和运维成本为目标建立面向不平衡配电网的DES序次优化配置模型，并使用改进灰狼算法对该模型进行求解。基于改进IEEE 33节点三相配电网进行算例分析，验证所提DES序次优化配置策略的有效性和优越性。

1 DES优化选址模型

由于实际配电网系统中存在大量的不对称负荷与不对称元件，加上大量分布式能源的接入，进一步加重了配电网的三相不平衡状态，针对配电网的传统电压灵敏度分析已不再适用。

1.1 基于三相牛顿-拉夫逊(Newton-Raphson,N-R)潮流计算的有功-电压灵敏度分析

对于三相潮流计算，其方程数量是平衡网络模型的3倍。以a相为例有潮流方程：

(1)

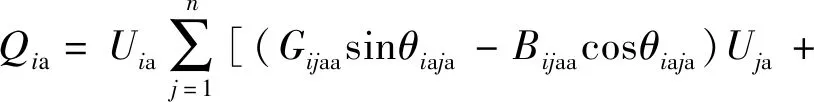
(2)

式中：n为系统节点数；Pia、Qia为i节点a相注入的有功、无功功率；Uia、Uja为i、j节点a相的电压幅值；Ujb、Ujc为j节点b相和c相的电压幅值；Gijaa、Bijaa为a相i、j节点间自导纳的实部和虚部；Gijab、Bijab为a相i节点与b相j节点间互导纳的实部和虚部；Gijac、Bijac为a相i节点与c相j节点间互导纳的实部和虚部；θiaja为i节点a相与j节点a相间的电压相角差；θiajb为i节点a相与j节点b相间的电压相角差；θiajc为i节点a相与j节点c相间的电压相角差。

由极坐标N-R潮流计算方法可得修正方程：

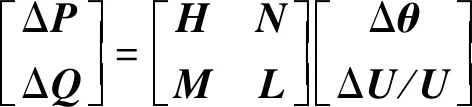
(3)

式中：ΔP、ΔQ分别为节点注入有功、无功功率的变化量；H、N、M、L为雅可比子矩阵；Δθ、ΔU/U分别为节点电压相角、电压幅值的变化量。

值得注意的是，传统雅可比矩阵中的每个元素在这里都是一个3×3的矩阵。且雅可比子矩阵N表征了P与U的耦合关系，即

ΔU=N-1ΔP

(4)

(5)

式中：N-1为节点有功-电压灵敏度矩阵；i为节点号，3i-2、3i-1、3i分别为i节点a相、b相、c相的编号；δ(3i)(3i)为i节点c相有功功率对其电压幅值的偏导数。以c相为例，其中第3i行每个元素表示其对应的各相各节点注入有功功率变化ΔP后i节点c相电压的变化情况；第3i列中每个元素表示i节点c相的注入有功功率变化ΔP后，对应各相各节点电压的变化情况。

本文主要研究DES对电压幅值的影响，且忽略其输出无功功率的能力，故使用N-1矩阵作为三相有功-电压灵敏度矩阵。传统灵敏度分析方法是依据式(6)将电压灵敏度矩阵进行列求和，以表征节点注入有功功率的变化对配电网整体电压的影响。

(6)

式中：Sj为节点j的传统有功-电压灵敏度；δij为有功-电压灵敏度矩阵中的元素。

但DES的接入改变了系统原有的电压分布，馈线上电压最高的节点有可能是DES并网点，各节点的调压需求亦发生改变。当系统中各节点的调压需求不一致时，上述传统电压灵敏度分析方法则不再适用。

1.2 三相配电网时序综合有功-电压灵敏度

为解决式(6)以直接求和的形式表示系统灵敏度无法计及不同节点有不同的调压需求，本文借鉴文献[18]的方法,将电压偏移系数考虑进灵敏度计算中。i节点m相在t时刻的有功-电压灵敏度Si,m,t可表示为：

(7)

wj,m,t=(Vj,m,t-Vref,j,m,t)2

(8)

式中：δj(3i-3+m),t为t时刻灵敏度矩阵中对应的元素值，由式(5)得出；wj,m,t为节点电压偏移系数，反映了节点调压需求的大小；Vj,m,t为t时刻相应节点的电压；Vref,j,m,t为t时刻该节点的期望电压。式(7)这一模型通过将节点电压偏移程度引入灵敏度指标中，从而区分了不同节点的不同调压需求。

综合电压灵敏度反映出系统在一定的运行方式下，节点i增加单位有功功率后对系统整体电压水平的影响。为尽可能提高DES抬升系统电压水平的效果，本文综合考虑了配电网各节点24 h的综合电压灵敏度的变化，提出基于时序综合电压灵敏度方差确定DES接入配电网位置的方法。网络中各节点的综合电压灵敏度方差为：

(9)

2 DES容量优化配置

随机性较强的新能源发电大量并网进一步加剧了系统的波动性。研究表明，储能系统凭借其灵活的功率吞吐能力可有效解决上述问题[19]。但目前储能设备的安装、维护成本相对高昂。为保证合理性与可行性，本文选取年均投资、系统运行成本及电压偏移程度为优化目标，计及功率平衡约束、系统三相不平衡度约束等运行约束建立优化配置模型。

2.1 目标函数

本文建立的DES优化模型目标函数为：

minf=CIN+COP+μDdev

(10)

式中：CIN、COP分别为储能年均一次投资成本和系统年运行成本；Ddev为系统整体节点电压偏差；μ为量纲转换系数。

1)储能年均一次投资成本CIN。

(11)

式中：η为储能设备接入数量；τ为年利率；y为储能设备运行寿命；Ce、Cp分别为储能单位容量成本和单位功率成本；EB,k、PB,k分别为第k台储能设备的额定容量和额定功率。

2)年运行成本。

COP=COM+CLOSS

(12)

(13)

式中：COM为储能设备年运维成本；CLOSS为线路损耗成本；Ploss,l,m,t为t时段第l条支路m相的损耗；L为系统总支路数；Δt为考察时段，本文取1 h；Cep为单位线路损耗成本。

3)整体节点电压偏差。

(14)

式中：Ui,m,t为t时刻i节点m相的电压；Uref为当前时段内节点额定电压。

注意到式(14)的形式为标幺化，而式(10)中其余两项均是以价格为量纲的年费用。为此，参考文献[20]将电压偏差转化为有功网损的方法，通过引入转换系数λ，结合Cep则可将Ddev转化为费用量纲。式(10)中的统一量纲转换系数为：

μ=365×Cepλ

(15)

式中：λ为有功网损与节点电压偏差转换系数，取500 kW/pu[20]。

2.2 约束条件

1)功率平衡约束。

(16)

(17)

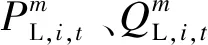
2)节点电压约束。

在所有运行方式中，系统各节点电压需在规定的约束范围内，即：

(18)

式中：Umin、Umax分别为任一时刻节点电压的最小、最大值。

3)三相不平衡度约束。

三相不平衡度是评价系统电能质量的重要指标之一，其由负序基波分量引起。根据国家标准，配电网三相不平衡度不应超过最大值εmax。

(19)

4)储能装置能量平衡约束。

考虑到DES的使用寿命，故需保证其一个周期内充放电能量守恒。

(20)

式中：PB,k,t为t时刻第k台储能设备的运行功率。

5)储能装置容量及功率约束。

受需求及预算限制，DES有容量上限Emax；而DES充放电功率受其所使用的逆变器限制，有最大值Pmax。

(21)

式中：EB,k为第k台储能设备的额定容量。

6)储能装置荷电状态(state of charge,SOC)约束。

为防止DES发生过充或过放损伤运行寿命，需要对其SOC进行约束。

(22)

(23)

式中：SOCk(t)为t时刻第k台DES的荷电状态；SOCmin、SOCmax分别为规定DES荷电状态的最小、最大值。为保证储能在一天24 h内有足够的能量，设定每台DES每天的初始荷电状态SOCk(1)为50%。

3 求解算法及求解流程

上述式(10)—(23)所描述的DES优化配置模型为典型的多约束非线性规划问题，本文借助改进灰狼优化算法进行求解。

3.1 改进灰狼优化算法

灰狼优化算法(grey wolf optimization,GWO)具有参数少、原理简单、寻优能力强等特点，被广泛应用于求解各类复杂的优化分析问题。GWO将种群分为4类：α狼——最优解、β狼——次优解、δ狼——第三优解和ω狼。其寻优过程的数学模型如下：

X(q+1)=Xs(q)-A·|C·Xs(q)-X(q)|

(24)

式中：q为迭代次数；Xs(q)、X(q)分别为q代的猎物位置和灰狼个体位置；系数A和C的定义如下：

A=a(2r1-1)

(25)

C=2r2

(26)

a=2(1-q/qmax)

(27)

式中：a为收敛因子；r1、r2均为[0,1]的随机数；qmax为最大迭代次数。

由于传统GWO算法收敛因子a为线性递减，即寻优过程的前半段与后半段a下降幅度相同，限制了算法整体上的寻优能力，遇到复杂优化问题时表现欠佳。为此，借鉴文献[21]的方法，在传统GWO的系数A中引入动态扰动因子E以改善上述弊端，其计算方式如下：

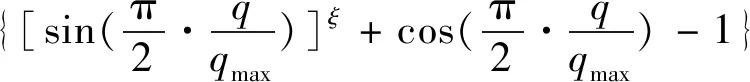
(28)

A=a(2r1-1)+E

(29)

式中：rand(·)为随机数，服从高斯正态分布；ξ为常数，决定了E的峰值位置，为进一步提升算法性能，本文取2.5[21]。

3.2 DES最优配置容量的确定

如本文第1节叙述，基于节点综合电压灵敏度方差选址的方法使改进灰狼算法无需对DES位置进行编码，大幅减小了模型的求解维度。为进一步提升求解效率，本文借鉴文献[14]的方法，仅优化DES的运行功率，计算每个DES不改变运行状态的时间段内累积的吞、吐电量绝对值，取其最大值为DES的配置容量。具体过程表示如下：

(30)

式中：Ek为第k台DES的最优配置容量；1～τ1，τ1～τ2，…，τg～τh为功率优化结果中需要连续充电的时段；1～μ1，μ1～μ2，…，μf～μp为功率优化结果中需要连续放电的时段。

3.3 DES序次配置的求解流程

1)读取系统线路参数、日负荷数据、日光伏数据，进行潮流计算并得到系统初始潮流分布；

2)设置GWO的种群数量、迭代次数等参数，并设置DES接入的数量；

3)根据式(9)计算网络各相节点的综合电压灵敏度方差，选择综合电压灵敏度方差最大的节点作为当前配置DES的接入位置；

4)初始化种群或根据式(24)—(29)更新GWO种群中个体的位置，结合潮流计算及式(10)—(15)计算所有个体的适应度值并进行比较，更新α狼、β狼和δ狼的位置；

5)判断是否达到GWO最大迭代次数，若没有达到，则返回步骤4)，否则进行步骤6)；

6)判断是否已完成DES的计划配置台数，若配置数量尚未达到，则返回步骤3)，否则继续进行步骤7)；

7)求解结束，比较不同DES配置个数下的最优目标函数值，整理并输出配置结果。

综上所述，求解本文DES优化选址定容模型的流程如图1所示。

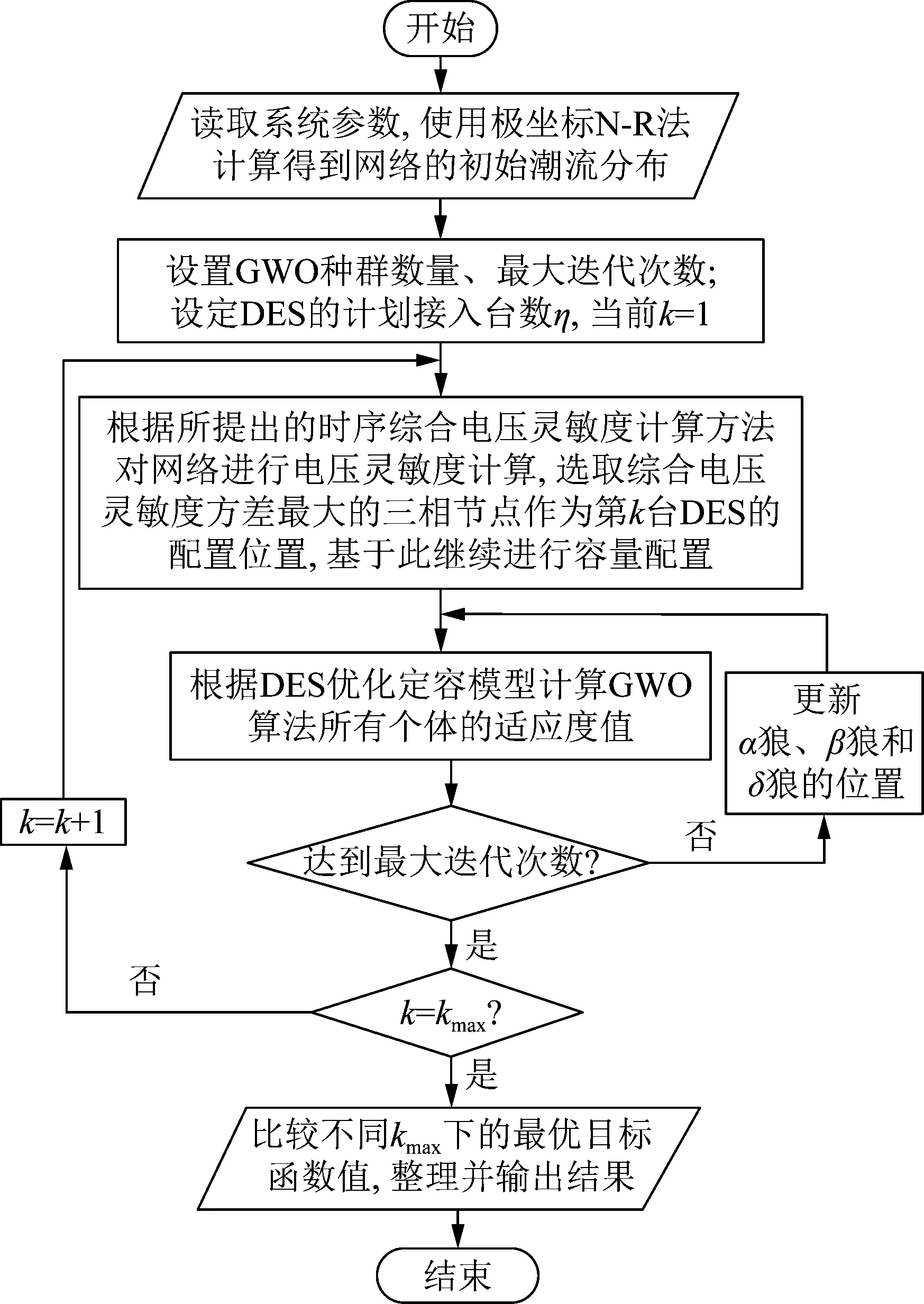
图1 DESs序次配置流程Fig.1 Flow chart of sequence configuration of DESs

4 算例分析

4.1 算例及参数设置

本文使用三相改进IEEE 33节点配电网系统对所提DES优化配置模型进行验证。系统额定电压为12.66 kV，在原算例[22]的基础上于节点11、28分别接入1 000 kW、500 kW三相光伏电源。网络拓扑结构如图2所示；典型日光伏出力曲线如图3所示。

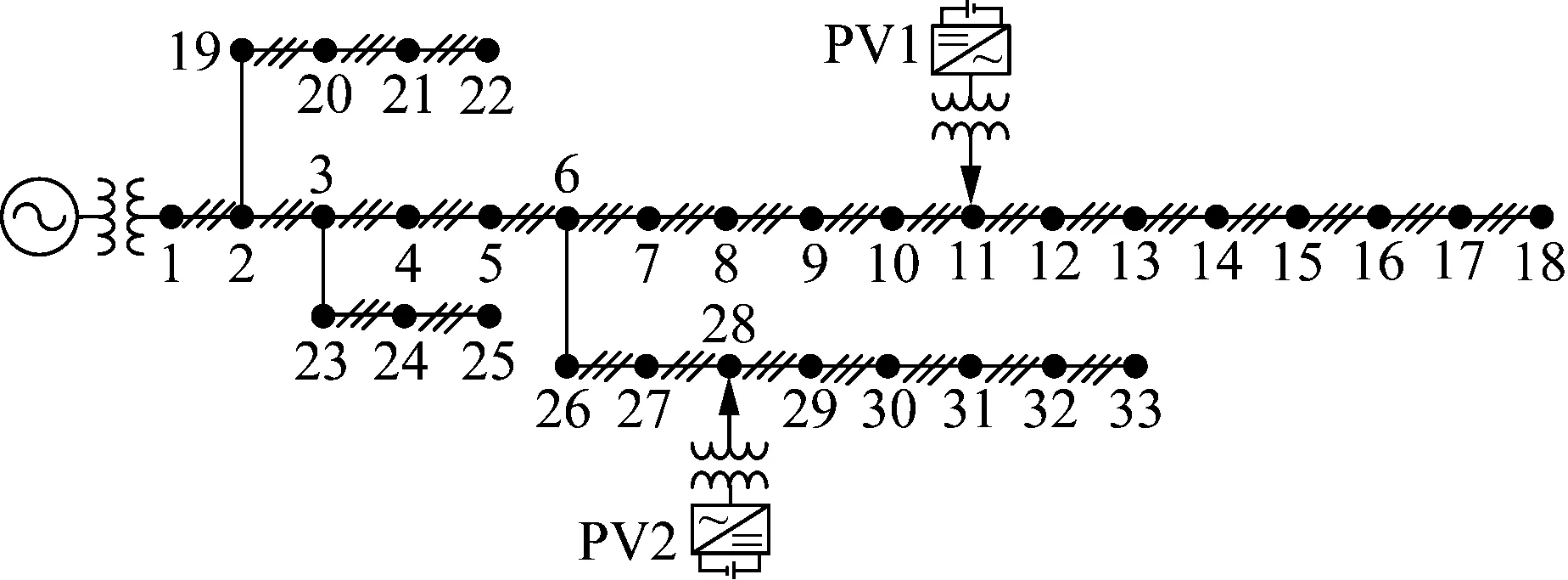
图2 改进IEEE 33节点配电网系统示意图Fig.2 System diagram of improved IEEE 33-node system

图3 典型日光伏出力曲线Fig.3 Typical daily PV output curve

三相日负荷曲线如图4所示，最大负荷为(3.634 +j2.264)MV·A。

图4 系统三相日负荷曲线Fig.4 Three-phase daily load curve

为验证所提方法的优越性，本文以下述5种场景展开算例仿真。

场景1：不接入DES；

场景2：接入DES，使用式(7)的传统电压灵敏度分析法进行选址，并采用单次计算的集中配置策略；

场景3：接入DES，使用式(7)的传统电压灵敏度分析法进行选址，并采用序次优化配置策略；

场景4：接入DES，使用综合电压灵敏度分析法进行选址，并采用单次计算的集中配置策略；

场景5：接入DES，使用综合电压灵敏度分析法进行选址，并采用序次优化配置策略。

因篇幅有限，本文将配置DES个数设为2对以上场景进行对比分析。待配置DES类型为蓄电池，其成本信息及相关约束条件参考文献[12]，具体数据见表1。

表1 仿真参数及相关约束设置Table 1 Simulation parameters and related constraint settings

4.2 仿真结果分析

基于上述场景划分及本文所提DES优化配置模型进行仿真，结果如表2和图5所示。

表2 不同场景下的优化结果Table 2 Optimization results for different scenarios

根据优化结果可知，不同场景下2台DES的功率优化结果均为0.3 MW。原因在于本模型限制了每个节点最多仅能接入1台DES，在负荷水平较高的时段为挽回节点的电压降落，DES可能需要全功率运行，均达到约束条件下的最大允许功率。优化选址方面，场景2与场景4都选择了最长的一条馈线末端的节点17、18，因采用集中配置策略，仅对系统进行了一次灵敏度计算，未能充分发挥2台DES的性能。场景2与场景4中2台DES的容量分别为1.91、1.48 MW·h和1.85、1.92 MW·h，年均成本却高达777.35万元和746.11万元，说明设备利用率低，年均成本偏高。而场景3与场景5采用序次优化配置策略，接入第1台DES后再次对系统进行灵敏度计算以确定第2台DES的选址，避免了局部配置过度，提高了设备利用率。此外，不同于场景3选择节点32作为第2台DES的最优选址，场景5使用计及节点调压需求的综合电压灵敏度分析法，识别并选取出具有更高调压需求的节点33接入第2台DES。优化结果表明场景5在接入DES容量更大的同时年均成本更小，2台DES接入容量为1.95、1.97 MW·h的情况下年均成本仅为720.81万元，印证了序次优化配置策略的优越性。

图5为不同场景下优化后的系统性能。由图5可知：本文所提DES配置策略均优于其余4种配置策略。网络损耗方面，与不接入DES相比，场景2、3、4中接入DES后单日损失的有功电量分别从3 263.1 kW·h降至2 961.9、2 522.5、2 621.5 kW·h。场景5的优化效果最好，将单日有功网损降至2 439.8 kW·h，网损优化幅度达25.2%；对电压质量的改善效果同样是场景5最优：系统单日总电压偏移量从99.44 pu降低到78.91 pu，优化幅度达20.6%；节点最大综合电压灵敏度方差从0.248 6降低到0.107 4，表明DES的最优接入从整体上有效提升了不平衡配电网电能质量，缓解了辐射型配电网末端电能质量低的情形。此外，注意到场景2中接入DES后，节点综合电压灵敏度方差出现了异常增大的情况。场景2中，a、b、c三相的节点最大综合电压灵敏度方差分别为0.272 4、0.305 7、0.293 6，均大于场景1中未配置DES时的情况。场景2采用集中配置策略，导致无法充分发挥设备性能，且对配置点附近的电压质量产生了负面影响，加剧了电压波动，使系统整体电压灵敏度方差增大。该现象也从侧面论证了本文所提序次优化配置策略的科学性。

另一方面，DES的接入实现了负荷的削峰填谷。与场景1相比，场景2、3、4中网络负荷的峰谷差分别从1 417 kW降至1 259、1 287、1 154 kW。采用本文所提方法的场景5将负荷峰谷差降至最低的883 kW，优化幅度达37.7%。图6为优化配置DES前后系统的负荷曲线。

图7为使用本文所提方法优化得出的2台DES运行情况。由图7可知，2台储能设备的工作情况及SOC曲线大致相似：系统在03：00—10：00负载水平较低，电压水平尚可，2台DES都实施充电以储存电能；12：00左右迎来当日负荷小高峰，储能设备放电以防止节点电压出现大幅跌落；14：00—17：00系统负载水平有一定降低，同时光伏出力达到当日最高，此时储能充电以保证各节点电压不越上限；之后在系统电压较低时段放电，特别是20：00前后，负荷达到当日最高水平，2台DES都全功率放电以支撑系统电压，保证各节点电压都处于合理水平。

图5 不同场景下的系统性能Fig.5 System performance in different scenarios

图6 优化前后负荷曲线Fig.6 Load curves before and after optimization

图8为优化前后网络各节点综合电压灵敏度方差。线路末端节点18在不同场景下都被选为DES待接入节点。结合图8(a)对原网络的电压灵敏度分析可知节点18处于网络末端，综合电压灵敏度方差较大，电压不稳定，易发生电压越限。图8(b)为场景5的优化结果，节点18的平均综合电压灵敏度方差仅为0.101 7，优化效果理想。

图7 场景5中两台储能装置的运行情况Fig.7 Operation state of two DESs in scenario 5

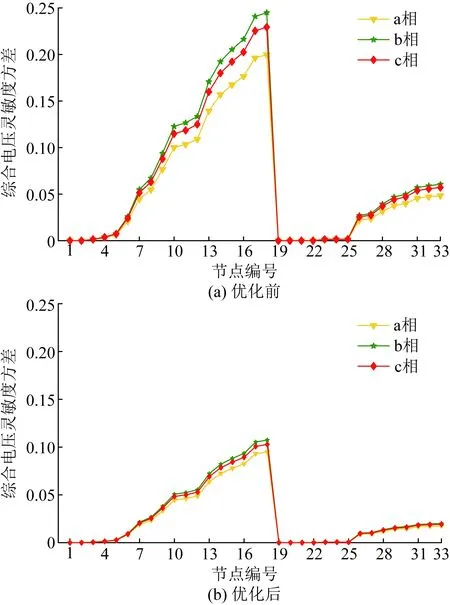
图8 优化前后网络各节点综合电压灵敏度方差Fig.8 Variance of comprehensive voltage sensitivity of each node in the network before and after optimization

5 结 论

本文针对DES如何安全可靠地接入不平衡配电网并发挥其电压管理能力展开研究。首先对系统进行电压灵敏度分析，考虑不同节点的不同调压需求，选出综合电压灵敏度方差最大的节点为DES接入位置；其次以最小年均投资运行成本为目标函数，计及时变负荷、PV接入，考虑三相不平衡度等约束建立了DES序次优化配置模型；最后使用改进灰狼算法对模型进行求解。算例仿真通过划分为5个运行场景进行对比分析，结果表明，本文所提DES序次优化配置方法相对于传统的集中配置策略能够得出更加科学的DES接入位置，对系统整体上的电压抬升效果优异。电压偏移量与电压灵敏度方差的优化效果分别达20.6%和56.8%，DES参与电压管理后系统平均节点电压偏移量仅有0.03 pu，有效改善了不平衡配电网的电压质量。同时降低了网络损耗与储能投资运行成本，兼顾经济性的同时提高了储能的实用性。