逆变型新能源场站柔性直流送出系统交流线路差动保护灵敏性优化方案

2022-01-12刘一民王书扬李彬王兴国郑少明董鹏

电力建设 2022年1期

刘一民，王书扬，李彬，王兴国，郑少明，董鹏

(1．国家电网有限公司华北分部，北京市100053；2．中国电力科学研究院有限公司，北京市100192)

0 引言

近年来，环境问题和资源问题日益突出，中国大力发展风电、光伏等新能源发电技术，新能源场站发出的电能经柔性直流输电系统与电网连接是新能源发电并网的一种重要方式[1-2]。

一方面，新能源发电机与同步电机在电磁暂态特性上的差异，给传统线路差动保护带来了很多问题[3-11]，有学者指出风电场接入后电流差动保护灵敏度有所降低[8]。文献[12-13]发现光伏的弱馈特性会造成光伏侧电流保护不能启动、差动保护灵敏度下降。针对逆变型新能源场站，文献[14]指出送出线路发生两相短路时，差动保护在并网系统为强系统时灵敏性下降，但不会拒动；并网系统为弱系统时存在拒动的风险。另一方面，柔性直流系统的接入也会对交流线路故障特征产生影响[15-20]。文献[15]指出线路两侧故障电流相位差受换流站有功和无功参考值、控制目标、过渡电阻大小、故障类型等诸多因素的影响。柔性直流输电系统具有可控性，它的接入导致交流线路电流差动保护灵敏度降低[16-17]。上述文献分别研究了新能源和柔性直流系统接入交流系统后导致线路差动保护灵敏性降低的问题，但未考虑新能源与柔性直流系统之间交流线路的情况，且未给出解决灵敏性降低的方案，因此有必要对新能源柔性直流送出线路差动保护适应性进行研究并解决灵敏度降低的问题。

本文基于逆变型新能源场站柔性直流送出系统交流线路两侧故障电流特征，对差动保护适应性进行分析，针对灵敏度降低问题，提出一种改进判据的差动保护优化方案。优化方案能够有效解决灵敏性降低问题，与降低制动系数方法相比，该方案可以通过改变参数来兼顾差动保护的可靠性，且不受新能源场站外接系统强弱影响，适用范围更广。最后，利用PSCAD仿真软件验证优化方案的有效性。

1 逆变型新能源场站柔性直流送出系统交流线路故障特征

典型逆变型新能源场站柔性直流送出系统如图1所示。本文研究对象为新能源场站出口至柔性直流系统之间的220 kV 交流线路，当线路上发生短路故障时，其短路电流由新能源场站侧和柔性直流整流站侧提供。

1.1 新能源场站侧短路电流特征

新能源场站(以逆变型电源为主)提供的短路电流特性，一方面与新能源电源的低压穿越控制策略密切相关，另一方面与主变接地方式和故障类型有关。当新能源场站采用抑制负序电流的低压穿越控制策略时，由于线路靠近新能源场站侧变压器高压侧常采取星型接地，其稳态短路电流中仅含正序电流[14]。当线路发生故障后，新能源场站提供的短路电流幅值和相角分别如式(1)、(2)所示：

(1)

βφ=θ0+φ+*+αφ

(2)

从式(1)和(2)中可以看出，新能源场站稳态短路电流三相对称，其幅值主要受有功、无功参考值影响，当电压水平跌落严重时，主要受外环限流器的限流值影响，但新能源场站提供的短路电流幅值一般不超过其额定电流的3倍[21-22]；初相角除了与上述因素有关之外，还与故障初始相角相关。

1.2 柔性直流整流站侧短路电流特征

与新能源场站相连的柔性直流换流器采取交流电压-频率控制方式，故障后柔性直流换流器呈现为电压源特征[23]，根据正序等效定则，其提供的短路电流如式(3)所示：

(3)

式中：Ef为柔性直流换流器等效内电势；ω+代表正序角频率；ω-代表负序角频率；Zeq为与短路类型有关的等效阻抗;θφ+、θφ-分别为正负序初相角；m为与短路类型有关的比例系数;iwφ为与之相连的新能源场站提供的短路电流。

从式(3)可知，柔性直流整流站提供的短路电流既有正序分量也有负序分量，且与短路故障类型相关，其中新能源场站提供的短路电流也会体现在柔性直流换流器短路电流中，这使得柔性直流换流器短路电流幅值比新能源场站提供的短路电流大很多，即相对而言，新能源场站仍有弱馈特性。

2 交流线路差动保护适应性分析

以常用的比率制动式差动保护为例分析差动保护的灵敏性，典型的差动保护判据如式(4)所示：

图1 逆变型新能源场站柔性直流送出系统拓扑图Fig.1 Topology diagram of flexible DC delivery system of inverter new energy station

(4)

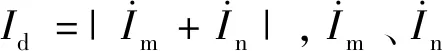
2.1 相间短路故障

以AB两相短路故障为例分析差动保护灵敏性，结论也适用于其他类型两相短路故障。

(5)

柔性直流整流站侧短路电流相位：忽略线路电容电流情况下，由基尔霍夫电流定律可知：

(6)

又新能源侧短路电流三相对称，因此式(6)可进一步简化为：

(7)

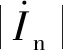
图2 AB两相相间故障时线路两侧故障相电流相量图Fig.2 Phasor diagram of fault phase current on both sides of line under phase-to-phase fault between A and B

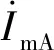
2.2 不对称接地故障

以AB两相接地故障为例分析差动保护适应性，结论也适用于其他类型接地故障。当送出线路发生区内AB两相短路接地故障时，受零序电流分量影响，新能源侧AB两相电流相角差不再等于120°，柔性直流侧AB两相的短路电流相角差也不再等于180°。

故障点两侧零序等值阻抗均由线路零序阻抗和其主变零序阻抗组成，若忽略两侧变压器零序阻抗差异，则可认为两侧零序等值阻抗相等，因此送出线路两侧提供的零序电流分量相位相同，减小了两侧短路电流之间的相角差。同时两侧提供的短路电流受限流控制影响，短路电流零序分量相对占比增加，进一步削弱了控制策略对两侧短路电流相角差的影响。因此，送出线路发生不对称接地故障时两侧故障相电流相角差不会出现大于90°的情况，差动保护能可靠动作。

2.3 对称短路故障

当交流线路发生区内对称短路故障时，两侧故障相电流均无零序分量。新能源场站侧只提供正序电流，三相电流相位互差120°；柔性直流整流站侧的三相电流相位互差也近似为120°。分析结果与相间短路故障类似，区别在于当两侧A相电流相角差出现超过90°情况时，B相电流相角差也会超过90°。

3 差动保护灵敏性优化方案

3.1 改进判据

从第2节的分析中可知，新能源场站经柔性直流系统接入电网，当交流线路发生两相相间或者对称短路故障时，可能会出现两侧短路电流相角差超过90°的情况，此时差动保护灵敏度降低。为了解决灵敏度降低问题，本文提出了一种改进判据的差动保护方案，改进后的判据如式(8)所示：

(8)

式中：a=Bcos(180°-θmn)，其中0≤B≤1，θmn为两侧电流相量之间不超过180°的夹角(0°≤θmn≤180°)。

改进之后的差动保护判据，其制动分量与a的取值有关，区外故障或者正常运行时，有θmn≈180°，此时制动分量达到最大，差动保护可靠不动作；当区内故障且0°≤θmn<90°时，有a<0，此时制动分量取为0，即区内故障时制动分量为0，提升差动保护的灵敏性；当区内故障且90°≤θmn<180°时，有a≥0，此时制动分量取为Bcos(180°-θmn)Ir，削减相角差超90°带来的灵敏度降低程度。

3.2 保护性能对比

工程上常通过降低比率制动系数k值来提高差动保护灵敏性，但是它同时也降低了保护的可靠性。本文分别选取B=0.8和B=1.0两种情况来与制动系数为k=0.8的常规差动保护进行灵敏性和可靠性对比。

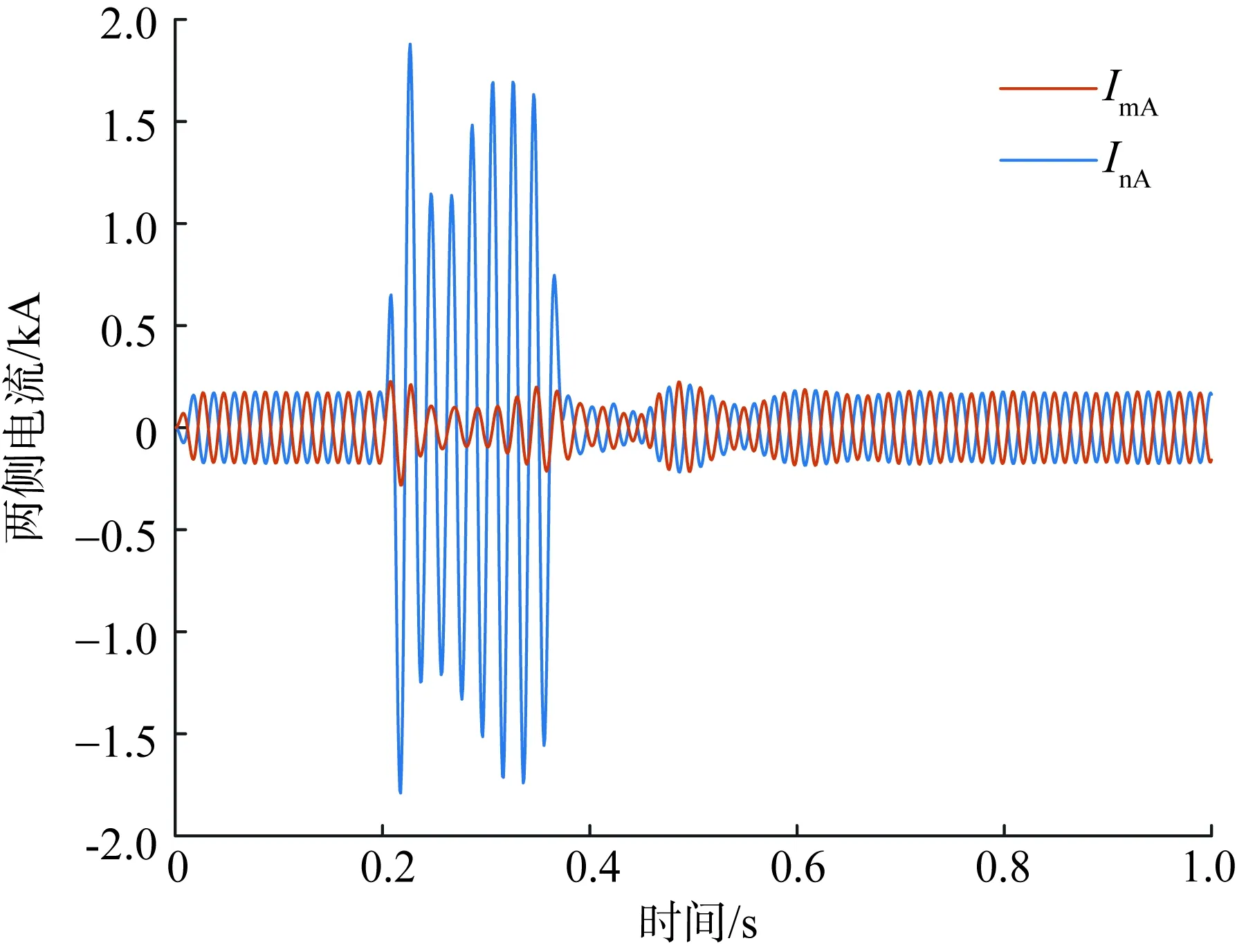
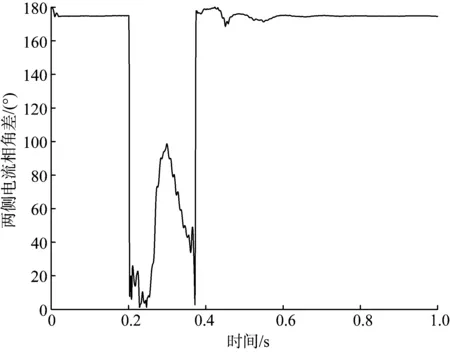
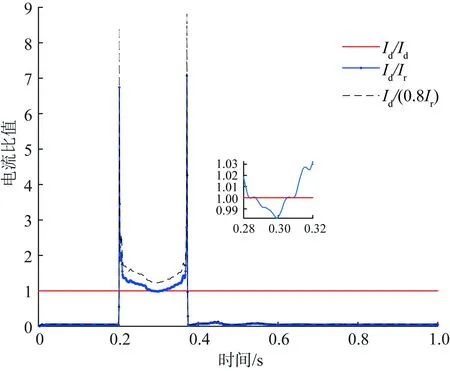
1)B=1.0。当B=1.0时，a=cos(180°-θmn)。正常运行或发生区外故障时，有θmn≈180°，a=1，制动分量为Ir，比常规差动保护的制动分量0.8Ir更大，保护更不易误动，可靠性更高；当发生区内故障时，当0°≤θmn<143.13°时，a<0.8，改进判据的制动分量小于常规差动保护的制动分量，改进判据差动保护更不易拒动，灵敏性更高；当143.13°<θmn≤180°时，有0.8

2)B=0.8。当B=0.8时，a=0.8cos(180°-θmn)。正常运行或发生区外故障时，有θmn≈180°，a=0.8，改进判据差动保护制动分量与常规差动保护的制动分量一样大，两者可靠性相同；发生区内故障时，无论θmn的大小，始终有a≤0.8，改进判据的制动分量始终小于常规差动保护的制动分量，区内故障时改进判据的差动保护更不易拒动，灵敏性更高。

由上可知，改进判据可以根据两侧电流相角差的情况选择适当B值来兼顾差动保护灵敏性和可靠性，只要满足B≥k改进判据区外故障可靠性就会高于常规差动保护，特别地当B=k时，其可靠性与常规差动保护一样，但是其在区内故障灵敏性始终高于常规差动保护。

4 仿真验证

4.1 仿真系统

在PSCAD软件上搭建某新能源场站接入张北四端柔性直流系统模型，如图3所示。其中逆变型新能源场站采取抑制负序电流的控制策略，柔性直流换流器采用孤岛控制模式，送出线长10 km，线路上设置5个故障点，其中F2、F3和F4是区内故障点，F1和F5为区外故障点。在满载工况下模拟线路区内外各种故障(故障起始时刻为0.2 s，持续150 ms)。

图3 仿真模型示意图Fig.3 Schematic diagram of simulation model

4.2 故障特征验证

满载工况下F2点发生两相相间(AB)故障，仿真得线路两侧A相电流波形如图4所示。

图4 F2点AB相间故障时线路两侧A相电流Fig.4 Currents in phase A on both sides of the line in case of phase-to-phase fault at F2 between A and B

由图4可以看出，AB相间故障期间柔性直流整流站侧的A相电流在故障后22.67 ms达到峰值1.88 kA，新能源场站侧A相电流在故障后7.50 ms达到峰值0.226 kA，符合新能源场站侧短路电流呈现弱馈特征的分析。

对两侧A相电流夹角进行分析，夹角θA选取的是2个相量之间相隔的角度(0°≤θA≤180°)。AB相间故障期间两侧A相电流夹角情况如图5所示。

图5 F2点AB相间短路故障下两侧A相电流夹角Fig.5 Angle difference of two-end currents in phase A under phase-to-phase fault at F2 between A and B

从图5中可以看出，非故障期间两侧A相电流夹角接近180°，故障期间两侧A相电流夹角最大达到了98.37°，出现了大于90°的情况，此时Id/Id、Id/Ir和Id/(0.8Ir)三者大小关系如图6所示(Id为差动电流、Ir为制动电流、0.8Ir为制动分量)。

图6 F2点AB相间短路故障下三种电流比值Fig.6 Three current ratios under phase-to-phase fault at F2 between A and B

从图6小窗中可以看出，差动电流Id出现小于制动电流Ir情况，此时两侧A相电流夹角超过90°，但是制动分量0.8Ir(虚线)仍小于差动电流Id，制动系数为k=0.8的差动保护不会发生拒动，与理论分析一致。

4.3 改进方案性能验证

改进判据之后的差动保护在B=1.0和B=0.8两种情况下与制动系数k=0.8的差动保护在F2点AB相间短路故障时的制动分量以及故障时的差动电流如图7所示。

图7 F2点AB相间短路故障下各分量对比Fig.7 Comparison of each component under phase-to-phase fault at F2 between A and B

从图7中可以得到，正常运行时，改进判据B=1.0的差动保护制动分量最大，保护可靠性最高，改进判据B=0.8的差动保护制动分量与制动系数k=0.8的差动保护制动分量相等，两者保护可靠性一致，三个制动分量均大于差动电流，保护可靠不动作；区内故障时，改进判据B=0.8制动分量最小，保护灵敏度最高，B=1.0的差动保护制动分量也小于制动系数k=0.8的差动保护制动分量，前者保护灵敏度也高于后者，与理论分析一致。