瓦斯爆炸冲击波对通风设施破坏情况数值模拟影响因素分析

陈德勇 贺小轩 杨 慧 相光友 左祖雄

(1.阿勒泰正元国际矿业有限公司，新疆 阿勒泰 836700；2.中国矿业大学(北京)应急管理与安全工程学院，北京100083；3.中国节能环保集团有限公司，北京100082)

0 引言

瓦斯爆炸事故后果严重，事故发生后均有以下特点：矿井通风构筑物几乎全部被摧毁，通风系统遭到严重破坏，通风紊乱导致灾情迅速扩大到井下其他区域；由于有毒有害气体浓度大、缺氧、温度高等原因，使得救援队伍救援难度巨大。

许多学者研究空中、水下、近地面附近爆炸冲击波的破坏作用及其影响因素，如王莹等基于实验和数值模拟方式研究水中爆炸冲击波载荷对冰层破坏的影响因素，总结出主要影响因素是爆距、药量、冰厚；姚成宝等基于LS-Dyna软件模拟爆炸冲击波在空气中的传播过程，讨论网格密度和边界条件对计算结果的影响，结合相关实验结果，验证数值模拟结果的有效性；徐景德、蔺照东基于数值模拟方法，系统研究井下巷道瓦斯爆炸冲击波传播的影响因素。基于研究现状可知，对金属板在受限空间内爆炸冲击载荷的破坏作用的研究较少，而且极少涉及到冲击波在固体结构内传播作用过程。由于爆炸试验危险性较大，且代价较为高昂，采用数值模拟方法研究气体爆炸问题，是基于计算流体力学、爆炸力学、化学动力学和气体爆炸理论等方面的研究成果开展的。数值模拟方法可以节约实验成本，因此受到人们重视。

本文研究爆炸冲击波在井下受限空间内传播过程中对通风设施破坏作用的影响因素，模拟单条巷道中瓦斯爆炸传播的情况，研究爆炸总能量、通风设施厚度、边界条件等因素对破坏作用的影响。

1 建立数值模拟模型

基于LS-Dyna有限元分析软件，建立多种矿井巷道数值计算模型，使用ANSYS Workbench中的Geometry建立物理模型，模型建立时，考虑到巷道具有对称结构，因此巷道可以采用1/2或1/4的模型进行建模，可以极大地节省计算资源。整体分解图(如图1)，左侧部分为爆炸混合气体，中间部分为空气域，长度固定在10m，截面积不小于16m，右侧部分为风门。

图1 有限元模型

在ANSYS参数化设计语言(ANSYS Parametric Design Language，APDL)前处理中，瓦斯空气混合气体、空气、风门均选择solid164实体单元，将材料参数Null赋给瓦斯空气混合气体和空气，材料参数Plastic_Kinematic赋给风门。其中瓦斯空气混合气体和空气采用Liner Polynomial状态方程来描述，具体参数，见下表。

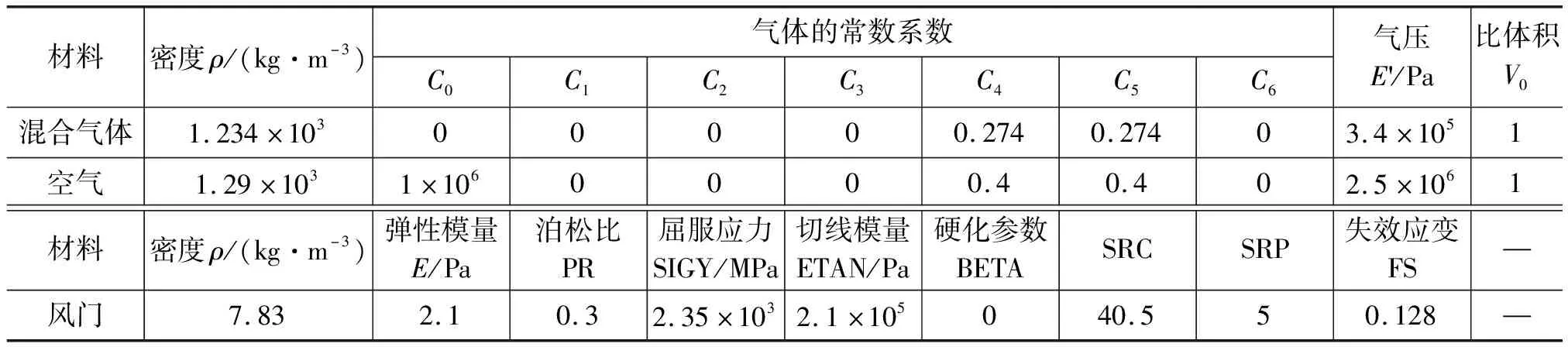
表 材料参数

注：BETA介于0到1之间；SRC为参数

C

的应变率，此值如果为0则不考虑应变率效应；SRP为参数

P

的应变率。

风门所采用的Plastic_Kinematic材料模型是一种各向同性、随动硬化混合模型，如图2本构模型所示，其与材料本身应变率相关，可以考虑失效，且参数容易确定。通常用Cowper-Symonds模型来描述应变率效应对屈服强度的影响，方程为：

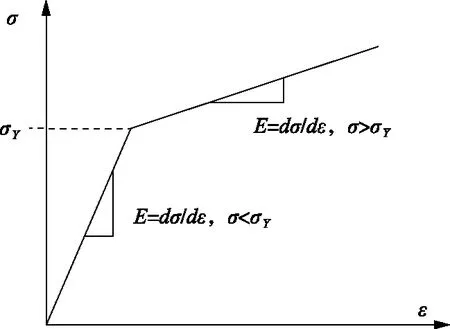
图2 Plastic_Kinematic本构模型

(1)

式中：

σ

—屈服强度，MPa；

C

、

P

—Cowper-Symonds应变率参数；

ε

—应变率；

σ

—初始屈服应力，MPa；

E

—塑性硬化模量，MPa；

β

—硬化系数，在[0，1]取值。

2 不同工况条件下瓦斯爆炸冲击波动态响应特征

2.1 不同体积气体爆炸冲击波对风门的动态响应特征

在实际事故中，由于瓦斯集聚与空气混合形成的混合气体处在爆炸极限内，遇到足够的点火能就会发生爆炸反应，爆炸产生的冲击波强度与爆炸的混合气体体积具有一定关系，在方形巷道内，可燃气体距离风门8m的距离，通过改变混合可燃气体的体积，设置0.6、1.2、2.4m3个体积梯度，研究风门上动态响应的变化。

风门上的速度、位移、总能量的变化情况,如图3。从图3(a)可以看出，2.4m的混合爆炸气体爆炸产生的冲击波最先作用到风门上，其次是1.2和0.6m混合爆炸气体，到达时间分别为1 973、2 273、2 673μs。在加速过程中，2.4m混合爆炸气体产生的加速度最大曲线较陡，但是冲击波作用在风门上的时间最短，0.6m混合爆炸气体产生的加速度最小曲线较缓，但是冲击波作用时间最长，综合来看0.6m混合爆炸气体对风门在速度上的作用最大，其次是1.2和2.4m混合爆炸气体。从图3(b)可以看出，速度达到一定程度后，风门才会开始出现位移，在A线上可以看出前期速度较小，斜率上有一个加速过程；在4 500μs之前是C情况产生的位移大，之后则是A情况产生的位移大。从图3(c)可以看出风门上总能量的变化情况，主要是动能上的差别，A情况下风门上的动能最大，其次是B、C情况，当动能达到最大后，有一部分单元达到失效条件，逐渐开始失效结构发生破坏，然后被删除不参与后续的计算，因此动能会有一个较大的衰减，但是剩余单元仍保持较大速度，没有大幅衰减。

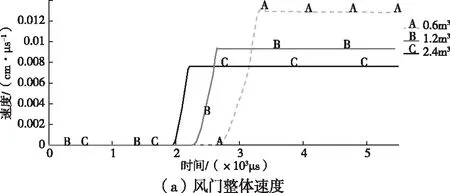
图3 不同体积爆炸气体下风门速度、位移、总能量的时间曲线

2.2 爆炸冲击波对不同厚度风门的动态响应特征

在实际应用中，风门的厚度略有不同，本例中以圆形通风巷道为例，分别计算3和6cm厚度风门在爆炸冲击波作用下的动态响应过程。不同厚度风门的速度、位移、能量变化，如图4。从图4(a)可以看出，6cm厚度的风门速度小于3cm厚度的风门，即厚度小的风门上单元获得的速度更大；从图4(b)可以看出，6cm厚度的风门位移小于3cm厚度的风门，即厚度小的风门上单元的位移更大；从图4(c)可以看出，6cm厚度的风门动能小于3cm厚度的风门，B情况出现2次衰减，主要是因为6cm厚度风门单元有2次大范围失效，能量损失的也更多。

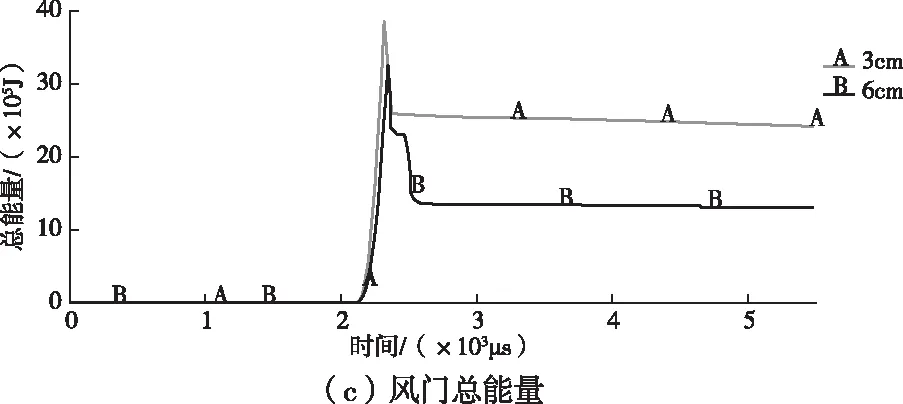
图4 不同厚度风门的速度、位移、能量变化图

2.3 爆炸冲击波对不同约束条件下风门的动态响应

在实际应用中，不同巷道根据不同的实际需求会设置不同的边界条件，对于永久封闭的风门可以采取四边固支的方式，对于正在使用的风门可以采取左右两边固支上下两边简支的方式，针对设置的不同边界条件采用方形巷道进行计算，其他条件固定不变，研究不同边界条件下方形风门的动态响应和破坏过程。

四边固支和两固支两简支的风门在爆炸冲击波作用下的速度、位移、能量变化的时程曲线，如图5。图5(a)中在3 000μs前A情况和B情况风门速度增加过程一样，固支边与巷道固接，四边固支的情况对风门速度的增加阻力更大，两边简支两边固支的情况简支边阻力较小，就使得风门获得更高的速度；图5(b)中2种情况位移的差距是因为风门速度的不同引起的，B情况的风门在冲击作用下产生的位移更大，相对A情况来说局部的破坏情况会更严重；图5(c)是风门总能量的变化情况，主要是取决风门单元整体的速度变化情况，B情况下风门获得的动能大于A情况，从曲线的衰减过程可以看出B情况下单元失效损失的动能更多，即B情况下结构的失效情况会更严重。

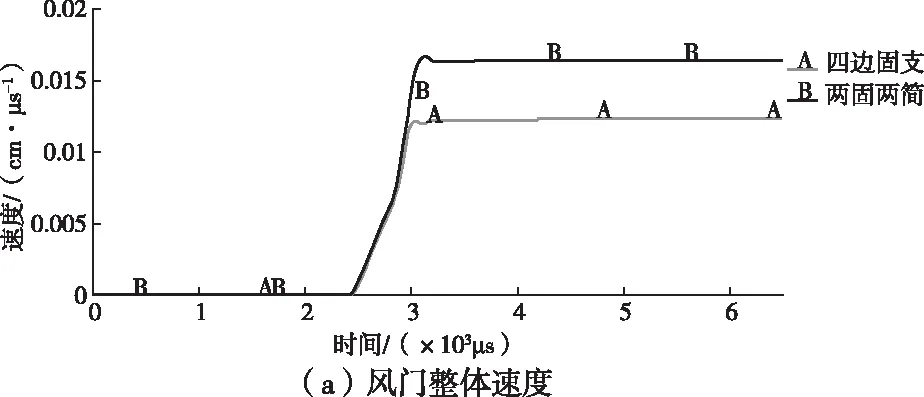
图5 不同边界条件下风门的速度、位移、能量的时间曲线

综上可知，爆炸气体体积不同的情况下，爆炸气体体积越大，最早接触风门，但作用的时间短，对风门速度作用小，风门最终产生的位移越小，风门的动能也越小。风门厚度不同时，风门厚度越小，风门获得的速度越大，单元位移更大，动能也越大。约束条件不同时，两边简支两边固支较四边固支产生的阻力小，因而获得的速度大，破坏情况会更严重。横向对比3种情况下风门的动态响应特征可以看出，爆炸气体的量的改变对风门上获得的能量影响最大，其次是风门采用的边界条件，固支或简支引起风门上能量变化较大，风门的厚度对获得能量的影响最小。

3 不同工况条件下瓦斯爆炸冲击波动态破坏特征

3.1 不同体积气体爆炸冲击波对风门的动态破坏特征

如图6所示，分别为3种不同体积的混合爆炸气体作用下风门在5 500μs的位移和速度分布图形，结合图3可以看出，图6(a)(b)为0.6m混合爆炸气体作用下风门的位移和速度分布图，从中可以看出风门结构的裂缝更为明显，大体上分布在风门中部，三横一纵的形状，风门右边2个角上破坏程度较大，风门表面均有不同程度的细小破坏；图6(c)(d)中可以看出裂隙轮廓大于0.6m的情况，呈现两横一纵的形状，风门右边2个角上与裂隙的交汇处破坏程度较大；图6(e)(f)为2.4m混合爆炸气体作用下位移和速度分布图，风门裂隙主要集中分布在边框附近，呈现多条横向和纵向的裂缝，风门中部较为完整。

图6 不同体积爆炸气体下风门的位移和速度分布图

3.2 爆炸冲击波对不同厚度风门的动态破坏特征

如图7所示，以圆形风门为例进行计算，图7中深色区域是位移或速度集中的地方，同一个算例中位移和速度的分布是相关的，3cm厚度的风门已经发生明显的变形，从中心到圆周，速度和位移呈梯度分布，差值较大的地方出现多圈环向的裂缝，中部深色区域结构破坏严重；6cm厚度的风门位移和速度集中在中部和圆周附近，2个位移较大的部位之间还存在环向的位移较小的部位，呈现出W型的位移变化情况，总的来说在5 500μs内，6cm厚度的风门破坏程度小于3cm厚度的风门。

图7 不同厚度风门的位移和速度分布图

3.3 爆炸冲击波对不同约束条件下风门的动态破坏特征

2种不同边界条件下，风门在爆炸冲击波的作用下，结构开始失效的位置都是从四角开始，一直到表面单元全部失效。不同的是失效的过程，四边固支情况下最先产生四边的失效和横向上的失效；两边固支两边简支是从四角均匀扩散，最先产生纵向上的失效，风门上的裂缝都是随着失效区域产生的，所以失效的过程不同，产生的裂缝也不同。四边固支情况下的裂缝随着固支边附近产生裂缝，形成一个小的四边形的裂缝，并在中间有一个横向的贯穿裂缝；两固两简在中间形成X型的裂缝，并在左右两边产生一个横向上贯穿裂缝。2种不同边界条件下风门整体的速度和位移分布(如图8)，四边固支情况下风门边框位移和速度均为零，固支风门四周的位移较小，中部整体的位移较大，这使得中部与四周之间出现较大的位移差，形成裂缝，越向内速度和位移越大；两边固支两边简支的风门整体的位移较大，四角位置位移最小，越向中部速度集中的区域，位移也最大，整个风门呈现一个向内凹的形状，位移和速度的分布是相关的。

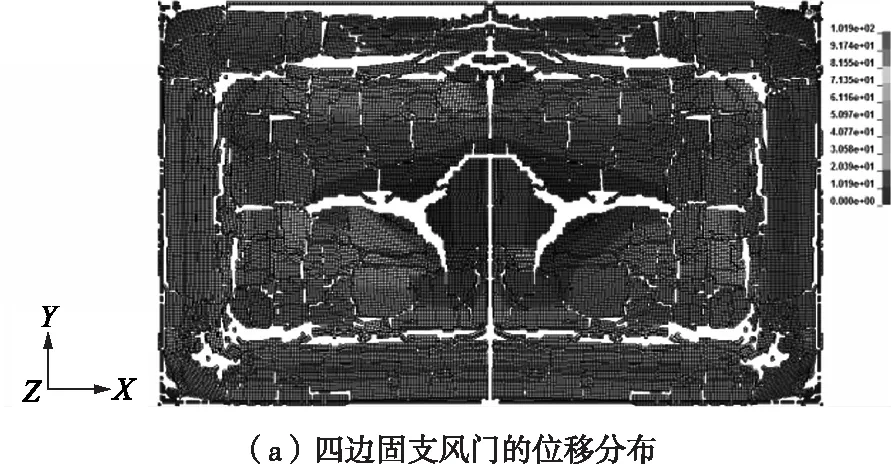
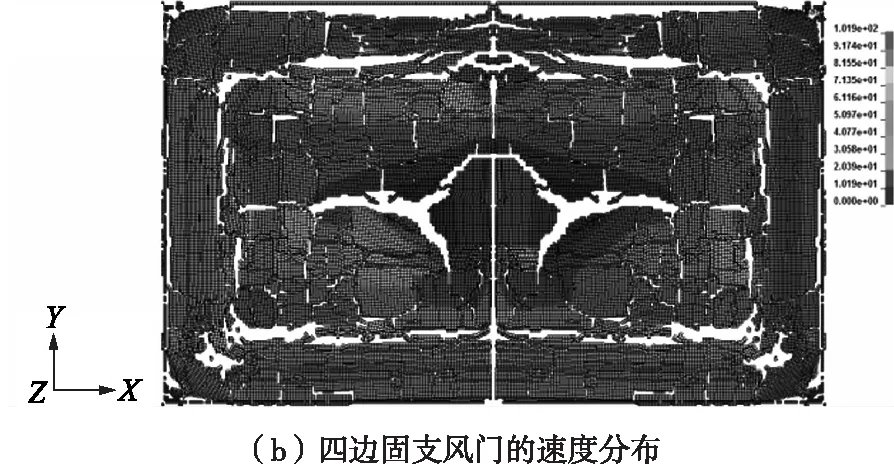
图8 不同边界条件下风门的位移和速度分布图

综上可知，爆炸气体体积不同时，爆炸气体体积越小，风门的结构裂隙越明显。风门厚度不同时，风门厚度越小，风门形变更加明显。约束条件不同，失效过程不同，产生的裂缝位置也不同，内部位移也不同，固支风门中部整体的位移较大，而两边固支两边简支的风门整体的位移较大。

4 结论

(1)瓦斯爆炸冲击波在井下受限空间内对通风设施的破坏作用的影响因素主要包括爆炸总能量、通风设施厚度、边界条件这3类。通过建立多种数值建设模型模拟单条巷道中瓦斯爆炸传播的情况，避免爆炸危险，并得到3类因素对破坏作用的影响大小。

(2)通过模拟运算，得出爆炸气体体积越大的工况对空气的加速度越大，冲击波最先接触风门，但作用时间更短，传递给风门的能量最小，产生的破坏情况也最轻；对于厚度小的风门在冲击波作用下会获得更大速度、位移、能量，因此被破坏的情况更加严重；固支的边界条件下，风门获得的速度、产生的位移小于简支的边界条件，风门的破坏形成的断裂与边界条件有关。横向比较可知，对风门获得能量影响作用从大到小依次是爆炸气体的体积、边界条件、风门厚度。

(3)不同的工况瓦斯爆炸冲击波对风门的破坏特征不同，根据数值模拟结果来看，爆炸气体体积越小，裂隙越明显，风门厚度越小，形变越明显，失效过程、裂隙位置、内部位移与不同的约束条件有关。