主轴运行状态下机床刀尖点动力学行为分异特征辨识

马维贞，胡 腾,2，郑华林，李 湉

（1.西南石油大学机电工程学院，四川成都 610500；2.石油天然气装备技术四川省科技资源共享服务平台，四川成都 610500；3.中国航发航空科技股份有限公司，四川成都 610500）

切削颤振严重制约着切削效率和表面加工质量，亦是产生机床故障、刀具磨损等问题的主要原因［1-3］。目前，基于时滞动力学方程特征值问题的切削稳定性叶瓣图绘制是预测切削颤振的有效手段之一，而机床刀尖点动力学行为参数是切削稳定性叶瓣图绘制过程中极为重要的输入变量［4-5］。研究表明［6-9］，在高速铣削过程中，由于主轴系统受到离心力、陀螺力矩、轴承热预紧等高速效应的作用，机床刀尖点动力学行为随转速变化而产生分异，进而改变机床切削的稳定性。为此，如何有效、准确地掌握刀尖点动力学行为及其分异特征已经成为切削稳定性精准预测中亟待解决的关键共性问题，对其进行研究具有重要的科学意义与工程价值。

针对刀尖点动力学特性及其影响因素，国内外学者进行了较为深入的研究。Iglesias等［10］基于输出响应数据对刀尖点动力学行为进行了准确的预测。Peng等［11］结合工作模态分析和实验模态分析，提出了一种计算刀尖点频响函数的新方法。Matsubara等［12］进行了冲击实验，提出了一种在主轴转速变化条件下刀尖点频响函数的预测方法。Deng等［13］利用有限元方法获取了机床刀尖点的频响函数，结果表明，基于Kriging模型的方法可以预测不同空间位置的切削稳定性。刘宇等［14］基于导纳综合法提出了立铣加工刀尖点动态特性的预测方法。闫蓉等［15］着重分析了铣削系统子结构之间结合部的建模和参数辨识的问题，采用子结构响应耦合方法预测刀尖点频响函数，获取了不同刀具-刀柄组合所对应的刀尖点频响函数。Cao等［16］通过对高速工况下的主轴进行动力学建模，提出了一种获得与转速相关的刀尖点频响函数的方法。

不难看出，在现阶段针对主轴运行状态下刀尖点动力学行为的研究主要借助实验检测或数字化分析。实验研究可以避免复杂的理论建模［10-12］，但测试设备昂贵，实验成本过高；而对于以数字化分析为基础的理论研究［13-16］，除了建模过程繁复之外，在数据预处理和结果验证阶段亦须耗费大量计算成本，且结果的精确程度依赖于模型的准确性和完备性；此外，部分学者提出了实验与数值建模相结合的半理论方法，但在研究过程中鲜有考虑刀尖点的刚度对其动力学行为分异特性的影响［17-18］。

为此，本文以某立式加工中心为研究对象，以频域零阶近似法为切削稳定性预测理论基础，考虑在主轴运行状态下刀尖点刚度的变化，提出一种基于半理论法的主轴运行状态下刀尖点动力学行为分异特征辨识方法。该方法将分异特征辨识转化为一类优化设计问题，即以不同转速下刀尖点动力学特性参数为变量、以极限切深和颤振频率的实验标定值与理论预测值的偏差之和最小为目标构建优化模型，借助粒子群退火优化算法对其进行求解，从而获取在不同转速下刀尖点动力学行为的分异特征及规律。

1 基于半理论法的辨识原理

1.1 基于频域零阶近似法的切削稳定性预测

Budak等［19］提出的轴向极限切深ɑlim和颤振频率ωcha为：

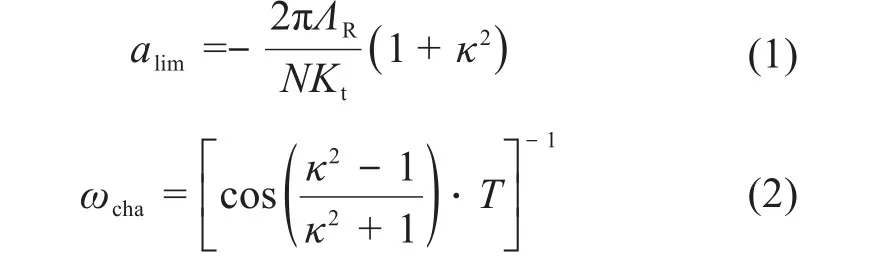
以刀尖点x向的频响函数Gxx为例，利用固有频率ω、阻尼比ζ和刚度k可将其表示为：

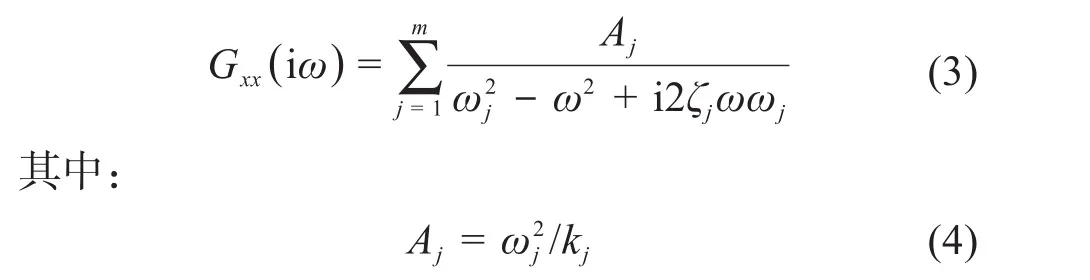
式中：j为模态阶数，j=1，2，…，m；i为虚数单位。

1.2 刀尖点动力学特性优化辨识

刀尖点动力学特性参数共有6个。由1.1节可知，极限切深ɑlim和颤振频率ωcha均为刀尖点非对称动力学特性参数的函数，即：

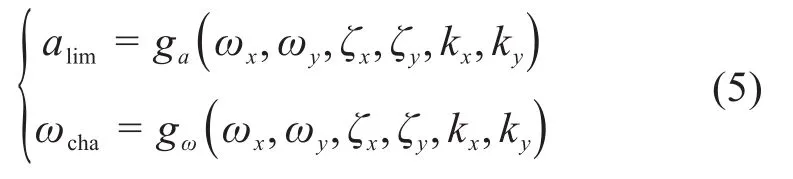
式中：ωx、ωy、ζx、ζy、kx和ky分别为刀尖点x和y方向的固有频率、阻尼比和刚度。

利用主轴静止状态下（即n=0 r/min）刀尖点动力学特性参数，可对其极限切深alim_pre（0）和颤振频率ωcha_pre（0）进行预测，但所得结果并未考虑刀尖点动力学行为随转速变化的分异特征；利用主轴运行状态下（n≠0 r/min）刀尖点动力学特性参数，则可以预测考虑分异特征的极限切深alim_pre（n）和颤振频率ωcha_pre（n）。此外，通过变切深切削噪声测试，可以对不同转速下实际极限切深alim_cal（n）和颤振频率ωcha_cal（n）进行标定。所得标定结果是对不同转速下切削过程的真实反映。

因此，为准确辨识刀尖点动力学行为随转速变化的分异特征，基于半理论法，结合理论预测与实验标定结果，将不同转速下刀尖点动力学特性参数的辨识问题转化为如式（6）所示的优化设计问题：

式中：Θn为待求优化变量，即在转速n下的刀尖点动力学特性参数：

式中：ea(n)、ew(n)分别为极限切深、颤振频率的实验标定值与理论预测值之间的偏差，即：

利用粒子群退火优化算法［20］求解上述优化模型，获取式（8）中各变量的最优解，亦即辨识在不同主轴转速下刀尖点动力学行为分异特征。

由上所述，可建立在不同主轴转速下刀尖点动力学行为分异特征辨识方法，如图1所示。

图1 刀尖点动力学行为分异特征辨识方法Fig.1 Identification method of dynamics behavior differential characteristic of tool tip

2 算例与验证

2.1 立式加工中心刀尖点动力学行为分异特征辨识

2.1.1 刀尖点锤击模态实验

在VMC850立式加工中心上进行刀尖点锤击模态实验，以获取静态刀尖点动力学特性参数。刀尖点锤击模态实验平台如图2所示。其中刀具选用硬质合金方肩铣刀，其直径D=20 mm，刀具齿数Z=2。实验测得刀尖点在x、y向的前4阶模态参数，如表1所示。

表1 刀尖点模态参数（n=0 r/min）Table 1 Tool tip modal parameters（n=0 r/min）

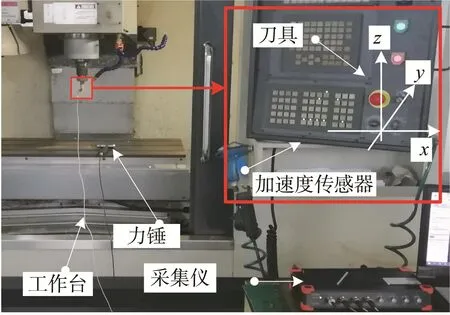
图2 刀尖点锤击模态实验平台Fig.2 Tool tip hammering modal experimental platform

2.1.2 基于切削噪声测试的切削稳定性标定

在VMC850立式加工中心上搭建切削噪声测试平台，如图3所示。采用GRAS 46AE自由场麦克风采集不同转速下变切深切削噪声。工件材料为AL 7075-T6，其沿y向正向进给铣槽。实验中，径向切宽ae和进给速度 v保持恒定（ae=20 mm，v=200mm/min），轴向切深ap=0～8 mm，进给行程l=120 mm，设置主轴转速n=3 000，3 300，4 000 r/min。通过分析切削噪声信号的时频特征，结合主轴转速、刀具齿数及锤击模态实验所得的静态刀尖点动力学特性参数等信息，可对实际颤振频率ωcha_cal（n）进行甄别与标定；此外，通过对工件加工表面振纹出现处的轴向深度的测量，可对实际极限切深alim_cal（n）进行标定。

图3 切削噪声测试平台Fig.3 Cutting noise test platform

当n=3 000 r/min时变切深铣削实验结果如图4所示。由图4（a）的时域信号可知，切削噪声的声压在第28秒左右发生突变，其幅值显著增大，说明在实验过程中存在不稳定切削；由频域信号可知，切削噪声突变部分的主频成分为1 178.6 Hz，该成分并非齿通基频亦或其倍频，且位于刀尖点各向1阶模态固有频率附近。由图4（b）可知，当轴向切深增加至5.89 mm时，工件表面开始出现振纹，表明此时开始出现切削颤振现象。值得说明的是，随着刀具持续进给，当工件沿进给方向的剩余长度小于10 mm（即刀具半径）时，径向切削宽度ae开始减小，改变了切削系统原有的动力学特性，切削转变为稳定切削，故振纹亦随之消失，如图4（b）中的颤振消除区，此时轴向切深为7.32 mm。综合以上分析可知，当n=3 000 r/min时，机床实际轴向极限切深和颤振频率的标定结果分别为5.89 mm和1 179 Hz。

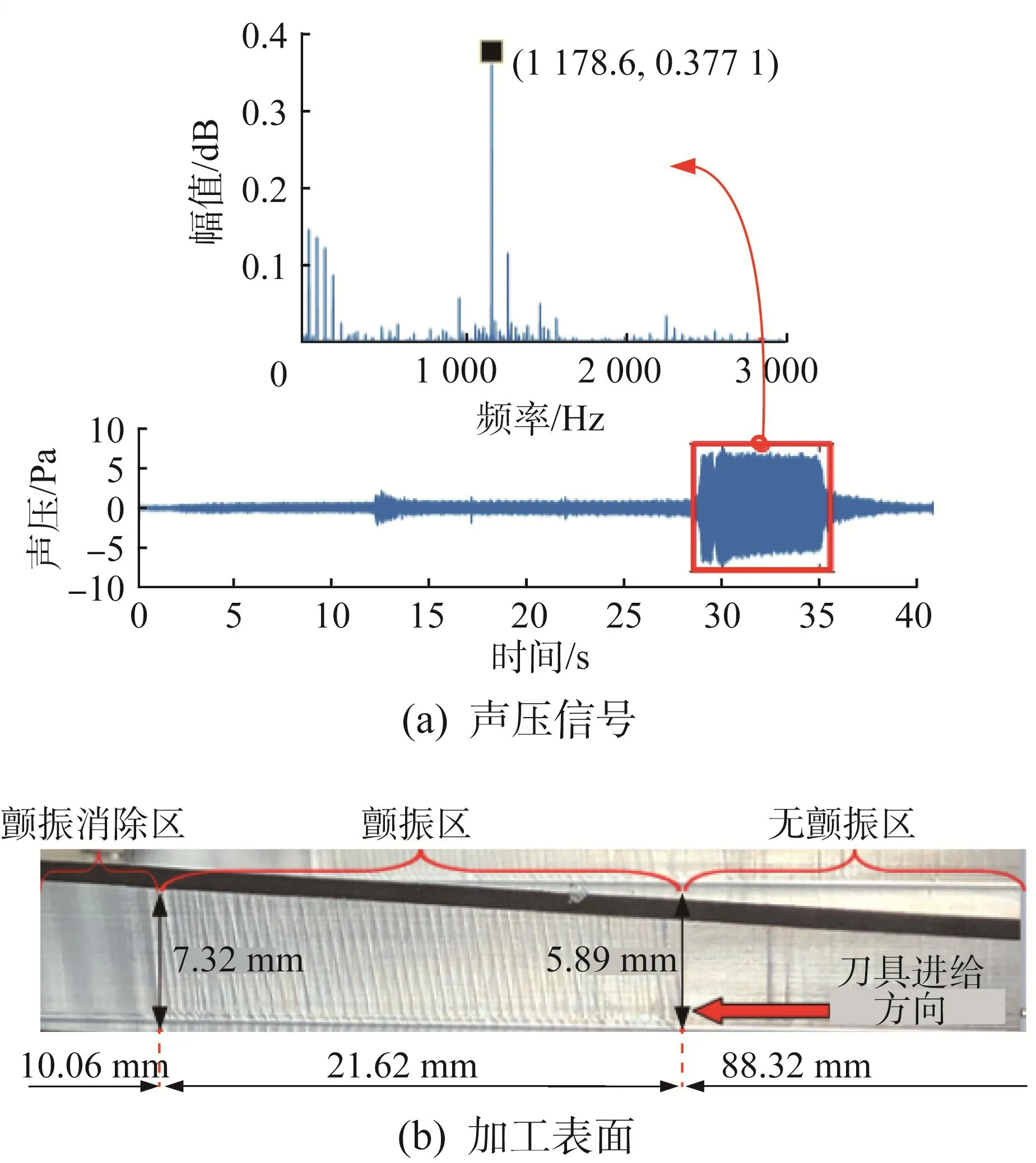
图4 n=3 000 r/min时变切深切削实验结果Fig.4 Experimental results of variable cutting depth milling when n=3 000 r/min

类似地，当n=3 300，4 000 r/min时对噪声信号和加工表面进行分析，可得各转速下切削稳定性标定值，如表2所示。

表2 各转速下切削稳定性标定值Table 2 Calibration value of cutting stability at each rotational speed

2.1.3 刀尖点动力学行为分异特征辨识

根据1.2节所提出的方法，辨识得到不同转速下刀尖点各向模态参数，如表3所示。

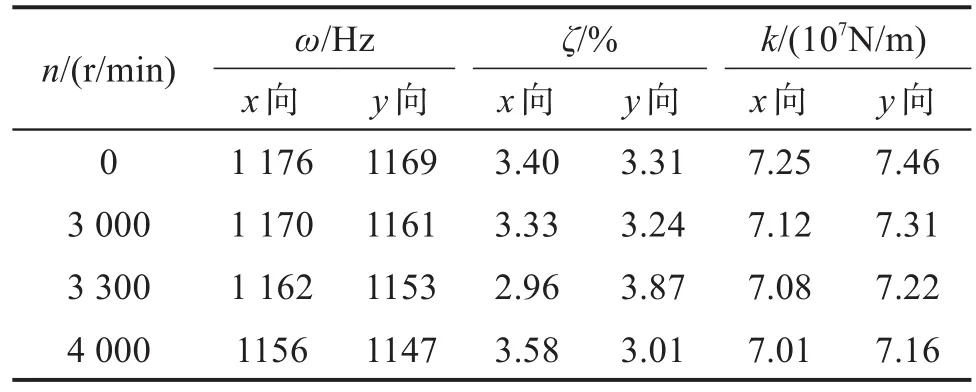
表3 辨识得到的不同转速下刀尖点模态参数Table 3 Tool tip modal parameters identified at different rotational speeds

刀尖点各向模态参数随转速的分异规律如图5所示。由图5（a）和图5（b）可知，刀尖点各向模态固有频率和模态刚度均随转速增大而减小，且转速越大，分异特征越显著；由图5（c）可知，刀尖点各向模态阻尼比随转速增大而产生分异，但未呈明显的分异规律。

图5 刀尖点各向模态参数随转速的分异规律Fig.5 Variation law of tool tip modal parameters with rotating speed

2.2 结果讨论与验证

利用表3所示辨识得到的刀尖点分异动力学参数，进行切削稳定性预测，可得到不同转速下的极限切深，进而得到考虑和未考虑分异特征时机床的实际极限切深与预测极限切深的相对误差，如表4所示。

根据表4所示机床实际极限切深与预测极限切深的相对误差不难看出，未考虑分异特征的刀尖点的动力学特性参数并不适用于切削稳定性的精准预测。以n=4 000 r/min为例，极限切深的实验标定值为6.00 mm，基于静态刀尖点动力学特性参数所预测的极限切深达到了7.76 mm，相对误差为29.2%，而利用该转速下的分异动力学参数预测得到的极限切深为5.98 mm，与标定值的相对误差仅为0.26%。说明所提出的辨识方法能较准确地获取运行状态下刀尖点动力学行为分异特征，并最终实现切削稳定性的精准预测。

此外，分析表4可以发现，运行状态下刀尖点刚度的分异是不可忽略的［21］。因此，对刚度的辨识非常有必要。刀尖刚度对极限切深的影响如图6所示。当n=3 000 r/min时，借助该转速下的刀尖点动力学参数，在考虑刚度分异的前提下，预测极限切深为6.16 mm，实验标定值为5.89 mm，相对误差为4.5%。未考虑刚度分异时的预测值为6.287 mm，相对误差为6.8%，可见预测精度得到明显提升，说明了在辨识过程中进行刚度辨识的必要性。

图6 刀尖刚度对极限切深的影响Fig.6 Influence of tool tip stiffness on limit cutting depth

表4 机床实际极限切深及其与预测极限切深的相对误差Table 4 Actual limit cutting depth of machine tool and its relative error with predicted limit cutting depth

3 结论

1）提出了在主轴运行状态下刀尖点动力学行为分异特征的辨识方法。利用该方法能够准确获取在主轴运行状态下刀尖点的动力学特性及其分异规律，实现切削稳定性的精准预测。

2）利用所提出的辨识方法对所得到的各转速下刀尖点动力学参数进行对比分析，结果表明，刀尖点各向模态固有频率和模态刚度均随转速的增大而减小，刀尖点各向模态阻尼比随转速变化而产生分异，但未呈明显的分异规律。

3）通过对比分析考虑及未考虑刚度分异时切削稳定性的预测精度，结果表明，考虑刚度分异时切削稳定性的预测精度相比于未考虑刚度分异时的预测精度有明显提升，说明了在辨识过程中考虑刚度分异的必要性。