电池储能提高电力系统调频性能分析

2022-01-11王凯丰谢丽蓉鲁宗相

电力系统自动化 2022年1期

王凯丰，谢丽蓉，乔颖，鲁宗相，杨欢

（1. 可再生能源发电与并网技术教育部工程研究中心（新疆大学），新疆维吾尔自治区乌鲁木齐市 830047；2. 电力系统及大型发电设备控制和仿真国家重点实验室，清华大学，北京市 100084）

0 引言

随着可再生能源的发展，预计2050 年中国可再生能源发电占比将达到50%左右，在此能源清洁化进程中，传统机组的发展将达到顶峰并逐渐出现存量替代［1-3］。高比例可再生能源并网给系统频率安全带来了巨大挑战，众多频率安全事故表明，在未来电力系统中为了保证频率安全，需要一种快速的调频资源［4-6］。为符合能源清洁化趋势，以维持火电机组在线比例来保证频率稳定的方法不可取［7］。因此，需要该调频资源能够替代火电机组减少带来的惯性支撑与/或一次调频能力。国内外安全事故快速支援事件从理论和实践上证明了电池储能满足调频资源的种种需求［8］。

与传统机组相比，储能的替代优势有两点:一是储能响应快速性，其响应速度等级为毫秒级［9-10］；二是具备很强的定制能力，可通过电力电子接口控制策略及其参数优化实现与同步机组外特性相近的调频能力［11-12］。储能作为一种新型灵活性调频资源，在调频替代能力方面存在新的问题。在紧急频率调整过程中，储能对于火电机组而言具备何种优势，以及储能作为可定制调频资源，通过参数定制能否最大化体现储能的替代能力，均是当前面临的新问题。

电力系统的常用调频指标为频率变化率（rate of change of frequency，ROCOF）、频率最低点和静态频率偏差等［13-15］。文献［16］探讨了在不同储能容量情况下储能对一次调频效果的改善能力，而文献［17］则从调频辅助服务市场层面对不同储容比情况下调频效果进行了对比分析。文献［18-19］从储能调频有效性层面对其调频效果进行分析，结果表明储能调频的有效性较好。以上文献对储能与火电机组的调频效果进行了分析对比，但未从理论推导和指标方面阐述储能在调频方面的优势及可推广的定量评估指标。

此外，相关研究表明，储能的调频能力要优于常规机组，但未给出定量的数据进行证明［20］。文献［21］基于美国调频市场案例指出，电池储能系统对火电机组的替代效果为火电机组和水电机组中最高。文献［22-23］对火电机组和储能的调频效果进行了对比分析，结果表明储能对火电机组的替代能力约6～25 倍。文献［24］分析了储能对火电机组的替代能力，结果表明储能对火电机组的替代能力为12.5～25 倍。文献［25］分析了储能和火电机组短时间尺度内频率变化，结果表明功率为10 MW、容量为3.66 MW·h 的电池储能系统至少可以代替36 MW 火电机组的调频能力。

以上文献研究表明，目前对储能在电力系统调频中的优势研究大都利用仿真和统计论述储能对调频效果的改善，但未从理论上确定储能具体优势并进行量化。同时，储能调频动态特性不同于火电机组，现有研究大都无法准确表征其对最大频率偏差等参数的贡献。

本文针对以上问题，分析了储能与火电机组参与电力系统调频的原理，从频率调整效果评价指标出发，分析了储能在高比例可再生能源系统中调差系数对调频效果的影响；从功率、能量及频率最低点的贡献出发，提出了评价储能替代火电机组能力的相应指标。最后，构建同功率储能和火电机组调频系统，利用指标对仿真结果进行分析，验证了储能对火电机组的高替代能力。

1 储能调频原理及其优势

1.1 储能虚拟调频模型

电池储能参与电力系统频率调整的方式为通过变流器控制技术来使得储能模拟（或部分模拟）同步发电机的响应特性进行提供频率支援。储能控制分为2 个部分，分别为DC/AC 并网变流器控制和电池系统运行状态控制。

1）DC/AC 并网变流器控制

DC/AC 变流器的控制分为内环控制和外环控制，内环控制主要是内环电流的解耦控制。与内环控制不同，外环控制策略可以灵活定制，其控制策略可以实现固定增量控制、变化增量控制、下垂控制和综合惯性控制，如附录A 图A1 所示。

储能响应频率偏差的控制方法中使用较为广泛的为有功功率-频率下垂控制策略，如附录A 图A1（c）所示。其调频过程中有功功率增量如式（1）所示［26］。

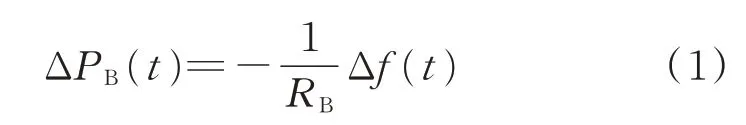
式中:ΔPB(t)为t时刻储能有功功率增量；RB为储能调差系数；Δf(t)为t时刻系统频率偏差。

2）电池系统运行状态控制

储能参与电力系统频率调整时可以自主设定其参数，同时储能参与调频时其调节范围理论上为全功率范围调节。附录A 图A2 为储能和传统机组调差系数设置范围及出力调节范围对比示意图［4，7，18，24］，图中红点表示此刻调频资源出力状态，蓝线表示调频时各调频资源的出力变化范围。其中传统机组受到自身物理特性的约束，调节范围较小，仅能增加或减小输出功率的大小；而储能可以在全功率Pmax范围内变化，既可以充电，也可以放电。

从图A2 可以看出，与火电机组不同，储能的理论调节范围为[-Pmax，Pmax]。由式（1）可得:

式中:Pmax为储能最大充放功率。

考虑到储能寿命等因素，储能参与调频时其功率输出也受到荷电状态（state of charge，SOC）的约束。系统频率波动较小时，储能在SOC 区间为[Slow，Shigh]（一般设为40%～60%）的情况下进行浅度充放更有利于延长储能的使用寿命；但频率波动较大时，为保障系统稳定，允许储能进行深度充放，此时SOC 约束区间为[Smin，Smax]（一般设为10%～90%）。当SOC 越限时，即储能充满或放空时，储能系统停止工作。其中，储能注入或吸收的功率由系统频率偏差和ROCOF 决定。其控制策略如附录A图A3 所示。

3)储能等效模型

储能整体控制过程由储能运行控制和变流器控制组成，因此其等效模型如式（3）和式（4）所示。

1.2 储能调频优势

储能系统的物理特性决定了其响应速度较快，这可以令储能先于火电机组参与频率调整，调频中等效模型阶数较低，在稳定性方面优于火电机组，在参数RB定制情况下不会出现系统振荡或失稳的情况。

1）改善频率响应动态

为了明确储能在调频过程中的优势并分析储能快速响应能力特点，利用稳定判断方法对储能和火电机组的参数特性进行分析。

火电机组和储能参与电力系统频率调整的传递函数如式（5）和式（7）所示，其推导过程见附录B。

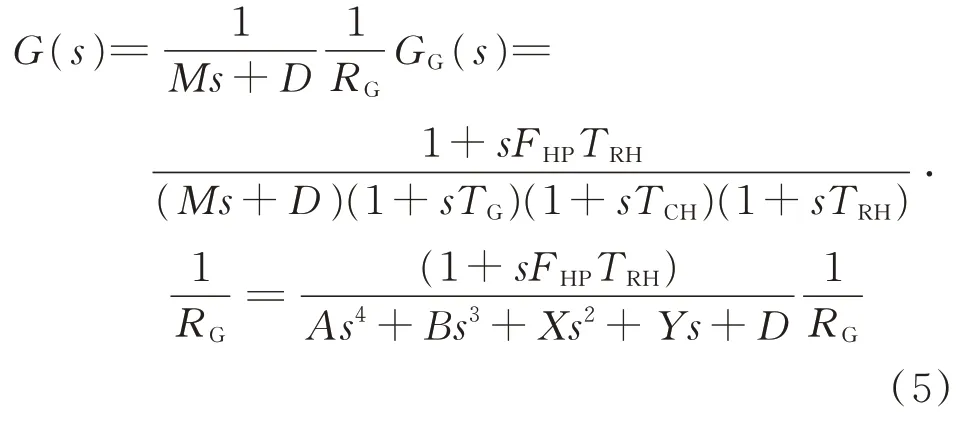
其中

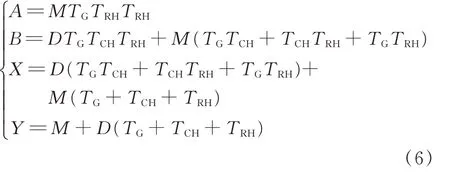
式中:M=2H，其中H为系统惯性时间常数；D为系统阻尼系数；GG(s)为火电机组的传递函数；TG为火电机组响应时间常数；RG为火电机组的调差系数；TCH为汽轮机时间常数；TRH为再热器时间常数；FHP为再热器增益。

以储能和火电机组的调差系数为变量，利用根轨迹法分析储能和火电机组调差系数变化对频率调整稳定性的影响，其中1/RG的取值范围为0～25，1/RB的取值范围为0～100，分析结果如图1 所示。

图1 储能和火电机组关于调差系数的根轨迹对比Fig.1 Comparison of root locus of differential coefficient between energy storage and thermal power units

采用储能调频时，系统过阻尼，而含汽轮机和再热器的火电机组调频系统为欠阻尼系统。图1 表明，随着储能调差系数降低（如紫色实线所示），其离虚轴最近的特征根将越来越远离虚轴，此时系统的调频稳定性会越来越强；而火电机组调差系数的降低则会使其离虚轴最近的特征根越来越靠近虚轴（如蓝色实线所示），同时，较高的调差系数易导致系统发生振荡。

2）快速响应能力

设定2 个系统负荷和调频资源装机容量均相同，其中一个系统仅利用储能参与调频，另一个系统仅利用火电机组参与调频，系统参数设定如附录C表C1 所示。设阶跃扰动为0.05 p.u.，分析在同扰动下储能和火电机组的响应能力，储能和火电机组的出力对比如附录A 图A4 所示。

由图A4 可知，储能的响应速度远快于火电机组，储能达到稳定出力的时间约为1 s，而火电机组达到稳定出力的时间约为6 s。同时储能系统响应信号时的曲线未出现超调，而火电机组的响应曲线出现了超调，这表明储能响应频率变化的能力大于火电机组。当频率刚发生变化时，储能可对电力系统频率变化进行快速响应，以较高的爬坡率为系统提供大量快速有功功率支撑。而火电机组由于受到其爬坡率影响，其响应电力系统频率变化的能力弱于储能。经过几秒后，储能和火电机组均达到恒定出力，因此评价储能调频与火电机组的调频优势对比一般在频率发生变化时的前数秒。

储能的快速响应能力使得电力系统频率变化初期获得大量有功功率支撑，减缓了频率降低的速度，降低了系统的ROCOF，减小了系统最大频率偏差Δfnadir，保障了系统的频率稳定性。

3）储能调频能力对比指标

设定在同一系统中，新增储能和火电机组在同一负荷扰动下向系统输入有功功率参与调频。引入不同类型机组参与电力系统频率调整时的出力状况对储能的调频优势进行评价，如式（8）和式（9）所示。结合附录A 图A4 可以看出，在频率变化初期，储能出力远大于火电机组，此时储能的替代能力较高。而随着系统逐渐恢复平衡，储能出力和火电机组的出力达到一个定值，此时储能对火电机组的替代能力也将趋近于一个定值。

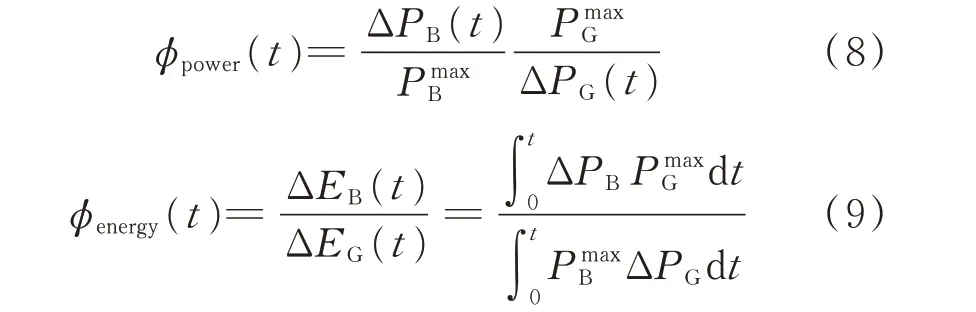
式中:φpower(t)为t时刻调频资源功率替代能力评价指标；φenergy(t)为0～t时间段内调频资源能量替代能力评价指标；ΔPG(t)为火电机组在t时刻向电网注入的功率；PmaxB为新增储能最大输出功率；PmaxG为新增火电最大输出功率；ΔEB(t)为0～t时间段内储能向电网输入的总电量；ΔEG(t)为0～t时间段内火电机组向电网输入的总电量。

2 储能调频对电力系统的影响及量化指标

在电力系统调频中，调频资源（火电、水电和储能等）的调差系数R决定了其响应电力系统频率变化的能力，是衡量调频资源对系统频率影响的重要指标［27］。同时储能的动态特性不同于常规机组，同等R的降低对电力系统频率改善的能力也不相同，因此本文以同频率最低点时储能对常规机组的替代能力ρ作为一项新的指标。

2.1 储能调频对高新能源渗透率系统参数的影响

根据上文推论可得，机组调差系数越小，其调频效果越好。实际工程中，汽轮发电机的调差系数一般取值为4%～5%，水轮发电机的调差系数一般取值为2%～4%，而储能系统可通过自行设定。

同类型的调频资源包含多台机组，参数相同的多台机组运行时可将其等值为一台机组表示，其等值调差系数Rt为:

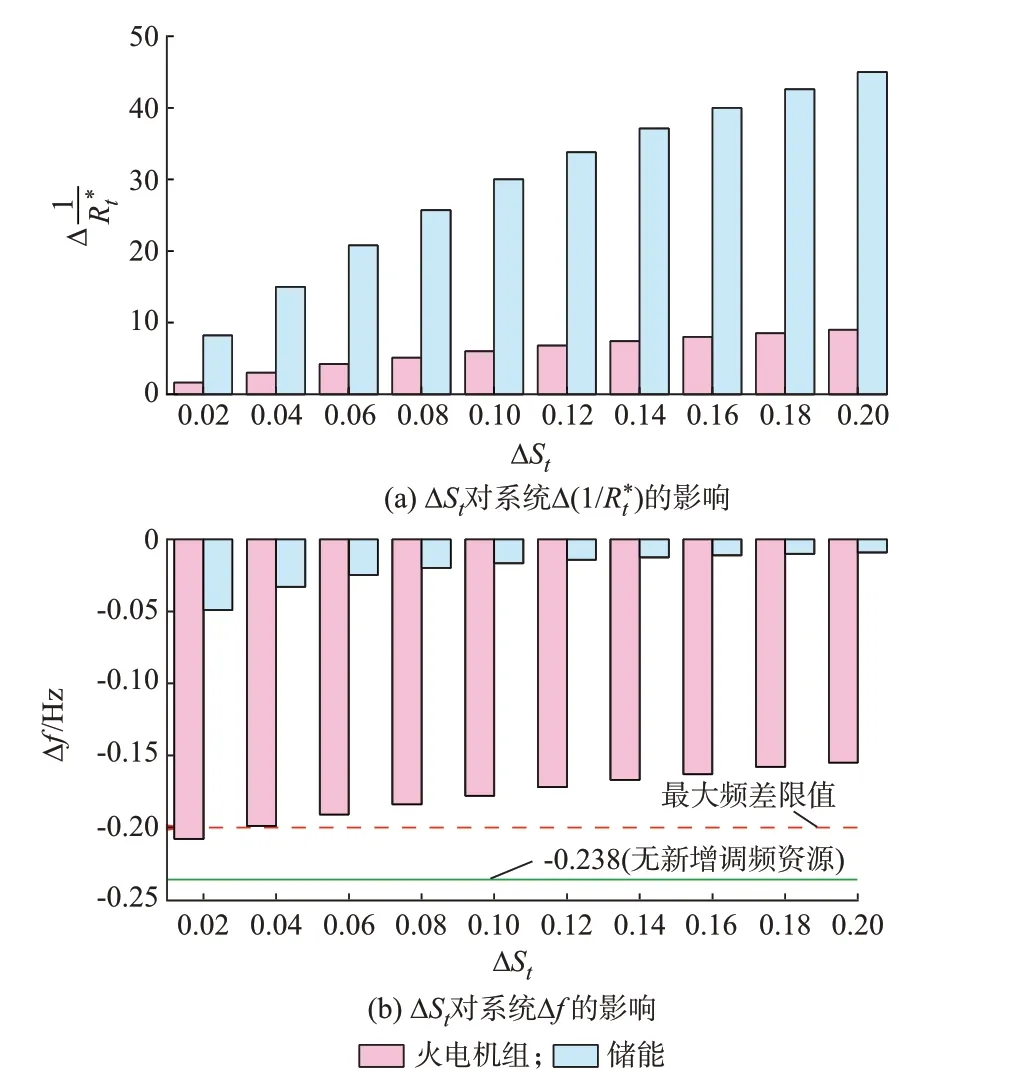
图2 ΔSt 对Δ(1/)和Δf 的影响Fig.2 Influence of ΔSt on Δ(1/) and Δf

2.2 储能提高频率最低点的替代指标

频率最低点Δfnadir是评价电力系统调频能力的一项重要指标，为直观表明储能的替代能力，以储能和火电机组在同一扰动下达到所设定的频率最低点时增加的装机容量作为对比参数，储能容量替代能力计算流程如图3 所示。式（12）以达到相同频率最低点时各调频资源装机容量之比为评价指标来评价不同类型机组的调频能力。

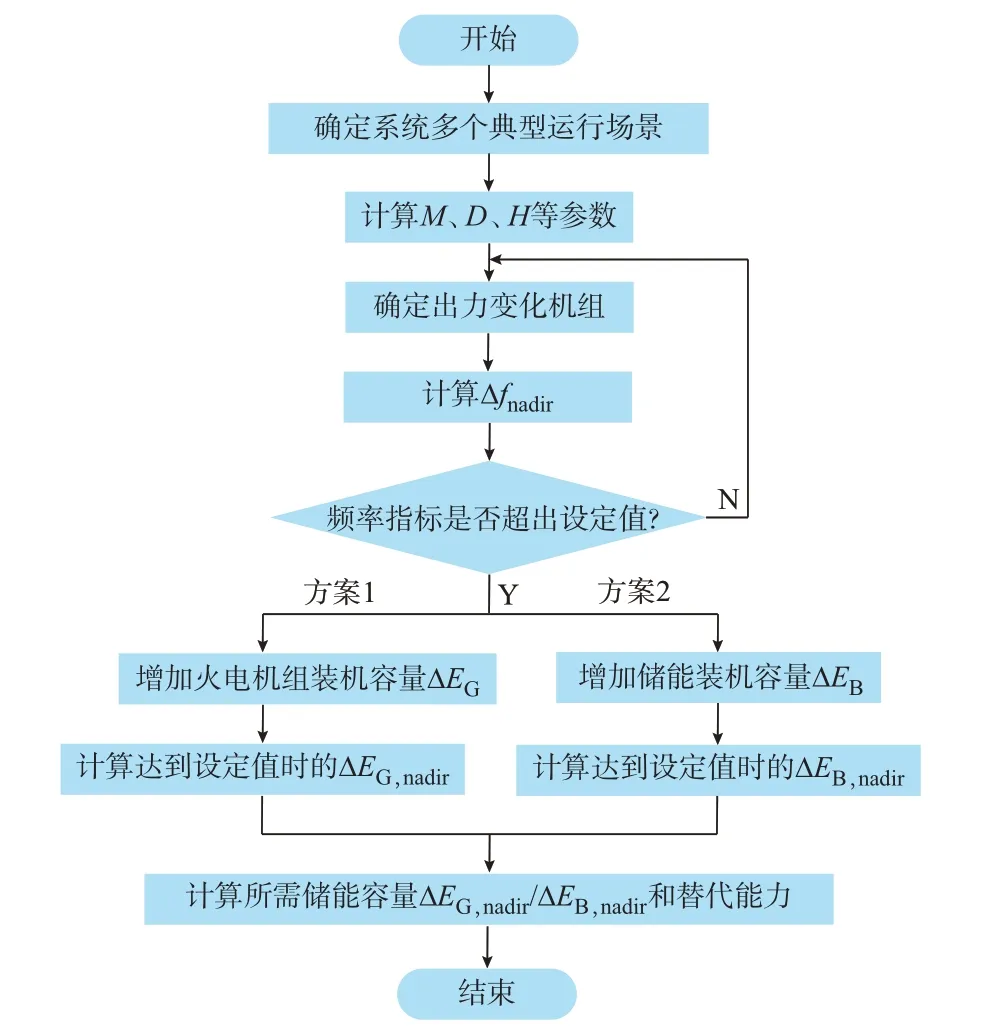
图3 储能容量替代能力计算流程Fig.3 Calculation process of substitution ability of energy storage capacity

式中:ρ为达到同一频率最低点时各类型调频资源新增装机容量之比；ΔEG，nadir为达到频率最低点时新增火电机组装机容量；ΔEB，nadir为达到频率最低点时新增储能装机容量。

如图3 所示，首先设定新能源发电占比从0%逐渐增长到45%，以此设定电力系统中负荷、各机组装机容量和扰动大小等参数，确定多个典型的运行场景。根据各场景所设定的参数计算系统中M、D和H等参数，同时确定在频率变化时系统中能参与调频的机组出力。其次通过系统的频率变化计算系统频率偏差，若最大频差超过所设定的频率稳定边界标准0.2 Hz，则增加储能或火电机组来参与调频。计算增加调频资源后的系统参数变化直至系统满足频率指标，此时停止增加调频资源。最后根据所增加的储能和火电机组的容量计算储能对火电机组的容量替代能力。

3 算例分析

3.1 仿真参数设置

以中国东部某区域电网为例进行案例分析，系统中各电源构成如下:总负荷为138 GW，受电25.7 GW，火电机组发电占比58.48%，水电机组发电占比7.08%，其他不参与调频的机组发电占比12.26%，一次调频限幅6%，火电机组和水电机组延迟为20 个工频周期，储能延迟为1 个工频周期［27］。以额定功率138 GW 和额定频率50 Hz 为基准进行数据标幺化。后期投入0.005 p.u.的同功率火电机组和储能进行辅助调频。其余参数设置如附录C 表C1 所示，其中RG1为原始系统火电机组调差系数，RG2为新增火电机组调差系数，RH为原始系统水电机组调差系数［28-29］。

以阶跃负荷扰动和随机负荷扰动作为输入，对不同机组参数的调频效果进行对比分析，确定储能相比于火电机组在频率调整方面的优势。

3.2 同功率储能和火电替代能力对比

以3.1 节所设系统为例进行同功率储能和火电机组的短时间尺度功率支撑能力对比分析。设负荷值为0.04 p.u.的阶跃扰动，新增调频资源功率为0.005 p.u.，利用式（8）和式（9）对2 种调频资源的出力进行对比，其结果如图4 所示，具体仿真结果见附录A 图A7。

图4 阶跃扰动下的指标值Fig.4 Index values under step disturbance

由图4 可知，储能对火电机组的替代效果在频率变化初期是最高的，且随着时间的推移，其替代效果逐渐降低。由于在频率变化初始阶段储能出力较大而火电机组未响应，导致储能对火电机组的替代能力较大，此时替代能力指标最高可达100 左右。但随着火电机组的逐渐响应，储能和火电机组的出力会逐渐趋于恒定，此时储能对火电机组的功率和能量替代能力会逐渐趋近一个定值。表1 展示了阶跃扰动下不同时间点的功率和能量替代能力。

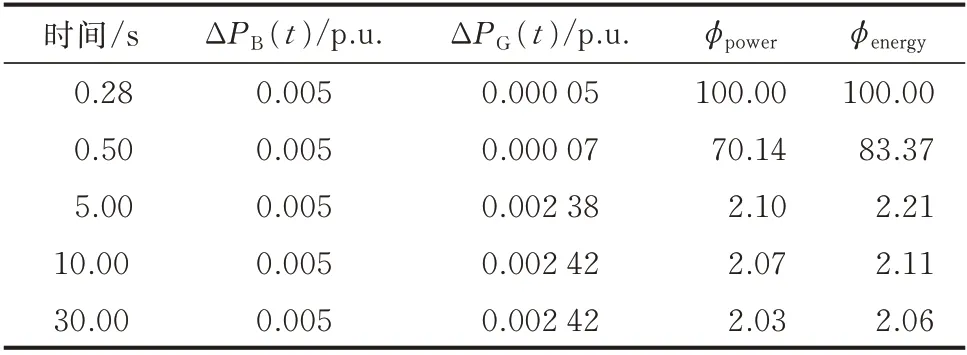
表1 阶跃扰动下的功率和能量替代能力Table 1 Substitution ability of power and energy under step disturbance

由表1 可知，在阶跃扰动下，由于储能的快速响应能力，短时间内的储能对火电机组的功率和能量指标都比较大，0.5 s 时的替代能力为75 左右。而随着储能出力和火电机组出力逐渐趋近相同，其平均功率和能量指标则逐渐降低，最终在30 s 时系统趋于稳定，此时储能的功率和能量替代能力趋近于2。

利用信号叠加，以幅值范围为-0.02 p.u.～0.05 p.u.的连续信号作为扰动，其扰动信号如附录A 图A8 所示，其频率变化如附录A 图A9 所示。对其频率波动进行比较，如附录A 图A10 所示。与原系统调频效果相比，增加储能的频率改善效果提高了16.2%，而增加火电机组的频率改善效果仅提高了0.167%，可以看出同等功率下储能的调频改善效果是火电机组的近百倍。

在随机扰动中，虽然信号随机波动，但随着储能和火电机组的参与，该时刻系统的频率趋于稳定。同时，下一时刻扰动相较于上一时刻的扰动变化较小，储能和火电机组出力之比的变化不大，因此与阶跃扰动类似，随机扰动下储能对火电机组的替代能力在初期较大，但最终的替代能力将趋近于2 左右。

综上所述，储能在频率变化初期所提供的有功功率为火电机组的数倍。但随着火电机组的逐渐响应，二者之间的出力比值逐渐趋向定值。同时储能调差系数的可定制性使得储能能够在短时间内快速达到最大出力。因此可得储能对火电机组的高替代能力主要发生在频率变化初期的短时间内，其主要作用是为电力系统提供短期频率支撑。

3.3 同指标下储能和火电替代容量对比

系统频率稳定指的是系统在受到负荷扰动时，不需要切机切负荷等动作且通过调频机组的调节可以使系统的最大频率偏差不超过频率稳定边界标准并最终恢复稳态。当系统最大频率偏差超出所设定的频率稳定边界标准时，可通过新增储能或火电机组参与调频提高频率稳定，持续增加调频资源直至该系统在受到同样扰动时其最大频率偏差不超出所设定的阈值。此时所增加的火电机组和储能的容量之比即为储能对火电机组的容量替代能力。以3.1节所设系统为例，对在达到同一设定的频率最低点时所增加的火电机组和储能装机容量进行对比分析。设定0.2 Hz 的频率偏差为电力系统频率稳定边界标准，设定扰动为0.05 p.u.，结果如图5 所示。

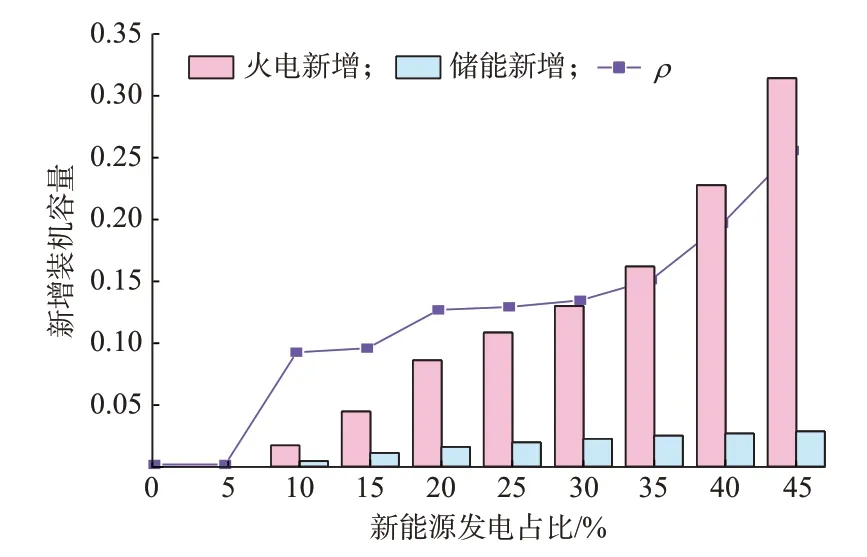
图5 储能容量替代能力Fig.5 Capacity substitution ability of energy storage

从图5 可以看出，当新能源发电占比较小时，此时系统频率仍处于稳定范围内，频率的偏差处于调频死区内，不需要新增储能和火电机组装机容量也足以保证系统的频率稳定性。而随着新能源发电占比增加，储能的调频优势会逐渐凸显，同时对火电机组的容量替代能力则会逐渐增强。当新能源发电占比从10%增长到45%时，储能容量替代能力将会从1 快速上升到14 左右。考虑到高比例可再生能源并网的发展趋势，大量增加火电机组装机容量的情形很难发生，储能将成为电网中最有价值的调频资源。