基于深度强化学习的居民实时自治最优能量管理策略

叶宇剑，王卉宇，汤 奕，Goran STRBAC

（1. 东南大学电气工程学院，江苏省南京市 210096；2. 伦敦帝国理工学院电气与电子工程系，伦敦SW72AZ，英国）

0 引言

随着分布式光伏、电动汽车（electrical vehicle，EV）等柔性负荷及储能（energy storage，ES）等分布式资源（distributed energy resource，DER）在居民智能用电中的普及［1］，居民的能量管理面临着由各类不确定性因素带来的挑战。与此同时，智能电表和通信等技术的快速发展为监测和控制居民DER 设备提供了关键的技术支撑［2］，大数据和人工智能技术的发展则为能量管理优化提供了数据驱动的新途径［3］。

家庭能量管理系统（home energy management system，HEMS）作为能量管理技术在用户侧的体现，可有效管理用户电能生产、使用及存储过程［4］。现有大部分文献采用基于模型的最优化方法作为技术路线。其中，文献［5-7］采用确定性优化模型，构建各类DER 的运行模型，依靠对负荷、光伏功率等的预测，以最小化日用电成本为目标优化能量管理决策。然而，用户侧DER 运行模型受到外部环境、用户行为等因素的影响呈现出动态变化，不确定性较强且模型构建精度较低［8］。此外，用户侧负荷和光伏的强随机性与间歇性使得预测误差高于大电网的同类预测问题［1］，影响确定性优化的性能。

为应对不确定性，文献［9］采用基于场景的随机规划方法，假设各不确定性参数所对应的概率分布模型，通过蒙特卡洛模拟产生对应的场景，但因受到外部因素的影响，所假设的概率分布往往与实际分布偏差较大。另外，问题求解规模会随着不确定性场景数目的增加而急剧扩大。文献［10］采用鲁棒优化模型以集合的方式来描述不确定性，以集合内最劣场景下的最小成本为目标，最大限度地抑制不确定性对决策造成的干扰，但存在对集合构建合理性的高依赖性和策略的保守性［11］。文献［12-13］采用模型预测控制（model prediction control，MPC）以滚动优化的形式提升了鲁棒性，但是计算负担较大，且优化性能直接受到预测误差的影响。

上述基于模型的能量管理优化方法的性能依赖于对各类DER 设备运行模型构建的精度，而追求精细化建模易使得优化问题具有非凸和非光滑特性，增大了求解难度与计算负担，使得所得策略多适用于线下的应用，难以实现实时能量管理优化的目标［8］。强化学习（reinforcement learning，RL）作为一种数据驱动的人工智能技术，在智能体与环境交互过程中学习策略达成回报最大化，不依赖于对被控对象的先验知识［14］。针对实时能量管理优化问题，RL 提供一种自趋优式的策略学习方法，不依赖于对未来信息的准确预测，仅基于当前对系统状态的感知进行策略优化。 深度强化学习（deep reinforcement learning，DRL）兼具深度神经网络的普适函数逼近能力和强化学习的决策能力，在电力系统决策领域得到了广泛应用［15］。文献［16-17］采用深度Q 网络算法进行家庭综合需求响应的在线优化，但该算法不适用于高维连续动作空间，若将空间离散化易产生维数灾［18］。文献［19］采用深度策略梯度算法学习柔性负荷的启停策略，而负荷功率则通过求解优化问题获得，本质上未实现无模型的负荷控制。另外，该算法因缺少策略评估环节，面临着梯度估计方差高导致的收敛速度较慢与策略次优等问题。基于深度确定性策略梯度算法，文献［20］提出了面向用户侧多能源系统的优化调控方法。该算法的优化性能依赖于诸多超参数的调节［18］，无法同时学习离散与连续的能量管理策略。

本文提出了基于近端策略优化（proximal policy optimization，PPO）算法的无模型能量管理优化方法。首先，对用户DER 设备按运行特性进行分类，并用统一的三元组信息描述各类设备的运行状态，确定相应的能量管理动作，将实时能量管理优化问题描述成序贯决策问题。其次，以智能电表所采集的多源时序数据作为原始输入，提出基于长短期记忆（long short-term memory，LSTM）神经网络的时序特征提取技术，进而辅助DRL 进行序贯决策，在最小化用电成本的同时提升能量管理策略的鲁棒性。另外，本文提出基于深度神经网络的连续-离散混合策略函数，赋能在多维连续-离散混合的动作空间中高效学习最优的能量管理决策。最后，仿真验证了所提方法的有效性。

1 HEMS 建模

1.1 居民DER 设备分类及建模

本文给出了HEMS 的整体框架和各类常见家用设备。如图1 所示，居民DER 设备一般包含分布式光伏、ES、不可转移负荷和可转移负荷，而可转移负荷可再分为可中断与不可中断负荷［21-22］。

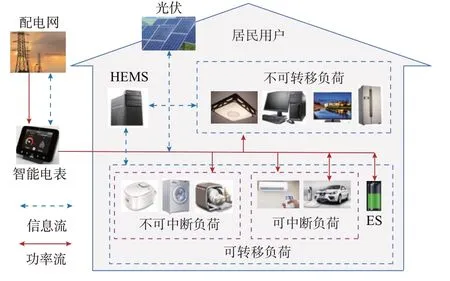
图1 HEMS 结构示意图Fig.1 Schematic diagram of structure of HEMS

对于任意设备n∈{1，2，…，N}，其中N为设备总数，其t时刻运行状态sn，t可用以下三元组进行描述:

式中:ωn，t∈{0，1}表示设备n在t时刻的运行状态，其值为1 表示设备n在t时刻处于可运行时段，为0则表示设备n在t时刻不可运行；ρn，t∈[0，1]表示设备n在t时刻的任务完成进度；πn，t描述设备n在t时刻的特有属性。

1.2 可中断负荷

可中断负荷的用电功率具有连续可调性，本文主要考虑2 类典型可中断负荷:暖通空调（heating，ventilation and air conditioning，HVAC）和EV。因ES 的运行特性与EV 相似，故一同考虑。

1.2.1 HVAC

HVAC 具有制冷与制热2 种模式，温度设定值与运行时段可根据用户的需求灵活设定以保证用户的舒适度。HVAC 的功率取决于温度设定值、室内与室外温度、热阻抗等因素，可在保证用户舒适度的情况下综合上述因素进行功率调节［23］。HVAC 在t时刻的状态根据三元组的定义可表示为:

式中:Toutt为t时刻的室外温度；ηAC为热转化效率，其值为正代表制冷、为负代表制热；Δt为每个控制时段的长度；RAC和CAC分别为热阻抗和热容量。

1.2.2 EV 与ES

EV 因具备与电网之间的能量交互V2G（vehicle-to-grid）和与住宅之间的能量交互V2H（vehicle-to-home），是重要的能量存储设备且具有较高的可调度性［24］。EV 运行状态的定义需满足功率与能量的相关约束，并且作为一种交通设备，其接入与断开电网的时间与用户行为有关，具有随机性。EV 在t时刻的状态根据三元组的定义可表示为:

基于式（7），EV 电池t+1 时刻的SOC 可表示为［25］:

ES 与EV 的关键区别在于ES 的可充放电时段为全天，其余特性与EV 相似，因此，运行状态可按照上述方式类似描述。

1.3 不可中断负荷

式中:SA 的可运行时段为(tSAα，tSAβ)，故SA 的运行状态ωSAt在该时段内设定为1，在其余时段设定为0；ρSAt表示任务当前的完成进度，即已完成用电步骤占总步骤数目的比值；πSAt表示完成可运行时段的剩余时间。

式（10）中，第1 个等式保证了SA 可连续按顺序完成K个运行步骤；第2 个等式确保SA 在截止时间前完成整个运行周期；第3 个等式表示除SA 可运行时段外，其余运行周期无法被执行。

图2 智能家电的运行状态定义Fig.2 Definition of operation status of SAs

式中:t′=K。

1.4 实时能量管理优化的马尔可夫决策过程建模

家庭用电设备的实时能量管理优化问题可建模成一个马尔可夫决策过程（Markov decision process，MDP），并采用无模型RL 的方法进行策略优化。MDP 通常由以下主要元素进行描述。

1）智能体与环境:HEMS 作为本文中的智能体，与环境交互学习经验并对能量管理策略进行优化。环境为1.2 节和1.3 节中描述的所有DER 设备构成的用电系统。

2）状态集（S）:t时刻环境状态st可定义为

4）奖励函数（R）:能量管理的优化目标是在保证用户舒适度和满足各设备运行约束下的用能费用最小。因此，奖励函数rt的设置包含以下3 个部分。

（1）用能费用:

（3）惩罚项:针对EV 用户而言，出行前需保证电池能量足够出行，对于违反该运行约束的部分可通过惩罚项施加在奖励函数上，该项表示为式（17）。

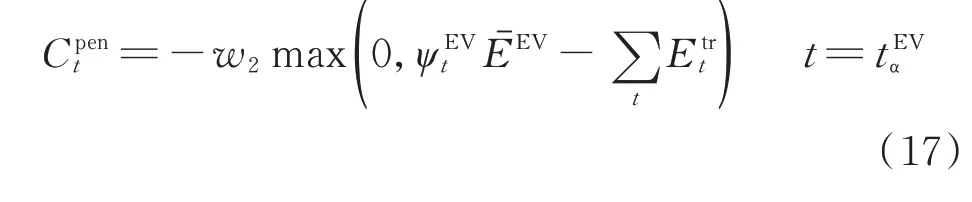
具体的MDP 表现为在每个控制时段，智能体（即HEMS）根据当前观测到的环境状态st，按照当前策略执行对各设备的能量管理动作at，环境在at的执行后转换至新的状态st+1，智能体得到奖励，接着通过RL 更新策略，从而达到实时感知环境状态来进行自趋优式策略学习的效果。智能体学习的目标在于求解最优策略使T个运行时段的总期望折扣奖励J(π)最大，目标函数可表示为

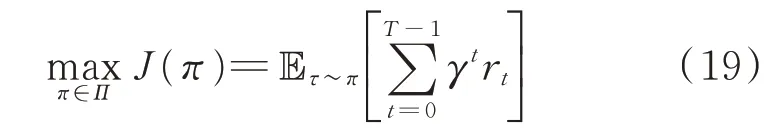
式中:E 为数学期望；τ=(s0，a0，r0，s1，…)为智能体与环境不断交互所产生的状态、动作和奖励序列；π表示智能体所采用的策略，反映环境状态到选择动作概率的映射关系；Π为策略集；γ∈[0，1]为折扣因子，以平衡短期与长期回报；T为控制时段总数。

2 基于LSTM 网络的时序数据特征提取

用电DER 设备的运行特性各异造成HEMS 感知信息的多元化，形成了复杂的高维度状态空间。智能体观测的环境状态可分为:1）直接受动作影响的内部状态特征，即用三元组描述的所有用电设备的运行状态；2）不受动作影响的外部状态特征，包含具有高度不确定性的电价、负荷、光伏发电和室外温度等时序数据，这些都对智能体的序贯决策优化有着较大影响。

针对上述问题，本文采用深度学习方法，不依赖于对上述不确定性因素进行概率建模，采用基于LSTM 神经网络［27］将上述多源时序数据作为原始输入，提取其在长时间尺度上的相似关联特征以更好地描述当前环境下的状态，以辅助DRL 进行策略优化，方法结构如图3 所示。

图3 基于LSTM 和深度神经网络的时序特征提取及策略拟合示意图Fig.3 Schematic diagram of sequential feature extraction and strategy fitting based on LSTM and deep neural network

LSTM 是一种非线性循环神经网络（recurrent neural network，RNN），因其兼顾数据的时序性与非线性，被广泛用于电力系统负荷［28］及电价［29］预测等领域，突出特点在于可充分反映输入的长时间序列数据的长期历史过程［27］，赋能对当前环境状态更好的感知，进而辅助DRL 基于感知信息进行策略优化。

在本文家庭能量管理优化问题中，由于电价、室外温度、负荷与光伏功率等不确定性因素在长时间尺度上具有强相关性，故采用LSTM 进行关于后者的提取。如图3 所示，LSTM 网络包含1 个输入层、1 个输出层以及J个隐藏层。LSTM 网络输入层包含式（12）中t-M+1 到t时刻之间M个时段的外部状态特征数据。LSTM 网络具备输入门、遗忘门和输出门间的门控机制［27］，最后一层在t时刻输出所提取外部状态特征的未来走势，与内部状态特征合并后作为基于深度神经网络的策略函数的输入。

LSTM 神经网络可实现对原始多源时序数据未来走势的良好感知，以此提升能量管理策略应对不确定性因素的能力。

本文提出基于深度神经网络的连续-离散混合策略函数，不仅可以实现对SA 用电步骤执行与否的离散动作，还能够实现对HVAC、EV 和ES 的功率调节的连续动作，克服了现有RL 算法通常只能输出纯离散或连续动作的弊端。式（20）为连续-离散混合策略函数，其中离散动作服从伯努利分布B(p)，连续动作则服从高斯分布N(μ，σ2)。

式中:π(at|st)表示根据当前观测到的环境状态st，按照当前策略π执行对各设备的能量管理动作at；p为是否执行SA 用电步骤的概率，即p(st|=1)，其中表示t时刻第n个SA 是否执行当前运行步骤；μ和σ2分别为对应HVAC、EV 和ES 功率调节动作的均值与标准差。

如图3 所示，基于深度神经网络的策略（红色虚线框）的输入为t时刻所提取外部状态特征的未来走势以及t时刻智能体观测到的内部状态特征，包括设备运行状态、运行进度和运行属性，输出为概率分布所对应的参数p、μ、σ2。最后，随机策略依据所生成的概率分布取样选择t时刻的离散与连续动作，赋能智能体同时学习离散与连续动作，实现对各设备的良好控制。

3 PPO 算法原理及应用流程

3.1 PPO 算法原理

基于上述对家庭能量管理优化MDP 的介绍，以及对MDP 过程中各元素的定义，进一步优化智能体采用的策略函数。通过DRL 的更新策略，目标为求解最优策略使得在保证用户舒适度和满足各设备运行约束下的日用能成本最小。

早期基于梯度的RL 算法采用数值或抽样方法计算梯度，但难以确定合适的迭代学习率。因此，文献［30］提出了处理随机策略的置信域策略优化（trust region policy optimization，TRPO）算法，算法中引入了可衡量新策略与旧策略差异程度的KL 散度（Kullback-Leibler divergence）定义置信域约束，通过选取合适的步长使得策略更新后的奖励值单调不减。为降低TRPO 算法中二阶Hessian 矩阵计算的复杂程度，提高计算效率，文献［31］进一步提出了基于一阶导数策略优化的PPO 算法。

作为基于策略梯度的DRL 算法，PPO 算法具有收敛稳定、性能好的特性。此外，PPO 算法采用执行器-评判器（Actor-Critic，AC）架构，图4 描述了执行器与评判器神经网络的更新流程。PPO 算法训练时，从经验回放库中抽取一个小批量经验样本供网络参数更新。评判器网络通过时序差分误差ς的学习方法更新网络参数φ，计算公式如下:

图4 PPO 算法的离线训练流程示意图Fig.4 Schematic diagram of off-line training process of PPO algorithm

式中:Vφ(st)为状态值函数。

执行器网络则通过优化改进TRPO 算法的目标函数更新网络参数θ。PPO 算法不仅解决了一般策略梯度方法数据样本利用率低和鲁棒性差的问题，还通过式（22）至式（28）对TRPO 算法的目标函数进行转换以提高学习效率。

TRPO 算法的最终目标函数为:

约束为:

式中:πθi+1和πθi分别代表新策略与旧策略；ρπθi为基于旧策略的状态访问概率；Aπθi(s，a)为优势函数，用来表征策略πθi下动作at相对平均动作的优势；DKL(πθi//πθi+1)为新策略和旧策略之间的KL 散度；δ为置信域，用以限制KL 散度的范围。

对式（22）中的目标函数进行一阶近似并采用蒙特卡洛方法近似期望后为:

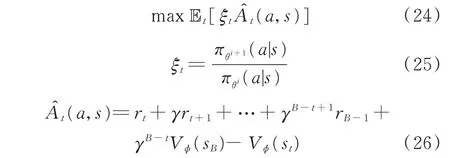
此外，PPO 算法为进一步简化计算过程，对式（24）进行了裁剪，进而得到新的目标函数Lclip。Lclip为算法规定了2 个约束，从而使新旧策略比率ξt约束到[1-ε，1+ε]之间，其中ε为裁剪率，确保能起到TRPO 算法中置信域δ的作用，即

其中

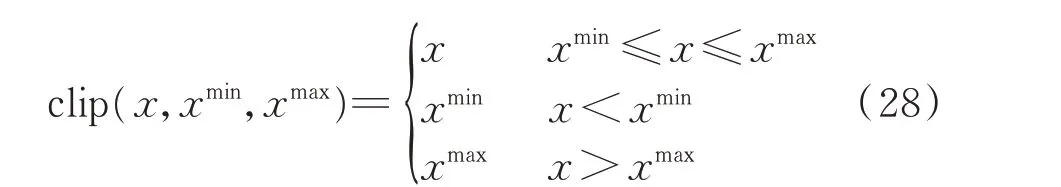
因此，Lclip实现了一种与随机梯度下降兼容的置信域修正方法，并通过消除KL 损失来简化算法及降低适应性修正的需求。

3.2 应用流程

PPO 算法具体在本文的能量管理问题的应用流程分为离线训练和在线部署。

1）离线训练:图4 所示为PPO 算法离线训练流程的示意图。首先，分别初始化执行器和评判器网络参数θ和φ，在训练集中随机选择一天获取其初始状态s1。在每个控制时段t，智能体基于当前状态st（式（12））和策略πθi(a|s)，选择动作at（式（13））改变环境状态并获得奖励rt（式（18）），将经验(st，at，st+1，rt+1)存储到经验回放池。接着，通过随机小批量抽取L个经验样本(sl，al，sl+1，rl+1)，l=1，2，…，L，将(sl，al)输入执行器网络，根据式（25）计算新旧策略比率ξl。

训练评判器网络时，以小批量样本中(sl，sl+1)为输入，依据式（21）计算时序差分误差ς，更新网络参数φ，并根据式（26）计算优势函数A^l(a，s)。最后，由式（27）、式（28）对其进行裁剪得到最终的目标函数Lclip，并更新网络参数θ以得到新策略πθi+1(a|s)。在下一个控制时段，上述过程被重复，直至完成共T个时段的序贯决策过程。

2）在线部署:智能体在线部署后的决策仅依靠已完成训练的执行器网络，而无需评判器网络。首先，载入执行器网络训练后的最优参数θ*，获取任一测试日初始状态s1，在该测试日每个控制时段t，根据策略πθ*(at|st)执行动作at，与环境交互得到奖励值rt和新状态st+1，直至完成共T个时段的决策过程。

4 算例分析

4.1 算例设置

本文算例依据澳大利亚配电公司Ausgrid 所提供的真实数据作为场景，以验证所提PPO 算法的有效性。数据库中包含2011 年7 月1 日至2012 年6 月30 日期间以30 min 为采集周期与控制时段的居民不可转移负荷以及光伏发电的数据，室外温度数据来自澳大利亚政府的公开数据集［32］。售电商的售电价采用Ausgrid 公司区分夏季与冬季的分时电价［33］，具体见附录A 图A1，而购电价［34］则采用全年统一的光伏上网电价4 美分/kW。

各DER 设备的运行参数见附录A 表A1［23，35］。为描述各日用户使用DER 的多样性，本文将每日初始室内温度、EV 的出行时刻与时长、EV 和ES 的初始SOC、SA 的起始与截止运行时刻做差异化处理。上述与温度、电量相关的参数通过截断正态分布采样获得，与运行时间相关的参数通过离散均匀分布采样获得，用户主导的各类DER 运行参数的概率分布见附录A 表A2［23，35］。然后，分别从52 个星期中随机抽取一天作为测试集，其余天数为训练集。

本文仿真环境为6 核3.47 GHz Intel Xeon X5690 处理器，192 GB RAM，软件为Python3.5.2、TensorFlow1.7.0。

所采用的LSTM 神经网络提取了包含负荷、光伏发电、电价等多源时序数据未来走势的64 维特征向量，与12 维的内部状态特征（即4 种DER 设备的三元组信息）共同组成了76 维执行器和评判器网络的输入层。执行器和评判器网络结构类似，均包含2 层隐藏层，每层有100 个神经元，前者输出4 维动作（即4 种DER 设备的能量管理动作），后者输出1 维状态值函数。仿真过程中涉及的各种超参数设置见附录A 表A3。

4.2 与无模型DRL 算法的效果对比

为评估所提基于PPO 算法的能量管理优化方法，本算例先以现有文献中广泛采用的深度Q 网络（deep Q network，DQN）、深度策略梯度（deep policy gradient，DPG）和深度确定性策略梯度（deep deterministic policy gradient，DDPG）这3 种DRL 方法与本文方法作对比。

为降低结果的偶然性，每次生成10 个random seeds，每个random seed 中每个算法训练20 000 epochs，每个epoch 代表训练数据集中的一个随机日。训练过程中，每200 epoch 在测试数据集上对各DRL 算法的表现进行评估。图5 中的实线与阴影分别代表对应各DRL 算法在10 个random seed 上用测试数据集计算所得的日用电成本的平均值与标准差。

图5 4 种DRL 方法下的平均日用电成本Fig.5 Average daily electricity cost with 4 DRL methods

如图5 所示，PPO 算法在能量管理策略的训练过程中成本效益不断提升，日用电成本的标准差不断下降。最终PPO 算法下的收敛结果为372.35 美分，是4 种基于DRL 的无模型能量管理优化方法中的最低值，相比于DQN 与DPG 这2 种算法，平均日用电成本分别降低了约15.52%与8.37%，标准差分别降低了约29.35%与44.50%。其次，相较于DQN算法，PPO 算法赋能对EV、ES 和HVAC 功率的连续调节，平均日用电成本显著降低。因DPG 算法中缺少策略评估环节，策略梯度估计结果不准确且方差较大，因此导致其为收敛速度较慢的次优策略。此外，DDPG 算法由于无法处理离散动作导致策略次优，而性能依赖于对大量超参数的调节，故存在收敛困难且不稳定的现象。相比之下，PPO 算法因具备“执行器-评价器”的架构，在策略优化过程中通过计算优势值进行评估，稳定性更强。PPO 算法还通过式（27）将策略更新的目标函数进行了裁剪，简化需要满足的置信域约束，因此收敛性能更稳定、训练速度更快。

4.3 与基于模型的最优化方法效果对比

针对现有大部分文献所采用的基于模型的最优化方法所存在的局限性，为检验无模型能量管理优化方法对不确定性的应对能力，以2 种基于模型的最优化方法作为对比:

1）在假设可对不可转移负荷、光伏、温度等进行完美预测的前提下，求解最小化居民日用电成本对应混合整数线性规划（mixed-integer linear programming，MILP）［20］问题，以此作为理论最优解；

2）MPC 在每个控制时段对未来一段时间（即控制时域）的负荷和光伏等进行预测，进而在该时段上求解成本最小化问题，以所得控制序列的第1 个元素作为当前时段的控制策略，该优化过程随时间不断向后滚动。本算例以8 h 为控制时域，利用LSTM 网络进行时序数据预测。

通过求解MILP 问题得到，364.54 美分为测试日平均日用电成本的理论最优值。通过PPO 算法和MPC 获得的平均日用电成本分别为372.35 美分和384.25 美分，较理论最优解分别高出2.14% 和5.41%。这是由于MPC 虽然能够在一定程度上降低预测不确定性对成本的影响，但优化性能仍受预测误差的影响。PPO 算法不依赖于对未来信息的精准预测，并可以对数据未来走势准确感知，因此所得策略可以更好地应对不确定性。

4.4 采用LSTM 数据特征提取技术前后的效果对比

为验证所提LSTM 数据特征提取技术的有效性，将采用该技术的前后效果进行对比。结果表明，采用该技术前后的平均日用电成本分别为372.35 美分和381.83 美分，通过提取未来走势后降低了约2.48%。因此，对比于仅基于当前时段所感知的原始时序数据的策略优化［17，19-20］，所述时序数据未来走势提取技术可基于时段t之前M个时段的历史数据的时序特征，挖掘时序数据的未来趋势，以更有效地辅助智能体的序贯决策，进而提升了能量管理策略的成本效益及应对不确定性时的鲁棒性。

4.5 可泛化性（generalization）评估

为进一步验证PPO 算法下能量管理策略对未来新场景的泛化性和鲁棒性，在PPO 算法训练完成后，算例选取了测试数据集中夏季与冬季2 个典型日来分析能量管理策略的成本效益。对应于夏季典型日的可调节DER 设备的运行情况、室内与室外温度、用户净负荷/发电的情况分别如附录A 图A2、图A3、图A4 所示。图A5、图A6、图A7 则展示了冬季典型日中可调节DER 设备的运行情况、室内与室外温度、用户净负荷/发电的情况。

在夏季典型日中，附录A 图A2 与图A3 呈现出较高的室外温度以及充足的光伏发电特征。因早晨温度较低，HEMS 并未启动HVAC，而是在08:30 以后启动，由于室外温度超过阈值，HVAC 尽可能吸收光伏发电量，在保持室内温度恰好低于24 ℃的同时减小用电成本。此外在11:00—14:30 之间，售电商购电价格仍高于售电价格时，HEMS 尽可能选择利用ES 的充电来吸收剩余的光伏发电量，而非将其出售。此外，SA 的运行周期被转移到了售电价格较低的时段22:30—24:00。如图A4 所示，所得的能量管理策略通过利用DER 设备的互补性（如EV与ES），在09:00—20:30 之间实现了用户净负荷为0，完成了光伏的充分消纳，在最大限度上挖掘了DER 设备的灵活性。

冬季典型日与夏季典型日的区别在于较低的室外温度与光伏发电量，如附录A 图A5 和图A6 所示。在图A5 中，因早晨温度过低，HEMS 启动HVAC 的制热功能以保证温度略高于19 ℃，07:00之后电价升高后关闭HVAC 以降低成本。与夏季典型日相同的是，SA 的运行周期同样被转移到了售电价格较低的时段。HEMS 选择在用电低谷时段向ES 与EV 充电，在07:30—11:30 与14:00—20:30这2 个用电高峰时段通过ES 与EV 放电以满足用户电能需求，在07:30—22:00 之间实现了用户净负荷接近于0。

5 结语

本文研究了面向居民用户的实时自治能量管理优化方法。在避免对用户DER 设备进行精确建模的基础上，提出了可描述多类型DER 设备运行特性的三元组信息，明确设备动作，将实时能量管理优化问题建模为序贯决策问题。所提方法不依赖于对未来信息的准确预测，仅靠实时感知环境状态进行自趋优式策略学习。所采用的LSTM 神经网络通过挖掘智能电表所采集多源时序数据的时序特征，准确感知未来走势。此外，PPO 算法赋能在多维连续-离散混合的动作空间中高效学习最优能量管理决策。

算例结果表明，本文所提方法能够综合考虑电价、室外温度、光伏出力、用户行为等不确定因素，充分挖掘柔性负荷的灵活性，实现对多类型DER 设备的实时最优能量管理。与此同时，在对比其他3 种无模型DRL 算法和2 种基于模型的最优化方法后，PPO 算法在收敛性、最小化用户成本以及应对不确定性表现等方面均具有更好的表现。

本文研究重点在于用户与电网之间的优化调控问题，并不涉及不同用户之间的电力交易，下一步研究将考虑用户与用户之间、用户与电网之间的分层联合优化调度。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。