基于局部离群因子的PMU 连续坏数据检测方法
2022-01-11朱世佳毕天姝
刘 灏,朱世佳,毕天姝
(新能源电力系统国家重点实验室(华北电力大学),北京市 102206)
0 引言
同步相量测量单元(synchrophasor measurement unit,PMU)因其同步性、快速性和准确性,已成为实现状态感知的重要装置[1]。此外,PMU 可以为决策控制、振荡检测和状态估计[2-4]等应用提供数据。截至2018 年,中国已安装投运了约3 000 台PMU,覆盖全部220 kV 及以上电压等级变电站、发电厂和大部分并网可再生能源发电机组[5]。2017 年底,北美也安装了约2 500 台PMU[6]。
然而,受通信拥塞、干扰和网络攻击等诸多因素的影响,PMU 存在不同程度的数据质量问题[7]。北美约10%~17%的PMU 数据存在质量问题[8],这一比例在中国高达20%~30%。PMU 数据质量问题严重制约其在电网监测、保护与控制等应用中的运行效果。尤其是连续坏数据与扰动数据高度相似,可能会导致控制中心做出错误的决策,甚至威胁系统安全。因此,准确检测PMU 连续坏数据至关重要。
目前检测PMU 坏数据的方法主要有模型驱动和数据驱动两大类。文献[9]给出了一种结合卡尔曼滤波和平滑算法的时间序列预测模型来检测坏数据。文献[10]提出了一种基于无迹卡尔曼滤波器并结合状态估计的方法,实时检测坏数据。文献[11]提出了一种鲁棒的广义估计量,根据测量的时间相关性和统计一致性来检测坏数据。基于模型的方法都需要系统拓扑和线路参数的先验知识,因此,若系统拓扑参数未知或存在偏差,2 种方法的效果都会受到影响。
数据驱动的方法近年来受到广泛关注。文献[12]以神经网络的加权输出残差作为聚类特征,再采用距离代价函数的K 均值算法来检测坏数据。文献[13]对误差序列进行聚类,并利用间隙统计算法确定最佳聚类个数,从而对坏数据进行识别。文献[14]提出了一种集成学习算法来检测坏数据。这些方法仅适用于静态数据中的异常检测。
文献[15]构造了双层长短期记忆网络,通过分解重构误差检测坏数据。文献[16]提出了一种基于主成分分析的方法来检测坏数据,利用低维主成分对扰动敏感、高维主成分对坏数据敏感的特征来区分扰动数据。文献[17]基于四点斜率特征构造决策树区分扰动数据和坏数据。但是这些方法均是有监督的,存在离线训练的负担。
文献[18]提出了一种基于时空相似性的方法在线检测坏数据。文献[19]构造了Hankel 矩阵,通过随机置换数据矩阵的列,并对置换前后Hankel 矩阵的秩进行比较来区分坏数据和扰动数据,其本质是利用置换后数据时间相关性丢失这一性质进行区分。上述方法对扰动过程中攻击注入的动态相关性强的连续坏数据可能不适用。
因此,本文提出了一种无监督的基于动态时间规整(dynamic time warping,DTW)和局部离群因子(local outlier factor,LOF)的检测方法。该方法能在区分扰动数据的同时,有效检测历史数据攻击这类更隐蔽攻击以及存在次同步振荡的连续坏数据。
1 基于DTW 的空间相似性评估方法
1.1 连续坏数据和扰动数据的特征
本文主要研究因通信拥塞、干扰或网络攻击等导致的PMU 连续坏数据。在正常或扰动条件下,所有良好的PMU 数据本质上为同一电网不同物理位置的PMU 量测序列。因此,相近位置获得的良好PMU 数据往往具有相似的动态行为,因为代表了相同的底层物理系统动态。然而,坏数据被认为是由其他数据源生成,因此具有不同的动态特性[20]。以PMU 幅值数据为例,现场实测扰动数据、连续坏数据和正常数据之间的对比如图1 所示。
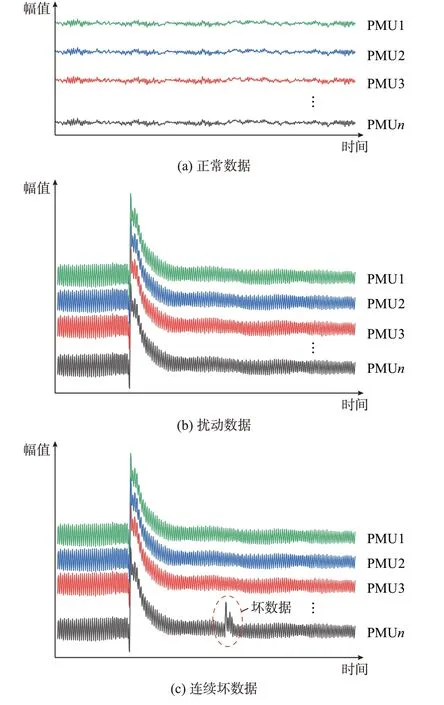
图1 实测扰动数据、连续坏数据以及正常数据比较Fig.1 Comparison of measured disturbance data,continous bad data,and normal data
图1 中PMU1、PMU2、…、PMUn分别为邻近的第1 台PMU、第2 台PMU、…、第n台PMU。由图1可以看到,在出现扰动时,虽然数据表现出时序异常,但在扰动过程中多台PMU 数据表现出相同的波动趋势。而出现坏数据时,个别PMU 数据不仅时序异常,而且在空间上也和其他PMU 数据不同。
基于上述分析可知,在正常和扰动运行条件下,PMU 坏数据与其相邻PMU 良好的数据具有弱时空相关性,因此可以视为时空异常值;PMU 连续坏数据在同一时间窗内具有弱空间相似性,而扰动数据具有强空间相似性。因此,根据这一特性可在线识别连续坏数据,并保证扰动数据不被误判。
值得注意的是,弱时空相关性的特征也适用于协同网络攻击。假设攻击者只有有限的资源,只能在短时间内攻击一小部分PMU。与系统物理扰动可能会影响在本地区域内获得的大量PMU 数据不同,资源有限的攻击者只能操作有限数量的PMU。因此,部分协同攻击下的PMU 数据也与其相邻的无攻击数据保持微弱的时空相关性。
1.2 空间相似性评估方法
扰动数据表现出强的空间相似性,而连续坏数据表现出弱的空间相似性。DTW 的优势是在2 个时间序列长度不一致时(例如1 台PMU 出现数据丢失),仍能很好评估相似性。采用相关系数法计算协方差时需要2 个PMU 序列长度一致,且相关系数接近1 的程度受PMU 数据量的影响。因此,本文利用DTW 距离来衡量2 台PMU 的空间相似性。
DTW 算法采用动态规划的思想,通过调整PMU 序列中不同时刻对应元素之间的关系,找到一条最优弯曲路径,使路径的距离最小,从而评估PMU 序列之间的关系[21]。DTW 路径示意图如图2所示。给定2 台PMU 数据X={x1,x2,…,xn}和Y={y1,y2,…,ym},X和Y可以同为电压幅值或频率。本文以幅值为例,构造了距离矩阵Dn×m,其元素D(i,j)为:
式中:xi和yj分别为第i个测量点和第j个测量点的相量幅值;n和m分别为第1 台和第2 台PMU 数据的测量点数。
式(1)表示2 台PMU 数据点xi和yj的欧几里德距离。矩阵D中每组相邻元素(图2 中S1和S2)的集合称为弯曲路径,需要满足边界性、连续性和单调性的约束[22]。满足上述约束条件的弯曲路径有多条。弯曲路径可以表示为P={p1,p2,…,ps,…,pk},其中k是路径中元素的总数,元素ps是路径上点s的坐标,即ps=(i,j),其中i和j分别为不同PMU 的测量点。
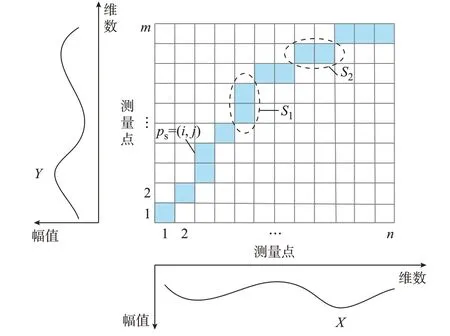
图2 DTW 路径示意图Fig.2 Schematic diagram of DTW path
DTW 的目的是找到一条最优的弯曲路径,使PMU 数据X和Y的弯曲总代价最小,即找到一条最短路径(如图2 中蓝色实心方块所示的路径):
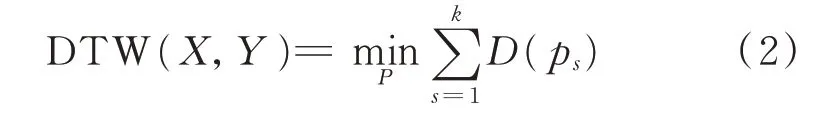
式中:DTW(X,Y)为被用来计算PMU 数据X和Y距离的函数。
DTW 距离越小,表示2 台PMU 数据间的空间相似度越高。利用式(2)可以评估任意1 台PMU 数据与所研究系统中其他PMU 数据在一段时间窗内的空间相似性,以此作为区分扰动数据和连续坏数据的特征。
2 连续坏数据检测方法
使用上面的过程能够提取出可区分连续坏数据和扰动数据的空间特征。在一段时间窗内空间相似性强的数据将被视为正常(扰动)数据,空间相似性弱的PMU 数据被确认为在当前窗口存在坏数据的PMU。如何根据所研究系统中任意2 台PMU 计算得到空间相似性矩阵,并得到每台PMU 的异常情况就成为难点。本章拟通过计算任意2 台PMU 空间相似性的比值作为2 台PMU 的距离,进一步基于密度得到每台PMU 的异常分数(LOF 值)。
2.1 基于LOF 的不良数据检测方法
LOF 法是基于密度的方法,它旨在发现数据集中异常模式。异常与否,取决于样本点与周围邻居的密度比。在本文所研究的问题中,LOF 法中的样本点即空间内每台PMU,通过计算每台PMU 和它相邻PMU 的密度比值来判断任意1 台PMU 在空间上的异常程度。
图3 中,每个点表示空间中不同位置的PMU。C1和C2代表正常PMU 簇;O1和O2代表离群的异常PMU。由图3 可知,如果1 台PMU 的密度比较小,而它周围临近PMU 的密度比较高,那么它越离群(例如图中的O1),从而成功选出空间相似度弱的PMU。
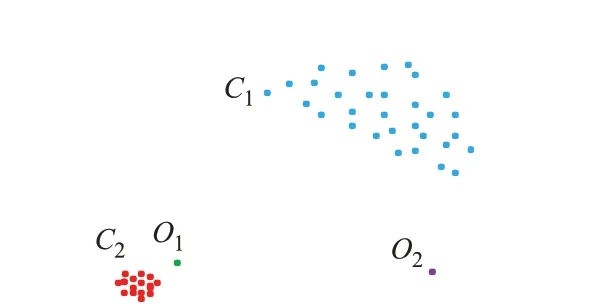
图3 LOF 示意图Fig.3 Schematic diagram of LOF
在LOF 法中,通过给每台PMU 都分配1 个依赖于邻域密度的LOF 值,可以判断该台PMU 是否为空间异常。对图3 中任意2 台PMU 的距离定义如下:
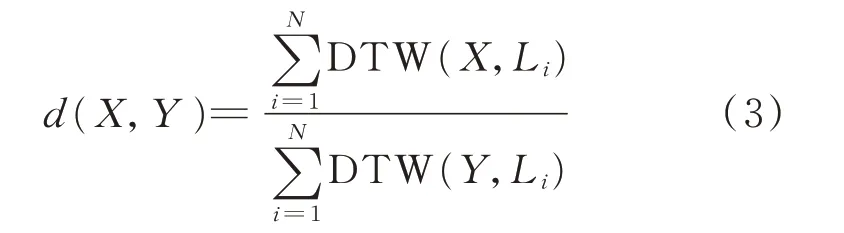
式中:N为所研究系统中PMU 的台数;Li为第i台PMU 数据。
式(3)将基于DTW 算法求得的任意1 台PMU与其他PMU 的平均距离作为其空间特征,2 台PMU 的空间相似性的比值作为LOF 法里任意2 台PMU 的距离,从而便于挑选出空间相似性弱的点(离群点)。
在式(3)的基础上,可计算每台PMU 的LOF值,见附录A。LOF 值超过阈值被认为是坏数据,由此实现正常或扰动数据和连续坏数据的划分。
2.2 基于箱线图的阈值确定法
在一个平稳的扰动数据集,LOF 值为2 可能就是一段坏数据,而在一个强烈波动的数据集里,LOF 值为5 可能仍然是一个正常值,所以简单地采用一个常数作为阈值明显不合理。本文提出了一种基于箱线图的阈值确定法,根据PMU 数据集的整体波动情况灵活设定阈值。
箱线图是一种用作显示一组数据分散情况的统计图,是利用数据中的5 个统计量(最小值、上四分位数、中位数、下四分位数、最大值)来描述数据的一种方法。箱线图示意图如图4 所示。图4 中,上四分位数、下四分位数指的是一组LOF 值按从小到大顺序排列后,处于25%、75%位置的数值。由于本文中LOF 值越大表明该台PMU 空间相似性越弱,在当前窗口越有可能存在坏数据,因此设定阈值如下:
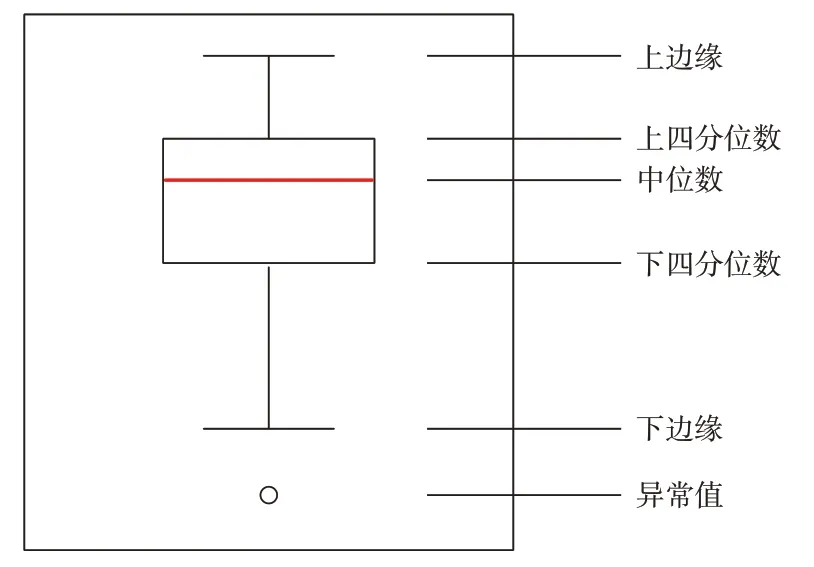
图4 箱线图示意图Fig.4 Schematic diagram of box-plot

式中:η为阈值;Q3和Q1分别为1 组LOF 值里的上四分位数和下四分位数;IQR=Q3-Q1,为上四分位数和下四分位数的差值。
箱线图提供了识别异常LOF 值的一个标准:异常值被定义为大于Q3+3IQR的值。这与经典的3σ准则不同,3σ 准则是以数据服从正态分布为前提,但实际数据往往并不严格服从正态分布。而且均值和标准差的耐抗性极小,异常值本身会对它们产生较大影响。显然,非正态分布数据中判断异常值,其有效性是有限的。箱线图依靠实际数据,不需要事先假定数据服从特定的分布形式,它只是真实直观地表现数据形状的本来面貌;另一方面,箱线图判断异常值的标准以四分位数为基础,四分位数具有一定的耐抗性,所以异常值不会对这个标准产生影响,箱线图识别异常值的结果比较客观。
值得一提的是,箱线图中内限是Q3±1.5IQR,外限是Q3±3IQR,超过内限是有可能异常的LOF 值,超过外限是绝对异常LOF 值。本文选择超过外限是因为实际上不同位置PMU 数据的空间相似性可能不严格很强,因此外限作为阈值能适度避免误判。
2.3 连续坏数据检测方法整体流程
所提算法的流程如图5 所示。首先,利用前一段干净数据时间窗的平均值进行标准化处理,消除各PMU 自身的影响;然后,采用不同PMU 数据的DTW 距离作为特征量进行空间相似性分析;最后,基于LOF 法和箱线图对连续坏数据进行检测。由于三相短路过程中不同母线相量幅值下降深度差异较大,有可能引起误判,因此,为了避免对三相短路扰动的误判,整体流程中在LOF 值与设定阈值比较后又增加了判据:是否超过半数PMU,其当前窗口数据的最大相邻差值Kt( =(zt-zt-1)/zt)大于0.2,其中zt和zt-1分别为时刻t和时刻t-1 的数据。
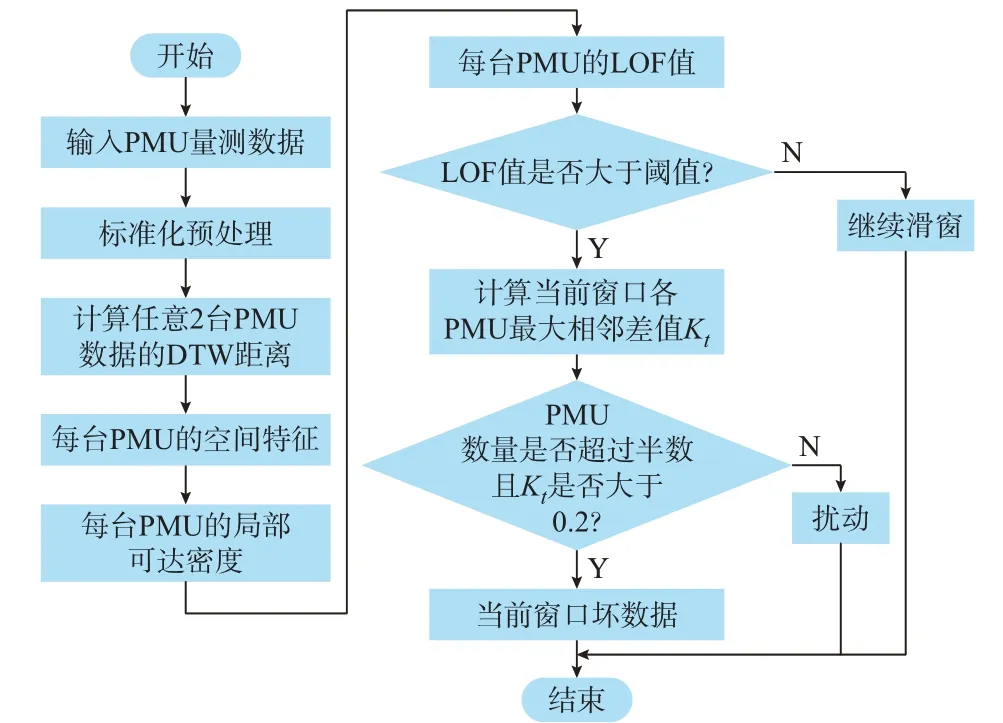
图5 连续坏数据检测算法流程图Fig.5 Flow chart of detection algorithm for continuous bad data
3 算例分析
对本文所提方法进行了验证,并且将结果与文献[18]中时空相似性的方法进行了比较。
3.1 仿真测试
采用IEEE 10 机39 节点系统对不同扰动条件下的仿真信号进行了测试。窗长为40 个数据点(0.4 s)。在三相断线后设置一段偏差为0.09%的斜坡类型的连续坏数据,本文方法和文献[18]中的方法均能检测,见附录B。
切机后注入偏差为0.15%的历史扰动坏数据,这是目前更难检测到的一种攻击方式,如图6所示。
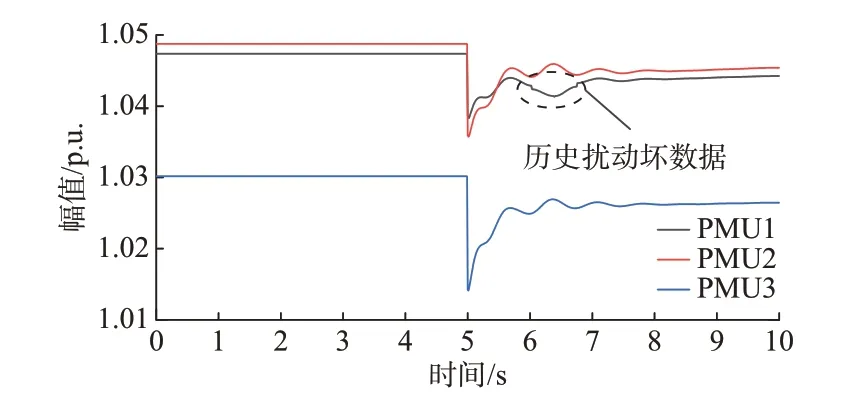
图6 历史扰动坏数据Fig.6 Historical disturbance bad data
利用所提方法和文献[18]中的时空相似性的方法对图6 中坏数据进行检测,检测结果如图7 所示。由图7 可知,所提方法能检测到PMU1 中历史扰动坏数据,但是时空相似性的方法无法有效检测。原因是文献[18]中时空相似性方法基于不同母线标准化后的方差计算LOF 值,而基于标准化方差的方法仅表示数据时间上前后波动幅度的变化,有些明显是坏数据但波动幅度前后变化不明显的坏数据无法有效检测。
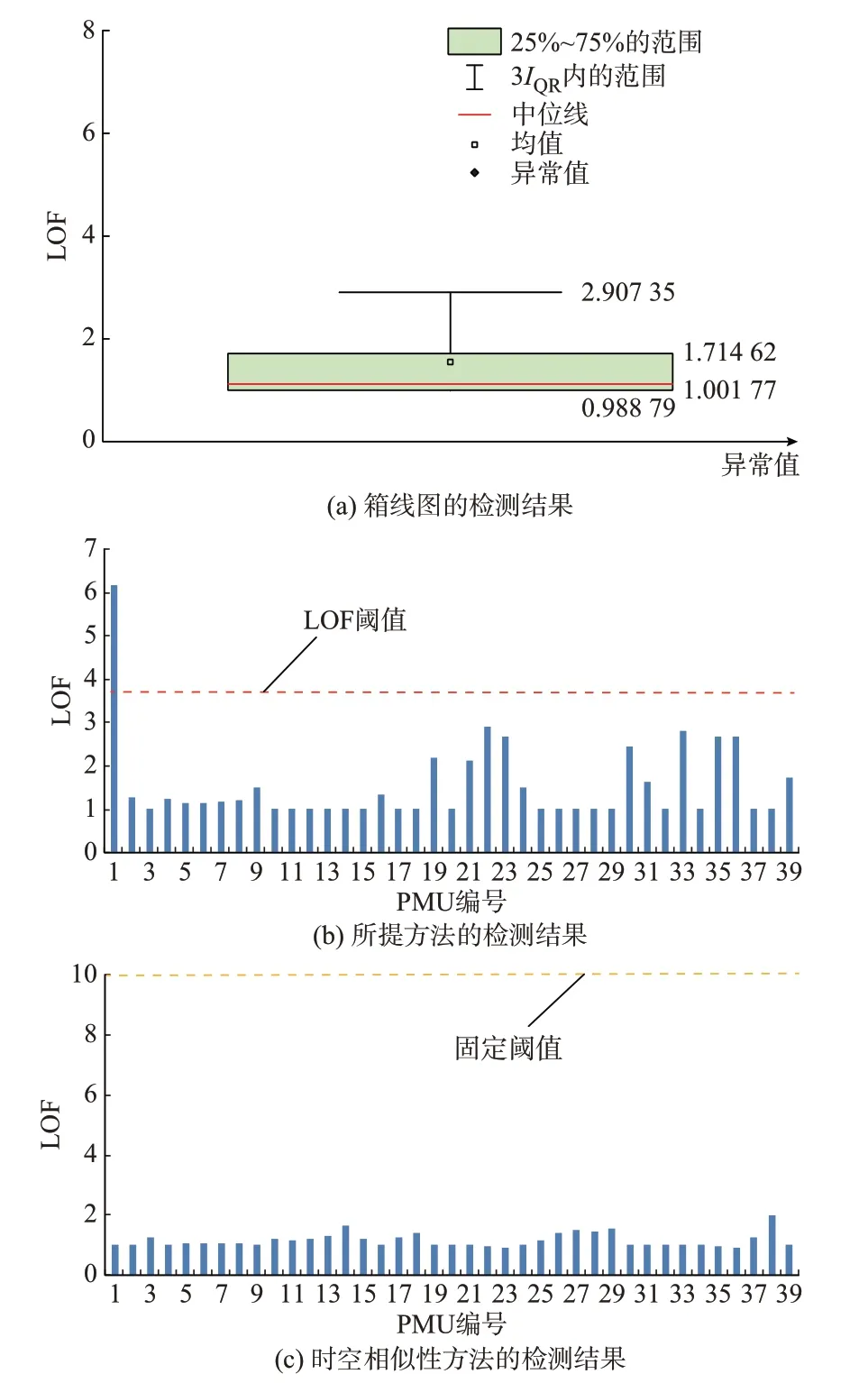
图7 历史扰动坏数据的检测结果Fig.7 Detection results of historical disturbance bad data
为验证所提方法的有效性,与文献[18]中方法进行了在不同坏数据偏差下的对比实验,每种偏差下设置了5 种不同坏数据类型,共20 组检测结果,准确率如表1 所示。

表1 两种方法准确率对比Table 1 Comparison of accuracy between two methods
由表1 可知,所提方法对偏差为0.2%及以上的坏数据有较高准确率,而文献[18]中方法对于偏差0.2%的坏数据检测效果变差,原因是太小偏差的连续坏数据和其他母线正常的扰动数据标准差相差不大。因此,所提方法在检测范围和整体准确率上相较于文献[18]中方法有一定优势。
为测试所提方法在输入信号中含有噪声时的有效性,采用IEEE 10 机39 节点系统在切负荷后的仿真数据加60 dB 高斯白噪声对所提方法和文献[18]方法进行了验证(因为输电网噪声一般在60 dB[23])。在含噪声下设置了4 组不同偏差的斜坡攻击坏数据,所提方法和文献[18]中方法的检测结果如表2所示。
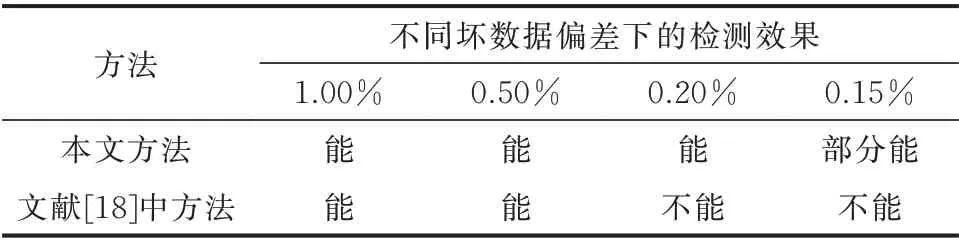
表2 两种方法的检测结果对比Table 2 Comparison of detection results between two methods
由表2 可知,所提方法对信号中含噪声坏数据的识别效果要优于文献[18]中的方法,但对于有噪声和存在偏差0.15%的坏数据,所提方法也仅能识别少数,存在漏判的问题,60 dB 噪声造成的数据偏差最大达0.3%,会影响坏数据辨识结果。噪声的存在确实会使小偏差的坏数据淹没在噪声里而难以检测。
3.2 PMU 实测数据验证
利用中国西部地区实测数据来验证所提方法的有效性。加入偏差为0.5%的尖峰坏数据(如图8 所示)和偏差为0.2%攻击注入的连续坏数据(如图9所示),利用LOF 值和箱线图法设定的阈值比较后的检测结果分别如图10 和图11 所示。
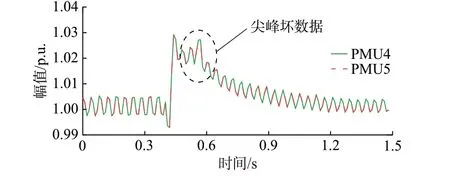
图8 带尖峰的实测数据Fig.8 Measured data with spikes
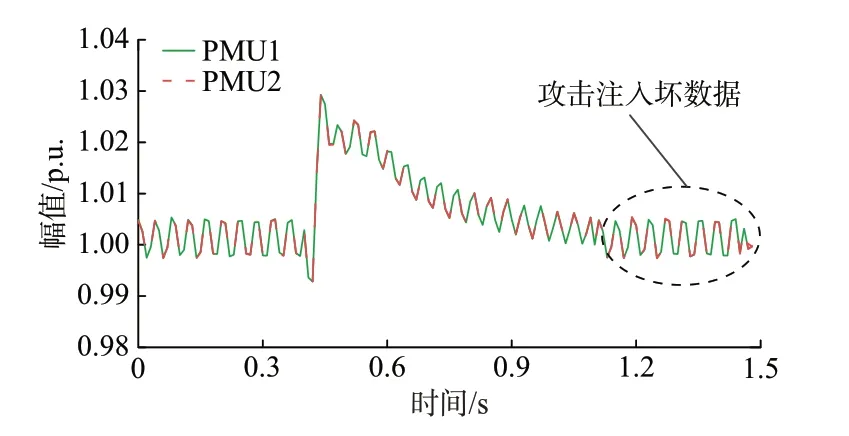
图9 存在攻击注入的实测连续坏数据Fig.9 Measured continuous bad data with attack injection
图10 显示,当尖峰数据的偏差小于0.6%时,文献[18]中的时空相似性方法无法对其进行有效检测。所提方法可有效检测实测数据中偏差为0.5%的连续尖峰坏数据。原因可能是文献[18]中的方法基于方差的特征不明显。
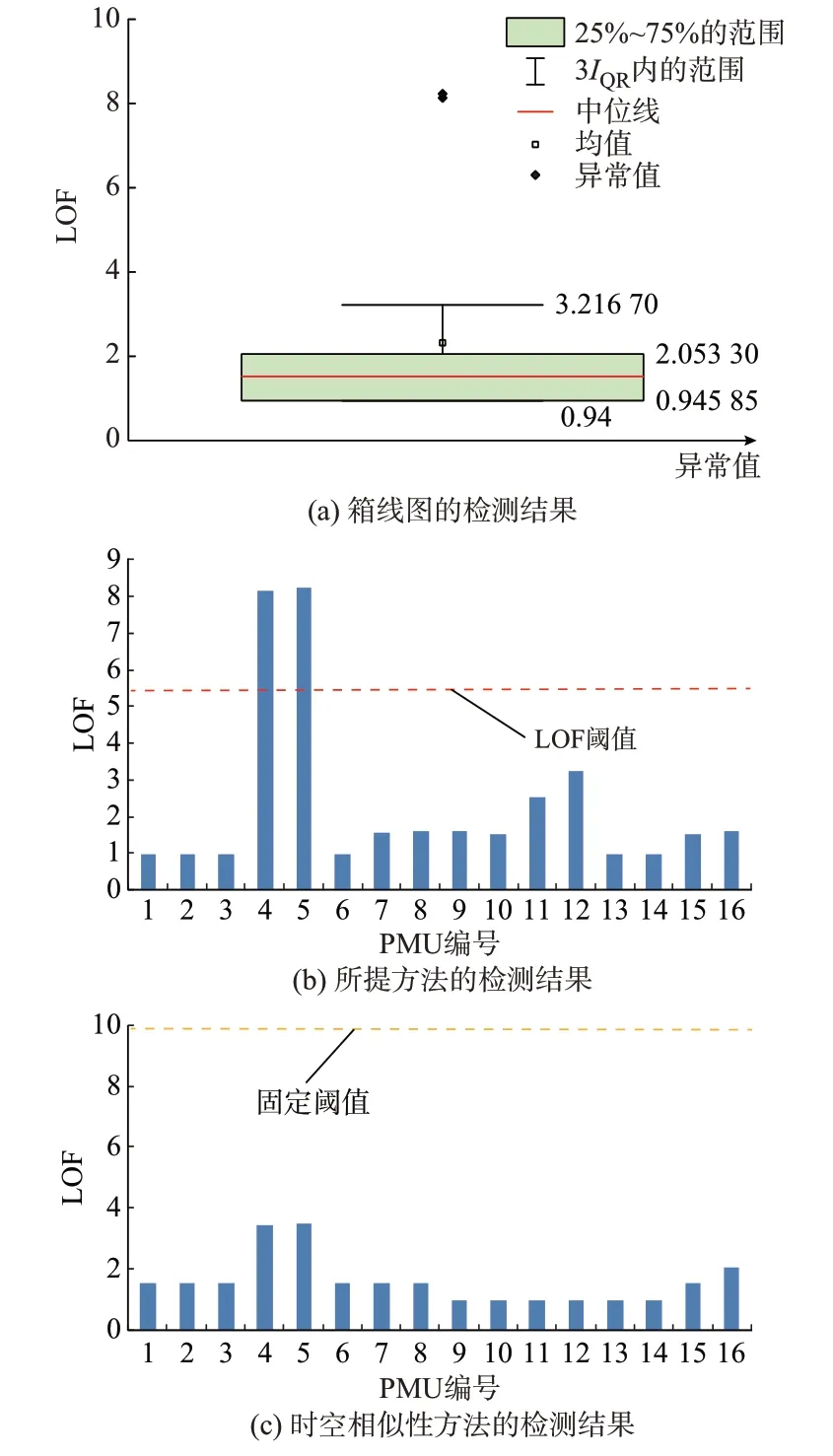
图10 实测尖峰数据的检测结果Fig.10 Detection results of measured spike data
图11 表明,当攻击注入历史扰动数据作为坏数据时,时空相似性方法无法检测,原因是次同步振荡数据本身存在一定方差,注入的PMU 数据和没有注入的PMU 数据方差相差不大,因此基于方差做差或者方差做比来定义2 台PMU 的距离检测不到坏数据。而所提方法基于数据波动趋势建立相似性的比值作为2 台PMU 的距离,可以检测到空间波动趋势不一致的攻击数据。由此可见,文献[18]中的时空相似性方法仍有一定的局限性,而本文所提方法可满足系统不同类型连续坏数据的检测要求。
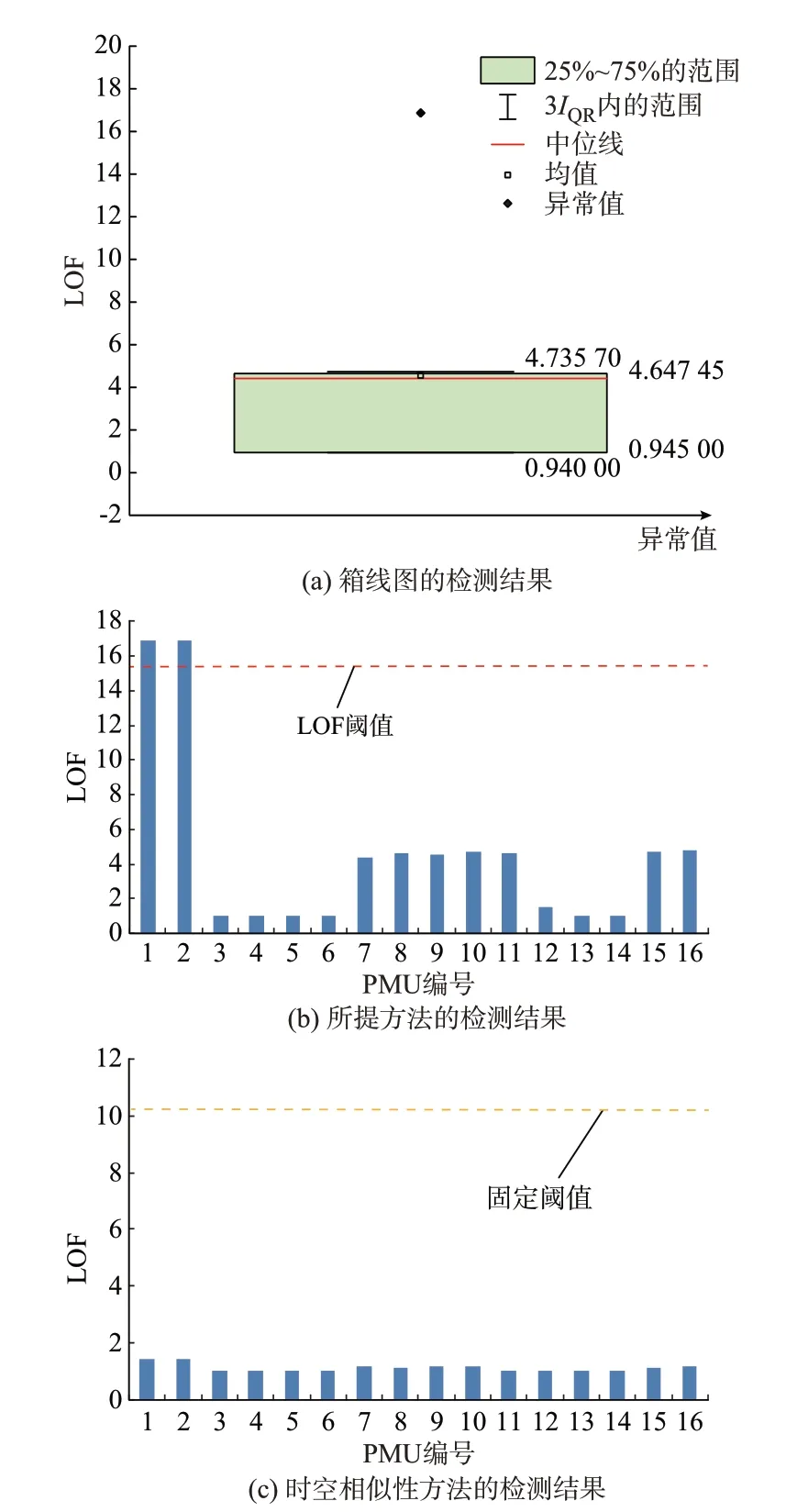
图11 实测连续坏数据的检测结果Fig.11 Detection results of measured continuous bad data
4 结语
本文提出了一种数据驱动的在线PMU 连续坏数据检测算法。它没有离线训练的负担,且能避免对扰动数据的误判,并可以提高PMU 数据的质量,为PMU 在电力系统中的各类应用提供数据基础。得到主要结论如下。
1)提出了一种基于DTW 的衡量PMU 数据空间相似性方法。通过计算不同PMU 数据的DTW距离,提取了区分扰动数据和连续坏数据的空间特征。
2)利用LOF 法对连续坏数据进行检测。它能够在线检测出扰动过程中的连续坏数据,而现有方法则不易检测。
3)提出了基于箱线图的阈值确定方法,与其他方法相比,解决了单一固定阈值对不同波动情况的PMU 数据集设置不合理的问题。
4)仿真和现场数据测试证明了所提方法对连续坏数据的识别和检测是有效的,可以为电力系统提供高质量的PMU 数据。
本文未考虑大量PMU 在同一时间段存在攻击注入连续坏数据的情况。下一步将对更多PMU 遭受同一类型攻击引起的连续坏数据进行深入研究。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
