海上风电超大直径单桩基础水平位移计算影响因素研究

张强林，吴衍剑，张祥龙

(中国电建集团福建省电力勘测设计院有限公司，福建 福州 350003)

为改善我国能源结构，实现社会经济可持续性发展，在我国沿海风能资源丰富区，目前正大力发展海上风电工程，主要采用的基础型式有单桩基础、高桩承台基础、导管架基础等。

单桩基础结构主要为通过将一根超大直径单桩(最大直径7～8米)打入海底土层一定深度来维持整体结构的稳定和变形要求，型式简单，是目前最为常用的海上风电基础型式之一，在江苏、广东等地多个海上风电场均有使用。

海上桩基的水平位移计算通常采用p-y法，根据经验p-y法对于较小直径桩(如桩径2 m左右)的水平位移计算较为精确，但对于这种超大直径单桩由于尺寸效应影响，应用p-y法存在一定的误差。为解决这个问题，通常是采用三维有限元软件，考虑桩-土相互作用通过对单桩基础结构整体建模进行计算与分析，而三维数值模拟计算所得到的结果是否可靠主要取决于模型相关参数的设置[1]。本文以莆田海域某风电场项目中一个采用单桩基础形式的机位作为研究对象，以大型有限元软件ABAQUS为工具，通过对整体模型的静力计算，分别对土体本构关系、土体物理参数(如土体弹性模量、内摩擦角、土体剪胀角)以及桩-土接触模型设置等与泥面位置水平位移计算相关的参数展开敏感性分析，以确定位移计算的主要影响因素。通过此分析便于为后续类似工程的单桩基础结构设计提供参考。

1 工程背景资料

风场理论水深15～25 m，设计高水位3.34 m，设计低水位为-2.95 m，50年一遇极端高水位和低水位分别为4.80 m和-4.05 m。风机采用上海电气7 MW风电机组，风场某机位地勘钻孔资料、土层分布以及地勘提供的部分土层物理力学参数建议值如表1所示。

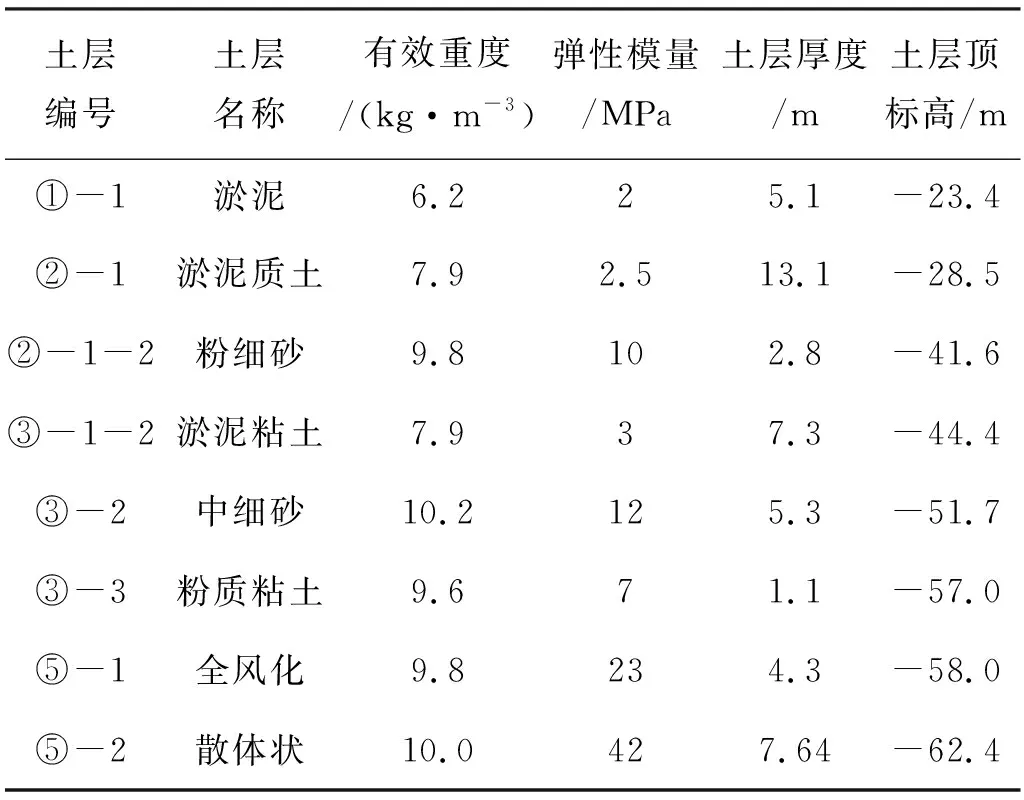
表1 土层分布及物理力学参数建议值

针对此机位钻孔条件，实际工程中是按无过渡段的大直径单桩基础结构进行设计，设计方案为：钢管桩桩顶标高为16.0 m，桩端标高为-70.0 m，泥面处标高为-23.4 m，桩基基础埋深为46.7 m。钢管桩上部与塔筒底部连接处的桩身直径为6 m，钢管桩底部直径为7.8 m，桩身中部通过变直径椎体进行过渡连接。钢管桩材质及力学参数如表2所示。

表2 钢管桩材质及力学参数

2 单桩基础结构整体有限元数值分析模型

2.1 有限元模型

根据地勘资料及桩体参数，采用大型有限元软件ABAQUS实体单元建立整体分析的有限元模型，如图1所示。

图1 有限元数值模拟计算模型示意图

其中钢管桩与土体均采用C3D8R单元模拟，桩土之间采用接触面模型。在桩-土接触面附近的网格进行加密处理，对于远离接触面的土体模型边界处网格适当加粗处理。

计算基准模型中钢管桩视为理想弹性材料，土体结构采用Mohr-Coulomb弹塑性本构模型。桩-土接触面采用主-从(Master-Slave)接触算法，以桩体为主面，土体为从面，接触面切向按库伦罚函数模型设置，滑动摩擦系数取桩与土层摩擦角的正切值，接触面的法向属性设置为硬接触。

为了避免土体边界效应对于计算结果的影响，模型周边土层按半径50 m圆柱体设置，土层高度为100 m。周边土体径向位移约束，土体底部固定。

2.2 荷载组合

本次研究的工况组合依据《海上风电场工程风电机组基础设计规范》(NB/T 10105-2018)确定，主要考虑风机荷载与波流荷载，选取正常使用极限工况进行变形计算，其中风机荷载为主要荷载，波流荷载为次要荷载。正常使用极限工况下的荷载设计值如表3所示。此荷载作用沿水平轴正向作用于结构模型上。

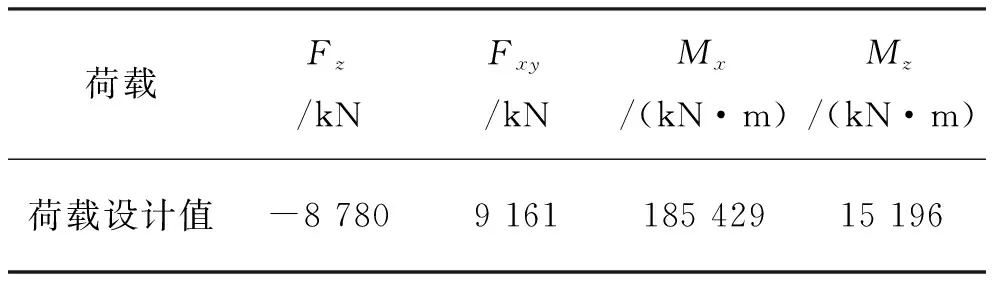
表3 正常使用极限工况的荷载设计值

3 单桩基础结构变形计算影响参数敏感性分析

针对ABAQUS软件所建立的整体模型，采用控制变量法(即仅改变目标参数的取值，其余参数设置保持不变)，对诸如土体本构关系、土体物理参数(如土体弹性模量、内摩擦角、土体剪胀角)以及桩-土接触模型设置等对单桩变形计算有影响的因素分别进行了敏感性分析，以探讨影响水平变形计算的主导因素，以便在后继工程应用中重点考虑。

3.1 土体本构关系

在保持其他参数不变的前提下，分别选用弹性本构以及Mohr-Coulomb弹塑性本构作为土体模型进行计算，所得到的钢管桩桩身水平位移曲线如图2所示。

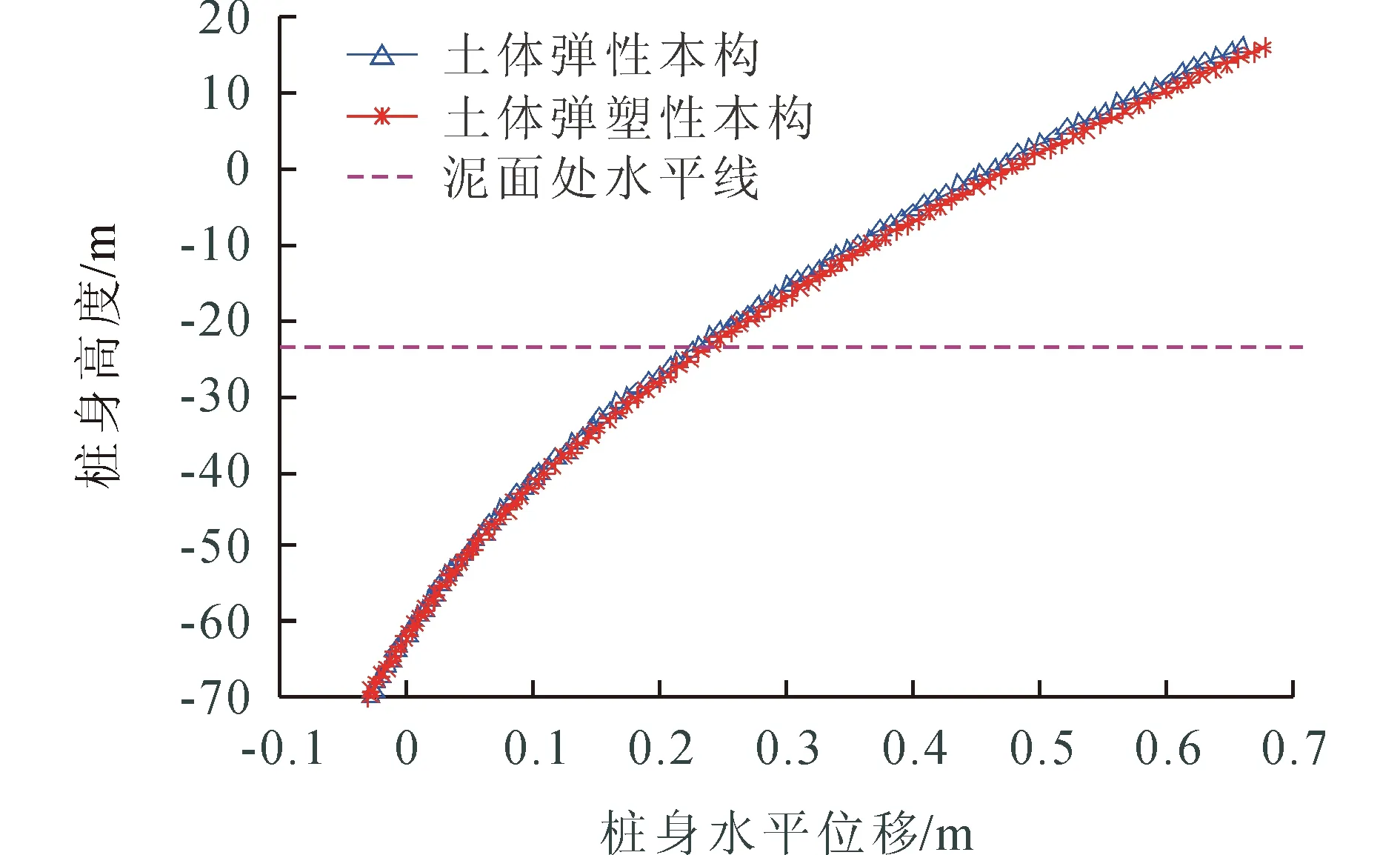
图2 不同土体本构模型下钢管桩水平位移曲线

可以看出，当考虑土体为弹塑性本构模型时，钢管桩桩身的变形均要大于土体为弹性模型时，此时，钢管桩桩身泥面处的水平位移分别为0.241 4 m与0.233 2 m，弹塑性变形相较于弹性变形大约3.4%。

3.2 土体弹性模量

土体弹性模量的数值大小代表了土体抵抗弹性变形的能力强弱，采用控制变量法，除弹性模量外保持其余输入参数不变，图3给出了分别取1～5倍的弹性模量时，钢管桩桩身泥面处水平位移以及转角随弹性模量变化的关系图。

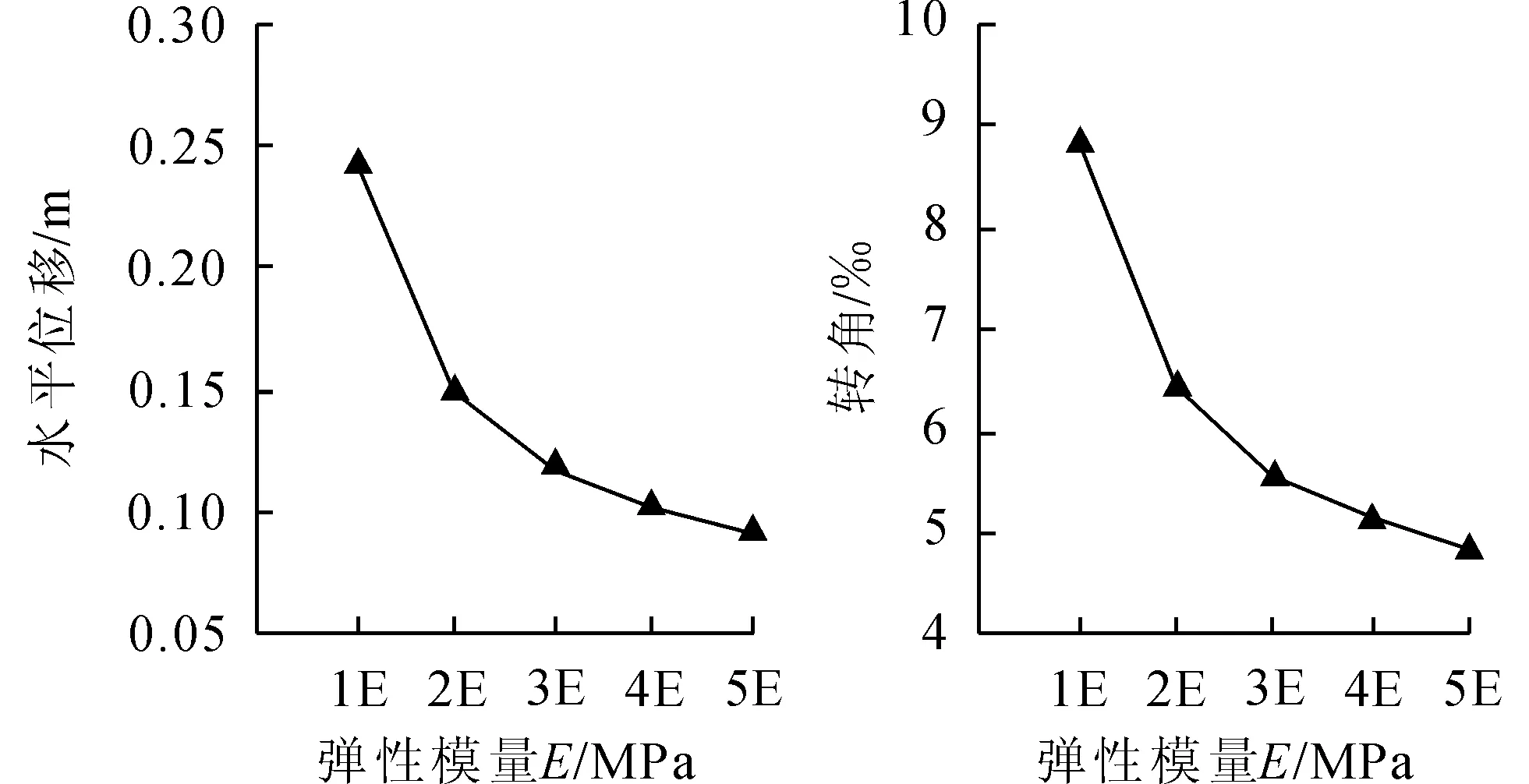
图3 钢管桩泥面处水平位移及转角随弹性模量变化关系图

可以看出，随着弹性模量增大，钢管桩泥面处变形呈现明显下降趋势，当弹性模量由1倍增加至2倍时，水平位移及转角出现大幅度下降，其中，水平位移值由0.241 4 m下降至0.149 6 m，降幅为38.0%，转角值由8.82‰下降至6.43‰，降幅为27.1%，当弹性模量继续增大时，变形值降幅减小。

3.3 土体内摩擦角

土体采用Mohr-Coulomb弹塑性本构模型计算时，所输入的内摩擦角是影响土体抗剪强度的重要参数[2]。在工程地勘报告中，对于内摩擦角的建议值通常包含下限值、中间值以及上限值，各区间差值约为3°～4°，在不改变其余土体模型参数的前提下，分别采用三种内摩擦角(下限值、中间值、上限值)进行计算，结果如图4所示。

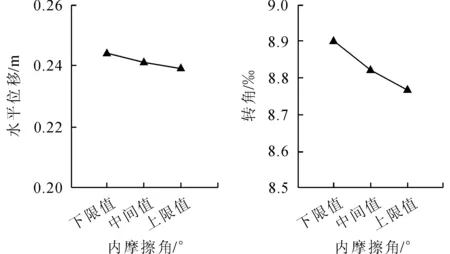
图4 钢管桩泥面处水平位移及转角随内摩擦角变化关系图

可以看出，随着土体的内摩擦角增大，钢管桩桩身泥面处的水平位移与转角逐渐减小，当内摩擦角分别取下限值以及上限值时，水平位移值由0.244 3 m下降至0.239 3 m，降低幅度约为2.0%，转角值由8.90‰下降至8.77‰，降低幅度约为1.6%。

3.4 土体剪胀角

土体的剪胀性是指土体在剪切过程中，由于颗粒间相对位置的变化而引起土体体积的变化，由此来表征土体的塑形应变状态[3-4]。

本次计算剪胀角的取值分别为0.1°、3.0°和7.0°，其余模型参数保持不变，计算结果如图5所示。

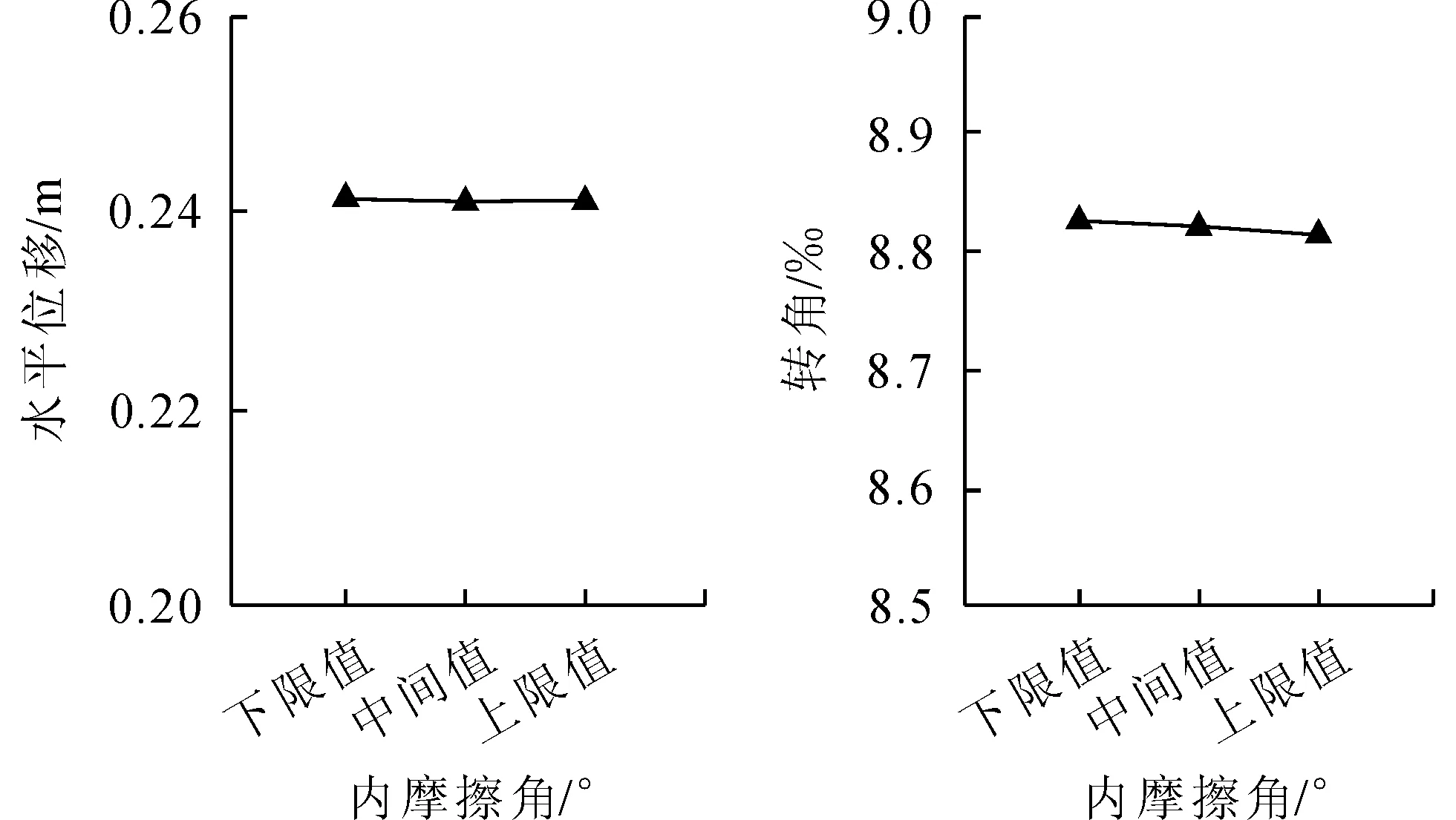
图5 钢管桩泥面处水平位移及转角随剪胀角变化关系图

可以看出，随着剪胀角增大，泥面处位移以及转角计算值逐渐较小，但降低幅度较低，当剪胀角从0.1°增加至7°时，土体的位移值由0.241 5 m下降至0.241 2 m，转角值由8.83‰下降至8.81‰，两者降幅约为0.14%。

3.5 桩-土接触模型

本次计算考虑两种接触面的模型：①摩擦接触，允许桩-土接触面发生脱开；②绑定约束，不考虑桩-土接触面脱开[5]。两种接触模型下的计算结果如图6所示。

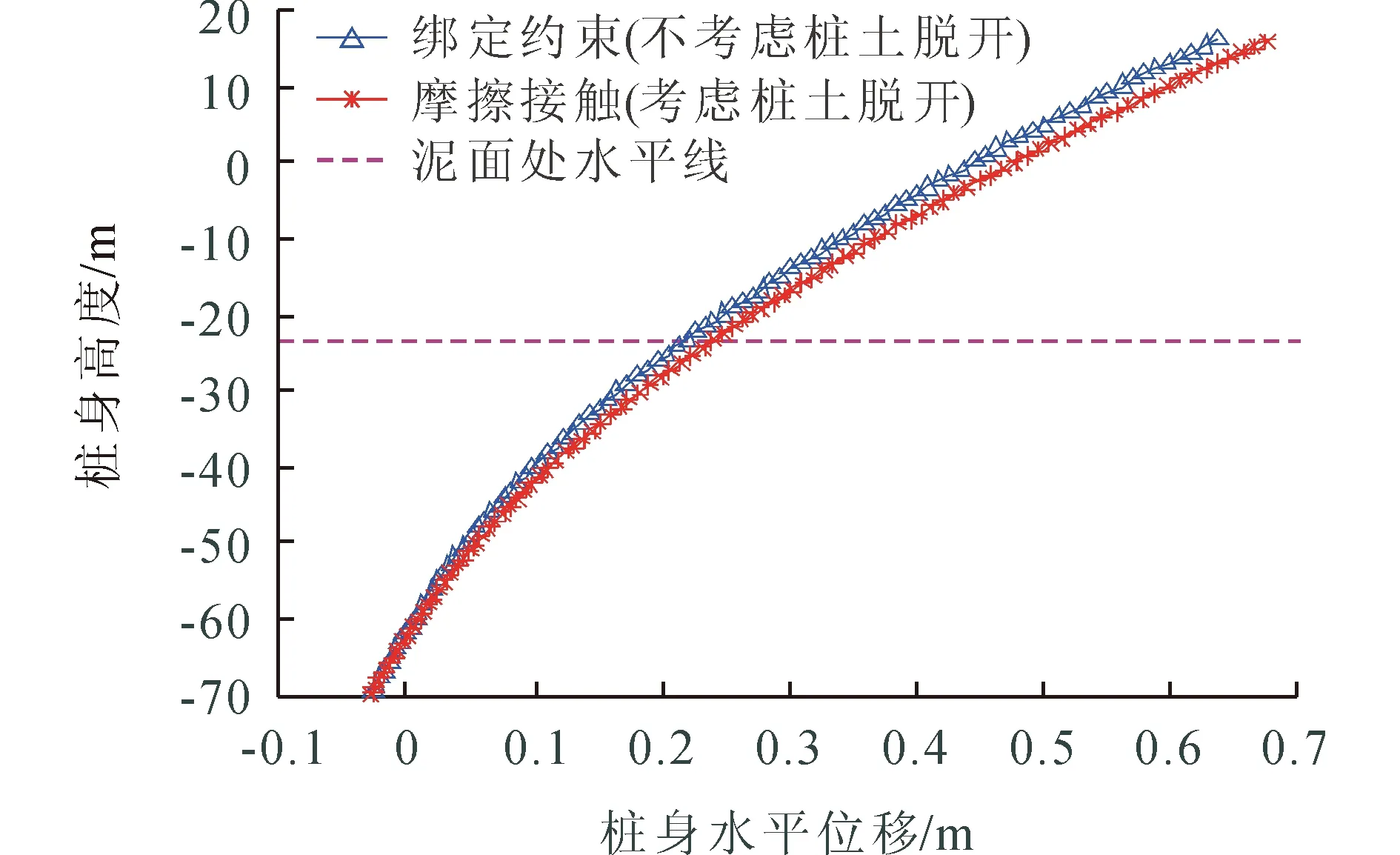
图6 不同桩-土接触面设置下钢管桩水平位移曲线

可以看出，桩-土接触面为摩擦接触的水平位移要大于绑定约束的水平位移，这主要是由于在荷载作用下，桩-土接触面为绑定约束时，土体与桩身未发生脱开，导致桩身变形后仍然与后方土体之间存在相互作用力，从而导致桩身变形位移变小。

4 结 语

本文依托于莆田某海上风电场项目，基于大型有限元软件ABAQUS针对超大直径单桩基础，分别就土体本构关系、土体物理参数(如土体弹性模量、内摩擦角、土体剪胀角)以及桩-土接触模型设置等影响变形计算的因素从静力计算方面展开敏感性分析。从计算分析中可以看出土体弹性模量为影响桩体泥面位移的关键因素，土体本构关系次之，而内摩擦角、剪胀角等由于本机位地层的淤泥层较厚影响不大，以上分析结果也可为后继工程单桩基础的设计计算作为参考。