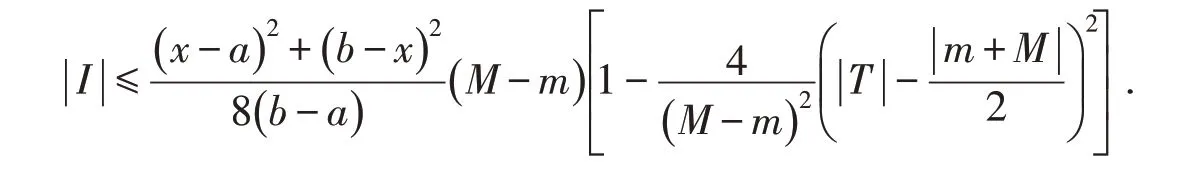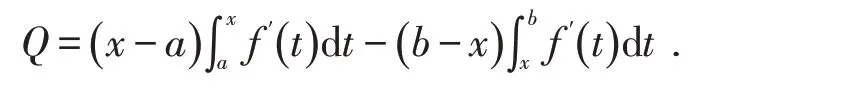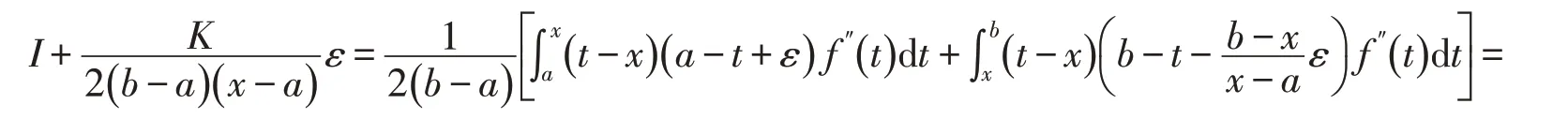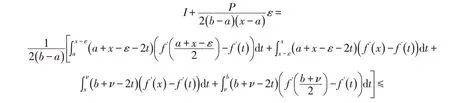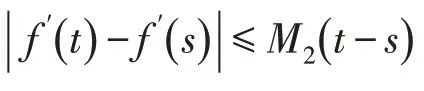一个Ostrowski-Grüss型不等式的加强和推广
2022-01-11曾志红时统业张然然
曾志红,时统业,张然然
(1.广东第二师范学院 学报编辑部,广东 广州 510303;2.海军指挥学院,江苏 南京 211800;3.广东第二师范学院 数学学院,广东 广州 510303)
1 引言和引理
1938年,Ostrowski[1]利用一阶导数的界给出函数在区间上的平均值与其在区间上任意点处的函数值之差的估计.


关于Ostrowski型不等式这里推荐文献[2-9].为方便起见,引入下面记号:


引理1[6]设f:[a,b]→R是可微函数,且f′在[a,b]上可积,x∈[a,b],则有
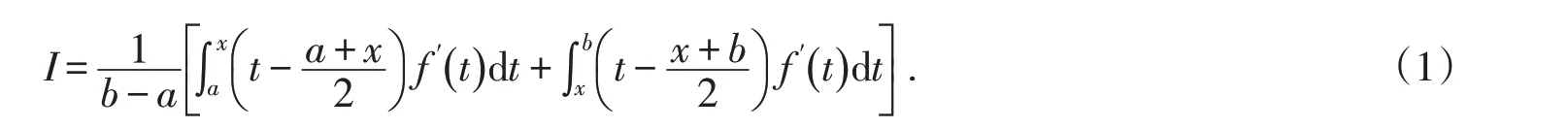
文献[6]利用式(1)得到定理2.
定理2[6]设f:[a,b]→R是可微函数,且f′在[a,b]上可积,存在常数m和M,m 文献[11]将式(3)作了推广. 定理4[11]设f在[a,b]上可导,且f′在[a,b]上可积,并且在[a,b]上满足m≤f′≤M,则有 本文在一阶导数有界或者函数满足Lipschitz条件的情况下建立不等式,给出了式(2)的加强,同时也是Iyengar不等式的推广.针对二阶导函数有界的函数,文献[9]得到一类Ostrowski型双边不等式.本文还将在二阶导数有界的情况下建立新的不等式,我们需要下面的引理: 证明当x=a时,式(5)即式(4),由定理4知结论成立.下面假设x∈(a,b].利用分部积分法得 以下证明同定理5,这里略去. 推论1设条件同定理6,则对任意x∈[a,b]有 证明当x=a时,式(7)即式(4),由定理4知结论成立.下面假设x∈(a,b].利用分部积分法得 定理8设条件同定理5,则对任意x∈[a,b]有式(7)成立. 以下的证明同定理7,这里略去. 推论2设条件同定理5,则对任意x∈[a,b]有 定理9设f:[a,b]→R二阶可微,且f″在[a,b]上可积,存在常数m2和M2,m2 t≤M2,则对任意x∈[a,b],有 证明利用分部积分法得 当x∈(a,b]时,对任意常数ε∈[0,x-a],利用引理2得 在式(11)中取ε=ε3,则式(9)的右边不等式得证. 当x=a时,对任意常数ε∈[a-b,0]有 以下证明类似于定理9略去. 在式(16)中取ε=ε5,则式(14)的右边不等式得证. 当x=a时,对任意常数ε∈[a-b,0]有 定理12设条件同定理10,则对任意x∈[a,b],有式(14)成立. 证明当x∈(a,b]时,对任意常数ε∈[0,x-a],有 以下证明类似于定理11,这里略去.
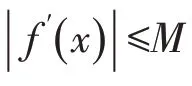
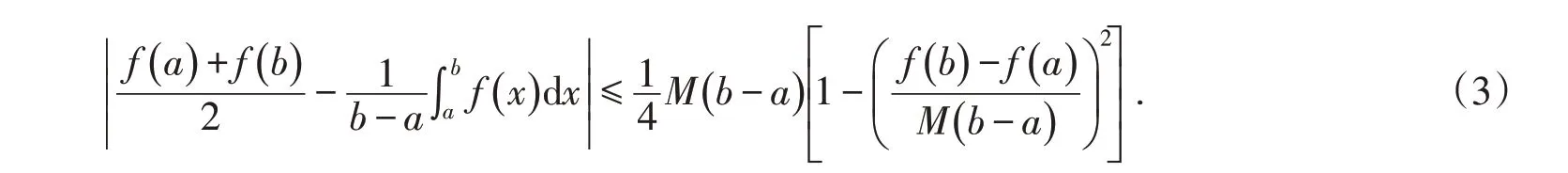


2 主要结果