Prognosis of Gas Turbine Engines Using Ensemble Dual Particle Filters

2022-01-11JingYangKhashayarKhorasaniYingqingGuo

风机技术 2021年6期

Jing Yang Khashayar Khorasani Ying-qing Guo

（1.School of Power and Energy,Northwestern Polytechnical University,Xi’an,Shaanxi,China.2.Department of Electrical and Computer Engineering,Concordia University,Montreal,Quebec,Canada.)

Abstract：A problem of interest to aircraft maintainers is automatic detection,classification,and prognosis of potential critical component failures in the gas turbine engines.Automatic monitoring offers the promise of substantially reducing the cost of repair and replacement of defective parts and may even result in saving lives.In this paper,an integration architecture is proposed for gas turbine engine prognosis through utilization of dual particle filters and ensemble learning methods.In our proposed framework,dual particle filters are utilized to estimate the states as well as the health parameters of the gas turbine engine system.An Long-short term memory neural network based observation forecasting scheme is developed to extend the system observation profiles to future time horizon.Moreover,we develop multiple predictors,each with differing properties so that multiple estimates can be made based on different possible scenarios.A data fusion architecture is presented that combines multiple prognostic techniques weighted by their individual prediction uncertainty for the remaining useful life(RUL)of a gas turbine engine asset.The architecture is based on the concept of ensemble learning method.To verify and validate the above results and as a case study,our proposed ensemble approach is applied to predict the health condition of a dual spool jet engine.The developed ensemble architecture provides improved decision support in comparison to the existing single prognostic technique methods that are available in the literature.

Keywords：Prognosis;GasTurbine Engine; Particle Filter; Ensemble Learning

Nomenclature

mass flow rate

CCcombustion chamber

HChigh-pressure compressor

LClow-pressure compressor

HThigh-pressure turbine pressure

LTlow-pressure turbine

N1,N2rotational speeds

Vvolume

ηefficiencies

θfault vector

0 Introduction

The process of performing operational action based on the information available from the equipment and its interacting environment is termed Equipment Health Management(EHM).Advantages such as lowering sustainment costs and improving maintenance decision making are significant motivations to enhance EHM capabilities.Asset health prognosis(prediction of future health states) has an important role in providing informed EHM.Effective prognosis demands projection of the estimated health state forward in time to produce a bounded estimate for when the component health crosses a preset threshold at which it can no longer perform its function to the satisfaction of the requirements.The time remaining before this threshold is reached is termed as the remaining useful life (RUL) of a component or system,which is generated and estimated from predictive models of the future health state.

Linear and Gaussian models that are developed to achieve satisfactory performance in diagnosis and prognosis applications utilize lower complicated representations of the actual nonlinear dynamic models.Although these models may have acceptable performance for short-term interval applications,as the prediction horizon extends to include longterm behavior of the system,such as the case in the prognosis application,the linear models would not necessarily lead to an accurate solution.Therefore,development of innovative model-based algorithms must be investigated that can satisfy the prediction requirements for both short-term and long-term behaviors of the system.

Particle Filters(PF)is one of the most popular recursive nonlinear state estimation methods that addresses the Bayesian recursive relations using Sequential Monte Carlo (SMC)methods.SMC methods represent as a set of simulationbased techniques that provide an interesting approach to compute the states posterior distributions so that statistical estimates can be easily computed.In the work of Daroogheh et al.(2018a),nonlinear Bayesian and Sequential Monte-Carlo(SMC) methods are applied to develop a consistent framework for both state and parameter estimation objectives for fault diagnosis and prognosis problem of a gas turbine engine system.

For the long-term prediction of the system states and health parameters as required in the dual particle filter-based prognosis framework,an adaptive scheme for observation profile forecasting is proposed in Daroogheh et al.(2018b).In this work,a Long-Short Term Memory (LSTM) based recurrent neural network (RNN) is developed and applied.RNN is a network having internal loops allowing information to persist.Moreover,RNNs using LSTM units solve the vanishing gradient problem,since the LSTM units allow gradients to also flow unchanged,as mentioned in Greff et al.(2017).

However,due to the influence of the system,environmental noise,among others,the system is subject to strong uncertainty,which will make predictions less accurate.Therefore,the ensemble learning method is used to solve this problem.Ensemble methods use multiple learning algorithms to obtain an improved predictive performance than that could be obtained by any of the constituent learning algorithms alone,as has been applied in fault prognosis in van Heeswijk et al.(2009),Zuo et al.(2010),and Lim et al.(2017).In this work,we apply this methodology to ensemble regression to further improve the prediction stability of the particle filters.To construct the ensemble model presented in this paper,a number of Dual Particle Filters (DPF) of varying process noise are generated,each of which is individually trained on the data.After training,these individual models are combined in an ensemble model to achieve our final prognosis strategy.

1 Fault Prognosis of a Gas Turbine Engine

In this paper,our proposed prediction framework is applied to the problem of the prognosis of a nonlinear model of a dual spool gas turbine engine.The details of the model are briefly included below for sake of reader convenience.

1.1 Model Overview

Based on the available literature in Camporeale et al.(2006) on modeling of aircraft jet engines,a Matlab Simulink model for a dual spool engine is developed.Rotor and volume dynamics are considered in order to obtain a nonlinear dynamics for the system.In order to take into account the volume dynamics,the engine components are considered to model an imbalance mass flow rate.This results in elimination of large algebraic loops in the model.The detailed mathematical expressions corresponding to the overall engine dynamics as well as each specific component are developed and presented in the literature as in Meskin,Naderi,and Khorasani (2013).A schematic depicting the main modules and the overall information flows and interdependencies that are present in the gas turbine engine is shown in Fig.1.The states,health parameters and the output measurements in the dual-spool jet engine are selected as

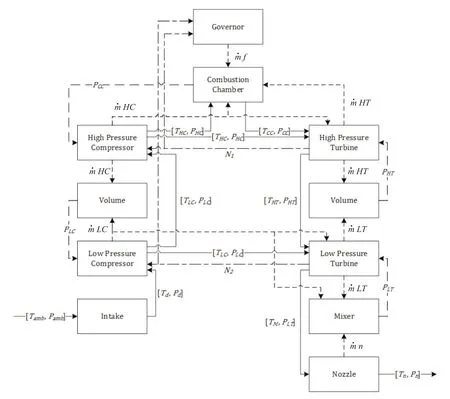
Fig.1 The aircraft jet engine modules and information flowchart and interdependencies.

1.2 Simulation Scenarios

Two scenarios,namely fouling and erosion,are chosen to verify the proposed methodology and algorithm.As stated in Li and Nilkitsaranont(2009),the critical values for the parameter degradations are considered to be a 3% decrease in the compressor efficiencyalong with a 1.5% decrease in the mass flow capacitydue to the fouling phenomenon.This implies that after achieving this level of deficiency in any of these parameters,the compressor must be taken for maintenance and wash-up.On the other hand,the critical values for detecting erosion in the gas turbine are considered to be a 6% decrease in the turbine efficiencyand a 3% increase in the mass flow capacity.The output measurements associated with these two scenarios are shown in Fig.2.

2 Problem Statement and Dual Particle Filters

In model-based prognosis and health monitoring approaches,the first step in formulating the problem is to characterize the damage model.Let us consider the following nonlinear dynamical system,

whereis the system state,is a known differentiable function that determines the relationship between the health parameters and the system states,θt∈is an unknown and possibly time-varying multiplicative fault vector that represents the damage effects on the system health parameters (for the healthy systemθtis set to 1),yt∈is the output measurement,ωtandvtare uncorrelated noise sequences with covariance matricesWtandVt,and mean valuesμωandμv,respectively(although without loss of generality the meanμv≡0 subsequently),φt:×R×andγt:×R×are known nonlinear functions representing the relationship between the states,parameters and the output measurements (observations).The degradation phenomenon in mechanical systems can,in general,be identified from the changes it causes on the efficiency of the system,where the efficiency is designated as the health parameter that can be analytically obtained from the states and measurements of the system.The process noise is not considered as an additive noise since corresponding to our main focused application problem(that is,a mechanical aircraft gas turbine engine system) the additive process noise assumption is not necessarily valid.

A brief background corresponding to the dual state and parameter estimation algorithm,as has been developed in Daroogheh et al.(2013),is now presented in this section.In the developed dual state and parameter estimation structure two concurrent filters are implemented for the state and parameter estimation tasks.At each time step for the state (parameter) estimator filter,the parameters (states) are treated as being known inputs to the filter from the parameter (state) estimator.Our main goal in the dual state and parameter estimation problem is to approximate the following conditional expectations,

wherey1:t=(y1,y2,…,yt)denotes the available observations up to the time instantt,are functions of states and parameters,respectively,that are to be estimated. The conditional probability functionsare to be approximated by the designed particle filters(PFs) through determining the filtering distributions according to,

3 Prediction Framework

Fig.3 provides the main idea for the ensemble learning based fault prognostic method.At first,applying the DPF to future time instants where the weight update in the long-term prediction using particle filters cannot be easily implemented in absence of future observations.Long-short term memory network is a special kind of RNN,capable of learning longterm dependencies.Then,multiple DPFs can be applied to evalute the states and health parameters.Finally,by performing ensemble on prediction results of multiple models,a final more accurate prediction result can be obtained.

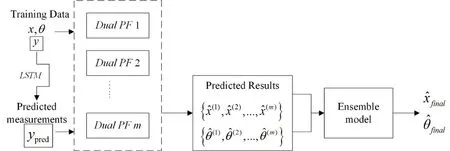
Fig.3 Ensemble regression by combining different dual particle filters.

3.1 Observation Forecasting with Long-Short Term Memory(LSTM)Networks

LSTMs are explicitly designed to avoid the long-term dependency problem and proposed by Hochreiter and Schmidhuber (1997).Restoring information for long periods of time is practically the default behavior and not challenging to learn.All recurrent neural networks have the form of a chain of repeating modules.In standard RNNs,this repeating module will have a very simple structure,such as a single tanh layer.As Fig.4 shows the LSTMs also have this chainlike structure,but the repeating module has a different structure.Instead of having a single neural network layer,there are four,interacting in a very special way.

Fig.4 Recurrent neural network and LSTM cell.

The key to LSTMs is the cell statect.The cell state at time steptis given by

whereftis the forget gate,itis the input gate,gtis a cell candidate as given in Table 1.⊙denotes the Hadamard product (element-wise multiplication of vectors).The LSTM cell uses the hyperbolic tangent function (tanh) to compute the state activation function and uses the sigmoid function given byσ(μ)=(1 +e-μ)-1to compute the gate activation function.

Tab.1 Inner Gates of a Long-Short Term Memory(LSTM)Cells

The hidden state at the time steptis given by

Consequently,an LSTM layer withytas input andhtas output can be constructed.In order to achieve prediction of the measurementsyt,a regression network ℒ is needed to be constructed as follows

whereandytare vectors with lengthny.

The network ℒ is composed of two layers.The first layer is the LSTM layer to obtain the hidden outputht,and the second layer is the fully connected layer to obtain the output.The fully connected layer is applied as,

In order to achieve the predictive capability of the regression network ℒ,the network ℒ is trained to minimize the following loss function,which represents the half-meansquared-error of the predicted responses corresponding to each time step

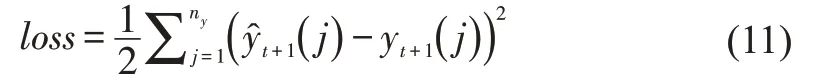
One step ahead prediction results are shown in Fig.5,where the network ℒ is trained with 500 points of degradation process data using the LSTM network.First 100 pointsyare evaluated by the true observed datayt,then the following 400 pointsyare predicted by the predicted.Three solvers to deal with loss function are tested,which are SGDM (Stochastic Gradient Descent with Momentum),ADAM (adaptive moment estimation),introduced in Kingma and Lei Ba(2015),and RMSprop(root mean square propagation),introduced by Wang and Manning(2013).

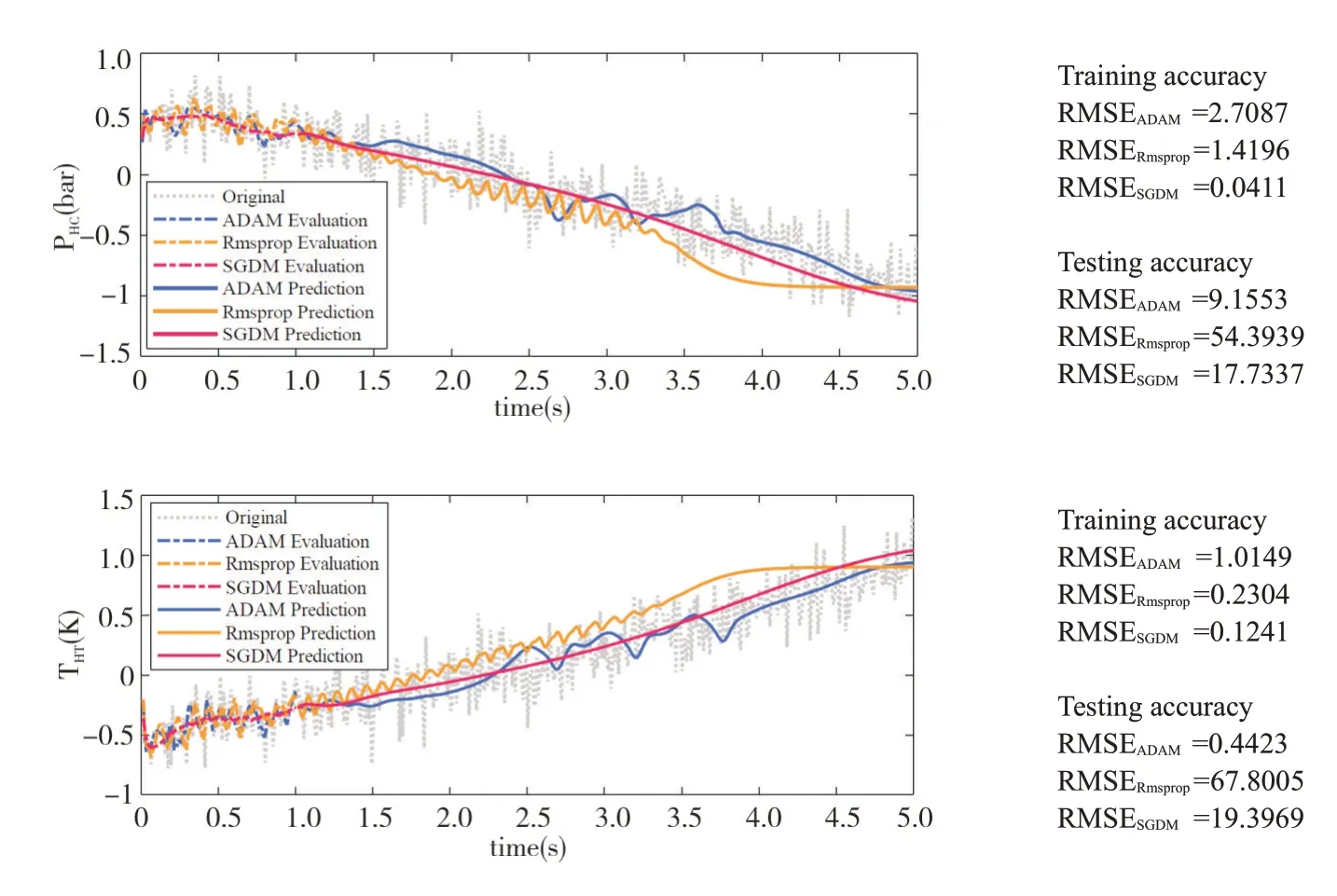
Fig.5 Evaluation and prediction results of the normilized state parameter using the LSTM network and various solvers.

As shown in Fig.4,the SGDM has the best training accuracy.However,the ADAM has the best testing accuracy,meanwhile its training accuracy is also good.Therefore,for this case study the ADAM is applied as the solver method for the LSTM training.

3.2 States and Health Parameters Prediction using Dual Particle Filter and LSTM Network

When performing predictions,the system state functionφand the observation functionγare assumed to be known.In addition,the measurements decay process foryhas been initiated.Therefore,one can construct the degredation model ofyfrom past measurements.

State and parameters can be estimated as described in detail in Daroogheh et al.(2018b),according to the designed dual particle filters(DPF).Specifically,we have

In this part,ytuses the prediction result of the LSTM networkL,that is,yt=L(yt-1).

The details corresponding to states and parameters predictions procedures (DPF) are provided and summarized below.Specifically,

1) Perform the one step aheada prioristate prediction as follows:

b) Calculate the first step a posteriori parameter estimation distribution,

c)Resampling to approximate a posteriori parameter estimate distribution,

d)Obtain the posteriori parameter estimate:

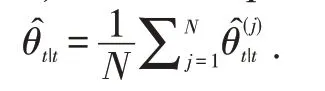
3.3 Ensemble Dual Particle Filter And Fault Prognosis

Ensemble learning explores the diversity of models and fuses the results from different models.The proposed ensemble DPF consists of two stages.In the first stage,mdifferent DPF models are constructed from knownx,θandyto obtain a set of prediction resultsand.In the second step,the prediction results are integrated to obtain the final prediction result

From the DPF calculation method introduced in the previous section,it can be seen thatωtin(13)is a changing factor in the DPF calculation process,and the noise of the system environment can affect the estimation process.Meanwhile,vtin(2)did not appear during the calculation of DPF.Therefore,in the first step of ensemble DPF,we obtain different models by modifying the process noiseωtin (1) of the DPF,whereωtis computed from

whererandn is a Normally distributed random numbers,δωis the weight coefficient.The experimental results ofδωchanges from 0.02 to 0.05 are given in Fig.6,and five tests are performed under each data.It can be seen that by changingδω,the distribution of the predicted data has changed.

Fig.6 Predicted states of diverse dual particle filters(the number of particles is 200).

Therefore,the ensembled predicted state (or health parameters)are obtained from the results,j=1,…,Ncorresponding to different models according to

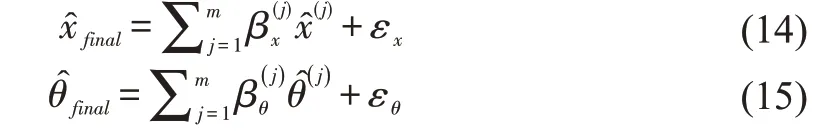
The specific computational procedure of parametersβx,βθ,εx,εθis described in the next section.

To calculate the system RUL when multiple health parameters are estimated,we first denote and selectθcras the critical value for the health parameters.The following rule is now utilized for evaluating the RUL at timet,namely:RUL(t)=tj-t,wheretjis the time at which the first parameter associated with the specific degradation damage reaches its critical value.Once reaching the critical value in one of the parameters,maintenance must be performed.Choosing the suitable value forθcris application specific and is generally determined based on the system performance and operator experience.In most applications and problems defining an exact value for the RUL is not possible.Therefore,an acceptable bound is considered as a confidence interval for the RUL prediction.The above procedure is used for estimating the RUL for a k-step ahead horizon before the occurrence of a failure.

3.4 Simulation Results of the Ensemble DPF

We have tested three methods for performing the ensemble operation,namely the Robust Linear Regression (RR),the Multivariate Normal Regression (MNR),and the mean value(average).

Fig.7 Predicted error of state N1 (bar)and health parameter using different stacked regression methods(fouling phenomenon).

Fig.8 Predicted error of state PLC (bar)and health parameter using different stacked regression methods(fouling phenomenon).

By using the mean value method,the parameters in(14)-(15)are simply set intoε=0,βj=1/m.The linear regression is based on certain assumptions,such as a normal distribution of errors in the observed responses.If the distribution of errors is asymmetric or prone to outliers,model assumptions are invalidated and parameter estimates confidence intervals,and other computed statistics become unreliable.We use robust regression to create a model that is not much affected by outliers.The robust fitting method is less sensitive than ordinary least squares to large changes in small parts of the data.

Robust regression works by assigning a weight to each data point.Weighting is done automatically and iteratively using a process called iteratively reweighted least squares.In the first iteration,each point is assigned equal weight and model coefficients are estimated using ordinary least squares.At subsequent iterations,weights are recomputed so that points farther from model predictions in the previous iteration are given a lower weight.Model coefficients are recomputed using weighted least squares.The process continues until the values of the coefficient estimates converge within a specified tolerance.

Multivariate normal regression is the regression of addimensional response on a design matrix of predictor variables,with normally distributed errors.The errors can be heteroscedastic and correlated.Applied here can be considered as a missing partial response mission.

As shown in Fig.s 7 and 8,ensemble regression can reduce the maximum residuals of the multiple single estimations.In the proposed three ensemble regression methods,the MNR method has the lowest predictor error than the other two methods.

Since RUL calculate the predicted values based on health parameters,the smaller the residual between the predicted values and the true values,the more accurate the RUL predictions will be.The difference between the health parameters and the actual values MNR the three integrated algorithms proposed in this paper is the smallest,so it can be seen that the prediction of the RUL is also the most accurate.

4 Conclusions

In this paper,a novel ensembled estimation filtering scheme is proposed and developed based on dual particle filters(DPF),LSTM and ensemble learning methods for a dual spool gas turbine engine.Long-short term memory (LSTM)network is applied to forecast measurements that yielded an ideal prediction effect.States and health parameters are estimated by utilizing dual particle filter,which is corrected with the predicted measurements from the LSTM.Moreover,the multiple estimation results(states and health parameters)that are obtained by changing the process noise are further optimized by an ensemble mechanism.Simulation results show that the proposed ensemble DPF method can improve the stability of fault prognosis scheme by balancing different conditions.