顾及自身吸引力的公园时空可达性与变化强度分析

王 俊, 李 斌, 张焕雪, 邢汉发,2,3,4*, 曹端广

(1. 山东师范大学地理与环境学院， 济南 250300; 2. 华南师范大学地理科学学院， 广州 510631;3. 华南师大(清远)科技创新研究院有限公司， 清远 511517; 4. 广东师大维智信息科技有限公司， 清远 511517;5. 山东建筑大学测绘地理信息学院， 济南 250101)

城市公园是城市生态系统和城市景观的重要组成部分[1]，是城市居民休闲、娱乐的重要场所，是表示城市整体环境水平和居民生活质量的一项重要指标[2]. 随着社会经济的快速发展和人民生活水平的提高，城市居民对于城市公园活动休闲的需求与日俱增，居民不仅关注公园的数量和质量，更关心其所提供的自然服务能否被便捷、公平地享用[3-4]. 城市公园的可达性是衡量公园服务功能的有力指标[5]，如何客观真实地评价城市公园的可达性是学者们长期关注的问题.

可达性指从出发点到达目的地过程所克服的空间阻力大小，通常用距离、时间和费用等指标来衡量[6-7]. 目前，可达性评价的主要方法有最小距离法[8]、缓冲区分析法[9]、网络分析法[10]和引力势能模型法[11](引力模型法[12]、两步移动搜索法[13])等. 其中，由于人口分布、时间变化和公园自身吸引力等对可达性的影响因素未被考虑，最小距离法对反映某一地区的真实可达性很难做到全面客观；由于未考虑公园自身吸引力以及道路网络对居民出行的影响，缓冲区分析法对可达性的量化结果存在一定误差；网络分析法顾及了道路网络对居民出行的影响，但是仍然缺乏对公园自身吸引力的评价；引力模型法从城市公园的吸引力[14]、道路网距离衰减效应[15]和人口势能[16]等方面系统地对公园广场做出的评价则相对客观合理. 如：董小刚等[17]基于改进的引力模型，在考虑广场公园规模与人口规模影响因子的情况下，更加客观真实地评价广场公园的可达性；FAN等[18]开展了一项专家调查以确定可达性与公园质量的相对重要性，但该类通过专家调查评价的研究方法并没有形成统一的评价标准，调查的方式也费时费力. 城市公园自身吸引力受多种评价指标影响，因此，建立公园吸引力评价模型将有利于促进可达性研究更加全面真实地反映现实状况. 此外，城市公园可达性受交通状况影响，在时间上是动态变化的. 黄应淮等[19]利用高德地图获取了最短通行时间，结合微信热度数据进行城市公园可达性分析，但是忽略了可达性在空间上是整体稳定的、在时间上却是动态变化的特点；LI等[20]提出了一种基于浮动车实时行驶速度的动态可达性度量方法；MOYA-GMEZ等[21]提出利用推特(Twitter)数据，采用动态的方法分析城市可达性，该研究考虑到了可达性的动态特征. 但是，上述研究所采用的相关数据均不公开，使得可达性的研究极大地受限于数据获取问题.

针对以往公园可达性研究中存在的未考虑公园自身吸引力以及缺乏动态特征方面的不足，本文提出了一种顾及公园自身吸引力的城市公园时空可达性研究方法(Spatial-Temporal Accessibility of Attraction-Oriented Urban Parks,STAAOP)：首先，基于众源地理信息数据，采用熵权法[22]构建公园吸引力评价模型，为可达性研究提供真实可靠的吸引力评价指标；然后，在道路匹配的基础上，借助百度地图应用程序接口提取实际道路状况和导航数据，进而得到路网动态信息，实现对城市公园可达性动态特征的研究. 采用STAAOP方法，对济南市主城区城市公园可达性进行评价分析，以期能够丰富城市公园可达性评价体系，为更准确、真实评价城市公园动态可达性提供一种新的思路.

1 研究区及数据来源

1.1 研究区概况

研究区域为山东省济南市中心城区(36°32′12′′N～36°46′26′′N，116°51′19′′E～117°07′37′′E)，占地535 km2，地处泰山山脉北部与黄河以南，经十路横贯研究区将其一分为二(图1). 该城市人文积淀深厚，历史悠久，经济发展水平和人口密度均相对较高，公园绿地资源丰富，拥有包含森林公园、综合公园和社区公园在内的多类型城市公园绿地系统. 同时，济南市交通状况复杂多样，同样适合于城市公园可达性的研究.

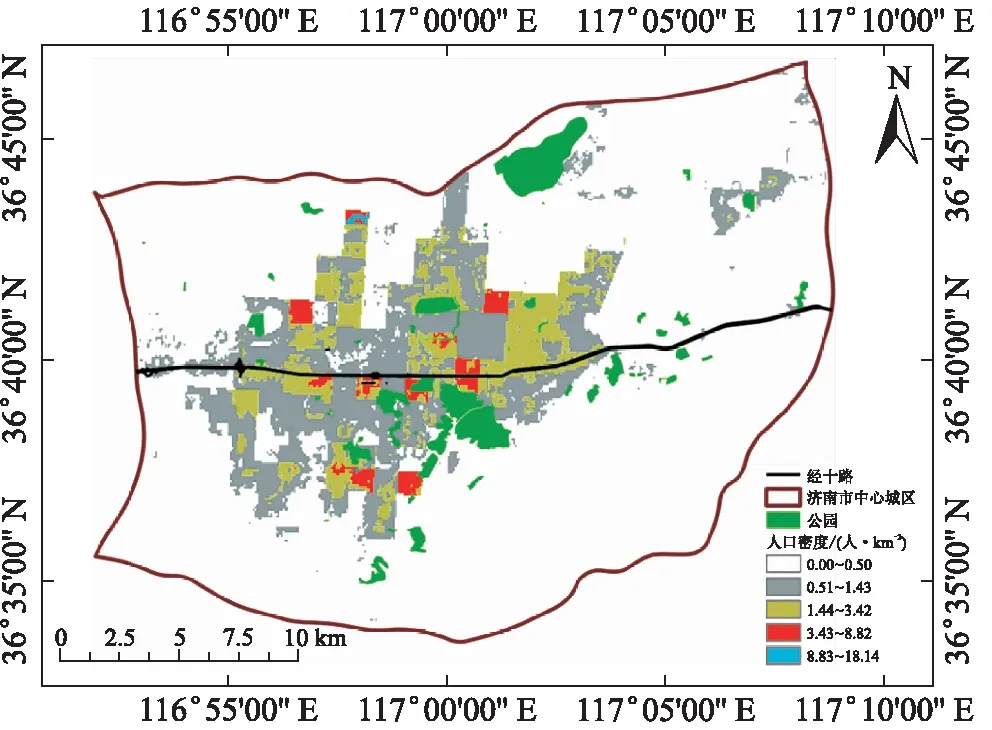
图1 研究区概况

1.2 数据来源

实验数据集包括2020年最新行政区划、公园、人口、道路以及高德地图2020年11月的时间序列实时导航数据，其中：行政区划数据来自国家基础地理信息中心；公园数据是利用网络电子地图，通过网络爬取以及补充数字化而得到的；人口栅格数据为2020 年济南市100 m分辨率人口栅格数据，下载于World-Pop网站(http:∥www.worldpop.org/)；路网数据通过OpenStreetMap(https:∥www.openstreetmap.org/)获得；时间序列实时导航数据是使用百度地图API(Application Programming Interface)提供的路径规划接口来获取的实时的出行时间，并且积累一整个月的数据以求得平均出行时间.

本文通过百度地图API收集了步行、骑行和私家车3种模式的出行时间. 百度地图API返回的出行时间可自行选择出行方式，同时将基于百度地图大数据的交通拥堵情况和百度地图API返回的出行时间相结合，使得结果更加客观可靠. 本文以OSM道路网划分了1 068个街区，以街道的几何重心为起点、以公园的导航坐标为终点、以3小时为时间间隔来获取导航数据，并且使用平均出行时间来避免极端天气、重大交通事故和交通管制等意外情况，以充分说明出行的时间成本. 本文共下载一个月数据，用于获取平均出行时间，计算公式如下:

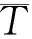
2 研究方法

本文提出的STAAOP方法的具体步骤为：首先，基于众源地理数据，采用熵权法构建公园吸引力评价模型，评价结果作为输入参数1；然后，利用电子地图开源API，以3个小时为时间间隔爬取实时导航数据，作为输入参数2；其次，基于两步移动搜索法(Two Step Floating Catchment Area，2SFCA)[23]构建公园动态可达性度量模型；最后，计算可达性变化结果的标准差，运用局部空间自相关分析法识别可达性变化的聚类区域与异常区域，从整体和典型区域的角度分析可达性的变化强度(图2).

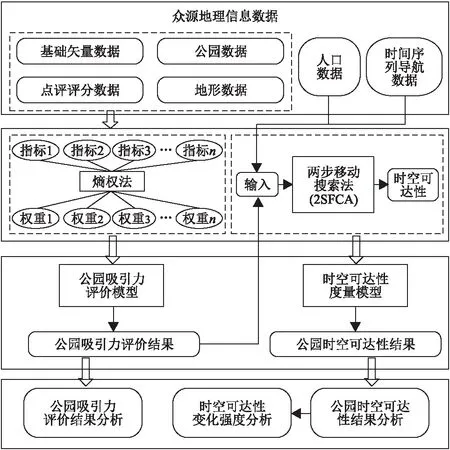
图2 顾及公园自身吸引力的城市公园时空可达性研究方法

2.1 基于熵权法的公园吸引力评价

本文利用众源地理数据构建公园吸引力评价指标体系，将供应点自身吸引力纳入可达性度量模型中，基于熵权法对公园吸引力进行评价. 熵权法的基本思想是根据指标变异性的大小确定客观权重，评价指标及其权重结果如表1所示，其中：描述地理位置与环境的地形起伏度为该地区最大高程与最小高程之差；分布均匀度为描述公园相对位置的指标，其计算公式如下：

表1 公园吸引力评价指标体系Table 1 The index system of park attraction evaluation

其中，S为公园个数，Pi为某类公园数占总公园数比例.

熵权法基本流程如下所示：

(1)数据标准化. 采用极值标准化的方法，由于均为正向指标，故计算公式如下：

其中，xi为第i个指标的数值集合，max(xi)、min(xi)分别为xi中的最大值、最小值，xij为第i个指标的第j个样本，Yij为标准化后的值.

(2)计算各指标的信息熵. 为解决对信息的量化度量问题，利用熵权法，通过引入信息论中信息熵的概念来描述信源的不确定度. 一组数据的信息熵的计算公式如下：

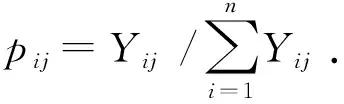
(3)确定各评价指标权重. 计算公式如下:

其中，Wi(i=1,2,…,k)为第i个指标的权重.

2.2 基于两步移动搜索法的动态可达性度量

其中,dij为需求点i和供给点j间的距离,Rj为供给点j的设施规模与搜寻半径(d0)内所服务的人口的比例,Sj为供给点j的供给规模,Dk为需求点k的需求规模.

本文具体计算方法如下：

第一步：设每个公园的质心点为j，以时间阈值为半径建立搜索域，搜索所有在质心点j的时间阈值范围内的街区地块质心，计算搜索范围内的人口密度，从而得到供需比Rj(即每个公园的服务能力)：

其中，Sj为公园的吸引力评价分数，tkj为从质心点j的时间阈值范围内的街区地块质心k到达点j的时间，Dk为搜索范围内的人口密度，t0为公园到所有街区地块的平均时间.

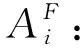
其中，Rj为搜索域街区地块i(tij≤t0)内公园j的供需比，t0为街区地块到所有公园的平均时间.

基于此方法，可得到以3个小时为时间间隔，在步行、骑行、私家车出行状态下的每个街区地块的可达性，将三者相加,从而得到街区地块总可达性.

2.3 基于局部空间自相关分析法的相对变化强度识别

为了识别区域可达性的动态变化程度，较好地识别一天内可达性变化明显的区域，本文选用标准差来衡量可达性的动态变化，继而运用局部空间自相关分析法识别可达性变化的聚类区域与异常区域.

标准差是方差的算术平方根，是反映一组数据离散程度最常用的一种量化形式，是用来表示稳定度的重要指标. 计算公式如下：

其中，xi为i时的可达性结果，μ为一天内的平均值，σ为标准差.

空间自相关分析是理论地理学的基本方法之一，主要用来分析空间数据的统计分布规律[24]. 局部空间自相关分析以Local Moran’s I为统计量，是Moran’s I(Global Moran’s I)的分解形式[25]，本文用其来识别地块可达性结果，从而生成聚类区域与变化异常区域. Moran关联聚集图分为4个等级，代表4种不同关联类型：正相关类型代表聚类区域，分别用高-高聚类、低-低聚类表示；负相关类型代表变化异常区域，分别用高-低异常、低-高异常表示.

3 研究结果及分析

3.1 公园吸引力评价结果及分析

为探究地区间公园吸引力差异性，在公园吸引力模型中，评价分数值越大表示吸引力越大. 利用自然间断点法，将公园吸引力评价结果分为极好、较好、一般、较差和极差5个等级，其对应的数值范围分别为[20.85,43.95]、[15.32,20.84]、[11.89,15.31]、[8.03,11.88]和[3.37,8.02]. 总体来看，实验区大型公园大多背靠南部山区而建立，中小型公园在西部分布较少且较为分散，东部公园数量众多但呈集聚状，实验区公园在空间分布上呈明显不均匀分布. 吸引力等级结果(图3)表明：由于济南市南部地区有着较多天然地表，故经十路中段南侧公园分布数量最多，吸引力等级也整体偏高；其次，城市西部与北部背靠黄河区域中的公园虽然数量较少，但吸引力等级仍然较高；实验区东部的公园分散且整体吸引力处于较低等级.

图3 公园吸引力等级示意图

3.2 公园动态可达性分析

采用自然间断点法，对利用2SFCA方法得到的公园动态可达性度量结果进行分级，共划分为极好、较好、一般、较差和极差5个等级，其对应的数值范围分别是[639.49,1 087.11]、[481.75,639.48]、[315.48,481.74]、[127.90,315.47]和[2.14,127.89]. 由不同时间点的可达性计算结果(图4)可知：研究区域的公园可达性在一天内的动态变化是较为明显的. 济南市区域可达性水平总体呈现中部>西部>东部的空间格局. 变化较为明显的区域为：(1)位置1：工业北路北侧自24时开始，可达性随时间有所下降，12时可达性有所提高，在15时可达性达到最好，随后又有所下降. (2)位置2：腊山住宅区全天可达性变化极为明显，且可达性一般处于“一般”及以下等级，在18时达到最差，整体可达性均为“较差”等级. (3)位置3：燕山立交桥东侧经十路两侧是济南交通状况最为复杂的区域之一，在6时、9时及18时可达性有极其明显的下降，推测主要是由于交通因素所导致. 但由于该区域附近分布有多个吸引力等级较高的公园，所以其整体可达性较好. (4)位置4：领秀城住宅区在3时、6时、15时可达性结果最好，在正常工作日时间，可达性一般处于“较好”等级.

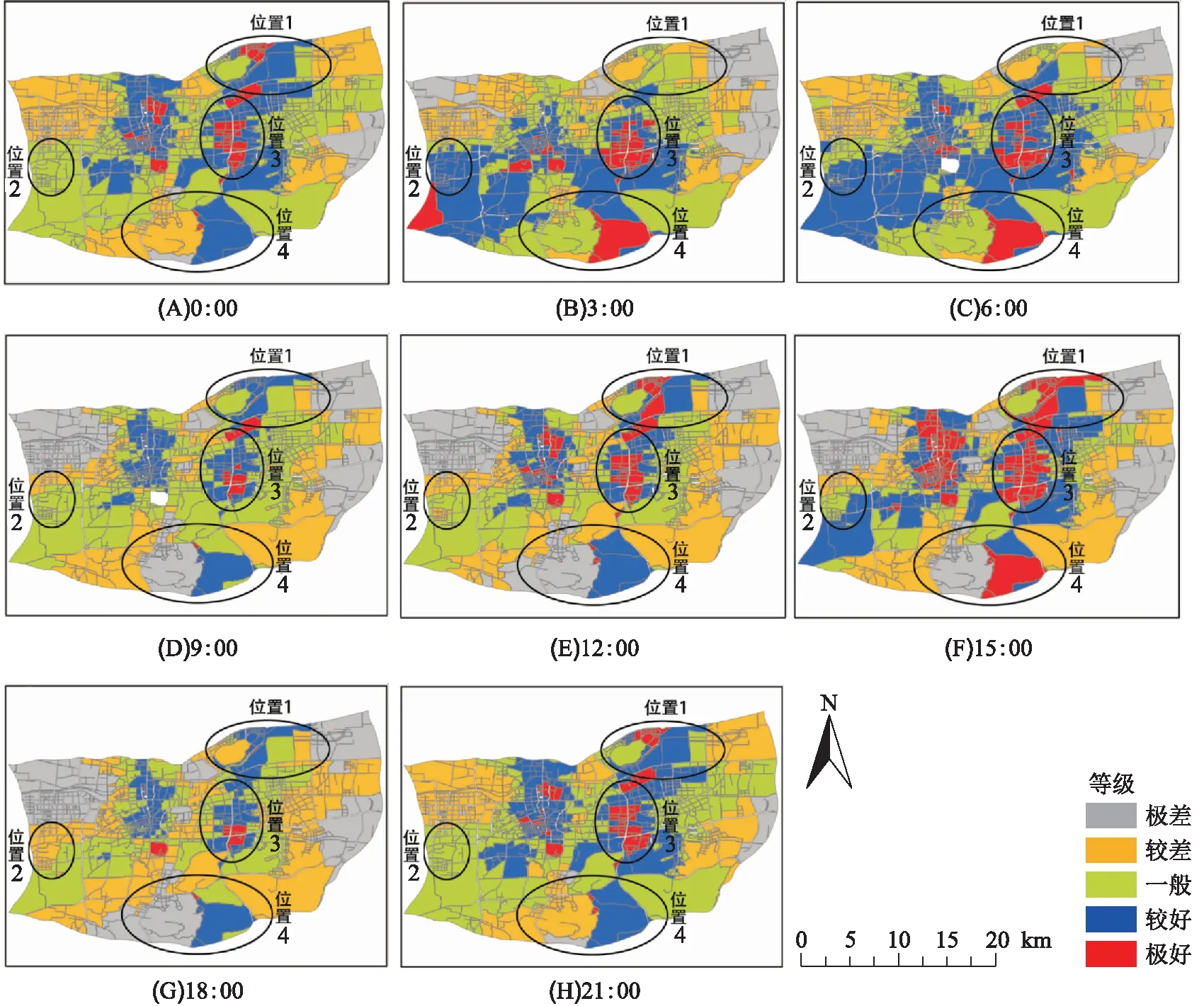
图4 不同时间点的公园可达性计算结果

由不同时间点公园可达性等级占比(图5)可知济南市区公园动态可达性等级在一天内的波动较大：(1)0～9时，多数地块从“较差”及以下等级提升至“一般”及以上等级：0～3时，受到公共交通服务能力的限制，运行的公共汽车、出租车数量明显不足，导致居民出行能力受限，公园可达性等级较低；3时后，出行前往单位及晨练的居民数量增加明显，私家车、非机动车以及公共交通工具数量增加，且该时段道路状况较好，交通繁忙的情况暂未出现，因此，公园可达性等级呈现上升趋势；9时，74%的地块的公园可达性等级在“一般”以上. (2)9～18时，公园可达性水平整体呈下降趋势，18时的“较差”及“极差”地块占总数的57%；9时后，道路情况趋于稳定，运行的公共交通工具及私家车数量较为平稳；15～18时，通勤市民较多，整体可达性达到一天内最低水平；18时后，随着晚高峰的结束，可达性等级有所上升.

图5 不同时间点的公园可达性等级占比

3.3 公园可达性变化强度分析

可达性变化标准差局部空间关联结果如图6所示，其中高-高聚类区域指高值聚类的区域，高-低异常区域指街区周边被低值区域包围的高值区域，低-低聚类区域为低值聚类的区域，低-高异常区域指街区周边被高值区域包围的低值区域. 总体来看：济南市中心城区的公园可达性动态变化强度存在着明显的区域差异，济南市东北部、西南部公园可达性变化强度均较高，存在明显聚类现象. 市外环的公园可达性动态变化强度大，城市内环的较小，且城市公园分布的密集程度并未对城市公园的动态变化强度产生巨大影响. 从各个关联类型角度来看：(1)高-高聚类区域往往位于城市外围人流量波动较大、交通状况相对复杂的公园附近. (2)低-低聚类区域主要集中在经十路两侧，该区域中的城市公园分布密集、可达性变化强度小、公园功能性稳定. (3)高-低异常区域分散在经十路两侧，大多位于交通枢纽、学校和医院等公共设施资源集中区域. (4)低-高异常区域较为稀少，主要位于城区南部部分住宅区，该类区域共同特点是位于交通干线周边，缺少辅助二级道路与支路的区域.

图6 可达性变化标准差的局部空间关联图

4 结论与展望

本文提出了一个顾及供应点的城市公园动态可达性研究方法(STAAOP)：利用熵权法计算公园吸引力评价结果，并将该结果和时间序列实时导航数据作为两步移动搜索法的输入变量，从而构建公园动态可达性度量模型. 以济南市中心城区为实验区的结果表明STAAOP方法在整体和区域识别上都有较好的计算结果：(1)对公园自身吸引力的考虑相对充分，数据要求明显降低，可作为传统可达性研究方法在吸引力分析及时间动态分析的一种改进；(2)能够一定程度上满足城市公园动态可达性定量评价的需求，为更准确、真实评价城市公园可达性提供一种新的思路；(3)研究成果可以在一定程度上服务于济南市城市规划，并为其他地区公园可达性研究提供参考.

本文提出的STAAOP方法仍然有需要改进之处：一方面，本文所构建的公园动态可达性度量模型的可靠性还需要进一步验证，在后续研究中可通过实地统计、大数据辅助等方法进行验证；另一方面，后续还应当区分工作日与非工作日，更加细化24小时内的时间间隔.