基于无人机高光谱影像的植被覆盖度遥感估算模型比较

韦钦桦， 罗文斐， 李 浩， 唐凯丰

(华南师范大学地理科学学院， 广州 510631)

植被覆盖度(Fractional Vegetation Cover，FVC)是指植被垂直投影面积占土地总面积的比例，是衡量地表植被状况的重要指标[1]：表征植被茂密程度、植被质量、植被生长状态和光合作用面积大小的重要参数之一；生物量计算模型、气象数值模型和水文生态模型的重要因子之一；评价生态系统稳定程度的重要指标之一，对保护生态环境起着至关重要的作用[2-5]. 植被覆盖度的应用领域较为广泛，是全球或区域水文、地表植被变化监测、生态等科学研究领域的重要参数和基础数据[6].

可用于估算植被覆盖度的数据源有很多，如：ZRIBI[7]使用雷达数据估算半干旱地区的植被覆盖度；HAN等[8]利用机载LiDAR离散点和强度信息估算南京市多层植被覆盖度；LI等[9]利用Landsat数据估算抚仙湖流域部分地区的植被覆盖度；JIA等[10]使用GF-1(WFV)数据估算中国围场县的植被覆盖度；庞国伟等[11]利用国产GF-1(PMS)数据估算黄土高原典型区的植被覆盖度. 高光谱遥感数据具有较高的光谱分辨率，有着近似连续的地物光谱信息，能够更突出地表现不同地物的光谱特征. 李晓松等[12]利用高光谱遥感数据估算干旱地区的稀疏植被覆盖度，朱蕾等[13]利用高光谱遥感数据估算作物植被覆盖度，ZHANG等[14]利用HJ-1卫星高光谱数据估算新疆石河子地区干旱和半干旱环境中的植被覆盖度，冯海英等[15]基于无人机高光谱遥感数据提出一种估算植被覆盖度的新方法，都取得了较高的植被覆盖度估算精度.

植被覆盖度的估算方法目前主要有2类：回归分析方法和混合像元分解方法. 回归分析方法是利用统计模型构建波段信息(或植被指数)与植被覆盖度之间的关系模型来估算植被覆盖度的方法[16-17]. 这类方法在一定程度上提高了效率、降低了成本，但需大量实测数据为支撑且适用范围较小. 混合像元分解方法是目前最常用的方法，其在某种假定的比例关系下，将混合像元分解为多个纯成份，从而构建像元分解模型[18]. 相比于前者，混合像元分解方法对实测数据依赖小、适用范围广，适合于多种植被类型的植被覆盖度估算且可进行动态监测. 基于混合像元分解理论，学者们提出了不同的解混模型和算法来估算植被覆盖度，如：GUTMAN[19]提出多种植被混合模型估算植被覆盖度；LI等[20]基于改进的可选端元光谱混合模型估算植被覆盖度；李苗苗等[21]利用像元二分模型估算植被覆盖度；闫洋等[22]基于像元二分模型反演新疆天然草原植被覆盖度；刘佳丽等[23]基于像元二分模型对高寒草地的植被覆盖度进行了研究；李晓松等[12]利用全约束混合像元分解方法估算植被覆盖度.

为了比较不同的植被覆盖度估算方法的适应性，学者们对经典的方法进行了对比分析. 如:谢秋霞等[24]对比了回归模型、像元二分模型和混合像元分解法3种方法；董显聪和李晓洁[25]比较了3种经典的混合像元分解模型(像元二分模型、Carlson模型和Baret模型)估算植被覆盖度的适用性. 但在高光谱遥感领域，一些较为成熟且应用广泛的光谱解混模型并没有应用于估算植被覆盖度. 因此，本文利用无人机高光谱遥感数据，比较3种估算植被覆盖度的经典模型(像元二分模型[14]、Carlson模型[26]和Baret模型[27])和3种光谱解混模型(LMM模型[28]、PPNMM模型[29]和NCM模型[30])的估算效果，以期挖掘光谱解混模型的应用潜力，并为植被覆盖度估算的诸多应用提供参考.

1 研究区数据

1.1 研究区数据概况

中山市是广东省辖地级市，位于珠江三角洲中南部，北连广州市，毗邻港澳，年平均温度为22 ℃. 本文的实验区(图1)为中山市民众镇义仓村内一块香蕉林地(113°31′12″E～113°31′18″E，22°36′58″N～22°37′06″N). 实验区内植被分布较为丰富，且含有较为明显的高植被覆盖度区域和低植被覆盖度区域，适用于植被覆盖度估算模型的适用性研究.

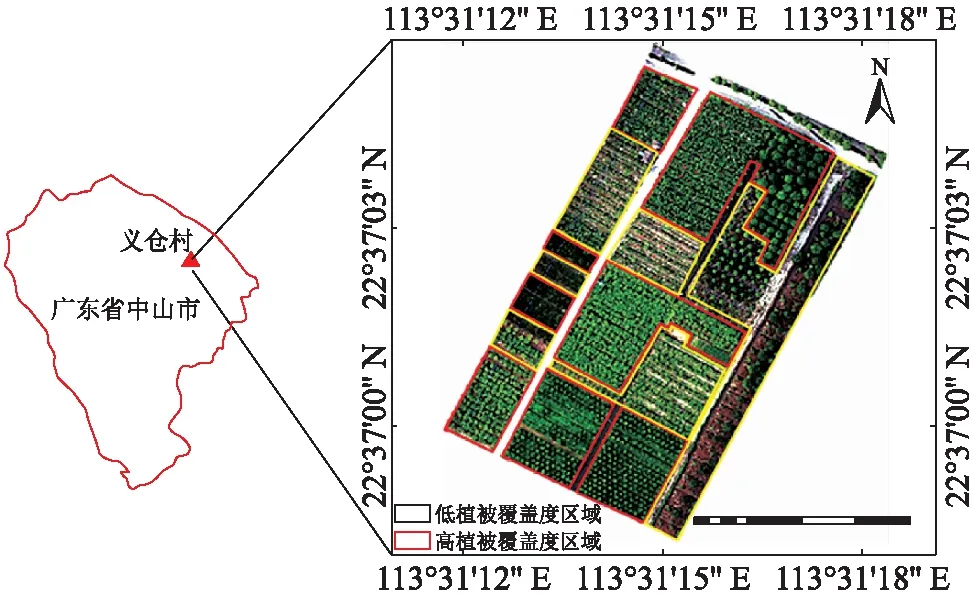
图1 无人机影像实验区域

本研究以无人机高光谱影像为数据源，使用大疆M600pro八旋翼无人机，悬停功耗1 500 W，整机重4.4 kg，有效载荷3 kg. 传感器为美国headwall公司生产的Nano-17mm高光谱相机，共有270个波段，波长范围为401～987 nm. 数据获取时间为2019年7月17日，天气状况良好，无人机拍摄前在影像区域布设了多个地面控制点，方便后期数据的校正工作;在飞行区域放置定标板，用于后期相对定标. 设置无人机飞行高度为400 m，经处理后得到实验用的高光谱影像，该影像幅宽为111.44 m、空间分辨率为17.41 cm.

1.2 数据预处理

数据预处理流程(图2)如下：获取无人机影像后，首先进行相机通道校正，经格式转换后，将波段参数、相机参数和时间参数等整合到无人机影像中，再对该影像进行粗校正；然后，利用定标白板对经过粗校正的影像进行辐射校正，并进一步剔除一些信息缺失、噪声大、质量较差的波段，剔除后的波段为180个有效波段(501～899 nm)；最后，根据影像拍摄前预设的地面控制点进行几何精校正，以获取更准确的无人机影像的相对位置，再利用ROI文件进行掩膜处理，最终选取畸变较小、校正效果较好的区域进行研究.

图2 无人机影像预处理流程图

2 模型与研究方法

2.1 植被覆盖度估算模型

2.1.1 像元二分模型 像元二分模型估算植被覆盖度的基本思想是将一个像元中所包含的信息分为两部分，即植被与非植被[14]. 由像元二分模型的原理可知：一个像元的反射率R可由纯植被像元的反射率(Rveg)与非植被像元的反射率(Rsoil)线性加权表示：

R=f×Rveg+(1-f)×Rsoil，

(1)

其中，f为植被覆盖度.

对式(1)进行推导运算，可得f的表达式：

f=(R-Rsoil)/(Rveg-Rsoil).

(2)

李苗苗等[21]对多个植被指数进行分析，指出以NDVI作为模型参数估算植被覆盖度的精度较高，从而提出了一个修改后的像元二分模型：

FVC=(NDVI-NDVIsoil)/(NDVIveg-NDVIsoil)，

(3)

其中，FVC为影像植被覆盖度，NDVIsoil为非植被覆盖区域的NDVI值，NDVIveg为纯像元植被覆盖区域的NDVI值.

2.1.2 Carlson模型 CARLSON和RIPLEY[26]对描述植被与土壤和大气之间相互作用的辐射传输模型进行研究，提出了根据NDVI估算植被覆盖度的Carlson模型：

(4)

2.1.3 Baret模型 Baret模型[27]的基本原理是通过建立植被覆盖度与植被垂直间隙率之间的关系来估算植被覆盖度. 丁艳玲[31]根据植被指数反演叶面积指数，再结合叶面积指数与垂直间隙率的关系得到改进后的Baret模型：

(5)

其中，Kp是消光系数，与叶倾角、叶片的透过率有关；KVI是模型影响因子，其值取决于植被结构、太阳/观测方向和叶片的光学特性；VIsoil和VIveg分别为非植被和叶面积指数无限大时对应的植被指数值.

2.1.4 LMM模型 光谱解混是从混合像元中提取基本地物和计算各个基本地物在混合像元中所占比例的过程，LMM模型认为混合像元的光谱由若干个基本地物的光谱线性组合而成[28]. 全约束最小二乘法(Fully Constrained Least Squares,FCLS)是一种广泛使用的且较具代表性的LMM模型，其函数表达形式为：

(6)

其中，Y为混合像元光谱，mi为端元，ai为端元丰度，ε为噪声，R为端元总个数.

2.1.5 PPNMM光谱解混模型 相比于线性光谱解混模型，非线性光谱解混模型考虑了地物之间的散射，对混合像元的光谱变化更为敏感，能更准确地提取端元和丰度. 后验多项式非线性混合模型(Poly-nomial Post-nonliner Mixing Model,PPNMM)[29]是目前较为常用的非线性光谱解混模型，其函数形式为：

(7)

其中，Y为混合像元光谱；M=[m1,m2,…,mn]，mi为L*1的端元，L为图像波段数；a=[a1,a2，…，an]，ai为1×k的像元丰度，k为图像像元个数；ε为噪声；非线性变换g(·)采用二阶多项式的形式：

(8)

该式表示将长度为L的向量s=[s1,s2,…,sL]映射为每个元素均为一个二次多项式的向量，b为调整非线性效果大小的参数. 将式(8)代入式(7)，同时考虑丰度的物理意义，由此得到后验多项式非线性混合模型的具体表达形式：

Y=Ma+b(Ma)⊙(Ma)+ε.

(9)

当b为0时，该模型退化为线性混合模型.

2.1.6 NCM光谱解混模型 LMM模型和PPNMM模型都是假设所“看到”的物质是确定不变的，然而在真实的地表环境中，环境条件、光照、大气以及时间的变化导致地物光谱发生一定的变异. 正态组分模型(Normal Compositional Model，NCM)是线性光谱混合模型的一种扩展：用概率来描述光谱的不确定性，将端元视为一个呈给定概率分布的随机变量，利用特定参数来表示光谱变异性[32]. NCM模型认为每一个像元的光谱构成如下：

(10)

其中，mr为端元，从影像中提取，是独立的高斯向量，是可变的端元部分. 该式中没有加入额外的噪声，是由于该模型中的端元具有不确定性.

2.2 无人机影像实验

为了更好地研究植被覆盖度估算模型的精度并进行适应性评价，通过对影像进行裁剪，将5 m×5 m的正方形小区域作为一个样方. 选取研究区域内较具有代表性的33个样方进行实验，兼顾了高植被覆盖度区域和低植被覆盖度区域2种情况.

根据选取的样方，分别使用上文所述的6种植被覆盖度估算方法进行实验. 对于纯土壤像元，其NDVI值在理论上应当近似为零，但由于土壤类型、土壤粗糙度、土壤颜色、土壤含水量和环境等因素的干扰，NDVIsoil一般在-0.1～0.2之间[26]. 通常情况下，分别以置信区间内的最大值、最小值来表示NDVIveg、NDVIsoil[21]. 本研究使用无人机影像数据 提取NDVI,并对NDVI进行统计，将频率统计表与研究区植被的实际情况相结合，最终选取NDVIsoil、NDVIveg的值分别为0.15、0.82，将其代入式(3)和式(4)，即可得到像元二分模型和Carlson模型估算的植被覆盖度. 对于Baret模型，Kp/KVI值会随着植被的生长、叶面积指数的不同和叶面透过率的不同等而改变，但在通常情况下，可以采用实验中的经验值来确定. 文献[27]提出NDVI所对应的Kp/KVI的实验值为0.617 5；文献[25]进一步改进了Baret模型，认为当Kp/KVI=0.654 5时的估算效果更佳. 因此，本文中Baret模型采用下式估算植被覆盖度：

(11)

对于3种光谱解混模型：LMM模型、PPNMM模型和NCM模型，首先从图像上选取用于解混的端元，再根据相应的光谱解混方法(式(6)、(9)、(10))进行丰度求解，最后根据下式计算植被覆盖度：

(12)

其中，aveg,i为第i个像元的植被丰度值，n为一个实验样本的总像元个数.

2.3 精度评价方法

本研究主要通过以下2个指标定量化评价植被覆盖度估算模型的估算精度：一是均方根误差(RMSE)，目的是对模型植被覆盖度估算结果进行残差分析，RMSE越小表示估算精度越高；二是植被覆盖度估算平均相对误差(Ef)，Ef越小表示模型估算精度越高. RMSE和Ef的计算公式如下：

(13)

(14)

3 结果与分析

为了研究基于无人机高光谱影像的像元二分模型、Carlson模型、Baret模型、LMM模型、PPNMM模型和NCM模型估算植被覆盖度的估算精度和适用性：首先，使用6种模型分别估算33个样方的植被覆盖度；然后,对估算的植被覆盖度进行精度评价；最后，结合实际的应用场景，探讨6种模型的适用性.

3.1 验证数据的获取

为了验证植被覆盖度的估算效果，在研究区域相同位置获取50 m飞行高度的无人机高光谱影像，用于构建实验验证数据. 该影像幅宽为13.93 m、空间分辨率为2.18 cm，影像的预处理与400 m飞行高度的影像处理方式相同. 相比于400 m飞行高度的影像，该影像具有更高的空间分辨率，能够更清晰地反映真实地物的分布情况；相比于航空航天遥感数据，该影像也具有更高的空间分辨率：在空间分辨率为2.18 cm时，已消除了大量混合像元的存在，可以很准确地提取植被分布信息，满足验证精度要求. 本研究通过评价多种监督分类方法(最大似然分类、马氏距离分类、最小距离分类和支持向量机(Support Vector Machine,SVM)分类方法)的分类结果，选择精度最高的监督分类方法来构建验证数据. 验证数据的构建步骤如下：首先，裁取各样方对应位置的50 m飞行高度的无人机影像数据；然后，通过监督分类方法将研究区域内的地物分为植被和非植被2类，以目视解译方式和分类精度验证分类结果；最后，根据分类结果统计植被类别面积占比，得到各样方的植被覆盖度验证数据. 在图像进行分类前，根据实地考察的先验知识，采用图像目视判读的方法，分别在各个样方上选取500个验证点，以此对上述监督分类方法的分类结果进行精度评价. 分类结果(图3)显示：SVM分类结果的精度最高(达到99.2%)，说明该方法的分类结果可作为植被覆盖度验证数据. 同时，由文献[33]可知，将SVM分类结果作为植被覆盖度真实值有一定可靠性. 因此，以SVM分类结果统计得到的植被类别的占比作为样方的植被覆盖度的验证数据.

图3 无人机影像及4种分类方法的分类结果

3.2 结果与精度评价

使用上文所述6种模型估算各个样方的植被覆盖度，再获取对应样方的验证数据，以进行对比分析. 由实验结果(图4)可知：(1)6种植被覆盖度估算模型的相关系数均大于0.9，说明6种植被覆盖度估算模型与植被覆盖度都有较好的相关性. (2)像元二分模型的估算值多位于y=x的上方，有明显高估植被覆盖度的现象；而Carlson模型的估算值多位于y=x的下方，明显低估了植被覆盖度；Baret模型在低植被覆盖度区域内(即FVC<0.5)出现明显高估的情况，而在高植被覆盖度区域内(即FVC≥0.5)出现明显低估的情况. (3)从整体上来看，光谱解混模型(LMM模型、NCM模型和PPNMM模型)的估算值与验证值之间的相关性高于经典模型(像元二分模型、Carlson模型和Baret模型)的，与y=x的拟合程度也优于经典模型的，说明光谱解混模型估算的植被覆盖度的精度高于经典模型的.

图4 6种模型的植被覆盖度估算值与验证值的拟合

对6种植被覆盖度估算模型的估算结果进行定量化精度评价，由评价结果(表1)可知：(1)NCM模型估算的植被覆盖度的均方根误差最小(RMSE=0.040 1). (2)NCM模型估算的植被覆盖度的平均相对误差为7.53%，明显小于其他植被覆盖度估算模型的. (3)从模型拟合线与参考线y=x来看，Carlson模型、LMM模型、NCM模型的线性拟合线与y=x更为接近，而像元二分模型、Baret模型和PPNMM模型的线性拟合线与y=x的相差较大，说明这3个模型估算的偏移程度较大，适用性较低. 综上可知，像元二分模型、Baret模型和PPNMM模型估算的植被覆盖度的精度较低；Carlson模型虽然拟合效果较好，但其RMSE和平均相对误差均较大，表明其估算的植被覆盖度的精度也较低；LMM模型和NCM模型估算的植被覆盖度的精度较高，其中，NCM模型估算的植被覆盖度的均方根误差最小、平均相对误差最小且线性拟合线与y=x较为接近，总体上说明NCM模型估算植被覆盖度的效果最好.

表1 6种模型估算植被覆盖度的精度评价Tabel 1 The evaluation of the accuracy of the estimation of vegetation coverage with 6 models

为了更进一步探索模型的适用性，将实验区域划分为低植被覆盖度区域(FVC<0.5)和高植被覆盖度区域(FVC≥0.5)，分别对6种模型逐一进行评价. 由评价结果(表2、表3)可知：(1)在低植被覆盖度区域，NCM模型估算的植被覆盖度的均方根误差和平均相对误差最小，分别为0.039 5和11.18%，说明NCM模型的估算效果最好. 其他5种模型估算的植被覆盖度的均方根误差和平均相对误差都相对较大，线性拟合线与y=x有明显偏移，说明模型估算效果较差. (2)在高植被覆盖度区域，LMM模型估算的植被覆盖度的均方根误差最小(RMSE=0.039 8),平均相对误差较小(Ef=5.05%);NCM模型估算的植被覆盖度的平均相对误差最小(Ef=4.49%)，均方根误差(RMSE=0.040 5)略高于LMM模型的. 考虑到平均相对误差一般衡量数据的可信度，而在评价估算值与真实值之间的效果时，均方根误差更能反映结果的好坏，因此判断LMM模型的估算效果略优于NCM模型的. 同时，LMM模型和NCM模型的线性拟合线与y=x均较接近，说明这2个模型的估算值都非常接近验证值且估算效果较稳定. (3)从整体上看，NCM模型、Carlson模型和Baret模型在低植被覆盖度区域的估算效果优于在高植被覆盖度区域的；而其他3种模型在高植被覆盖度区域的估算效果均优于在低植被覆盖度区域的，其中LMM模型尤为明显：在低植被覆盖度区域估算的植被覆盖度的均方根误差为0.074 4，在高植被覆盖度区域估算的植被覆盖度的均方根误差为0.039 8，误差减小将近一半.

表2 低植被覆盖度区域的估算精度评价Tabel 2 The evaluation of the accuracy of the estimation of fractional low vegetation coverage area

表3 高植被覆盖度区域的估算精度评价Tabel 3 The evaluation of the accuracy of the estimation of fractional high vegetation coverage area

综上所述，基于无人机影像估算植被覆盖度，光谱解混模型的估算效果优于经典模型的． 从理论上分析，经典模型在一定程度上极大地依赖经验值，如像元二分模型和Carlson模型的置信区间、Baret模型的Kp/KVI值均依据具体实验的经验值来确定[24-25]，从而导致估算结果的误差随着实验区域的不同而变化，出现时好时坏的情况． 另外，经典模型依靠植被指数，在常用于计算植被指数的波长范围内存在较多的波段，从而导致估算的植被覆盖度存在一定的不确定性误差． 而光谱解混方法以反射率光谱为基础，通过反演的方式推算地物的混合情况，在一定程度上减小了偶然误差，从而能更准确地估算植被覆盖度． 3种光谱解混模型的估算效果中，NCM模型的估算效果最好，PPNMM模型的估算效果最差；在高植被覆盖度区域，LMM模型的估算效果与NCM模型的估算效果相近． 究其原因为：植被存在明显的光谱变异性，LMM模型仅考虑了物质间的线性混合，没有考虑光谱的变异性；PPNMM模型考虑了地物间的多重散射、多种物质非线性混合，但没有考虑光谱的变异性；NCM模型在一定程度上考虑了“同物异谱”的情况，因此获得了最高的估算精度．

4 小结与展望

本文基于无人机高光谱数据，对6种植被覆盖度估算模型进行了对比分析. 研究结果表明：(1)LMM模型、NCM模型和PPNMM模型的估算效果优于像元二分模型、Carlson模型和Baret模型的估算效果. (2)像元二分模型高估了植被覆盖度，Carlson模型低估了植被覆盖度，Baret模型在低植被覆盖度区域出现明显高估的情况、在高植被覆盖度区域出现低估的情况. (3)NCM模型估算植被覆盖度效果最好；在高植被覆盖区域，LMM模型估算植被覆盖度的效果与NCM模型估算植被覆盖度的效果相近．

本研究存在一些亟待解决的问题：第一，由于无人机影像的获取过程缺少一定的地理定标参考，并且在低空飞行获取超高分辨率图像时所获取的幅宽较小，需要多条带飞行才能获取一定范围的影像，导致在影像拼接、几何校正时很难保证不同分辨率的两景无人机影像之间的偏移控制在亚像元尺度内，从而难以进行大范围的样方研究；第二，由于无人机的数据区域较小，对于大范围的植被覆盖度的估算，混合像元分解模型适应性如何，有待进一步研究.