基于ARIMA模型对我国货币供应量的分析

文/高晓洁

（上海大学悉尼工商学院）

一、引言

（一）研究意义

货币供应量的变化反映了一国央行货币政策的变化，当货币供应量大幅增加时，就可能引起通胀或国际收支恶化，导致宏观经济失衡；而货币供应量的不足同样会阻碍经济的发展。

因此，一个稳定适度的货币供应量对宏观经济平稳运行具有很重要的现实意义，通过货币供应量可以从总量上把握我国货币供应与经济发展总体态势。

本文将计量经济模型中的理论和时间序列预测方法运用到货币供应量的研究之中，从而得出一些有建设性的结论及建议。

（二）研究内容

本文使用1996年1月到2019年12月的我国货币供应量（M2）月度数据，在消除了序列异方差、趋势性、季节性之后，对数据进行建模，并根据信息准则AIC选择其中拟合结果最好的一个模型，即ARIMA(2,1,3)(1,1,1)12，对2020年1-5月的货币供应量（M2）进行预测。结果显示，预测值与实际值比较接近，比较准确地预测了我国货币供应量走势。

其中3-5月的实际值比预测值偏高，这可能是受到上半年货币宽松政策的影响。随后本文将2020年的5期实际数据纳入后重新拟合模型，并再次预测，得到2020年底的货币供应量为2245592亿元，这一结果与2019年底的1986488.82亿元相比，增长了13.04%。

二、相关文献评述

在国外，Friedman&Schwartz在其著作《美国货币史》中通过对美国近百年的数据(1867-1960)资料进行研究，证明了货币能够对产出造成影响[1]。 Stock&Watson研究了110个国家长达30年的数据后得出结论，通货膨胀和长期货币供应量呈显著正相关，但货币供应量对实际产出几乎没有影响[2]。Walsh对货币供应量与产出之间的实证研究，并对货币供应量与产出之间的关系的实证检验方法作了简单全面的介绍[3]。Brandt&Zhu通过对经济增长波动性与通货膨胀的循环影响关系，发现我国的通货膨胀在改革之后部分地反映了货币政策[4]。

在国内，研究论述货币供应量的文章很多，也取得了许多成果。刘斌运用协整与误差修正模型，对我国的货币需求与供给进行了定量研究，同时用建立的模型在不同时段进行了预测[5]。徐龙炳建立了VAR模型，并使用了冲击响应函数方法和工具，以此来研究我国20世纪80年代以来各个时间区间的货币政策传导效果[6]。陆军、舒元使用Granger因果检验，研究了我国货币供应量对实际产出的影响效应，得到的结论是，无论是预期到的还是未预期到的货币供应量变动都会影响产出，在10%的显著性水平下，央行的货币政策对实际产出存在非对称影响[7]。邓雄、蒋中其的研究表明，在众多影响货币供应量的因素中，GDP的作用是最大的，当一国的GDP增长时，货币供应量往往也会同步增加[8]。

本文在以上研究成果的基础上，对我国货币供应量（M2）的波动做进一步的探索分析，建立模型，并通过预测来检验模型的准确性。

三、数据与实证分析

（一）数据来源

本文选取1996年1月至2020年5月的我国货币供应量（M2）月度数据。数据来源于wind。首先使用1996年1月至2019年12月的月度数据拟合了预测模型，并得到了2020年1月至2020年12月的货币供应量预测值。在模型结构和预测误差这两方面都取得了较好的结果。

（二）平稳性检验

通过利用R软件对我国货币供应量绘制时序图（如图1），可以清晰地了解到M2序列具有显著的增长趋势，是非平稳时间序列。并且可以发现，M2的走势具有指数趋势。需对M2进行平稳化处理后再进行建模。

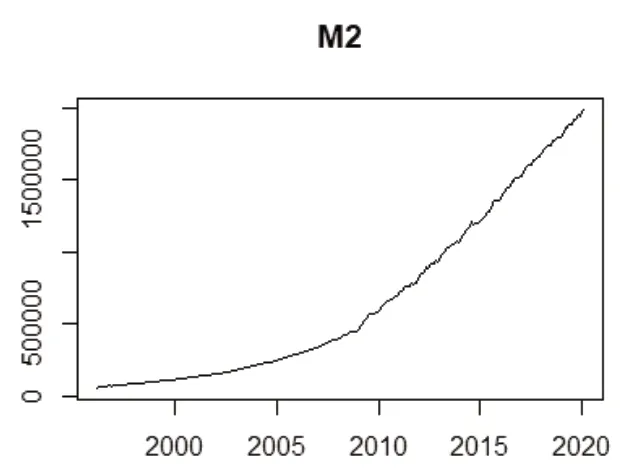
图1 1996-2019年我国货币供应量（M2）时序图

为了消除异方差，对该序列做对数变换，变换后的时序图（如图2）所示。

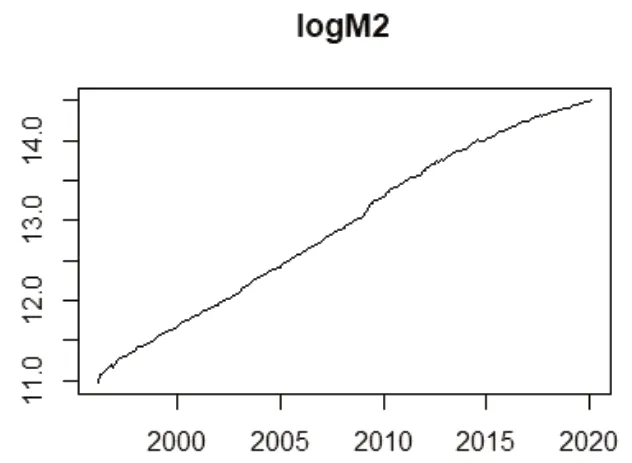
图2 1996-2019年我国货币供应量（M2）对数时序图

图2显示，取对数后的货币供应量（M2）时序图仍然具有线性递增的趋势，还需要对该序列进行一阶差分运算来实现趋势平稳。结果如图3所示。

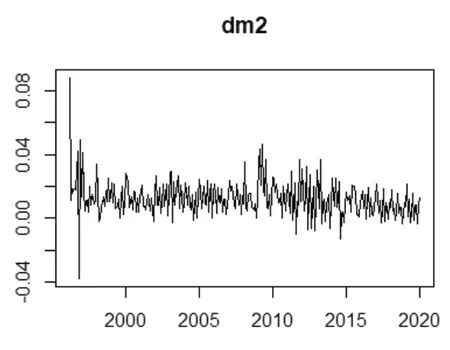
图3 1996-2019年我国货币供应量（M2）对数一阶差分时序图

一阶差分后的货币供应量序列没有明显的趋势性，但对其进行滞后期为12的ADF检验时，得到P值为0.1589。说明一阶差分后的序列存在季节性，需要进一步做差分。

对序列作季节差分后，进行ADF检验，得到P值＜0.01，在1%显著性水平下拒绝原假设，说明该序列平稳。

由图4可见，序列的样本自相关与偏自相关系数很快落入随机区间，故序列趋势已基本消除，但在滞后期为12时取值仍然较大，季节性依然比较明显。经试验，对序列进行二阶季节差分，发现序列季节性并没有得到显著改善，故只做一阶季节差分即可。

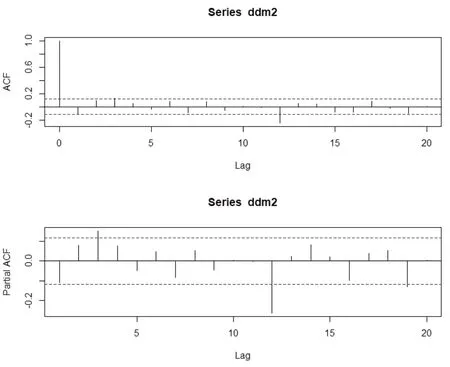
图4 序列自相关和偏自相关图

（三）模型识别

因为经过一阶逐期差分，序列趋势消除，故d=1；经过一阶季节差分，季节性基本消除，故D=1。所以选用ARIMA(p,1,q)(P,1,Q)12模型。模型阶数的确定取决于对自相关和偏自相关函数的分析。观察图4，偏自相关图显示p=3比较合适，自相关图显示q=3。为了检验模型的拟合程度和预测精度，本文选择多个(p,q)组合进行尝试，选择的(p,q)组 合 有：(3,3),(2,3),(3,2),(2,2)。由于滞后阶k=12时，样本自相关和偏自相关系数都显著不为0。所以，P=Q=1。

（四）模型建立及检验

根据以上分析，我们知道要 建 立ARIMA(3,1,3)(1,1,1)12、ARIMA(2,1,3)(1,1,1)12、ARIMA(3,1,2)(1,1,1)12、ARIMA(2,1,2)(1,1,1)12四 种模型。各模型拟合结果及检验结果见表1至表4。

表1 模型ARIMA(3,1,3)(1,1,1)12拟合结果

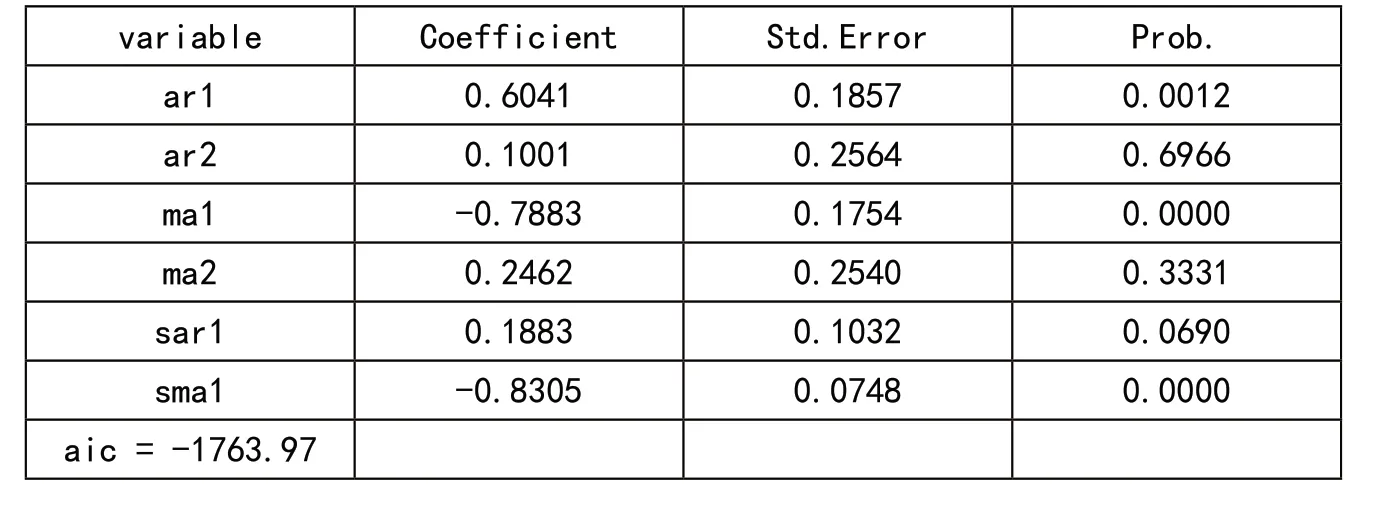
表4 模型ARIMA(2,1,2)(1,1,1)12拟合结果

比较表中各个模型的检验结果，第二个模型的AIC值最小，所以选择ARIMA(2,1,3)(1,1,1)12模型比较合适，其展开式为：

（五）模型预测

利用上述得到的ARIMA(2,1,3)(1,1,1)12模型，对2020年的货币供应量进行拟合预测，并与2020年1-5月份的实际值进行比较。得到结果如表5所示。

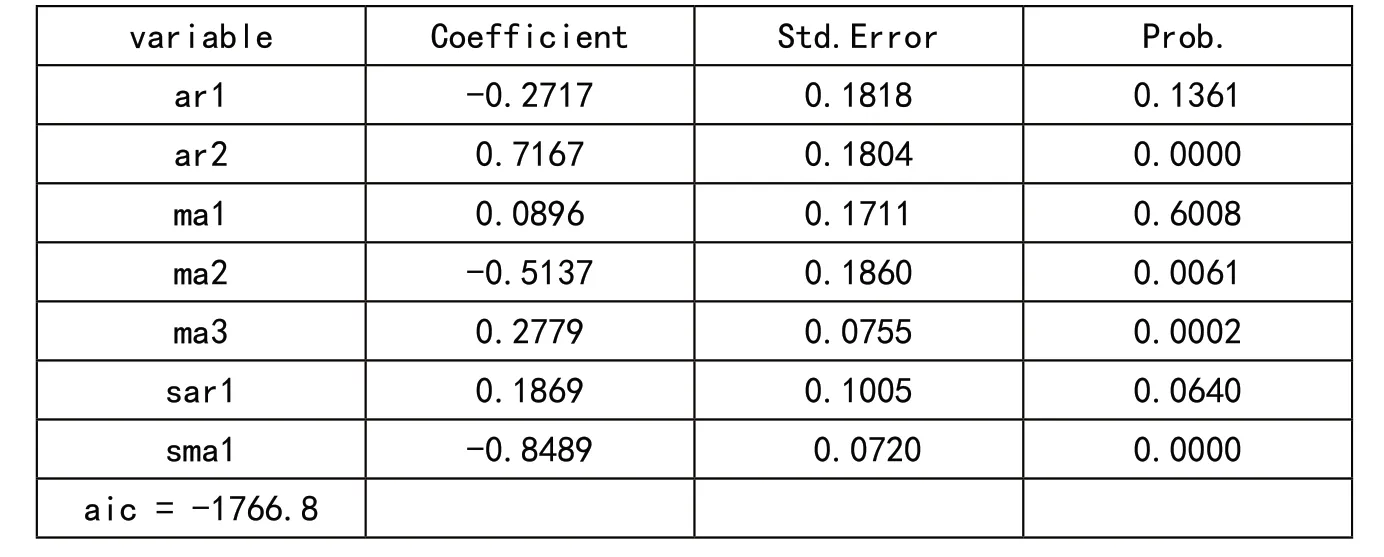
表2 模型ARIMA(2,1,3)(1,1,1)12拟合结果

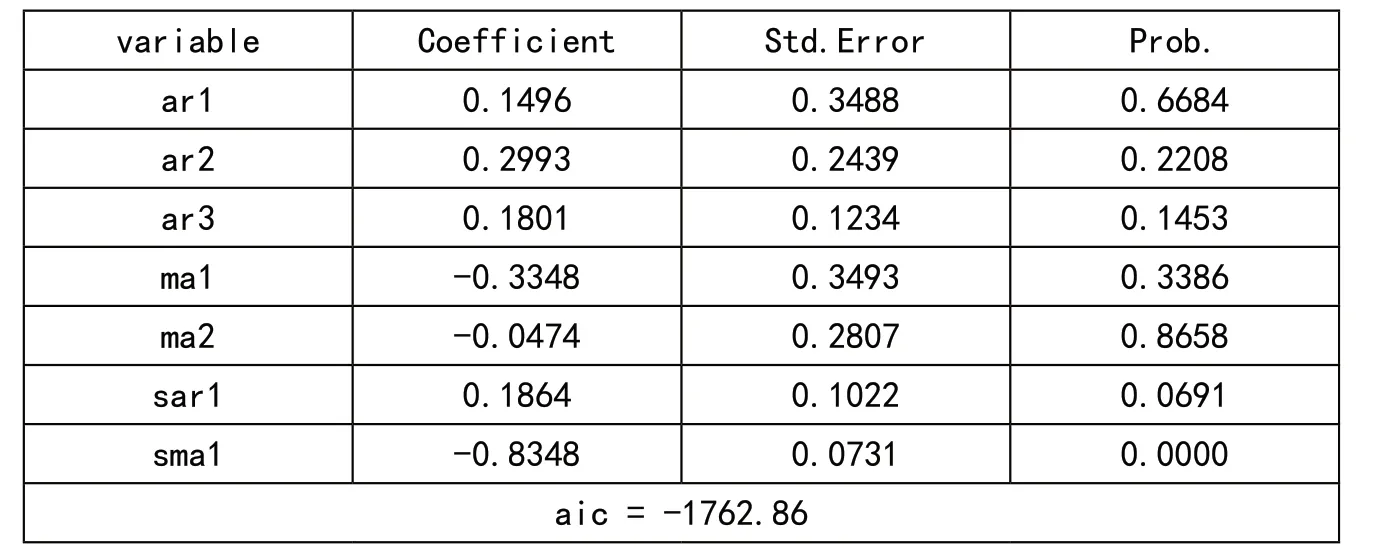
表3 模型ARIMA(3,1,2)(1,1,1)12拟合结果

由 表5可 以 看 出， ARIMA(2,1,3)(1,1,1)12模型拟合的2020年1月至2020年5月数据各月的误差百分比都很小，大多控制在1%以内。这说明模型对未来货币供应量的预测基本符合实际情况，并且预测结果是比较可靠的。

表5 ARIMA(2,1,3)(1,1,1)12模型的货币供应量预测结果

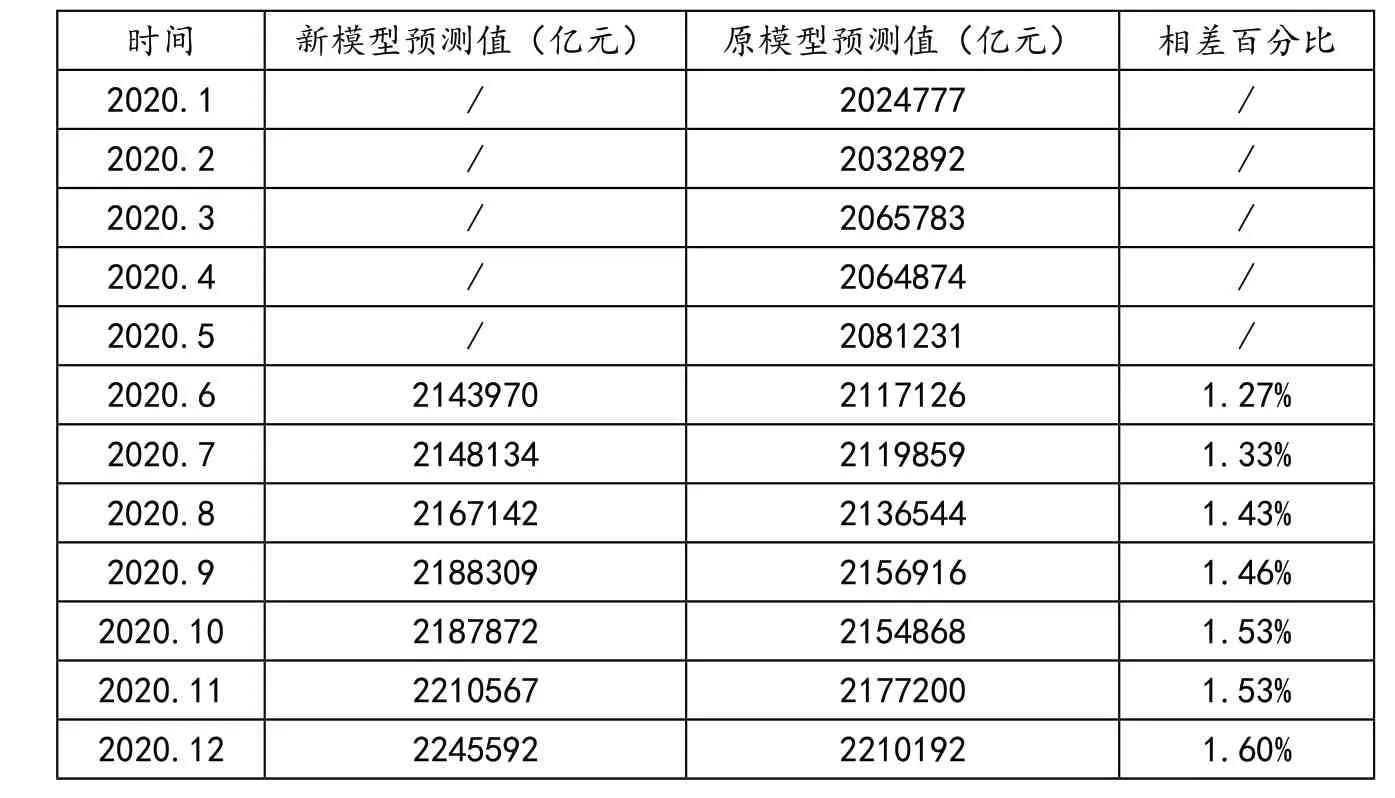
表7 两次预测值对比

2020年由于受到新冠疫情的冲击，包括我国在内的各国央行都采取了一系列货币宽松政策，这可能也是3-5月货币实际值略高于预测值的原因。

接下来将2020年的前5个月的数据纳入，再次拟合ARIMA(2,1,3)(1,1,1)12模型，并用新模型预测未来的货币供应量。得到拟合结果与预测结果如表6所示。

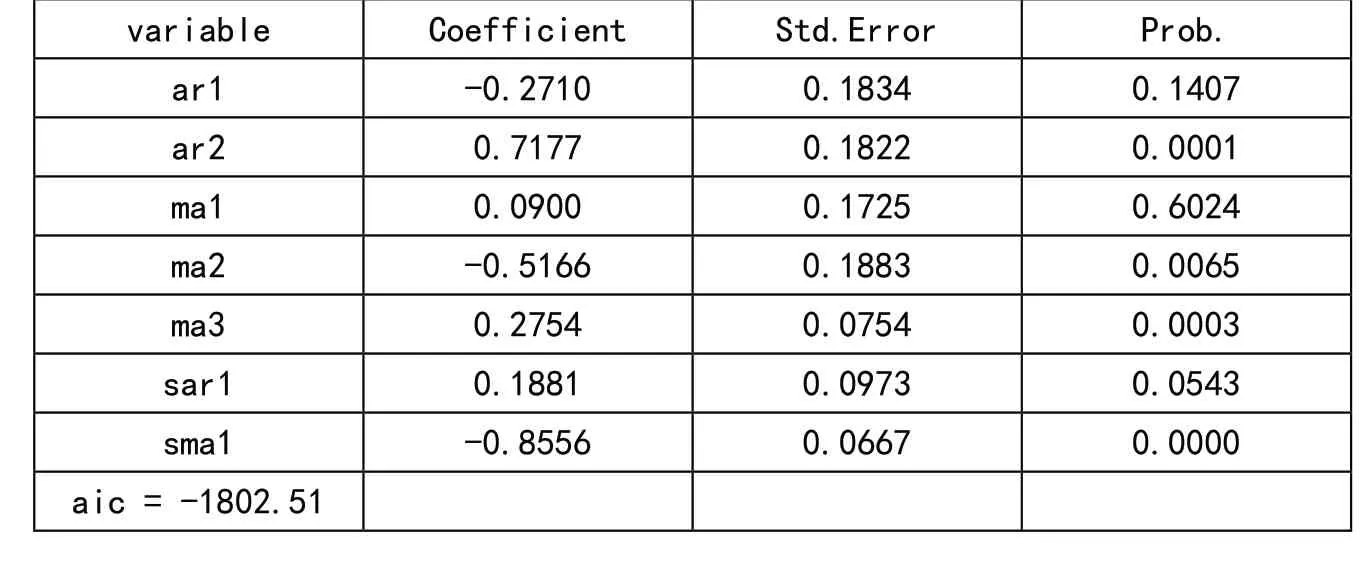
表6 模型ARIMA(2,1,3)(1,1,1)12拟合结果

将2020年前5个月的货币供应量数据纳入后，得到的新预测值普遍比原模型预测值高出1个多百分点。在纳入上半年的货币宽松政策影响后，由新模型预测的2020年底的货币供应量为2245592亿元，在一定程度上代表了我国货币供应量的走势，对描述货币供应量波动特征方面有一定的借鉴意义。进一步讨论，由ARIMA模型预测得到2020年底的货币供应量（2245592亿元），与2019年底的1986488.82亿元相比，增长了13.04%。

四、结语

本文介绍了符合金融系统预测规律的ARIMA(p,d,q)(P,D,Q)s时间序列模型。建模的样本期从1996年1月到2019年12月，消除了序列异方差、趋势性、季节性之后，对数据进行模型识别，建立了模型ARIMA(2,1,3)(1,1,1)12。它在拟合2020年1-5月的货币供应量中预测精度较高，比较准确地预测了我国货币供应量走势，可为我国货币供应量的预测提供可靠的参考依据。

由上文分析可以知道，货币供应量受到许多因素不同程度的影响，加上自身具有季节性，比如我国的春节、国庆节等都会对其带来较大影响。一个稳定适度的货币供应量对宏观经济平稳运行有很重要的现实意义，可以从总量上把握我国货币供应与经济发展总体态势。