初中生平面几何解题中运用元认知策略的调查研究

宋移飞,李 杭，徐 伟

(鞍山师范学院 数学与信息科学学院,辽宁 鞍山 114007)

1 问题的提出与理论依据

平面几何解题活动对初中生具有一定困难，为此，平面几何解题的教学对初中教师构成一定的挑战.波利亚[1]认为，掌握数学就意味着善于解题；罗增儒[2]认为，数学学习中真正发生数学的地方都无一例外地充满着数学解题活动.可见，学生是否善于解题已经成为数学学习的关键因素.几何解题的思维特征关乎对问题情境的整体感知，即使通过审题初步拟定解题计划后，在解题过程中仍然面临调整解题思路的问题.因此，通常意义下的几何解题思维需要较多地使用元认知策略.

20世纪70年代，美国心理学家弗拉维尔提出元认知的概念，并给出元认知是以各种认知活动的某一方面作为其对象或对其加以调节的知识或认知活动的定义[3].元认知的核心意义是“关于认知的认知”.随着这一理论的提出，元认知理论成为教育心理研究的主流问题.董奇[4]指出元认知结构分为元认知知识、元认知体验和元认知监控；龙毅[5]指出元认知包括元认知知识、元认知体验和元认知监控，初步将元认知进行划分且与数学学科建立联系；崔宝蕊、李健、王光明[6]将数学元认知划分为数学元认知知识、数学元认知体验、数学元认知监控3个维度，更加具体地分析了元认知所包含的各个策略；波利亚在《怎样解题》一书中给出怎样解题表，将解题活动分为理解题目、拟定计划、执行计划、回顾等4个步骤；侯乐旻[7]认为元认知监控在很大程度上影响着个体对学习过程和学习结果的判断，能够帮助个体调整学习行为；章建跃、林崇德[8]指出在整个数学学习过程中将自己的数学活动作为意识对象，对其进行积极主动的计划、检验、调节和管理，以实现学习活动中的自我监控，这对解几何题活动而言尤为重要.

关于元认知策略与解题理论的研究成果较多，但元认知策略与具体的平面几何解题相结合的研究较少.本研究基于元认知策略理论和波利亚解题理论，将学生平面几何解题活动中运用元认知策略情况的具体指标划分为计划策略、监控策略、调节策略3个维度，各维度下又具体分为题设、整体问题情境、方法与策略3个子维度，目的是调查八年级学生在平面几何解题思维活动中元认知策略的运用情况.

2 研究设计

2.1 研究对象

从某城市两所中学中各抽取3个班级(均为八年级)共210名学生进行调查研究，发放问卷210份，回收问卷210份，剔除无效问卷17份，得到有效问卷193份，有效回收率为92%.对调查问卷结果进行筛选，选择有效问卷数量偏高的两个班级发放测试卷共64份，回收64份，剔除4份无效测试卷，得到有效测试卷60份，有效回收率为94%.

2.2 研究工具及指标分析

根据已有的研究成果，结合实际教学中的课堂观察和作业批改，以及学生解几何题思维的实际表现，初步拟定问卷题目，描述学生在一般意义下解题活动中使用元认知策略的意愿情况.问卷题目共16题，包括计划策略5题、监控策略6题(第9题为反向计分题)和调节策略5题.采用李克特(Likert)五点计分法，选项制定为非常符合、符合、基本符合、不符合、非常不符合，分别赋5、4、3、2、1分.对部分问卷进行前测和数据分析，在征求专家意见后对问卷题目进行了修改，初步确定“影响平面几何解题活动因素的调查研究”问卷.

测试卷的编制建立在理论研究和实际教学观察的基础上，并征求一线教师及专家的意见进行多次修改，初步编制出“等腰三角形”测试卷.测试卷题目共7题(满分80分)，难度分布为：简单难度3题(每题10分)，中等难度2题(每题12分)，较难题目2题(每题13分).

通过文献分析和对已有研究成果的研究，初步拟定学生在平面几何解题活动中运用策略的具体指标，结合一线教师、专家的意见，经多次修改最终确定具体指标.解题活动中作出何种解题行为可反映其采用的相应元认知策略.结合波利亚解题的4个步骤，将学生解题过程中3个策略的运用维度再进一步划分为局部题设、整体问题情境、方法与策略3个方面，根据解题活动中所使用不同层次的策略分别赋1、2、3、4分，具体划分如表1所示.

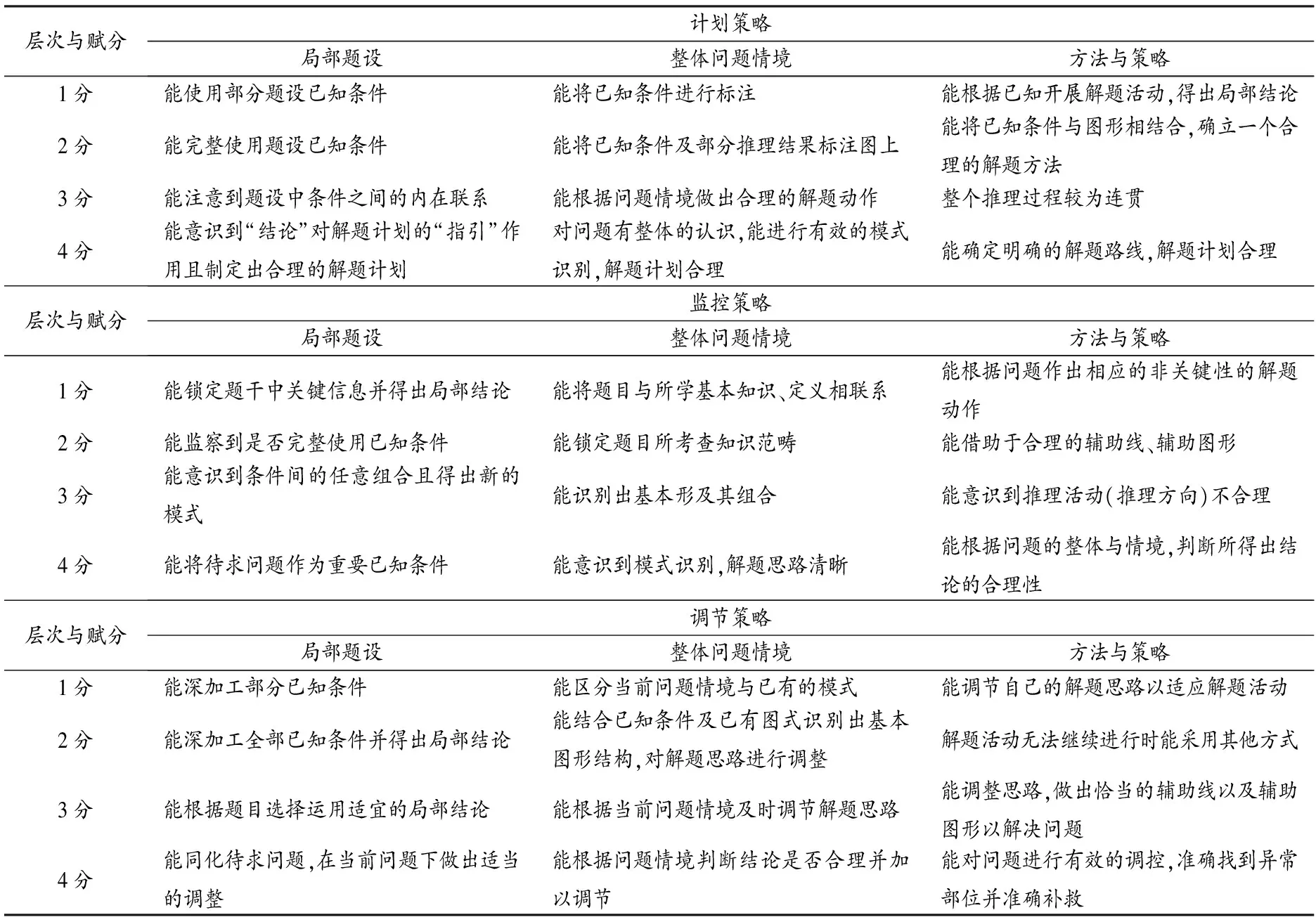
表1 测试卷评价标准

对指标进行信效度检验，结果如表2所示.

表2 指标可靠性检验

2.3 研究方法

问卷调查法：发放“影响平面几何解题活动因素的调查研究”问卷.

测试法：发放“等腰三角形”测试卷，对回收的数据运用SPSS 20.0软件进行统计分析.

2.4 研究过程

(1)通过阅读文献了解元认知策略运用于各学科的情况，尤其是与数学学科相结合的研究成果.

(2)结合已有的研究成果和学生实际的学习过程，征求专家意见拟定学生平面几何解题活动中运用元认知策略的评价指标.

(3)利用SPSS 20.0软件分析回收的问卷和测试卷数据.

3 测试及分析

3.1 问卷分析

据文献[9]，信度在0.8～0.9较好，在0.7～0.79之间也可使用.对问卷采用科隆巴赫信度进行分析，结果如表3所示.由表3可知，系数为0.806，符合测量标准.

表3 问卷可靠性检验

对各维度均分进行数据分析，结果如表4所示.由表4可知，学生在平面几何解题活动中对各个策略的使用倾向由高到低依次为计划策略、监控策略、调节策略.

表4 问卷各维度均分

3.2 测试卷分析

对两个班级共60份测试卷进行统计分析，得出测试卷的信效度，如表5所示.由表5可知，系数为0.988，符合测量标准.

表5 测试卷可靠性检验

对两个班级共64人进行测试，剔除无效问卷4份，对60份测试结果按表1中测试卷评价标准对策略运用的情况进行赋分，同时按照一线教师评价测试卷的结果进行实际得分的统计，将被测试人数按此次答卷实际得分由高到低划分为排名靠前组(1～20)；排名居中组(21～40)；排名靠后组(41～60).对实际得分与策略得分进行相关性分析，结果如表6所示.

表6 各策略得分与实际得分相关性

由表6可知，计划策略、监控策略、调节策略都与实际分数呈现显著的相关性，通过比较分析可以得出，3个策略的相关性由高到低依次是计划策略、调节策略、监控策略.此结论与调查问卷得出的结论不一致，为探究原因，对3组学生分别进行各题得分统计.通过对比3组学生实际得分与策略得分可知，排名靠前组和排名居中组对策略的使用符合调查问卷的结论，而排名靠后组学生更多地使用调节策略，结果如图1所示.

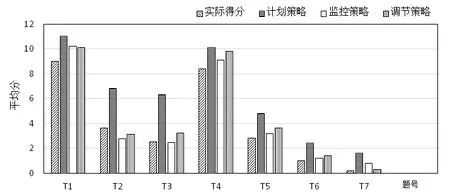
图1 测试成绩靠后组策略使用情况统计图

对测试成绩靠后组进行答题分数统计分析，由图1可观测出学生在解题活动中对于计划策略的使用仍然较高于其他策略，而调节策略高于监控策略.

4 研究结论与建议

4.1 结论

(1)通过对193份问卷进行统计分析，得出结论：一般意义下，学生在解题活动中使用策略意愿为计划策略的使用显著高于监控策略和调节策略，监控策略和调节策略相近.

(2)通过对测试卷进行分析，得出被测学生在解题活动中使用策略的频率由高到低依次为：计划策略、调节策略、监控策略.对于成绩靠后组的学生而言，他们在解题受阻时会出现频繁转换解题方向和路径的情况.

4.2 建议

在平面几何解题活动中，计划策略作为引导解题活动的方向和解题步骤的开始阶段能够受到学生学习和教师教学的充分重视，但在解题活动中有效地运用监控策略和调节策略并没有得到重视，甚至在解题后反思策略的使用环节仍然难以使学生认识到元认知策略的运用对于成功解题的重要性.这说明，元认知策略的使用在日常的几何解题教学活动中没有被充分重视，因此，在学生的学习和教师的教学中应当加强监控策略与调节策略的学习和培养.

(1)教师在平面几何解题教学活动中，在基本定义、基本命题、解题策略教学的基础上，应当侧重培养学生在平面几何解题活动中运用元认知策略的能力.教师在教学中可以围绕几何问题开展以目标为导向、实现目标需要哪些步骤的探究活动，从而培养学生拟定计划的能力；教师在教学中加强基本形的教学，加强对学生已有图式的拓展，帮助学生建立有效的模式识别能力，从而有助于培养其监控能力；教师在教学中应当帮助学生获得几何概念、命题的多种形式表征以适应不同问题的情境，从而培养学生的调节能力.

(2)教师在几何解题教学过程中，要指导学生按照解题过程对问题进行系统的分析，对问题从整体情境到具体细节的思维流程进行分析.同时，在执行解题计划的过程中，学生应时刻监控自己的解题状态，加强自我监控和调节能力.