双三角高程法实现高度测量实验仪器的改进与应用
2022-01-10崔群
崔 群
(鞍山师范学院 物理科学与技术学院,辽宁 鞍山 114007)
高度测量作为物理实验课长度测量实验的教学内容,通常使用游标卡尺、测高仪、直钢尺、钢卷尺等实验设备实现.游标卡尺、测高仪的量程通常不超过30 cm,直钢尺、钢卷尺的量程通常不超过3 m,无法实现工程测量中大地高程和建筑物高度一级的参数测量.本文将实验室常用的测高仪进行新的结构设计和功能设计,可以通过两次三角高程测量,不需要直接进行水平距离测量实现建筑物的高度测量.
1 工程测量中高度测量的常用方法及原理
工程测量中大地高程和建筑物高度测量的常用方法有水准测量、经纬仪三角高程测量、全站仪三角高程测量、GPS高程测量等方法,全站仪三角高程测量又分为单向、对向、中点观测3种[1-3].其中适合物理实验教学讨论的为近距离大地高程测量和建筑物高度测量,测量方法可以采用经纬仪、全站仪单向三角高程测量.如图1所示,单向三角高程测量原理就是把测量仪器架设在测量点A,把棱镜架设在目标点B,测量出B点相对于A点的竖直角αAB与水平距离SAB,设KAB为大气折光系数,R为地球半径(6 371 km),IA为A点仪器高,VB为B点仪器高,则两点的高程差hAB为[2]:
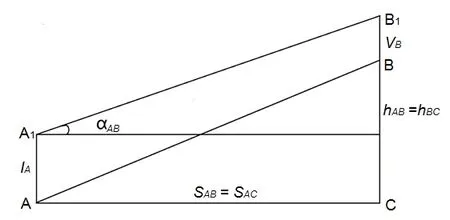
图1 单向三角高程测量原理
(1)
各种三角高程测量中,水平距离SAB为必须测量的参数,最原始的方法为直接用钢尺测量[1],全站仪则采用先进的激光测距,前者精度过低,后者实验室没有直观教学可行性.本文设计了一款不需要直接测量水平距离便可以实现高度测量的实验仪器,可以较好地实现教学功能.
2 物理实验室791型测高仪的改进
2.1 物理实验室791型测高仪的长度测量功能
791型测高仪为20世纪80年代生产的一款长度测量仪器,作为物理实验室通常的长度测量教学仪器使用,图2为其结构简图.其固定底座由3个微调螺栓支撑用以调节水平状态,在固定底座上安装有水平方向可移动的水平滑块,移动距离由固定底座与水平滑块组成的最小分度为0.05 mm的游标卡尺测量,量程为150 mm.在水平滑块上安装有垂直立柱,垂直度由仪器制作精度决定.立柱上安装有垂直方向可移动的环形滑块,滑块上安装一个望远镜,与滑块同步移动,移动距离由立柱与滑块组成的分度为0.05 mm的游标卡尺测量,量程为280 mm.望远镜上安装一个水平仪,可以通过滑块上的微调旋钮调节俯仰达到水平状态,通过手工握持固定扶手实现滑块整体的上下移动,立柱可以通过扶手实现绕轴水平360度旋转.
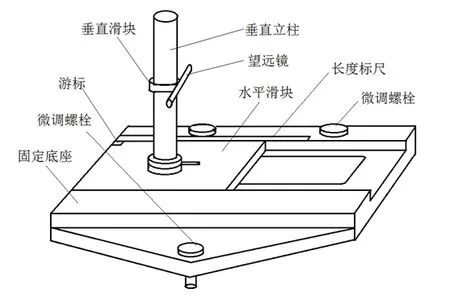
图2 791型测高仪结构简图
791型测高仪的主要功能是可以实现无接触长度测量.当固定底座和望远镜分别调整到水平状态时,可以在望远镜的有效视距内测量物体水平方向的长度和垂直方向的高度.具体测量方法是将被测量物体成像在望远镜的物镜像平面上,像平面的位置上安装了绘制定位十字线的玻璃板,然后通过望远镜的光学轴线分别定位在被测量物体的两端,可以在游标卡尺上读出测量点对应的坐标值,计算出物体的长度和高度.因为能够实现垂直方向的高度测量,所以命名为测高仪.其优点是测量时不需要直接接触被测量物体即可实现长度测量,因此作为一种长度测量的方法用于实验教学;其缺点是立柱量程有限,望远镜偏离水平方向的角度十分微小并且没有读数功能,因此高度测量的范围十分有限,主要用于测量工件的高度值.
2.2 791型测高仪的改进
图3为安装在垂直立柱上的环形滑块的原装望远镜安装结构简图,其立柱上标有长度刻度,垂直滑块上安装有游标,望远镜安装在滑块上的定位基座上,其中两个微调旋钮用于调节望远镜的水平状态.在这种结构中,望远镜只能够进行水平方向的测量.

图3 原装望远镜安装结构简图 图4 改装的望远镜安装结构简图
本文设计了一个新的望远镜调节机构,改装的望远镜安装结构简图如图4所示.
首先在定位基座上加装了一个横梁,在横梁上安装一个精密角度测量仪,选用的典型器材为一款分光计的测角度盘和游标盘,其测量的最小分度为2′,测角仪的定位轴线垂直于立柱轴线与原望远镜的水平光轴.其次,在游标盘上加装一套实现角度微调的齿轮调节机构,然后将望远镜固定在测角仪的游标盘上,安装时将二者的轴线调节为互相垂直状态.为了提高测量精度,将原来的望远镜更换为一个口径更大、具有内部调节透镜的、成像像距保持不变的望远镜.改装仪器的水平定位精度取决于望远镜初始水平角度的安装定位.改装后的望远镜可以实现水平方向360°、垂直方向仰角0°≤θ≤43°、俯角0°≤θ≤28°的角度测量,水平滑块移动范围15.00 cm,垂直滑块移动范围28.00 cm.
2.3 改进型测高仪的工作原理
改进型测高仪可以有两种测量方案,分别定义为基本测量方案和立柱测量方案.基本测量方案的原理如图5所示,图5中BC为被测量的建筑物,A点为望远镜初始定位点,B、C点为被测点,SAO为两点间的水平距离.如果用望远镜测量出B点和C点的竖直角θ1和θ2,再测量出SAO,则hBC=SAO(tanθ1+tanθ2),这就是经纬仪三角高程法的测量原理[1].如果将望远镜在A点测量出竖直角θ1和θ2后,再利用测高仪的水平滑块将望远镜向测量方向后方移动一段距离d,到达测量点A1,第二次测量B点的竖直角θ3,则有:
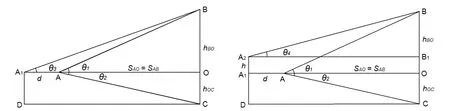
图5 基本测量方案 图6 立柱测量方案
(2)
(3)
当hBO保持不变,SAO超过一定距离时,竖直角θ1和θ2有可能十分接近,因为正切函数为非线性函数,微小测量误差会引起测量结果的很大误差,这时可以采用立柱测量方案测量.如图6所示,测角望远镜定位于A点时,使其水平滑块定位在测高仪的最前端,立柱滑块定位在立柱最低端,测量竖直角θ1和θ2;然后利用测高仪的水平滑块将望远镜向测量方向后方移动一段距离d,到达测量点A1,将立柱滑块抬升一段距离h,到达测量点A2,第二次测量B点的竖直角θ4,主动增加θ1与θ4的差值,则有:
(4)
(5)
测量仪器的精度标准差:σθ=2′=6×10-4rad,σd=σh=0.05 mm.不考虑地球半径等其他因素的影响,根据实验误差的基本理论[4],在基本测量方案和立柱测量方案中,测量结果SAO的理论标准差σSAO分别由公式(6)、(7)计算,σhBC可统一由公式(8)计算,公式中如果θ2=0,即是以A为基点的大地高程测量.
(6)
(7)
(8)
3 实验数据和误差分析
3.1 仪器功能鉴定测量数据
为了鉴定仪器工作方案的可行性,实验中将一个垂直悬挂的钢卷尺作为被测量标尺,设其刻度标准差为零,在一定距离以外进行测量,观察测量数据与标尺数据的吻合程度.表1、表2为基本测量方案、立柱测量方案鉴定数据单次测量的结果及误差分析,分别在两个位置各测量一组数据.测量过程中水平滑块移动距离d=15.000 cm,垂直滑块移动距离h=25.000 cm,Δ为实测值与标尺值的差值,σ为理论误差,单位为cm.
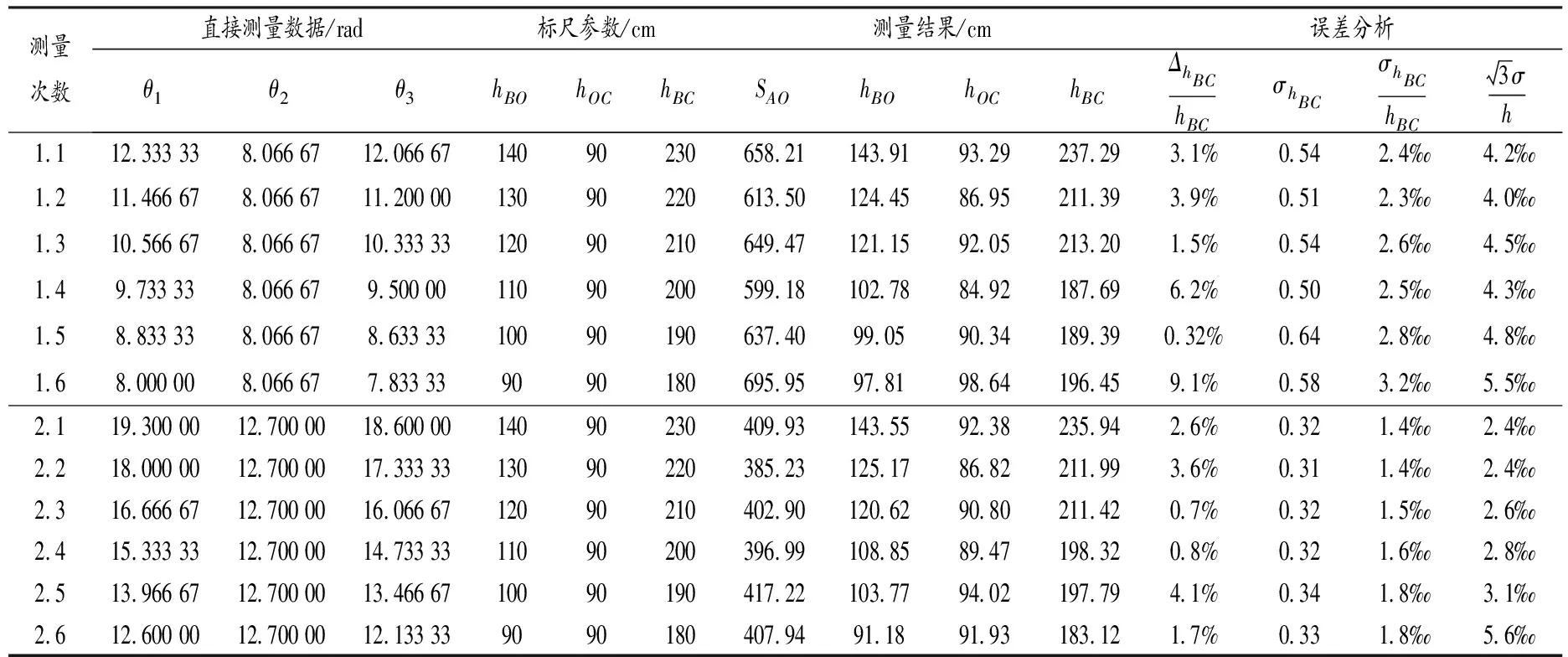
表1 基本测量方案鉴定数据单次测量结果
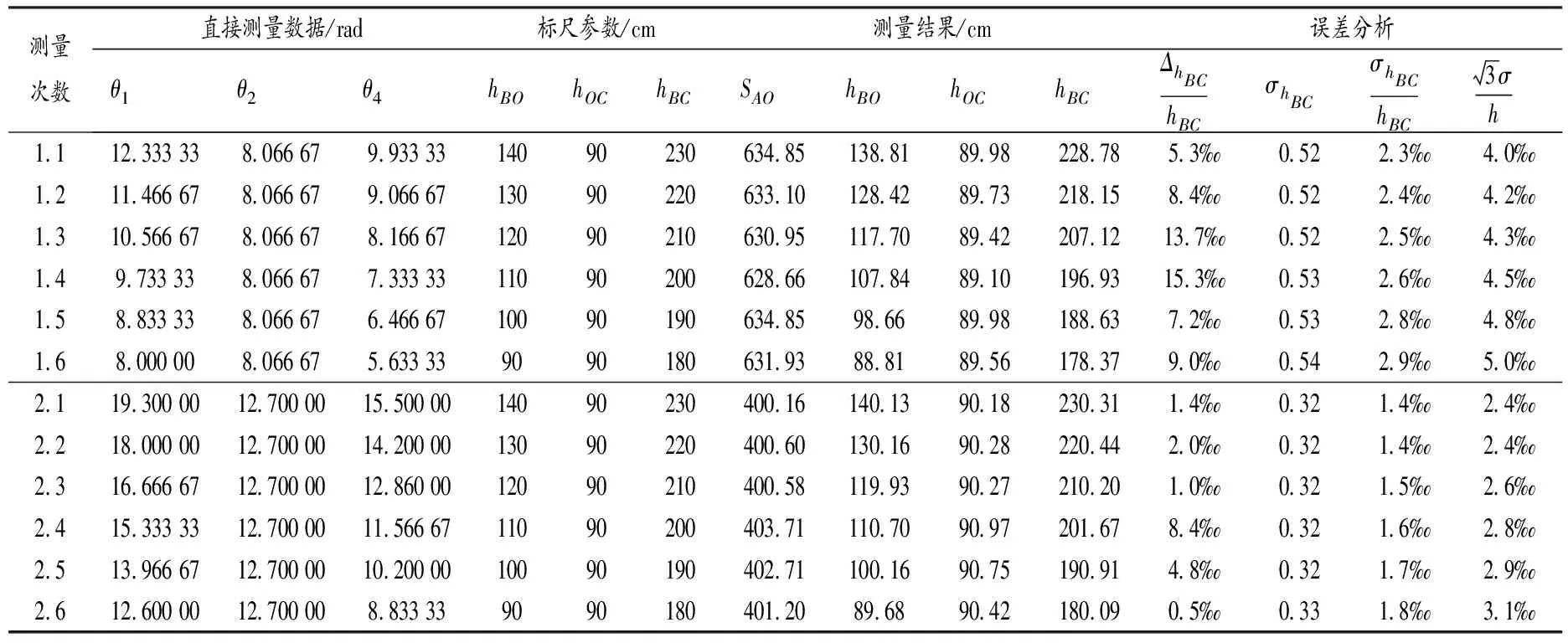
表2 立柱测量方案鉴定数据单次测量结果

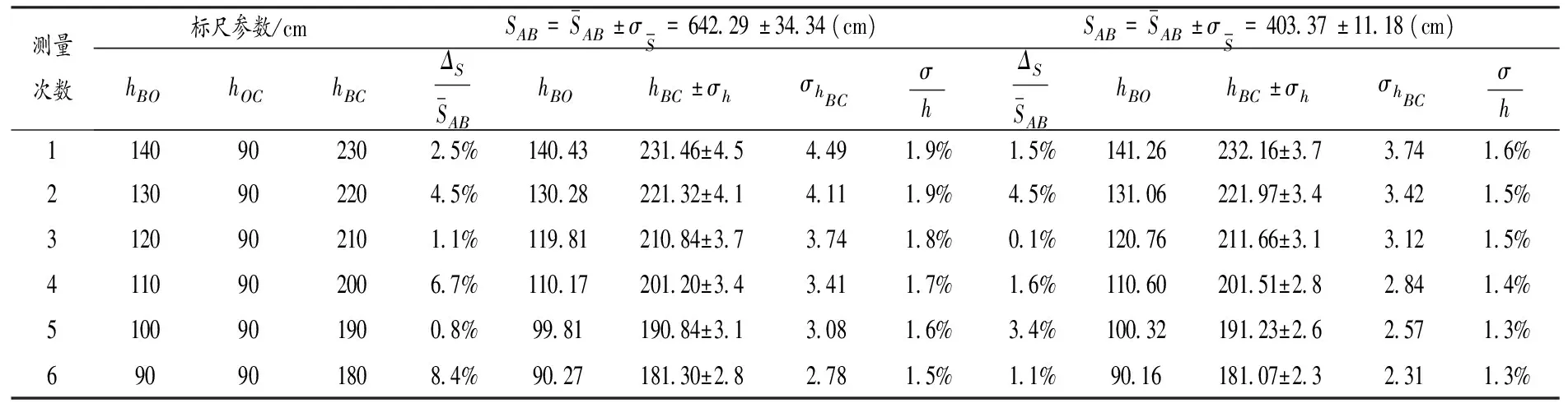
表3 基本测量方案鉴定数据多次测量结果
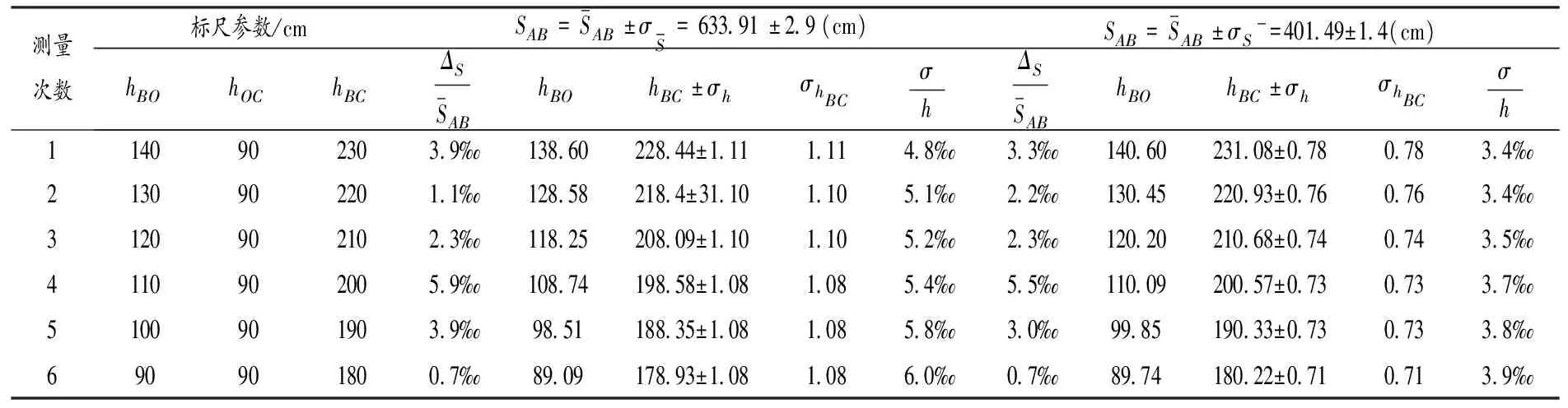
表4 立柱测量方案鉴定数据多次测量结果
3.2 实际应用测量数据
表5为利用仪器进行实际应用测量的数据.测量过程采用立柱测量方案,数据为对同一目标进行多次测量取得的平均值结果.测量过程中水平滑块移动距离d=15.000 cm,垂直滑块移动距离h=28.000 cm.仪器测量的平均值误差基本在1.6%附近,极限误差不超过2.77%,在实验室教学应用中完全可行.

表5 实际建筑物高度测量数据
4 小结
本文设计的在普通测高仪上加装精密测角仪的仪器结构,通过在同一个测量点短距离改变测量竖直角的望远镜位置定位,分别测量两次被测点的竖直角,可以不必直接测量水平距离而实现高度的间接测量,增加了一种高度测量方法,拓宽了物理实验教学内容.如果适当调整结构参数、改进望远镜的测量参数,提高测角仪的测量精度、仪器的制作安装精度,这一方案具有一定的实际应用性.
