初中生数学逻辑推理素养的调查与分析

于文波,孙 锐

(鞍山师范学院 数学与信息科学学院，辽宁 鞍山 114007)

《普通高中数学课程标准》指出，数学学科核心素养是数学课程目标的集中体现，是具有数学基本特征的思维品质、关键能力以及情感、态度与价值观的综合体现[1].逻辑推理在中学数学课程中一直处于十分重要的地位[2].如今，逻辑推理素养作为数学学科核心素养之一，更被赋予了新的内涵和意义.中学阶段是培养学生逻辑推理素养的关键时期，良好的逻辑推理素养可以帮助学生更好地提升自身的能力，并且随着知识水平的增长，学生也需要加强对外界事物的判断，以及在某些问题上的推理能力.逻辑推理素养在初中的代数与几何部分均有重要体现，尤其是在复杂的几何证明过程中.本文针对学生在学习特殊平行四边形中的逻辑推理素养水平进行调查研究，并给出有效的教学建议.

1 测试卷编写

测试卷以逻辑推理的概念、分类为理论基础，结合特殊的平行四边形知识内容，选取鞍山市某中学八年级学生213个测试样本，运用SPSS 21.0统计软件进行分析[3].

测试卷设置15道测试题(共60分)，包括合情推理试题和演绎推理试题.合情推理试题分为类比推理试题和归纳推理试题；演绎推理试题分为假言推理试题、选言推理试题和三段论试题，表1对于题目的分配进行了说明.测试内容选取特殊的平行四边形，包含矩形、菱形、正方形等.

表1 测试题分类表

2 数据处理

2.1 测试卷质量分析

2.1.1 信度分析 信度是数据的可靠程度，大多用内部一致性表示所测试卷信度的高低，信度系数越高表示结果越一致可靠.根据计算，可靠性统计量Cronbach’s Alpha系数为0.841(表2)，大于0.8，信度良好，测试结果可以采用.

表2 可靠性统计量

2.1.2 效度分析 效度是指检验测试结果能否反映初中生逻辑推理素养水平的指标.本测试对成绩进行降维因子分析，通过检验得到KMO>0.6可行，显著性水平sig.<0.01，为极显著(表3).所以，本测试题能够反映初中生在特殊平行四边形学习中的逻辑推理水平.

表3 KMO和Bartlett的检验

2.2 调查数据分析

2.2.1 描述性统计分析 根据表4可以发现，样本的标准误在合适范围内，试卷平均分为29.93，说明学生在特殊平行四边形方面的逻辑推理素养水平还有待提高.

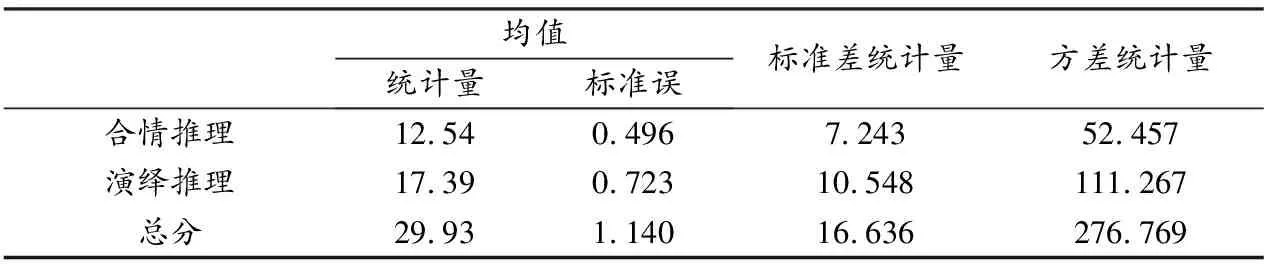
表4 描述性统计量表

根据图1可知，学生的逻辑推理水平呈现分化，高分段和低分段人数均多，而中分段的人数相对较少，说明学生的逻辑推理素养整体上还需要提高.

图1 学生得分分布直方图

针对总分进行正态Q-Q图分析，由图2的散点基本上呈现直线状可知，实际的数据和正态的期望相符合，数据的偏离情况处于对称性，大体上服从正态分布.结合图2与图3，可知学生得分在20分和40分上偏离严重，原因是学生对某类推理的掌握存在问题，不完全符合正态分布.

2.2.2 正态分析 由表5可知，学生在各推理上的得分情况大致在6分，其中，假言推理和选言推理相对于其他推理来说得分偏低，表明学生演绎推理水平有待提高.因此，对于演绎推理的各类推理要进行具体分析.

表5 学生各类推理得分情况

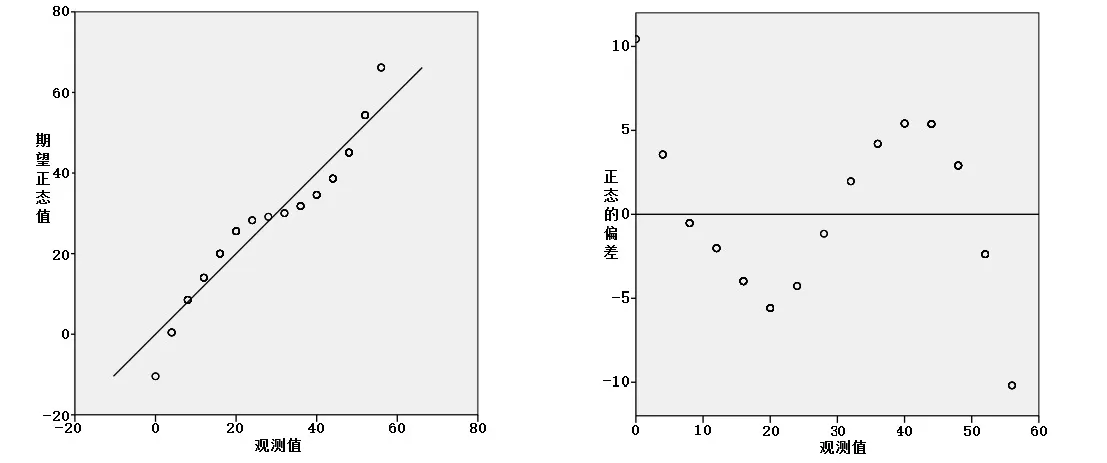
图2 总分的正态Q-Q图 图3 总分的趋降正态Q-Q图

据统计，假言推理部分的测试学生得12分的人数占18.8%，得分在0分和8分的人数分别占28.6%和28.2%，得4分的人数占24.4%，而且假言推理的分布不完全是正态分布.得分在8分以上的人数占总人数的47.0%，没有超过50%，说明学生在假言推理的学习上有很大的问题.综上，学生对假言推理的掌握不是很好，需要进一步加强.

选言推理部分的测试学生得分为0分、4分和8分的人数逐渐增多，分别为23.9%、27.7%和30.6%；得分为12分的人数占17.8%.得8分以上的人数(含8分)占总人数的48.4%，没有超过50%，但是得0分的人数比起假言推理得0分的人数少了一些.综上，学生对选言推理方面的掌握略好于假言推理.

三段论部分的测试学生得0分的人数占19.7%；得4分和8分的人数分别占27.7%和30.1%；得12分的人数占22.5%，和选言推理的人数分布近似.数据的大体走向同选言推理，说明学生在三段论部分的掌握情况同选言推理近似，也有进步的空间.得8分以上的人数(含8分)占总人数的52.6%，而且得0分的人数相比之前两类推理有明显减少，说明学生在三段论方面的掌握情况良好.

归纳推理部分的测试学生得0分、4分和12分的人数分别占22.1%、23.9%和23.0%；得8分的人数最多，占31%.得8分以上的人数(含8分)占总人数的54%，说明学生对归纳推理掌握良好.

类比推理部分的测试学生得0分的人数占18.8%，得4分的人数占26.3%，得8分的人数占32.4%，得12分的人数占22.5%.得8分以上的人数(含8分)占总人数的54.9%，说明学生对类比推理掌握良好.

通过对各类推理的测试得分分析，发现学生对选言推理和假言推理的掌握不好，而对三段论、归纳推理和类比推理的掌握较优于前两者.对假言推理的掌握尤其要引起注意，学生在假言推理素养方面明显出现了问题.同时，也要注意其他推理素养的发展情况，学生在每个推理上都存在较大的发展空间.

2.2.3 相关性分析 对于几种推理进行相关性分析，可以了解到不同推理之间的关系.一般来说，Pearson相关系数的判别标准是当相关系数在0.4～0.6时，两者存在中等程度相关性.

根据表6可知，几种推理素养存在中等程度的正相关性，显著性P值为0.000<0.050，说明其存在显著性相关.因此，可以得出学生对于几种推理的掌握情况具有一致性的结论.

表6 相关性分析表

3 课堂教学中培养中学生逻辑推理素养的建议

以菱形的定义和性质教学为例，结合实际调查和数据分析，给出以下教学建议：

(1)课程引入环节可以应用合情推理.引导学生联系以往学习的旧知识，思考探究本节课所要学习的新内容，类比平行四边形以及矩形的定义、性质的学习过程来探究菱形的相应知识.

(2)探究新知过程可以通过学生的动手操作去猜想、发现，由学生自己运用归纳推理方法，对菱形的定义、性质等进行归纳.

(3)菱形性质证明、面积公式的推导和课堂练习阶段融入演绎推理，尽可能将假言推理、选言推理和三段论设置在例题或者练习题目中.教师尤其要注重学生在应用演绎推理环节的表现情况.

总之，在本节课的课堂教学中，教师将逻辑推理贯穿于整个教学过程，让学生在学会知识的同时不断提高数学逻辑推理素养，有助于学生在以后的学习中独立解决类似问题，实现学生在数学素养上的全面提高.教师要注重概念、性质的教学，并要及时强化，可以通过图示或者表格等手段直观地表示平行四边形和特殊的平行四边形之间的关系，引导学生构建自己的知识体系；促使学生提出问题，并运用合情推理得到结论，再运用演绎推理证明这个结论的正确性[4].在此过程中，也要重视逻辑推理素养和其他素养之间的联系.

在培养学生逻辑推理素养过程中，不能墨守成规、一成不变，要具体情况具体分析.同时，教师也要加强学生逻辑推理素养水平的检验，检验结果有助于教师及时调整教学方法，进而帮助学生提升逻辑推理素养水平.

4 结论

研究表明，该校八年级学生的逻辑推理素养处于中等水平.学生在假言推理方面的素养明显薄弱，在合情推理方面的素养优于演绎推理.教师要注重学生假言推理和选言推理素养的培养，并且注意各类推理之间的相关性.教师在教学中要加强对学生逻辑推理的培养，根据教学内容进行合理的教学设计，使学生逻辑推理素养水平得到提高.